人教版(2023春)数学五年级下册6.2.3 图形的认识与测量(三)(教材P87页例4、例5)课件(52张PPT)
文档属性
| 名称 | 人教版(2023春)数学五年级下册6.2.3 图形的认识与测量(三)(教材P87页例4、例5)课件(52张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 00:00:00 | ||
图片预览




文档简介
(共52张PPT)
人教版数学六年级下册
3.图形的认识与测量(三)
(教材P87例4、例5)
第六单元 整理和复习
复习导入
1、请同学们回忆一下,我们学过哪些立体图形,它 们都有什么特征?
长方体,正方体,圆柱、圆锥。
2、你能不能将这些立体图形进行分类?
分类1:长方体和正方体是一类,它们每个面都是平面;圆柱和圆锥
是一类,它们有一个面是曲面。
分类2:长方体、正方体和圆柱是一类,因为它们上下一样粗细;圆
锥是一类。
复习导入
3、请同学们说一下什么是体积单位,你学过哪些体积单位?
4、什么是容积?你学过哪些容积单位?说一说容积与体积的区别和联系。
体积是物件占有多少空间的量。体积的国际单位制是立方米。常用的体积单位有:(立方米)、d (立方分米)、 立方厘米等。
容积是指箱子、油桶、仓库等所能容纳物体的体积。通常叫做它们的容积。计量容积,一般就用体积单位。计量液体的体积,如水,油等,常用容积单位升和毫升,也可以写成L和mL。
1、含义不同。如一只铁桶的体积是指它外部所占空间部分的大小,而这只铁桶的容积却是指它内部容纳物体的多少。一种物体有体积,可不一定有容积。
2、测量方法不同。在计算物体的体积或容积前一般要先测量长、宽、高,求物体的体积是从该物体的外部来测量,而求容积却是从物体的内部来测量。一种既有体积又有容积的封闭物体,它的体积一定大于它的容积。
3、单位名称不完全相同。体积单位一般用:立方米、立方分米、立方厘米;固体的容积单位与体积单位相同,而液体和气体的体积与容积单位一般都用升、毫升。
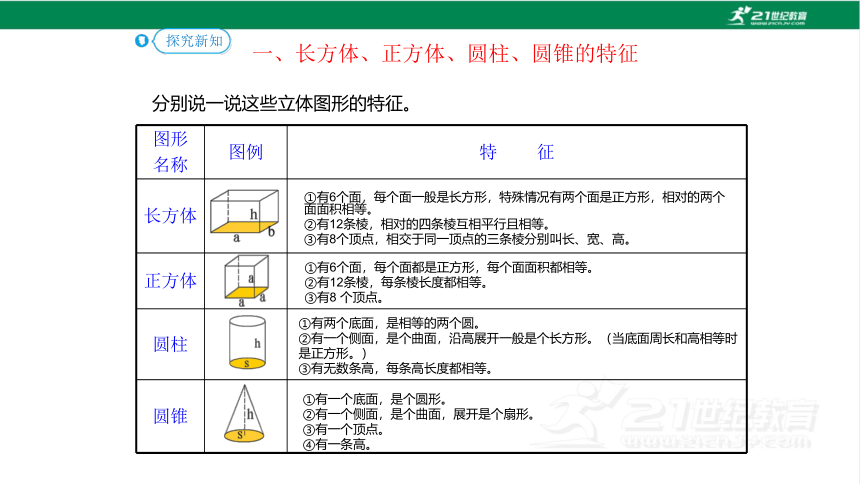
一、长方体、正方体、圆柱、圆锥的特征
图形 名称 图例 特 征
长方体
正方体
圆柱
圆锥
①有6个面,每个面一般是长方形,特殊情况有两个面是正方形,相对的两个面面积相等。
②有12条棱,相对的四条棱互相平行且相等。
③有8个顶点,相交于同一顶点的三条棱分别叫长、宽、高。
①有6个面,每个面都是正方形,每个面面积都相等。
②有12条棱,每条棱长度都相等。
③有8 个顶点。
①有两个底面,是相等的两个圆。
②有一个侧面,是个曲面,沿高展开一般是个长方形。(当底面周长和高相等时是正方形。)
③有无数条高,每条高长度都相等。
①有一个底面,是个圆形。
②有一个侧面,是个曲面,展开是个扇形。
③有一个顶点。
④有一条高。
探究新知
分别说一说这些立体图形的特征。
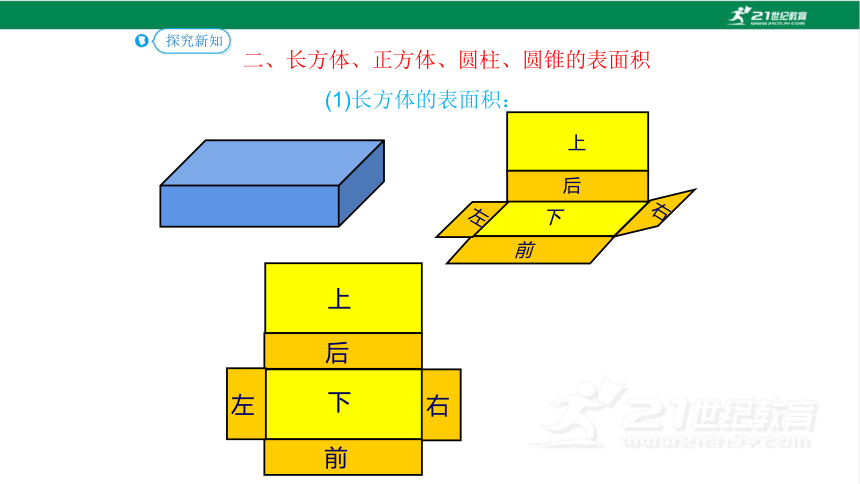
(1)长方体的表面积:
二、长方体、正方体、圆柱、圆锥的表面积
探究新知
上
下
前
后
左
右
上
下
前
后
左
右
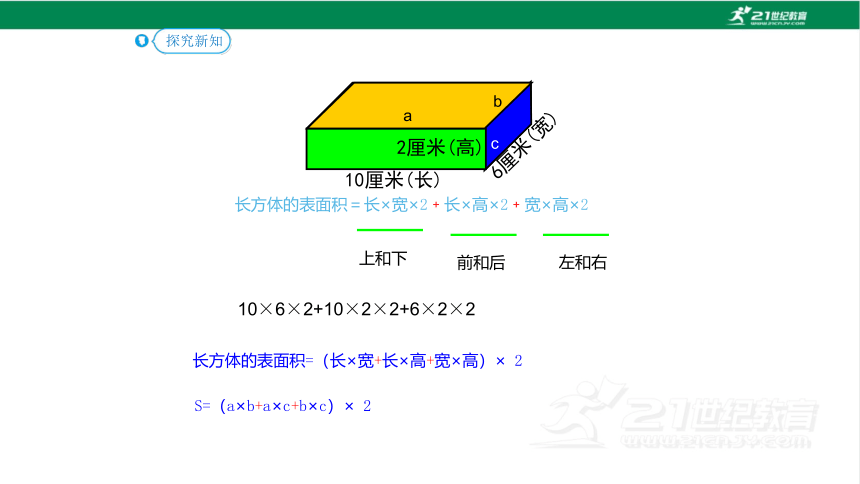
10厘米(长)
6厘米(宽)
2厘米(高)
10×6×2+10×2×2+6×2×2
上和下
前和后
左和右
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
长方体的表面积=(长×宽+长×高+宽×高)× 2
探究新知
S=(a×b+a×c+b×c)× 2
a
b
c
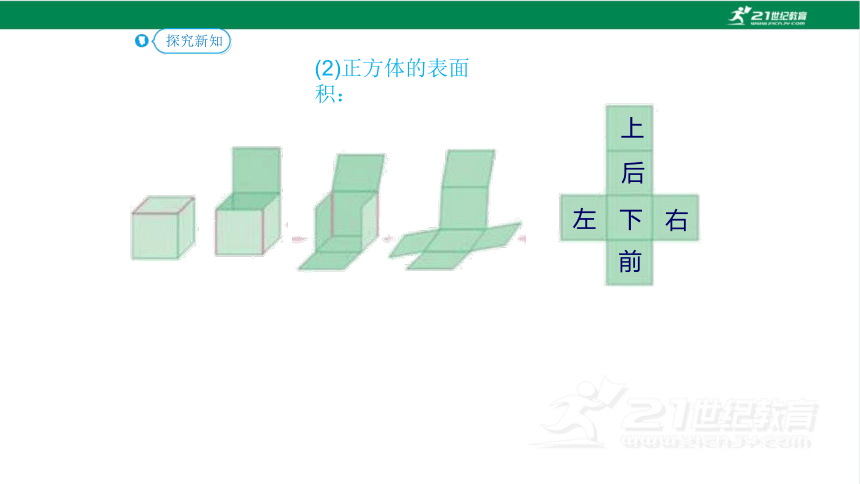
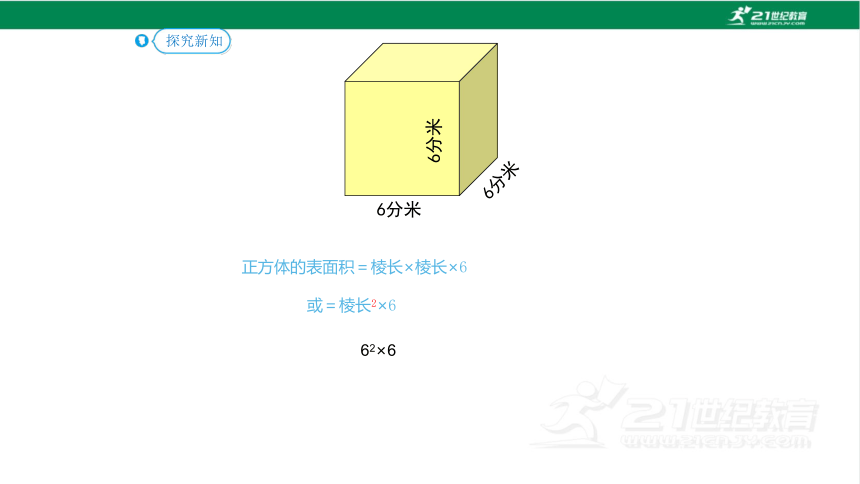
(2)正方体的表面积:
探究新知
上
下
前
后
左
右
正方体的表面积=棱长×棱长×6
或=棱长2×6
6分米
6分米
6分米
62×6
探究新知
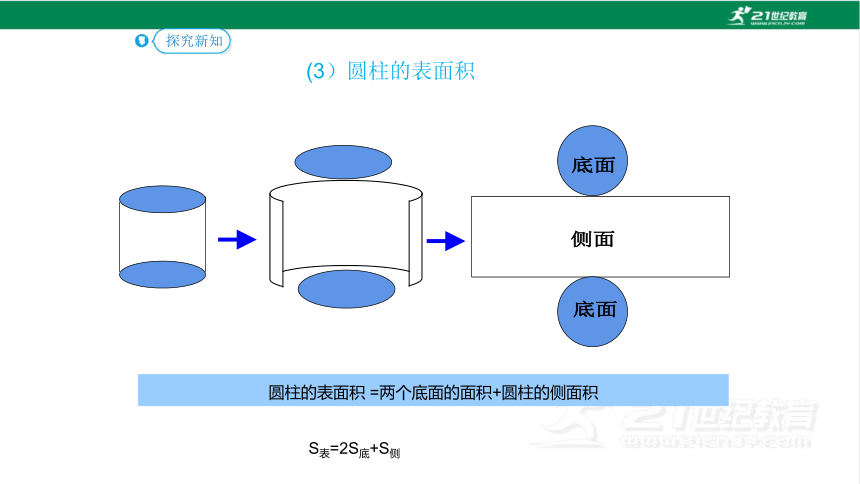
底面
底面
侧面
圆柱的表面积 =两个底面的面积+圆柱的侧面积
S表=2S底+S侧
(3)圆柱的表面积
探究新知
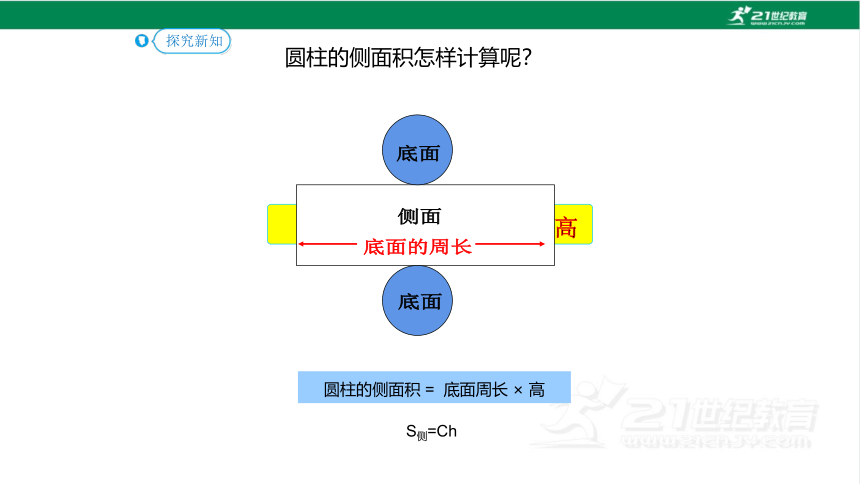
圆柱的侧面积怎样计算呢?
底面
底面
底面的周长
高
侧面
圆柱的侧面积 = 底面周长 × 高
S侧=Ch
探究新知
长5厘米
宽4厘米
高3厘米
请大家回忆一下长方体的体积计算方法。
长方体的体积=长×宽×高
V=abh
长方体的体积=底面积×高
(1)长方体的体积:
三、长方体、正方体、圆柱、圆锥的体积
探究新知
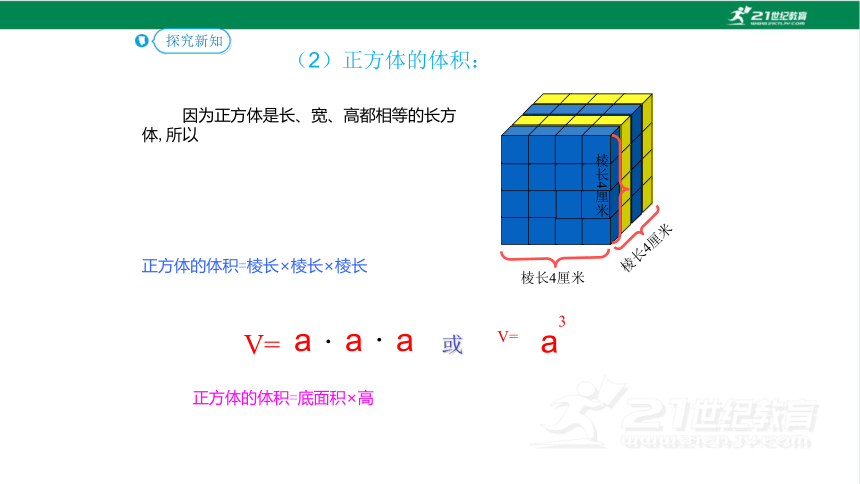
棱长4厘米
棱长4厘米
棱长4厘米
因为正方体是长、宽、高都相等的长方体,所以
正方体的体积=棱长×棱长×棱长
V=
a
a
a
V=
3
a
或
正方体的体积=底面积×高
(2)正方体的体积:
探究新知
·
·
长方体体积=底面积×高
圆柱体积
V=Sh
(3)圆柱的体积:
探究新知
底面积相等
高相等
=
还记得我们用什么方法计算出圆锥体积的吗?
因为 V圆柱=Sh
(4)圆锥的体积:
探究新知
长方体、正方体、圆柱、圆锥表面积、体积计算比较
图形 名称 图例 棱长总和 表面积 体积 长方体
正方体 圆柱 圆锥 4a+4b+4h
或4(a+b+h)
S长=2ab+2ah+2bh
=(ab+ah+bh)×2
S正=a2×6
S表=2S底+S侧
S侧=Ch
V长=abh
12a
V正=a3
V柱=Sh
V=Sh
探究新知
表面积成n2 倍增长。体积成n3倍增长。
观察并完成下表,你会发现什么?
22
6
88
48
352
384
我发现了:长方体的长、宽、高都变为原来的n倍,它的表面积跟着变为原来的n2倍,体积也跟着变为原来的n3倍。
探究新知
长高宽成倍增长
盒子的体积与盒子的容积哪个大 ?
仔细观察:
对于同一个容器,它的体积一定比容积大,因为它有厚度。
容器的容积计算方法同体积的计算方法一样,但是要从容器的里面量数据。
四、物体的容积
探究新知
表面积 体积 容积
意义
常用计量单位
单位间进率
物体表面面积的总和(所有面面积的总和)
物体所占空间的大小
容器所能容纳物体体积的大小
m dm cm
m dm cm
m dm cm
L ml
1m =100dm
1dm =100cm
1m =1000dm
1dm =1000cm
1L=1000ml
1dm =1L
1cm =1ml
五、表面积、体积、容积的对比
探究新知
完成下表,说一说表面积、体积和容积的区别
1、长方体、正方体、圆柱的体积都可以用底面积乘高来计算。( )
2、圆锥的体积是圆柱体积的 。( )
3、一个圆柱形杯子的体积等于它的容积。( )
4、一个圆柱的高缩小2倍,底面半径扩大2 倍,它的体积不变。( )
5、圆柱的底面直径和高相等,那么它的侧面展开是一个正方形。( )
√
×
一、 判断:
×
×
×
基础练习
6、计算圆柱形油桶能装多少升油就是求这个油桶的容积。( )
7、圆柱底面直径扩大2倍,高不变,它的体积也扩大2倍。( )
8、圆柱的底面周长和高相等时,它的侧面展开图一定是正方形。( )
9、求做一个圆柱形的通风管需要多少铁皮,就是求圆柱的表面积。( )
√
×
√
×
基础练习
14、两个大小相等的正方体合在一起,成了一个长方体,那么它就有12个面。( )
12、如果一个长方体的12条棱都相等,这个长方体就是正方体。( )
10、正方体6个面的形状相同、大小相等。( )
11、有6个面、12条棱、8个顶点的图形一定是长方体。 ( )
13、一个长方体的所有面都是长方形。( )
√
×
×
×
√
基础练习
15、长方体和正方体都有6个面,12条棱,8个顶点。 ( )
16、正方体的六个面面积一定相等。( ) 17、一个长方体(非正方体)最多有四个面面积相等。( )
18、一个木箱的体积就是它的容积。( )
19、长方体是特殊的正方体。( )
20、棱长6分米的正方体,它的表面积和体积相等。( )
21、用4个棱长1厘米的小正方体可以拼成一个大正方体。( )
√
√
√
×
×
×
×
基础练习
22、相交于一个顶点的三条棱相等的长方体一定是正方体。( )
23、 长方体有6个面,每个面有4条棱,共24条棱。( ) 24、正方体是一种特殊的长方体。( )
25、圆柱的侧面展开一定是长方形。( )
26、一根长24厘米的铁丝制作成一个正方体框架,棱长是3厘米。( )
√
×
√
×
×
基础练习
27、体积单位间的进率都是1000 。 ( )
28、把一个正方体的橡皮泥捏成一个长方体后虽然它的形状变了,但是它所占的空间大小不变。( )
29、正方体的棱长扩大2倍,它的体积就扩大6倍。( )
30、冰箱的容积就是冰箱的体积。( )
31、一个薄塑料长方体(厚度不计),它的体积就是容积。( )
32、一个油桶能装多少升油,就是求它的容积。( )
×
√
×
×
√
√
基础练习
1、把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体。下面哪句话是正确的?( )
A、表面积和体积都没变化。
B、表面积和体积都发生了变化。
C、表面积变了,体积没变。
D、表面积没变,体积变了。
C
二、选择:
基础练习
A、54 B、18 C 、0.6 D、6
2、等底等体积的圆柱和圆锥,圆锥的高是18厘米,那么圆柱的高是( )厘米。
D
基础练习
3、等高等体积的圆柱和圆锥,圆柱的底面积是6平方厘米,那么圆锥的底面积是( )平方厘米。
A、6 B、18 C、2 D、36
B
基础练习
4、把一个底面半径是2分米、高是3分米的圆柱形容器中注满水,现垂直轻轻插入一根底面积是5平方分米,高是4分米的方钢,溢出水的体积是( )毫升。
A、20 B、15 C、20000 D、15000
D
基础练习
1.一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
2×3.14×10
3.14×102
3.14×102+2×3.14×10×20
3.14×102×20
基础练习
三、回答下面的问题,并列出算式(不计算):
求底面周长
求底面积
求表面积
求容积
2、做一个圆柱形的油箱,底面半径3分米,高4分米。至少需要铁皮多少平方分米?
3、做一个无盖的圆柱形的水桶,底面直径6分米,高4分米。至少需要铁皮多少平方分米?
4、做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?
18.84 × 4
3.14 ×32×2 + 2×3.14×3×4
3.14×(6÷2)2 + 3.14×6×4
基础练习
1、一个鱼塘长8m,宽4.5m,深2m,这个鱼塘的容积是多少立方米?
8×4.5×2
=36×2
=72(m3)
答:这个鱼塘的容积是72m3。
基础练习
2、新建的篮球馆要铺设3cm厚的木质地板,已知该馆长36m,宽20m,铺设它至少需要用多少立方米木材?
3cm=0.03m
36×20×0.03
=720×0.03
=21.6(m3)
答:铺设它至少需要用21.6m3木材。
四、解决问题
3、把两个棱长是4厘米的正方体木块粘合成一个长方体,这个长方体的表面积是多少平方厘米?
方法三、4×4×10=160(平方厘米)
方法一、(8×4+8×4+4×4)×2=160(平方厘米)
方法四、4×4×12- 4×4×2=160(平方厘米)
方法二、8×4×4 + 4×4×2=160(平方厘米)
基础练习
四、解决问题
4、用铁丝做一个长10厘米,宽5厘米,高4厘米的长方体框架,至少需要多长的铁丝?在这个长方体框架外面糊一层纸,至少需要多少平方厘米的纸?
10
5
4
(1)求至少需要多长的铁丝 (10+5+4)×4=76 (厘米)
(2)求至少需要多少平方厘米的纸 (10×5+10×4+5×4)×2=220(平方厘米)
基础练习
四、解决问题
1、圆柱长10厘米,接上4厘米的一段后,表面积增加了25.12平方厘米,原来圆柱的体积是多少立方厘米?
25.12÷4÷3.14÷2
(1)求底面半径:
=6.28÷3.14÷2
=1(cm)
(2)求原来的圆柱体积:
3.14×12×10
=31.4(cm3)
答:原来圆柱的体积是31.4cm3。
拓展练习
2、把一根长30厘米的长方体木料锯成3段(如图),表面积比原来增加了20平方厘米,这根木料原来的体积是多少立方厘米
20÷4=5(平方厘米)
30×5=150(立方厘米)
答:这根木料原来的体积是150立方厘米。
拓展练习
3、一个底面是正方形的长方体,把它的侧面展开后得到一个边长是12厘米的正方形。这个长方体的体积是多少?
12
12
12
3
3
12÷4=3(厘米)
3×3×12=108(立方厘米)
答:这个长方体的体积是108立方厘米。
拓展练习
4、一个圆柱形木材,沿着一条底面直径纵向剖开,量得一个纵剖面面积是6平方分米,那么,圆柱的侧面积是多少平方分米
3.14×6=18.84(平方分米)
拓展练习
纵剖面面积=dh
圆柱侧面积=πdh
5、将一个圆柱沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米
拓展练习
(1)增加的面积是什么部分?
增加的面积是2个切开的纵剖面。
(2)切开的一个纵剖面面积是怎么计算出来的?
底面直径×高
(3)圆柱的高你能算出来吗?
20÷4=5(厘米)
(4)圆柱的体积你能算出来吗?
π×5=62.8()
(1)把长、宽、高平均分成的份数:(5+4+3)×4=48
(5)纸的面积:(2.5×2+2.5×1.5+2×1.5)×2=23.5(dm2)
(6)体积:2.5×2×1.5=7.5(dm3)
6、用一根长24dm的铁丝做一个长方体框架,使它的长、宽、高的比为5:4:3。在这 个长方体框架外面糊一层纸,至少需要多少平方分米的纸?它的体积是多少立方分米?
拓展练习
拓展练习
7、
下面这些图形是从什么角度看到的?
从左面
从下面
从前面
拓展练习
8、
F
E
B的长和宽;A的宽。
(1)小正方体的个数:
63÷23=27(个)
(2)表面积增加了:
62×6-22×6=192(cm2)
9、把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体?表面积增加了多少?
拓展练习
(1)正方体体积: 103=1000(cm3)
(2)圆锥的底面积:3.14×(10÷2)2=78.5(cm2)
(3)圆锥的高:1000×3÷78.5≈38(cm)
10、把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块,这个圆锥形铁块的高约是多少?(得数保留整厘米数)
拓展练习
拓展练习
11
(1)工作1分钟前进了多少米其实是求什么?
求15 倍的前轮周长。
15×3.14×1=47.1(米)
(2)工作1分钟压过的路面面积是多少平方米其实是求什么?
求15 倍的侧面积。
15×3.14×1×1.2=56.52(平方米)
(1)表面积:
202×5+3.14×102+2×3.14×10×20÷2
=2000+314+628
=2942(cm2)
(2)体积:
203+3.14×102×20÷2
=8000+3140
=11140(cm3)
拓展练习
12.
(1)10个正方体。
(2)体积:53×10=1250(cm3)
(3)表面积:52×34=850(cm2)
13.
拓展练习
14.
拓展练习
拓展练习
15.
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版数学六年级下册
3.图形的认识与测量(三)
(教材P87例4、例5)
第六单元 整理和复习
复习导入
1、请同学们回忆一下,我们学过哪些立体图形,它 们都有什么特征?
长方体,正方体,圆柱、圆锥。
2、你能不能将这些立体图形进行分类?
分类1:长方体和正方体是一类,它们每个面都是平面;圆柱和圆锥
是一类,它们有一个面是曲面。
分类2:长方体、正方体和圆柱是一类,因为它们上下一样粗细;圆
锥是一类。
复习导入
3、请同学们说一下什么是体积单位,你学过哪些体积单位?
4、什么是容积?你学过哪些容积单位?说一说容积与体积的区别和联系。
体积是物件占有多少空间的量。体积的国际单位制是立方米。常用的体积单位有:(立方米)、d (立方分米)、 立方厘米等。
容积是指箱子、油桶、仓库等所能容纳物体的体积。通常叫做它们的容积。计量容积,一般就用体积单位。计量液体的体积,如水,油等,常用容积单位升和毫升,也可以写成L和mL。
1、含义不同。如一只铁桶的体积是指它外部所占空间部分的大小,而这只铁桶的容积却是指它内部容纳物体的多少。一种物体有体积,可不一定有容积。
2、测量方法不同。在计算物体的体积或容积前一般要先测量长、宽、高,求物体的体积是从该物体的外部来测量,而求容积却是从物体的内部来测量。一种既有体积又有容积的封闭物体,它的体积一定大于它的容积。
3、单位名称不完全相同。体积单位一般用:立方米、立方分米、立方厘米;固体的容积单位与体积单位相同,而液体和气体的体积与容积单位一般都用升、毫升。
一、长方体、正方体、圆柱、圆锥的特征
图形 名称 图例 特 征
长方体
正方体
圆柱
圆锥
①有6个面,每个面一般是长方形,特殊情况有两个面是正方形,相对的两个面面积相等。
②有12条棱,相对的四条棱互相平行且相等。
③有8个顶点,相交于同一顶点的三条棱分别叫长、宽、高。
①有6个面,每个面都是正方形,每个面面积都相等。
②有12条棱,每条棱长度都相等。
③有8 个顶点。
①有两个底面,是相等的两个圆。
②有一个侧面,是个曲面,沿高展开一般是个长方形。(当底面周长和高相等时是正方形。)
③有无数条高,每条高长度都相等。
①有一个底面,是个圆形。
②有一个侧面,是个曲面,展开是个扇形。
③有一个顶点。
④有一条高。
探究新知
分别说一说这些立体图形的特征。
(1)长方体的表面积:
二、长方体、正方体、圆柱、圆锥的表面积
探究新知
上
下
前
后
左
右
上
下
前
后
左
右
10厘米(长)
6厘米(宽)
2厘米(高)
10×6×2+10×2×2+6×2×2
上和下
前和后
左和右
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
长方体的表面积=(长×宽+长×高+宽×高)× 2
探究新知
S=(a×b+a×c+b×c)× 2
a
b
c
(2)正方体的表面积:
探究新知
上
下
前
后
左
右
正方体的表面积=棱长×棱长×6
或=棱长2×6
6分米
6分米
6分米
62×6
探究新知
底面
底面
侧面
圆柱的表面积 =两个底面的面积+圆柱的侧面积
S表=2S底+S侧
(3)圆柱的表面积
探究新知
圆柱的侧面积怎样计算呢?
底面
底面
底面的周长
高
侧面
圆柱的侧面积 = 底面周长 × 高
S侧=Ch
探究新知
长5厘米
宽4厘米
高3厘米
请大家回忆一下长方体的体积计算方法。
长方体的体积=长×宽×高
V=abh
长方体的体积=底面积×高
(1)长方体的体积:
三、长方体、正方体、圆柱、圆锥的体积
探究新知
棱长4厘米
棱长4厘米
棱长4厘米
因为正方体是长、宽、高都相等的长方体,所以
正方体的体积=棱长×棱长×棱长
V=
a
a
a
V=
3
a
或
正方体的体积=底面积×高
(2)正方体的体积:
探究新知
·
·
长方体体积=底面积×高
圆柱体积
V=Sh
(3)圆柱的体积:
探究新知
底面积相等
高相等
=
还记得我们用什么方法计算出圆锥体积的吗?
因为 V圆柱=Sh
(4)圆锥的体积:
探究新知
长方体、正方体、圆柱、圆锥表面积、体积计算比较
图形 名称 图例 棱长总和 表面积 体积 长方体
正方体 圆柱 圆锥 4a+4b+4h
或4(a+b+h)
S长=2ab+2ah+2bh
=(ab+ah+bh)×2
S正=a2×6
S表=2S底+S侧
S侧=Ch
V长=abh
12a
V正=a3
V柱=Sh
V=Sh
探究新知
表面积成n2 倍增长。体积成n3倍增长。
观察并完成下表,你会发现什么?
22
6
88
48
352
384
我发现了:长方体的长、宽、高都变为原来的n倍,它的表面积跟着变为原来的n2倍,体积也跟着变为原来的n3倍。
探究新知
长高宽成倍增长
盒子的体积与盒子的容积哪个大 ?
仔细观察:
对于同一个容器,它的体积一定比容积大,因为它有厚度。
容器的容积计算方法同体积的计算方法一样,但是要从容器的里面量数据。
四、物体的容积
探究新知
表面积 体积 容积
意义
常用计量单位
单位间进率
物体表面面积的总和(所有面面积的总和)
物体所占空间的大小
容器所能容纳物体体积的大小
m dm cm
m dm cm
m dm cm
L ml
1m =100dm
1dm =100cm
1m =1000dm
1dm =1000cm
1L=1000ml
1dm =1L
1cm =1ml
五、表面积、体积、容积的对比
探究新知
完成下表,说一说表面积、体积和容积的区别
1、长方体、正方体、圆柱的体积都可以用底面积乘高来计算。( )
2、圆锥的体积是圆柱体积的 。( )
3、一个圆柱形杯子的体积等于它的容积。( )
4、一个圆柱的高缩小2倍,底面半径扩大2 倍,它的体积不变。( )
5、圆柱的底面直径和高相等,那么它的侧面展开是一个正方形。( )
√
×
一、 判断:
×
×
×
基础练习
6、计算圆柱形油桶能装多少升油就是求这个油桶的容积。( )
7、圆柱底面直径扩大2倍,高不变,它的体积也扩大2倍。( )
8、圆柱的底面周长和高相等时,它的侧面展开图一定是正方形。( )
9、求做一个圆柱形的通风管需要多少铁皮,就是求圆柱的表面积。( )
√
×
√
×
基础练习
14、两个大小相等的正方体合在一起,成了一个长方体,那么它就有12个面。( )
12、如果一个长方体的12条棱都相等,这个长方体就是正方体。( )
10、正方体6个面的形状相同、大小相等。( )
11、有6个面、12条棱、8个顶点的图形一定是长方体。 ( )
13、一个长方体的所有面都是长方形。( )
√
×
×
×
√
基础练习
15、长方体和正方体都有6个面,12条棱,8个顶点。 ( )
16、正方体的六个面面积一定相等。( ) 17、一个长方体(非正方体)最多有四个面面积相等。( )
18、一个木箱的体积就是它的容积。( )
19、长方体是特殊的正方体。( )
20、棱长6分米的正方体,它的表面积和体积相等。( )
21、用4个棱长1厘米的小正方体可以拼成一个大正方体。( )
√
√
√
×
×
×
×
基础练习
22、相交于一个顶点的三条棱相等的长方体一定是正方体。( )
23、 长方体有6个面,每个面有4条棱,共24条棱。( ) 24、正方体是一种特殊的长方体。( )
25、圆柱的侧面展开一定是长方形。( )
26、一根长24厘米的铁丝制作成一个正方体框架,棱长是3厘米。( )
√
×
√
×
×
基础练习
27、体积单位间的进率都是1000 。 ( )
28、把一个正方体的橡皮泥捏成一个长方体后虽然它的形状变了,但是它所占的空间大小不变。( )
29、正方体的棱长扩大2倍,它的体积就扩大6倍。( )
30、冰箱的容积就是冰箱的体积。( )
31、一个薄塑料长方体(厚度不计),它的体积就是容积。( )
32、一个油桶能装多少升油,就是求它的容积。( )
×
√
×
×
√
√
基础练习
1、把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体。下面哪句话是正确的?( )
A、表面积和体积都没变化。
B、表面积和体积都发生了变化。
C、表面积变了,体积没变。
D、表面积没变,体积变了。
C
二、选择:
基础练习
A、54 B、18 C 、0.6 D、6
2、等底等体积的圆柱和圆锥,圆锥的高是18厘米,那么圆柱的高是( )厘米。
D
基础练习
3、等高等体积的圆柱和圆锥,圆柱的底面积是6平方厘米,那么圆锥的底面积是( )平方厘米。
A、6 B、18 C、2 D、36
B
基础练习
4、把一个底面半径是2分米、高是3分米的圆柱形容器中注满水,现垂直轻轻插入一根底面积是5平方分米,高是4分米的方钢,溢出水的体积是( )毫升。
A、20 B、15 C、20000 D、15000
D
基础练习
1.一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
2×3.14×10
3.14×102
3.14×102+2×3.14×10×20
3.14×102×20
基础练习
三、回答下面的问题,并列出算式(不计算):
求底面周长
求底面积
求表面积
求容积
2、做一个圆柱形的油箱,底面半径3分米,高4分米。至少需要铁皮多少平方分米?
3、做一个无盖的圆柱形的水桶,底面直径6分米,高4分米。至少需要铁皮多少平方分米?
4、做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?
18.84 × 4
3.14 ×32×2 + 2×3.14×3×4
3.14×(6÷2)2 + 3.14×6×4
基础练习
1、一个鱼塘长8m,宽4.5m,深2m,这个鱼塘的容积是多少立方米?
8×4.5×2
=36×2
=72(m3)
答:这个鱼塘的容积是72m3。
基础练习
2、新建的篮球馆要铺设3cm厚的木质地板,已知该馆长36m,宽20m,铺设它至少需要用多少立方米木材?
3cm=0.03m
36×20×0.03
=720×0.03
=21.6(m3)
答:铺设它至少需要用21.6m3木材。
四、解决问题
3、把两个棱长是4厘米的正方体木块粘合成一个长方体,这个长方体的表面积是多少平方厘米?
方法三、4×4×10=160(平方厘米)
方法一、(8×4+8×4+4×4)×2=160(平方厘米)
方法四、4×4×12- 4×4×2=160(平方厘米)
方法二、8×4×4 + 4×4×2=160(平方厘米)
基础练习
四、解决问题
4、用铁丝做一个长10厘米,宽5厘米,高4厘米的长方体框架,至少需要多长的铁丝?在这个长方体框架外面糊一层纸,至少需要多少平方厘米的纸?
10
5
4
(1)求至少需要多长的铁丝 (10+5+4)×4=76 (厘米)
(2)求至少需要多少平方厘米的纸 (10×5+10×4+5×4)×2=220(平方厘米)
基础练习
四、解决问题
1、圆柱长10厘米,接上4厘米的一段后,表面积增加了25.12平方厘米,原来圆柱的体积是多少立方厘米?
25.12÷4÷3.14÷2
(1)求底面半径:
=6.28÷3.14÷2
=1(cm)
(2)求原来的圆柱体积:
3.14×12×10
=31.4(cm3)
答:原来圆柱的体积是31.4cm3。
拓展练习
2、把一根长30厘米的长方体木料锯成3段(如图),表面积比原来增加了20平方厘米,这根木料原来的体积是多少立方厘米
20÷4=5(平方厘米)
30×5=150(立方厘米)
答:这根木料原来的体积是150立方厘米。
拓展练习
3、一个底面是正方形的长方体,把它的侧面展开后得到一个边长是12厘米的正方形。这个长方体的体积是多少?
12
12
12
3
3
12÷4=3(厘米)
3×3×12=108(立方厘米)
答:这个长方体的体积是108立方厘米。
拓展练习
4、一个圆柱形木材,沿着一条底面直径纵向剖开,量得一个纵剖面面积是6平方分米,那么,圆柱的侧面积是多少平方分米
3.14×6=18.84(平方分米)
拓展练习
纵剖面面积=dh
圆柱侧面积=πdh
5、将一个圆柱沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米
拓展练习
(1)增加的面积是什么部分?
增加的面积是2个切开的纵剖面。
(2)切开的一个纵剖面面积是怎么计算出来的?
底面直径×高
(3)圆柱的高你能算出来吗?
20÷4=5(厘米)
(4)圆柱的体积你能算出来吗?
π×5=62.8()
(1)把长、宽、高平均分成的份数:(5+4+3)×4=48
(5)纸的面积:(2.5×2+2.5×1.5+2×1.5)×2=23.5(dm2)
(6)体积:2.5×2×1.5=7.5(dm3)
6、用一根长24dm的铁丝做一个长方体框架,使它的长、宽、高的比为5:4:3。在这 个长方体框架外面糊一层纸,至少需要多少平方分米的纸?它的体积是多少立方分米?
拓展练习
拓展练习
7、
下面这些图形是从什么角度看到的?
从左面
从下面
从前面
拓展练习
8、
F
E
B的长和宽;A的宽。
(1)小正方体的个数:
63÷23=27(个)
(2)表面积增加了:
62×6-22×6=192(cm2)
9、把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体?表面积增加了多少?
拓展练习
(1)正方体体积: 103=1000(cm3)
(2)圆锥的底面积:3.14×(10÷2)2=78.5(cm2)
(3)圆锥的高:1000×3÷78.5≈38(cm)
10、把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块,这个圆锥形铁块的高约是多少?(得数保留整厘米数)
拓展练习
拓展练习
11
(1)工作1分钟前进了多少米其实是求什么?
求15 倍的前轮周长。
15×3.14×1=47.1(米)
(2)工作1分钟压过的路面面积是多少平方米其实是求什么?
求15 倍的侧面积。
15×3.14×1×1.2=56.52(平方米)
(1)表面积:
202×5+3.14×102+2×3.14×10×20÷2
=2000+314+628
=2942(cm2)
(2)体积:
203+3.14×102×20÷2
=8000+3140
=11140(cm3)
拓展练习
12.
(1)10个正方体。
(2)体积:53×10=1250(cm3)
(3)表面积:52×34=850(cm2)
13.
拓展练习
14.
拓展练习
拓展练习
15.
课后作业
完成本课时的相关习题。
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
