苏教版数学四年级下册7、《图形王国》课件(20张)
文档属性
| 名称 | 苏教版数学四年级下册7、《图形王国》课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 00:00:00 | ||
图片预览

文档简介
(共20张PPT)
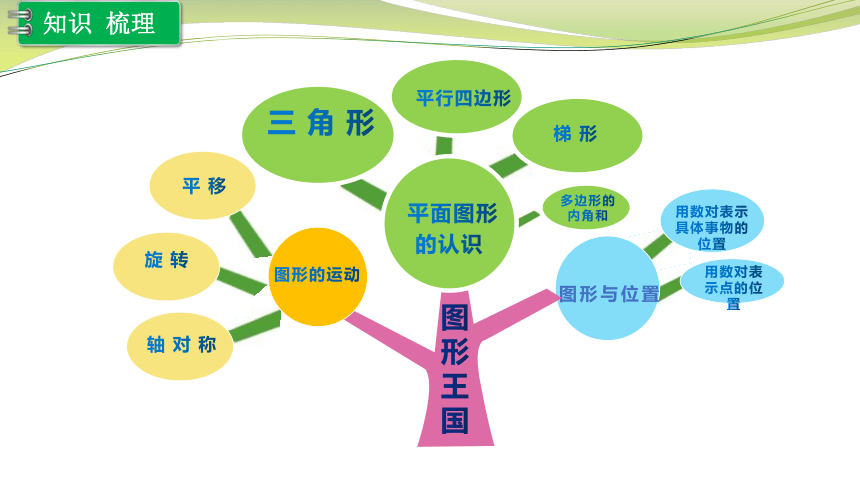
图 形 王 国
苏教版 四年级下册
图形与位置
图
形
王
国
平面图形
的认识
平 移
旋 转
轴 对 称
三 角 形
平行四边形
梯 形
图形的运动
知识 梳理
用数对表示具体事物的位置
用数对表示点的位置
多边形的内角和
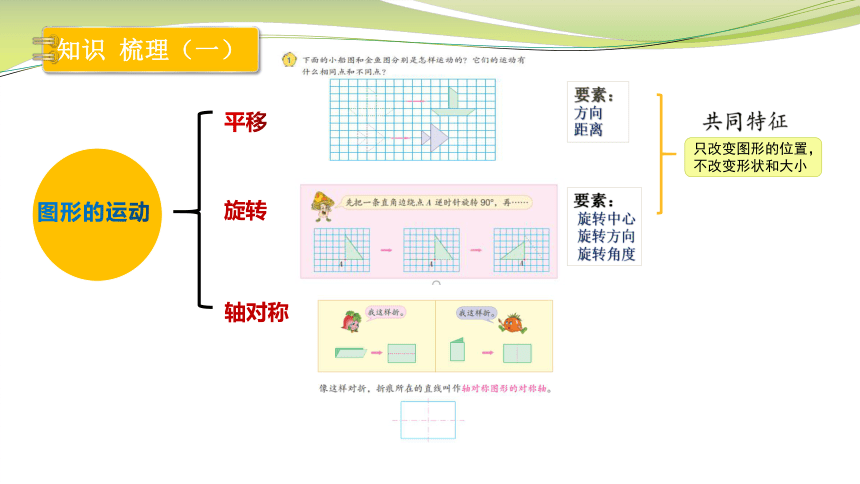
知识 梳理(一)
平移
旋转
轴对称
共同特征
要素:
方向
距离
要素:
旋转中心
旋转方向
旋转角度
图形的运动
只改变图形的位置,不改变形状和大小
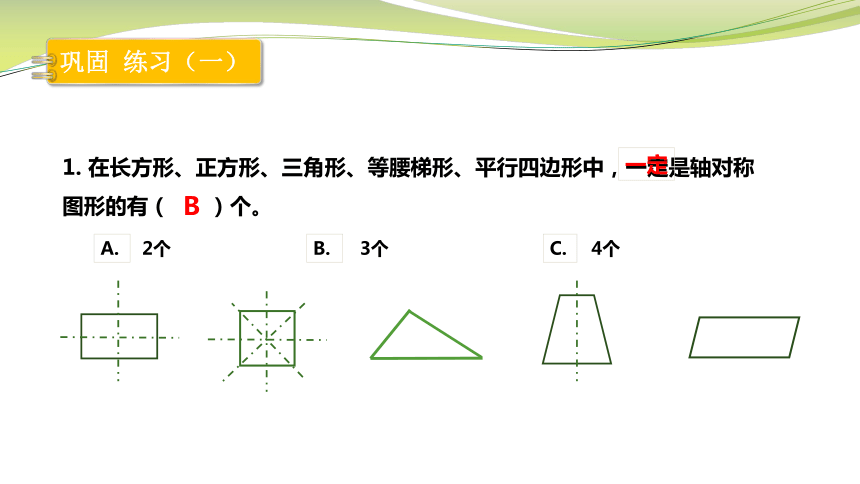
1. 在长方形、正方形、三角形、等腰梯形、平行四边形中,一定是轴对称图形的有( )个。
A.
B.
C.
2个
3个
4个
B
一定
巩固 练习(一)
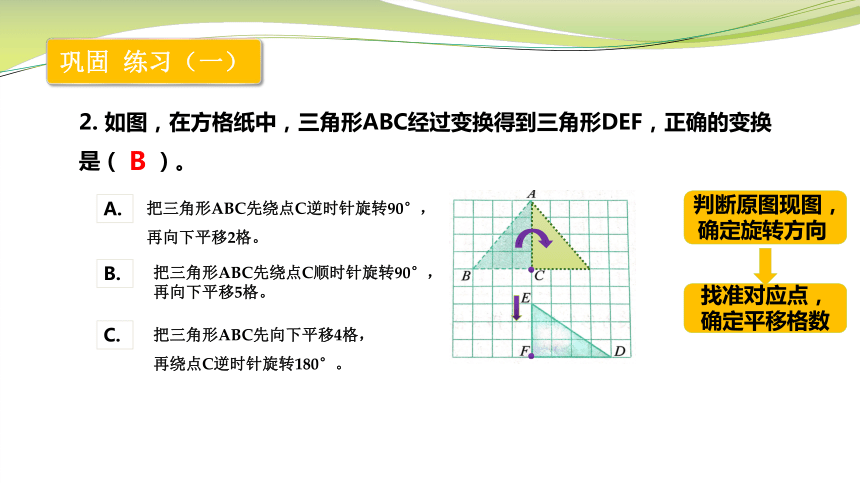
2. 如图,在方格纸中,三角形ABC经过变换得到三角形DEF,正确的变换是( )。
把三角形ABC先绕点C逆时针旋转90°,
再向下平移2格。
A.
B.
C.
把三角形ABC先绕点C顺时针旋转90°,
再向下平移5格。
把三角形ABC先向下平移4格,
再绕点C逆时针旋转180°。
B
判断原图现图,确定旋转方向
找准对应点,确定平移格数
巩固 练习(一)
用数对表示具体事物
用数对表示点的位置
用数对
确定位置
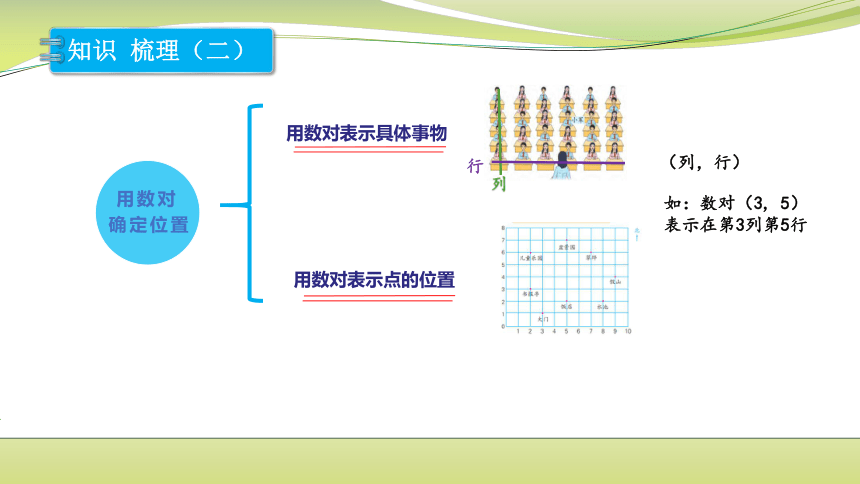
知识 梳理(二)
列
(列,行)
行
如:数对(3, 5)表示在第3列第5行
3.
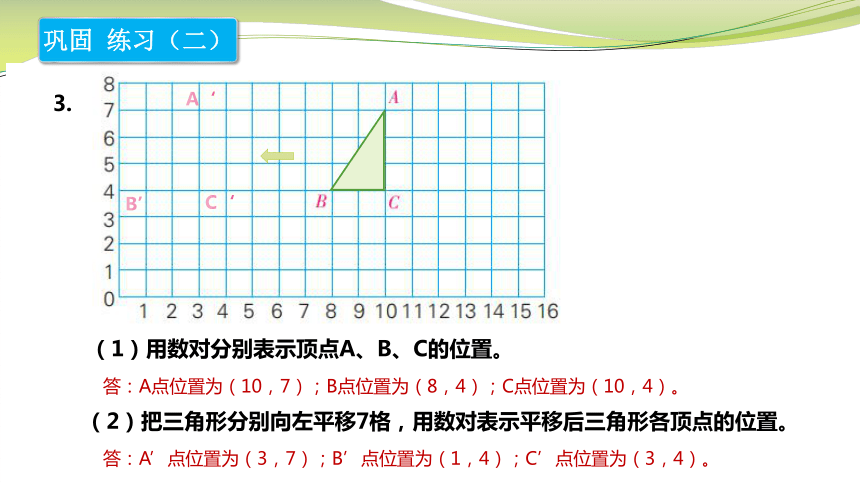
(2)把三角形分别向左平移7格,用数对表示平移后三角形各顶点的位置。
答:A’点位置为(3,7);B’点位置为(1,4);C’点位置为(3,4)。
A‘
B’
C‘
巩固 练习(二)
(1)用数对分别表示顶点A、B、C的位置。
答:A点位置为(10,7);B点位置为(8,4);C点位置为(10,4)。
3.
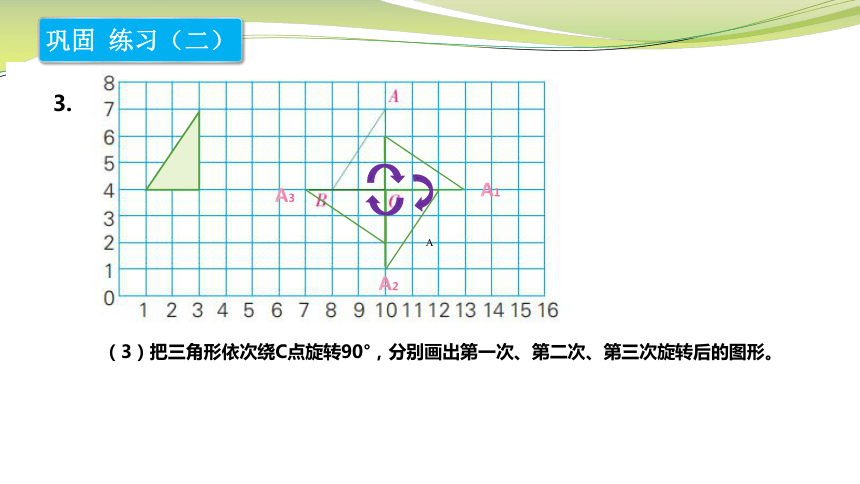
(3)把三角形依次绕C点旋转90°,分别画出第一次、第二次、第三次旋转后的图形。
A1
A2
A3
巩固 练习(二)
3.
A1
A2
A3
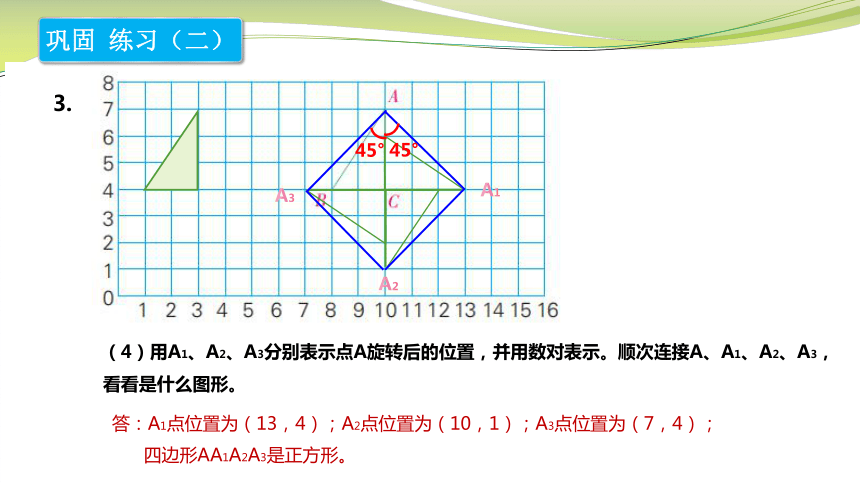
(4)用A1、A2、A3分别表示点A旋转后的位置,并用数对表示。顺次连接A、A1、A2、A3,看看是什么图形。
四边形AA1A2A3是正方形。
答:A1点位置为(13,4);A2点位置为(10,1);A3点位置为(7,4);
45°
45°
巩固 练习(二)
三角形
定义、底和高
三边关系
内角和
四边形
梯 形
认识常见的
平面图形
C
B
A
三角形任意两边长度的和大于第三边。
三角形的内角和等于180°。
三角形
等腰三角形
等边三角形
a
c
b
知识 梳理(三)
平行四边形
三条线段首尾相接围成的图形叫作三角形。
三角形的分类
等腰三角形
等边三角形
三角形
定义、底和高
三边关系
内角和
三角形分类
等腰三角形
三角形的特征
四
边
形
平行四边形
梯 形
定义、特征
底和高
定义、特征
认识常见的
平面图形
三角形的关系
两组对边分别平行的
四边形叫平行四边形。
只有一组对边平行的四边形叫梯形。
底和高
底
高
底
高
下底
高
三条线段首尾相接围成的图形叫作三角形。
等边三角形
等腰梯形、直角梯形
知识 梳理(三)
边的位置关系
腰
腰
上底
三角形
定义、底和高
三边关系
内角和
分类
按角分
按边分
三角形的特征
四边形
平行四边形
梯 形
定义、特征
底和高
定义、特征
关系
认识常见的
平面图形
三角形的关系
底和高
底
高
底
高
下底
高
特 征
关系
知识 梳理(三)
多边形的内角和
内角和=(边数-2)×180°
边数=内角和÷180°+2
上底
4. 下面的两条直线互相平行,图中的三个图形各有什么特点?
答:这些高的长度都相等;平行线之间的距离处处相等。
10厘米
8厘米
平行四边形的两条邻边分别是8厘米和10厘米,一条高是9厘米,与这条高对应的底是( )厘米。
10厘米
8
综合 练习(三)
8厘米
5. 下面每种小棒各有2根。
3 厘米
5 厘米
4 厘米
2 厘米
(1)任选3根小棒围三角形,是不是都能围成?你能围出什么三角形,是怎样围的?
3根不同的小棒:
3 厘米、4厘米、5厘米;
3 厘米、4厘米、2厘米;
4 厘米、5厘米、2厘米;
3 厘米、5厘米、2厘米;
2根相同的小棒:
3 厘米、3厘米、4厘米;
3 厘米、3厘米、5厘米;
3 厘米、3厘米、2厘米;
4 厘米、4厘米、3厘米;
4 厘米、4厘米、5厘米;
4 厘米、4厘米、2厘米;
5 厘米、5厘米、3厘米;
5 厘米、5厘米、4厘米;
5 厘米、5厘米、2厘米;
2 厘米、2厘米、3厘米;
2 厘米、2厘米、4厘米;
2 厘米、2厘米、5厘米;
合理分类
有序列举
满足三边关系
3 厘米、5厘米、2厘米;
2 厘米、2厘米、4厘米;
2 厘米、2厘米、5厘米;
各有2根
选3根
综合 练习(三)
2厘米、2厘米、4厘米;
2厘米、2厘米、5厘米;
2厘米、3厘米、5厘米不能围成三角形。
5. 下面每种小棒各有2根。
3 厘米
5 厘米
4 厘米
2 厘米
(2)要围出平行四边形,最多用几种不同的小棒?最少呢?
最多用4种小棒
最少用2种小棒
......
......
你能把围出的平行四边形围成长方形或正方形吗?这些图形之间有什么关系?
......
综合 练习(三)
平行四边形
长方形
正方形
5. 下面每种小棒各有2根。
3 厘米
5 厘米
4 厘米
2 厘米
(3)要围出梯形,最多用几种不同的小棒?最少呢?
......
......
最多用4种小棒
最少用2种小棒
综合 练习(三)
6. (1)在三角形中,已知∠1=53°,∠2=27°,求∠3.
根据三角形内角和:∠1+∠2+∠3=180°,
∠3=180°-(∠1+∠2)
=180°-(53°+27°)
=180°-80°
=100°
(2)等腰三角形一个底角是40°,它的顶角是多少度?它又是什么三角形?
如果顶角是40°呢?
在等腰三角形中,顶角=180°-底角-底角,
180°-40°-40°=100°
答:顶角为100°,这是一个是钝角三角形。
在等腰三角形中,底角=(180°-顶角)÷2,
(180°-40°)÷2=70°
答:底角为100°,这是一个是锐角三角形。
答:∠3度数为100°。
1
2
顶角
底角
底角
综合 练习(三)
3
下面的三角形ABC中,∠B=60°,若沿图中的虚线剪去∠B,
则∠1和∠2的和是多少度?
A
B
C
D
E
1
2
根据三角形的内角和为180°,
∠B=60°,
∠A+∠C=180°-60°
=120°
再根据四边形ACED的内角和为360°,
∠A+∠C=120,
∠1+∠2=360°-120°
=240°
或根据三角形的内角和为180°,
∠B=60°
∠BDE+∠BED=120,
∠1+∠2=180°+180°-120°
=240°
思考题
古人云:温故而知新,可以为师矣!
同学们再见
图 形 王 国
苏教版 四年级下册
图形与位置
图
形
王
国
平面图形
的认识
平 移
旋 转
轴 对 称
三 角 形
平行四边形
梯 形
图形的运动
知识 梳理
用数对表示具体事物的位置
用数对表示点的位置
多边形的内角和
知识 梳理(一)
平移
旋转
轴对称
共同特征
要素:
方向
距离
要素:
旋转中心
旋转方向
旋转角度
图形的运动
只改变图形的位置,不改变形状和大小
1. 在长方形、正方形、三角形、等腰梯形、平行四边形中,一定是轴对称图形的有( )个。
A.
B.
C.
2个
3个
4个
B
一定
巩固 练习(一)
2. 如图,在方格纸中,三角形ABC经过变换得到三角形DEF,正确的变换是( )。
把三角形ABC先绕点C逆时针旋转90°,
再向下平移2格。
A.
B.
C.
把三角形ABC先绕点C顺时针旋转90°,
再向下平移5格。
把三角形ABC先向下平移4格,
再绕点C逆时针旋转180°。
B
判断原图现图,确定旋转方向
找准对应点,确定平移格数
巩固 练习(一)
用数对表示具体事物
用数对表示点的位置
用数对
确定位置
知识 梳理(二)
列
(列,行)
行
如:数对(3, 5)表示在第3列第5行
3.
(2)把三角形分别向左平移7格,用数对表示平移后三角形各顶点的位置。
答:A’点位置为(3,7);B’点位置为(1,4);C’点位置为(3,4)。
A‘
B’
C‘
巩固 练习(二)
(1)用数对分别表示顶点A、B、C的位置。
答:A点位置为(10,7);B点位置为(8,4);C点位置为(10,4)。
3.
(3)把三角形依次绕C点旋转90°,分别画出第一次、第二次、第三次旋转后的图形。
A1
A2
A3
巩固 练习(二)
3.
A1
A2
A3
(4)用A1、A2、A3分别表示点A旋转后的位置,并用数对表示。顺次连接A、A1、A2、A3,看看是什么图形。
四边形AA1A2A3是正方形。
答:A1点位置为(13,4);A2点位置为(10,1);A3点位置为(7,4);
45°
45°
巩固 练习(二)
三角形
定义、底和高
三边关系
内角和
四边形
梯 形
认识常见的
平面图形
C
B
A
三角形任意两边长度的和大于第三边。
三角形的内角和等于180°。
三角形
等腰三角形
等边三角形
a
c
b
知识 梳理(三)
平行四边形
三条线段首尾相接围成的图形叫作三角形。
三角形的分类
等腰三角形
等边三角形
三角形
定义、底和高
三边关系
内角和
三角形分类
等腰三角形
三角形的特征
四
边
形
平行四边形
梯 形
定义、特征
底和高
定义、特征
认识常见的
平面图形
三角形的关系
两组对边分别平行的
四边形叫平行四边形。
只有一组对边平行的四边形叫梯形。
底和高
底
高
底
高
下底
高
三条线段首尾相接围成的图形叫作三角形。
等边三角形
等腰梯形、直角梯形
知识 梳理(三)
边的位置关系
腰
腰
上底
三角形
定义、底和高
三边关系
内角和
分类
按角分
按边分
三角形的特征
四边形
平行四边形
梯 形
定义、特征
底和高
定义、特征
关系
认识常见的
平面图形
三角形的关系
底和高
底
高
底
高
下底
高
特 征
关系
知识 梳理(三)
多边形的内角和
内角和=(边数-2)×180°
边数=内角和÷180°+2
上底
4. 下面的两条直线互相平行,图中的三个图形各有什么特点?
答:这些高的长度都相等;平行线之间的距离处处相等。
10厘米
8厘米
平行四边形的两条邻边分别是8厘米和10厘米,一条高是9厘米,与这条高对应的底是( )厘米。
10厘米
8
综合 练习(三)
8厘米
5. 下面每种小棒各有2根。
3 厘米
5 厘米
4 厘米
2 厘米
(1)任选3根小棒围三角形,是不是都能围成?你能围出什么三角形,是怎样围的?
3根不同的小棒:
3 厘米、4厘米、5厘米;
3 厘米、4厘米、2厘米;
4 厘米、5厘米、2厘米;
3 厘米、5厘米、2厘米;
2根相同的小棒:
3 厘米、3厘米、4厘米;
3 厘米、3厘米、5厘米;
3 厘米、3厘米、2厘米;
4 厘米、4厘米、3厘米;
4 厘米、4厘米、5厘米;
4 厘米、4厘米、2厘米;
5 厘米、5厘米、3厘米;
5 厘米、5厘米、4厘米;
5 厘米、5厘米、2厘米;
2 厘米、2厘米、3厘米;
2 厘米、2厘米、4厘米;
2 厘米、2厘米、5厘米;
合理分类
有序列举
满足三边关系
3 厘米、5厘米、2厘米;
2 厘米、2厘米、4厘米;
2 厘米、2厘米、5厘米;
各有2根
选3根
综合 练习(三)
2厘米、2厘米、4厘米;
2厘米、2厘米、5厘米;
2厘米、3厘米、5厘米不能围成三角形。
5. 下面每种小棒各有2根。
3 厘米
5 厘米
4 厘米
2 厘米
(2)要围出平行四边形,最多用几种不同的小棒?最少呢?
最多用4种小棒
最少用2种小棒
......
......
你能把围出的平行四边形围成长方形或正方形吗?这些图形之间有什么关系?
......
综合 练习(三)
平行四边形
长方形
正方形
5. 下面每种小棒各有2根。
3 厘米
5 厘米
4 厘米
2 厘米
(3)要围出梯形,最多用几种不同的小棒?最少呢?
......
......
最多用4种小棒
最少用2种小棒
综合 练习(三)
6. (1)在三角形中,已知∠1=53°,∠2=27°,求∠3.
根据三角形内角和:∠1+∠2+∠3=180°,
∠3=180°-(∠1+∠2)
=180°-(53°+27°)
=180°-80°
=100°
(2)等腰三角形一个底角是40°,它的顶角是多少度?它又是什么三角形?
如果顶角是40°呢?
在等腰三角形中,顶角=180°-底角-底角,
180°-40°-40°=100°
答:顶角为100°,这是一个是钝角三角形。
在等腰三角形中,底角=(180°-顶角)÷2,
(180°-40°)÷2=70°
答:底角为100°,这是一个是锐角三角形。
答:∠3度数为100°。
1
2
顶角
底角
底角
综合 练习(三)
3
下面的三角形ABC中,∠B=60°,若沿图中的虚线剪去∠B,
则∠1和∠2的和是多少度?
A
B
C
D
E
1
2
根据三角形的内角和为180°,
∠B=60°,
∠A+∠C=180°-60°
=120°
再根据四边形ACED的内角和为360°,
∠A+∠C=120,
∠1+∠2=360°-120°
=240°
或根据三角形的内角和为180°,
∠B=60°
∠BDE+∠BED=120,
∠1+∠2=180°+180°-120°
=240°
思考题
古人云:温故而知新,可以为师矣!
同学们再见
