小学数学苏教版五年级下第一单元简易方程课件(共25张PPT)
文档属性
| 名称 | 小学数学苏教版五年级下第一单元简易方程课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 10:50:09 | ||
图片预览






文档简介
(共25张PPT)
简易方程单元整理与复习
我认识了方程,知道了等式的形式。
我学会了用等式的性质解方程。
我能列方程解决实际问题。
……
1. 举例说说方程、 方程的解和解方程的含义。
像x+50=150、2x=200这样含有未知数的等式是方程。
使方程左右两边相等的未知数的值叫作方程的解。
求方程的解的过程叫作解方程。
回顾整理
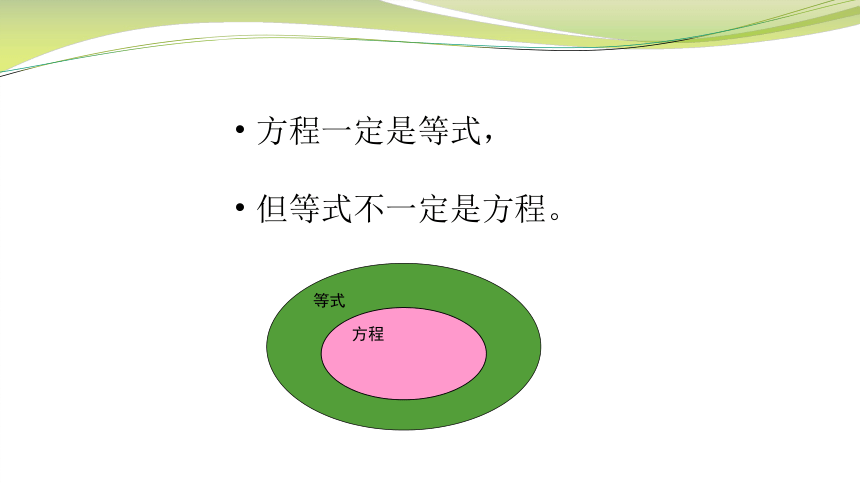
方程一定是等式,
但等式不一定是方程。
等式
方程
典题精讲
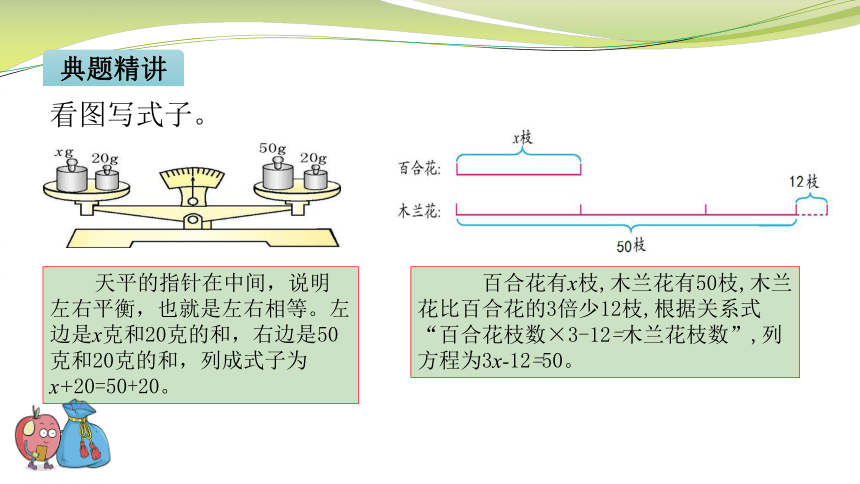
看图写式子。
天平的指针在中间,说明左右平衡,也就是左右相等。左边是x克和20克的和,右边是50克和20克的和,列成式子为x+20=50+20。
百合花有x枝,木兰花有50枝,木兰花比百合花的3倍少12枝,根据关系式“百合花枝数×3-12=木兰花枝数”,列方程为3x-12=50。
它们是方程吗?你是怎样想的?
(1)x-31=12 (5)35+65=100
(2)y+24 (6)x-14>72
(3)28<16+14 (7)9b-30=60
(4)6(y+2)=42 (8)x+y=70
学以致用
判断题:
(1)含有未知数的等式是方程( )
(2)含有未知数的式子是方程( )
(3)方程是等式,等式也是方程( )
(4)3χ=0是方程( )
(5)4χ+20含有未知数,所以它是方程( )
√
X
X
√
X
学以致用
解方程:
180+6x=330
解: 6x =330-180
6x=150
x=25
典题精讲
x-0.8x=10
解: 0.2x=10
x=50
1. 解方程时要写解,等于号要对齐
解方程的注意点
2. 要根据等式的基本性质来解方程。
(1)等式的左右两边同时加上或减去一个相同的数,所得的结果仍然是等式。
(2)等式的左右两边同时乘或除以一个相同的数(0除外),所得的结果仍然是等式。
3. 解完方程要检验。
学校印制画册一共用去2240元,画册的印刷费是3.6元/本,其余费用是800元。学校印制了多少本画册?
解:
设学校印制了 x 本画册。
3.6 x + 800 = 2240
3.6 x = 1440
x = 400
答:学校印制了400本画册。
典题精讲
画册印刷费+其余费用=一共用去多少元
检验结果是否正确,并思考还能怎样列方程解答。
用一根长72厘米的铁丝围成一个长方形,要使长是宽的2倍,围成的长方形的长和宽各是多少厘米 (接头处忽略不计)
解:设围成的长方形的宽是x厘米,则长是2x厘米。
(x+2x)×2=72
x=12
2x=2×12=24
答:围成的长方形的宽是12厘米,长是24厘米。
典题精讲
(长+宽)×2=长方形周长
典题精讲
妈妈把家里的小鸡和兔子放在一个笼子里, 笼子里一共有42只脚,有11个头。小鸡和兔子各有几只
解题思路:
用方程解决问题中,如果有两个未知量,可设其中标准量为x,另一个未知量用含有x的式子表示,然后根据题中的数量关系列出方程,此题中可以设小鸡为x只,则兔子有(11-x)只;也可以设兔子为x只,则小鸡有(11-x)只。
典题精讲
妈妈把家里的小鸡和兔子放在一个笼子里, 笼子里一共有42只脚,有11个头。小鸡和兔子各有几只
解:设兔子有x只,鸡有(11-x)只。
4x+2(11-x)=42
4x+2×11-2x=42
2x+22=42
2x=42-22
2x=20
x=10
11-x=1
答:小鸡有1只,兔子有10只。
1. 读题,弄清题意,找出已知条件和所求问题。
2. 列出等量关系式,设所求问题为x。
3. 列方程再解方程。注意x 不带单位。
4. 检验,写出答案。
列方程解决实际问题的步骤:
巩固练习
1. 不计算,把下列每组方程中代表数值最大的字母圈出来。
x+2=20 y+3=20 z+4=20
x÷2=36 y÷3=36 z÷4=36
题中给出了两组方程,每组方程的形式相同,未知数分别为x、y、z。观察第一组,和相等,则已知加数越小,未知加数越大。第二组, 商相等,则除数越大,被除数越大。
解题思路:
巩固练习
x+2=20 y+3=20 z+4=20
x÷2=36 y÷3=36 z÷4=36
正确解答:
2. 同学们参观“远离毒品”展览。四、五年级一共去了264人,五年级去的 人数是四年级1.2倍。两个年级各去了多少人?
巩固练习
解:设四年级去了x人,五年级去了1.2x人。
x+1.2x=264
2.2x=264
x=120
1.2x=1.2×120=144
答:四年级去了120人,五年级去了144人。
3. 猎豹追逐猎物时的速度大约是优秀短跑运动员百米赛跑速度的3倍,每秒大约比运动员多跑20米。优秀短跑运动员每秒大约跑多少米?猎豹呢?
数量关系式是什么?
猎豹每秒的速度-优秀短跑运动员每秒的速度= 20米
3. 猎豹追逐猎物时的速度大约是优秀短跑运动员百米赛跑速度的3倍,每秒大约比运动员多跑20米。优秀短跑运动员每秒大约跑多少米?猎豹呢?
解:
设优秀短跑运动员每秒大约跑 x 米,则猎豹每秒大约跑 3x 米。
3 x - x = 20
2 x = 20
x = 10
答:优秀短跑运动员每秒大约跑10米,猎豹每秒大约跑30米。
3 x = 3 × 10 = 30
我买8张光盘。
两人一共要付126元。
我买10张光盘。
每张光盘多少元?
左边孩子买光盘的元数 + 右边孩子买光盘的元数 = 126元
4.
光盘的单价 × 两个孩子买的总数量 = 126元
我买8张光盘。
两人一共要付126元。
我买10张光盘。
解:设每张光盘 x 元。
8 x +10 x = 216
18 x = 216
答:每张光盘12元。
x = 12
(8+10) x = 216
18 x = 216
x = 12
每张光盘多少元?
4.
5.
甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是280米/分,乙的速度是240米/分。经过多少分钟甲第一次追上乙?
解:
设经过 x 分钟甲第一次追上乙。
280 x - 240 x = 400
40 x = 400
x = 10
答:经过10分钟甲第一次追上乙。
(280 - 240)x = 400
40 x = 400
x = 10
甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是280米/分,乙的速度是240米/分。经过多少分钟甲第一次追上乙?
5.
1.解方程时能化简的要化简,能先计算的要先计算,然后应用等式的性质求方程的解。
2.找准数量间的等量关系是列方程解决问题的关键。
课堂小结
简易方程单元整理与复习
我认识了方程,知道了等式的形式。
我学会了用等式的性质解方程。
我能列方程解决实际问题。
……
1. 举例说说方程、 方程的解和解方程的含义。
像x+50=150、2x=200这样含有未知数的等式是方程。
使方程左右两边相等的未知数的值叫作方程的解。
求方程的解的过程叫作解方程。
回顾整理
方程一定是等式,
但等式不一定是方程。
等式
方程
典题精讲
看图写式子。
天平的指针在中间,说明左右平衡,也就是左右相等。左边是x克和20克的和,右边是50克和20克的和,列成式子为x+20=50+20。
百合花有x枝,木兰花有50枝,木兰花比百合花的3倍少12枝,根据关系式“百合花枝数×3-12=木兰花枝数”,列方程为3x-12=50。
它们是方程吗?你是怎样想的?
(1)x-31=12 (5)35+65=100
(2)y+24 (6)x-14>72
(3)28<16+14 (7)9b-30=60
(4)6(y+2)=42 (8)x+y=70
学以致用
判断题:
(1)含有未知数的等式是方程( )
(2)含有未知数的式子是方程( )
(3)方程是等式,等式也是方程( )
(4)3χ=0是方程( )
(5)4χ+20含有未知数,所以它是方程( )
√
X
X
√
X
学以致用
解方程:
180+6x=330
解: 6x =330-180
6x=150
x=25
典题精讲
x-0.8x=10
解: 0.2x=10
x=50
1. 解方程时要写解,等于号要对齐
解方程的注意点
2. 要根据等式的基本性质来解方程。
(1)等式的左右两边同时加上或减去一个相同的数,所得的结果仍然是等式。
(2)等式的左右两边同时乘或除以一个相同的数(0除外),所得的结果仍然是等式。
3. 解完方程要检验。
学校印制画册一共用去2240元,画册的印刷费是3.6元/本,其余费用是800元。学校印制了多少本画册?
解:
设学校印制了 x 本画册。
3.6 x + 800 = 2240
3.6 x = 1440
x = 400
答:学校印制了400本画册。
典题精讲
画册印刷费+其余费用=一共用去多少元
检验结果是否正确,并思考还能怎样列方程解答。
用一根长72厘米的铁丝围成一个长方形,要使长是宽的2倍,围成的长方形的长和宽各是多少厘米 (接头处忽略不计)
解:设围成的长方形的宽是x厘米,则长是2x厘米。
(x+2x)×2=72
x=12
2x=2×12=24
答:围成的长方形的宽是12厘米,长是24厘米。
典题精讲
(长+宽)×2=长方形周长
典题精讲
妈妈把家里的小鸡和兔子放在一个笼子里, 笼子里一共有42只脚,有11个头。小鸡和兔子各有几只
解题思路:
用方程解决问题中,如果有两个未知量,可设其中标准量为x,另一个未知量用含有x的式子表示,然后根据题中的数量关系列出方程,此题中可以设小鸡为x只,则兔子有(11-x)只;也可以设兔子为x只,则小鸡有(11-x)只。
典题精讲
妈妈把家里的小鸡和兔子放在一个笼子里, 笼子里一共有42只脚,有11个头。小鸡和兔子各有几只
解:设兔子有x只,鸡有(11-x)只。
4x+2(11-x)=42
4x+2×11-2x=42
2x+22=42
2x=42-22
2x=20
x=10
11-x=1
答:小鸡有1只,兔子有10只。
1. 读题,弄清题意,找出已知条件和所求问题。
2. 列出等量关系式,设所求问题为x。
3. 列方程再解方程。注意x 不带单位。
4. 检验,写出答案。
列方程解决实际问题的步骤:
巩固练习
1. 不计算,把下列每组方程中代表数值最大的字母圈出来。
x+2=20 y+3=20 z+4=20
x÷2=36 y÷3=36 z÷4=36
题中给出了两组方程,每组方程的形式相同,未知数分别为x、y、z。观察第一组,和相等,则已知加数越小,未知加数越大。第二组, 商相等,则除数越大,被除数越大。
解题思路:
巩固练习
x+2=20 y+3=20 z+4=20
x÷2=36 y÷3=36 z÷4=36
正确解答:
2. 同学们参观“远离毒品”展览。四、五年级一共去了264人,五年级去的 人数是四年级1.2倍。两个年级各去了多少人?
巩固练习
解:设四年级去了x人,五年级去了1.2x人。
x+1.2x=264
2.2x=264
x=120
1.2x=1.2×120=144
答:四年级去了120人,五年级去了144人。
3. 猎豹追逐猎物时的速度大约是优秀短跑运动员百米赛跑速度的3倍,每秒大约比运动员多跑20米。优秀短跑运动员每秒大约跑多少米?猎豹呢?
数量关系式是什么?
猎豹每秒的速度-优秀短跑运动员每秒的速度= 20米
3. 猎豹追逐猎物时的速度大约是优秀短跑运动员百米赛跑速度的3倍,每秒大约比运动员多跑20米。优秀短跑运动员每秒大约跑多少米?猎豹呢?
解:
设优秀短跑运动员每秒大约跑 x 米,则猎豹每秒大约跑 3x 米。
3 x - x = 20
2 x = 20
x = 10
答:优秀短跑运动员每秒大约跑10米,猎豹每秒大约跑30米。
3 x = 3 × 10 = 30
我买8张光盘。
两人一共要付126元。
我买10张光盘。
每张光盘多少元?
左边孩子买光盘的元数 + 右边孩子买光盘的元数 = 126元
4.
光盘的单价 × 两个孩子买的总数量 = 126元
我买8张光盘。
两人一共要付126元。
我买10张光盘。
解:设每张光盘 x 元。
8 x +10 x = 216
18 x = 216
答:每张光盘12元。
x = 12
(8+10) x = 216
18 x = 216
x = 12
每张光盘多少元?
4.
5.
甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是280米/分,乙的速度是240米/分。经过多少分钟甲第一次追上乙?
解:
设经过 x 分钟甲第一次追上乙。
280 x - 240 x = 400
40 x = 400
x = 10
答:经过10分钟甲第一次追上乙。
(280 - 240)x = 400
40 x = 400
x = 10
甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是280米/分,乙的速度是240米/分。经过多少分钟甲第一次追上乙?
5.
1.解方程时能化简的要化简,能先计算的要先计算,然后应用等式的性质求方程的解。
2.找准数量间的等量关系是列方程解决问题的关键。
课堂小结
