苏教版数学六年级下册 7.2 生活中的立体图形 课件(17张ppt)
文档属性
| 名称 | 苏教版数学六年级下册 7.2 生活中的立体图形 课件(17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 13:32:41 | ||
图片预览






文档简介
(共17张PPT)
生活中的立体图形
义务教育小学数学六年级下册
例1:求下面图形的体积。(单位:厘米)
V总=V1+ V2+ V3
V2
V1
V3
V4
+V4
V1:3×3×9=81(立方厘米)
V2:3×3×6=54(立方厘米)
V3:3×3×12=108(立方厘米)
V4:3×3×3=27(立方厘米)
V总:81+54+108+27=270(立方厘米)
V总:3×3×(3+6+9+12)=9×30=270(立方厘米)
虽然看不见,
但要想得到。
想象
同步练习1:求下面图形的体积和表面积。(单位:厘米)
V总=V1+ V2
(6÷2)2π×3 +(10÷2)2π×4
= 27π +100π
= 127π (立方厘米)
S总=S大表+ S小表
-2 S小底
(10÷2)2π×2+10π×4 +6π×3
=S大表+S小侧
=50π+40π+18π
=108π(平方厘米)
108π=339.12(平方厘米)
例2:求下面蛋筒的体积。(单位:厘米)
15
2
例2:求下面蛋筒的体积。(单位:厘米)
V总=V1+ V2
h1
15
2
h2
2×2×π×h1÷3
2×2×π×h2÷3
+
=4×π×h1÷3 +4×π×h2÷3
=4×π×(h1+h2)÷3
=4×π×15÷3
=20π(立方厘米)
2
22×π×15÷3
=20π(立方厘米)
转化
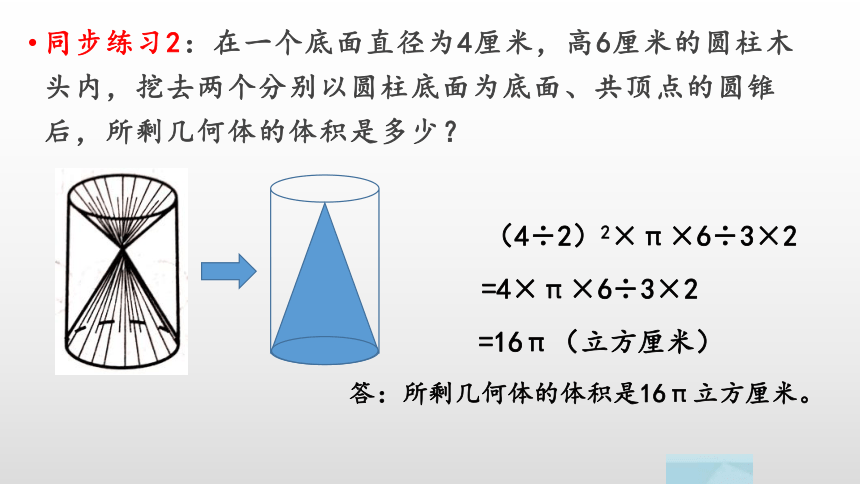
同步练习2:在一个底面直径为4厘米,高6厘米的圆柱木头内,挖去两个分别以圆柱底面为底面、共顶点的圆锥后,所剩几何体的体积是多少?
(4÷2)2×π×6÷3×2
=4×π×6÷3×2
=16π(立方厘米)
答:所剩几何体的体积是16π立方厘米。
例3:一个饮料瓶,它的瓶身呈圆柱形(不计瓶颈),如下图所示,已知它的容积是1200毫升,当瓶子正放时瓶内水面高为18厘米,倒放时瓶内空余部分高为6厘米,瓶内装有多少毫升的饮料?
6
18+6=24(厘米)
1200÷24=50(平方厘米)
50×18=900(立方厘米)=900(毫升)
方法1:
方法2:
1200×
=900(毫升 )
同步练习3:如图,一个瓶里面深24厘米,底面直径是16厘米,瓶里水深15厘米。把瓶塞紧后,使其瓶口向下倒立,这时水深19厘米。瓶的容积是多少毫升?
V总 = V水 + V空
V水
V空
(16÷2)2×π×15+(16÷2)2×π×(24-19)
=(16÷2)2×π×[15+(24-19)]
=64π×20
=1280π(立方厘米)
=1280π(毫升)
答:瓶的容积是1280π毫升。
转化
例4:利用图中的阴影部分刚好能做成一个圆柱形的油桶(接头处忽略不计)。求这个油桶的容积。
直径 = 长方形的宽
长方形的宽就是圆柱的高
阴影长方形的长就是圆柱的底面周长
d
d
πd
30.84÷(π+1+1)=30.84÷5.14
=6(dm)
(6÷2)2π×6
=9π×6
=54π(dm3)
=54π(升)
答:这个油桶的容积是 54π 升。
同步练习4:右图是一块长方形铁皮,利用图中的阴影部分,刚好能做成一个圆柱形油桶(接头处忽略不计)。求这个油桶的容积。
2条直径 = 长方形的宽
长方形的宽就是圆柱的高
阴影长方形的长就是圆柱的底面周长
d
πd
8.28÷(π+1)=8.28÷4.14
=2(dm)
(2÷2)2π×(2×2)
=1×π×4
=4π(dm3)
=12.56(升)
答:这个油桶的容积是 12.56升。
1.一种有芯卫生卷纸的高约10厘米,底面的外直径约14厘米,内直径约4厘米。一卷这种卫生卷纸的体积约是多少立方厘米?
巩固练习:
(14÷2)2×π×10-(4÷2)2×π×10
= [(14÷2)2-(4÷2)2]×π×10
= [49-4]×π×10
= 45×π×10
= 450π(立方厘米)
答:一卷这种卫生纸的体积约是 450π立方厘米。
巩固练习:
2.一个双层鲜奶蛋糕,底层的蛋糕直径长20厘米,上层的蛋糕直径长10厘米,每层蛋糕高6厘米。给这个双层蛋糕的外侧先刷上一层奶油,刷奶油的面积是多少平方厘米?如果给这个蛋糕做一个长方体包装盒(内侧距离蛋糕2厘米),包装盒用纸板多少平方厘米?
刷奶油的面积:
底层圆柱的侧面积+底层圆柱的底面积+上层圆柱的侧面积
20π×6+(20÷2)2π+10π×6
=120π+100π+60π
=280π(平方厘米)
巩固练习:
2.一个双层鲜奶蛋糕,底层的蛋糕外直径长20厘米,上层的蛋糕外直径长10厘米,每层蛋糕高6厘米。给这个双层蛋糕的外侧先刷上一层奶油,刷奶油的面积是多少平方厘米?如果给这个蛋糕做一个长方体包装盒(内侧距离蛋糕2厘米),包装盒用纸板多少平方厘米?
想一想:这个长方体包装盒是一个长、宽、高分别是多少厘米的长方体?
长:20+2+2=24厘米
←宽
高:6+6+2=14厘米
24×24×2+24×14×4
=1152+1344
=2496(平方厘米)
答:包装盒用纸板2496平方厘米。
3.李师傅擅长做兰州拉面,且拉出来的面条很细。每次他这样做:将一个面团揉成一个圆柱形面棍,长1.5米,然后对齐;再拉长到1.5米……照这样反复下去,最后拉出的面条粗细(直径)仅有原来面棍的 ,最后拉出的细面条总共长多少米?
巩固练习:
d细:d粗=1:20
S细底:S粗底=12:202
V粗:V细=?
= 1: 400
1.5×400=600(米)
答:最后拉出的细面条总共长600米。
回顾与总结
应用空间想象可以帮助我们解决立体图形问题。
应用转化的数学思想可以解决生活中的立体图形问题。
联系实际综合应用知识可以有效解决数学问题。
谢谢!
生活中的立体图形
义务教育小学数学六年级下册
例1:求下面图形的体积。(单位:厘米)
V总=V1+ V2+ V3
V2
V1
V3
V4
+V4
V1:3×3×9=81(立方厘米)
V2:3×3×6=54(立方厘米)
V3:3×3×12=108(立方厘米)
V4:3×3×3=27(立方厘米)
V总:81+54+108+27=270(立方厘米)
V总:3×3×(3+6+9+12)=9×30=270(立方厘米)
虽然看不见,
但要想得到。
想象
同步练习1:求下面图形的体积和表面积。(单位:厘米)
V总=V1+ V2
(6÷2)2π×3 +(10÷2)2π×4
= 27π +100π
= 127π (立方厘米)
S总=S大表+ S小表
-2 S小底
(10÷2)2π×2+10π×4 +6π×3
=S大表+S小侧
=50π+40π+18π
=108π(平方厘米)
108π=339.12(平方厘米)
例2:求下面蛋筒的体积。(单位:厘米)
15
2
例2:求下面蛋筒的体积。(单位:厘米)
V总=V1+ V2
h1
15
2
h2
2×2×π×h1÷3
2×2×π×h2÷3
+
=4×π×h1÷3 +4×π×h2÷3
=4×π×(h1+h2)÷3
=4×π×15÷3
=20π(立方厘米)
2
22×π×15÷3
=20π(立方厘米)
转化
同步练习2:在一个底面直径为4厘米,高6厘米的圆柱木头内,挖去两个分别以圆柱底面为底面、共顶点的圆锥后,所剩几何体的体积是多少?
(4÷2)2×π×6÷3×2
=4×π×6÷3×2
=16π(立方厘米)
答:所剩几何体的体积是16π立方厘米。
例3:一个饮料瓶,它的瓶身呈圆柱形(不计瓶颈),如下图所示,已知它的容积是1200毫升,当瓶子正放时瓶内水面高为18厘米,倒放时瓶内空余部分高为6厘米,瓶内装有多少毫升的饮料?
6
18+6=24(厘米)
1200÷24=50(平方厘米)
50×18=900(立方厘米)=900(毫升)
方法1:
方法2:
1200×
=900(毫升 )
同步练习3:如图,一个瓶里面深24厘米,底面直径是16厘米,瓶里水深15厘米。把瓶塞紧后,使其瓶口向下倒立,这时水深19厘米。瓶的容积是多少毫升?
V总 = V水 + V空
V水
V空
(16÷2)2×π×15+(16÷2)2×π×(24-19)
=(16÷2)2×π×[15+(24-19)]
=64π×20
=1280π(立方厘米)
=1280π(毫升)
答:瓶的容积是1280π毫升。
转化
例4:利用图中的阴影部分刚好能做成一个圆柱形的油桶(接头处忽略不计)。求这个油桶的容积。
直径 = 长方形的宽
长方形的宽就是圆柱的高
阴影长方形的长就是圆柱的底面周长
d
d
πd
30.84÷(π+1+1)=30.84÷5.14
=6(dm)
(6÷2)2π×6
=9π×6
=54π(dm3)
=54π(升)
答:这个油桶的容积是 54π 升。
同步练习4:右图是一块长方形铁皮,利用图中的阴影部分,刚好能做成一个圆柱形油桶(接头处忽略不计)。求这个油桶的容积。
2条直径 = 长方形的宽
长方形的宽就是圆柱的高
阴影长方形的长就是圆柱的底面周长
d
πd
8.28÷(π+1)=8.28÷4.14
=2(dm)
(2÷2)2π×(2×2)
=1×π×4
=4π(dm3)
=12.56(升)
答:这个油桶的容积是 12.56升。
1.一种有芯卫生卷纸的高约10厘米,底面的外直径约14厘米,内直径约4厘米。一卷这种卫生卷纸的体积约是多少立方厘米?
巩固练习:
(14÷2)2×π×10-(4÷2)2×π×10
= [(14÷2)2-(4÷2)2]×π×10
= [49-4]×π×10
= 45×π×10
= 450π(立方厘米)
答:一卷这种卫生纸的体积约是 450π立方厘米。
巩固练习:
2.一个双层鲜奶蛋糕,底层的蛋糕直径长20厘米,上层的蛋糕直径长10厘米,每层蛋糕高6厘米。给这个双层蛋糕的外侧先刷上一层奶油,刷奶油的面积是多少平方厘米?如果给这个蛋糕做一个长方体包装盒(内侧距离蛋糕2厘米),包装盒用纸板多少平方厘米?
刷奶油的面积:
底层圆柱的侧面积+底层圆柱的底面积+上层圆柱的侧面积
20π×6+(20÷2)2π+10π×6
=120π+100π+60π
=280π(平方厘米)
巩固练习:
2.一个双层鲜奶蛋糕,底层的蛋糕外直径长20厘米,上层的蛋糕外直径长10厘米,每层蛋糕高6厘米。给这个双层蛋糕的外侧先刷上一层奶油,刷奶油的面积是多少平方厘米?如果给这个蛋糕做一个长方体包装盒(内侧距离蛋糕2厘米),包装盒用纸板多少平方厘米?
想一想:这个长方体包装盒是一个长、宽、高分别是多少厘米的长方体?
长:20+2+2=24厘米
←宽
高:6+6+2=14厘米
24×24×2+24×14×4
=1152+1344
=2496(平方厘米)
答:包装盒用纸板2496平方厘米。
3.李师傅擅长做兰州拉面,且拉出来的面条很细。每次他这样做:将一个面团揉成一个圆柱形面棍,长1.5米,然后对齐;再拉长到1.5米……照这样反复下去,最后拉出的面条粗细(直径)仅有原来面棍的 ,最后拉出的细面条总共长多少米?
巩固练习:
d细:d粗=1:20
S细底:S粗底=12:202
V粗:V细=?
= 1: 400
1.5×400=600(米)
答:最后拉出的细面条总共长600米。
回顾与总结
应用空间想象可以帮助我们解决立体图形问题。
应用转化的数学思想可以解决生活中的立体图形问题。
联系实际综合应用知识可以有效解决数学问题。
谢谢!
