【新课标】2.5.2圆的切线(1) 课件(共29张PPT)
文档属性
| 名称 | 【新课标】2.5.2圆的切线(1) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
2.5.2圆的切线(1)
湘教版 九年级下
教学内容分析
在上节学习直线与圆的位置关系中,学习了切线的定义,这节课将学习圆的切线的判定,切线的判定定理,并学习用三角尺画圆的切线。
教学目标
1. 探究、理解切线的判定判定定理;(重点)
2. 学会用三角尺画圆的切线;
3. 掌握圆的切线的两种判定方法:切线定义和切线的判定定理,解决几何问题.(难点)
核心素养分析
本节课是需要学生理解切线的判定定理,切线经过的点,还有切线与半径的位置关系,并让学生自己动手,学会用三角尺画圆的切线。因此,本节学习判定定理主要培养了学生推理能力的素养;动手画图,锤炼了学生的动手操作能力。
新知导入
设⊙O 的半径为r,圆心O到直线l的距离为d,则有:
(1) 直线 l 和⊙O相交 d<r;
(2) 直线 l 和⊙O相切 d=r;
(3) 直线 l 和⊙O相离 d>r.
如何判定直线和圆的位置关系呢?
新知讲解
观察图2-38, 工人用砂轮磨一把刀, 在接触的一瞬间, 擦出的火花是沿着砂轮的什么方向飞出去的?
观察
图2-38
新知讲解
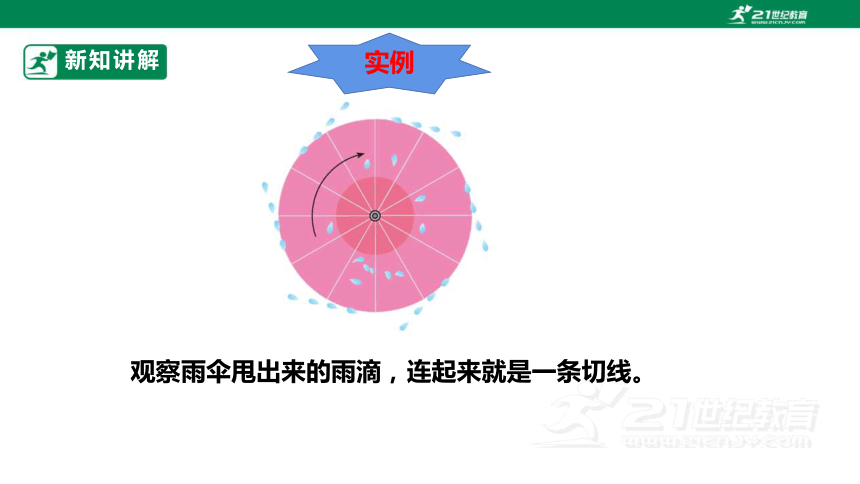
观察雨伞甩出来的雨滴,连起来就是一条切线。
实例
新知讲解
生活中,我们常常看到切线的实例,如何判断一条直线是不是⊙O 的切线呢?
新知讲解
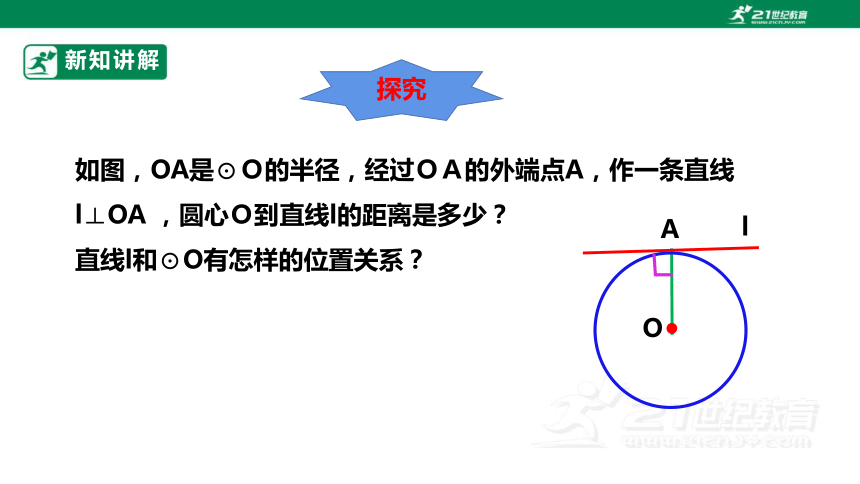
如图,OA是⊙O的半径,经过OA的外端点A,作一条直线l⊥OA ,圆心O到直线l的距离是多少?
直线l和⊙O有怎样的位置关系?
探究
A
l
O
新知讲解
由圆的切线定义可知直线l与圆O相切
A
l
O
圆心O到直线l的距离等于半径 OA
新知讲解
经过半径外端并且垂直于这条半径的直线是圆的切线.
∵OA为⊙O半径
l ⊥ OA于A
∴l 为⊙O的切线
A
l
O
语言表示:
新知讲解
用三角尺过圆上一点画圆的切线。
如图,已知⊙O上一点P,过点P画⊙O的切线.
做一做
.P
.O
新知讲解
画法:
(1)连接OP,将三角尺的直角顶点放在点P处,并使 一直角边与半径OP重合;
(2)过点P沿着三角尺的另一条直角边画直线l,则l就 是所要画的切线. 如图2-40.
.O
.P
图2-40
l
新知讲解
因为画出来的直线l符合切线的定义,l经过⊙O的半径OP的外端点P,并且l⊥OP,所以直线l是⊙O的切线.
为什么画出来的直线l是⊙O的切线呢?
新知讲解
例2 如图,已知AD是⊙O的直径,直线BC经过点D,并且AB=AC,∠BAD=∠CAD.
求证:直线BC是⊙O的切线.
点拨:由于AB=AC,利用等腰三角形的性质证明AD⊥BC。即可证明BC是⊙O的切线。
新知讲解
证明:∵ AB=AC,∠BAD=∠CAD ,
∴ AD⊥BC.
又∵ OD是⊙O的半径,且BC经过点D,
∴ 直线BC是⊙O的切线.
新知讲解
切线的判定方法:
圆心到直线的距离d等于半径r
d
r
定义:直线与圆只有一个公共点A
定理判定:证明OA⊥l
A
O
l
A
新知讲解
如图,切线的判定常作的辅助线有哪些?
(1)连半径OA,证明l与半径OA垂直;
(2)作垂直OA⊥l,证明OA=r
A
1.下列四个选项中的表述,正确的是( )
A. 经过半径上一点且垂直于这条半径的直线是圆的切线
B. 经过半径的端点且垂直于这条半径的直线是圆的切线
C. 经过半径的外端且垂直于这条半径的直线是圆的切线
D. 经过一条弦的外端且垂直于这条弦的直线是圆的切线
课堂练习
C
课堂练习
解:由切线的判定定理可知:
经过半径外端点且与这条半径垂直的直线是圆的切线,
故A,B,D,选项不正确,选项C正确,
故选C.
课堂练习
2. 如图,以点P为圆心作圆,所得的圆与直线l相切的是 ( )
A. 以PA为半径的圆 B. 以PB为半径的圆
C. 以PC为半径的圆 D. 以PD为半径的圆
C
课堂练习
解:∵PC⊥l于C,
∴以点P为圆心,PC为半径的圆与直线l相切.
故选C.
课堂练习
3. 如图,AB=BC,以BC为直径作⊙O,AC交⊙O于点E,过点E作EG⊥AB于点F,交CB的延长线于点G.
求证:EG是⊙O的切线;
课堂练习
解:连接OE.∵AB=BC,∴∠A=∠C;
∵OE=OC,∴∠OEC=∠C,
∴∠A=∠OEC,∴OE//AB,
∵BA⊥GE,
∴OE⊥EG,且OE为半径;
∴EG是⊙O的切线;
课堂总结
圆的切线
1 切线的判定定理
2. 用三角尺画圆的切线
经过半径外端并且垂直于这条半径的直线是圆的切线
板书设计
2.5.2圆的切线
1.切线的判定定理;
2.用三角尺画圆的切线;
作业布置
必做题:课本67页的练习第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.5.2圆的切线(1)
湘教版 九年级下
教学内容分析
在上节学习直线与圆的位置关系中,学习了切线的定义,这节课将学习圆的切线的判定,切线的判定定理,并学习用三角尺画圆的切线。
教学目标
1. 探究、理解切线的判定判定定理;(重点)
2. 学会用三角尺画圆的切线;
3. 掌握圆的切线的两种判定方法:切线定义和切线的判定定理,解决几何问题.(难点)
核心素养分析
本节课是需要学生理解切线的判定定理,切线经过的点,还有切线与半径的位置关系,并让学生自己动手,学会用三角尺画圆的切线。因此,本节学习判定定理主要培养了学生推理能力的素养;动手画图,锤炼了学生的动手操作能力。
新知导入
设⊙O 的半径为r,圆心O到直线l的距离为d,则有:
(1) 直线 l 和⊙O相交 d<r;
(2) 直线 l 和⊙O相切 d=r;
(3) 直线 l 和⊙O相离 d>r.
如何判定直线和圆的位置关系呢?
新知讲解
观察图2-38, 工人用砂轮磨一把刀, 在接触的一瞬间, 擦出的火花是沿着砂轮的什么方向飞出去的?
观察
图2-38
新知讲解
观察雨伞甩出来的雨滴,连起来就是一条切线。
实例
新知讲解
生活中,我们常常看到切线的实例,如何判断一条直线是不是⊙O 的切线呢?
新知讲解
如图,OA是⊙O的半径,经过OA的外端点A,作一条直线l⊥OA ,圆心O到直线l的距离是多少?
直线l和⊙O有怎样的位置关系?
探究
A
l
O
新知讲解
由圆的切线定义可知直线l与圆O相切
A
l
O
圆心O到直线l的距离等于半径 OA
新知讲解
经过半径外端并且垂直于这条半径的直线是圆的切线.
∵OA为⊙O半径
l ⊥ OA于A
∴l 为⊙O的切线
A
l
O
语言表示:
新知讲解
用三角尺过圆上一点画圆的切线。
如图,已知⊙O上一点P,过点P画⊙O的切线.
做一做
.P
.O
新知讲解
画法:
(1)连接OP,将三角尺的直角顶点放在点P处,并使 一直角边与半径OP重合;
(2)过点P沿着三角尺的另一条直角边画直线l,则l就 是所要画的切线. 如图2-40.
.O
.P
图2-40
l
新知讲解
因为画出来的直线l符合切线的定义,l经过⊙O的半径OP的外端点P,并且l⊥OP,所以直线l是⊙O的切线.
为什么画出来的直线l是⊙O的切线呢?
新知讲解
例2 如图,已知AD是⊙O的直径,直线BC经过点D,并且AB=AC,∠BAD=∠CAD.
求证:直线BC是⊙O的切线.
点拨:由于AB=AC,利用等腰三角形的性质证明AD⊥BC。即可证明BC是⊙O的切线。
新知讲解
证明:∵ AB=AC,∠BAD=∠CAD ,
∴ AD⊥BC.
又∵ OD是⊙O的半径,且BC经过点D,
∴ 直线BC是⊙O的切线.
新知讲解
切线的判定方法:
圆心到直线的距离d等于半径r
d
r
定义:直线与圆只有一个公共点A
定理判定:证明OA⊥l
A
O
l
A
新知讲解
如图,切线的判定常作的辅助线有哪些?
(1)连半径OA,证明l与半径OA垂直;
(2)作垂直OA⊥l,证明OA=r
A
1.下列四个选项中的表述,正确的是( )
A. 经过半径上一点且垂直于这条半径的直线是圆的切线
B. 经过半径的端点且垂直于这条半径的直线是圆的切线
C. 经过半径的外端且垂直于这条半径的直线是圆的切线
D. 经过一条弦的外端且垂直于这条弦的直线是圆的切线
课堂练习
C
课堂练习
解:由切线的判定定理可知:
经过半径外端点且与这条半径垂直的直线是圆的切线,
故A,B,D,选项不正确,选项C正确,
故选C.
课堂练习
2. 如图,以点P为圆心作圆,所得的圆与直线l相切的是 ( )
A. 以PA为半径的圆 B. 以PB为半径的圆
C. 以PC为半径的圆 D. 以PD为半径的圆
C
课堂练习
解:∵PC⊥l于C,
∴以点P为圆心,PC为半径的圆与直线l相切.
故选C.
课堂练习
3. 如图,AB=BC,以BC为直径作⊙O,AC交⊙O于点E,过点E作EG⊥AB于点F,交CB的延长线于点G.
求证:EG是⊙O的切线;
课堂练习
解:连接OE.∵AB=BC,∴∠A=∠C;
∵OE=OC,∴∠OEC=∠C,
∴∠A=∠OEC,∴OE//AB,
∵BA⊥GE,
∴OE⊥EG,且OE为半径;
∴EG是⊙O的切线;
课堂总结
圆的切线
1 切线的判定定理
2. 用三角尺画圆的切线
经过半径外端并且垂直于这条半径的直线是圆的切线
板书设计
2.5.2圆的切线
1.切线的判定定理;
2.用三角尺画圆的切线;
作业布置
必做题:课本67页的练习第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
