【核心素养目标】2.6弧长与扇形面积(2) 教学设计
文档属性
| 名称 | 【核心素养目标】2.6弧长与扇形面积(2) 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 15:35:50 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版版九年级下册数学2.6弧长与扇形面积(2)教学设计
课题 2.6弧长与扇形面积(2) 单元 第一单元 学科 数学 年级 九
教材分析 类比弧长公式的推导方法,推出扇形面积公式,并进行相关的计算,会利用扇形面积求圆、扇形组合的图形的面积,求组合图形面积在中考中是常考题型,以小题为主
核心素养分析 本节延续上一节的推导公式的方法,本节内容推导扇形的面积公式,考查了学生的推理能力,本节学习后,学生掌握扇形公式并计算,培养了学生的计算能力,计算能力也是中考的基本要求之一。
学习目标 1.认识扇形的概念2.类比弧长公式的推导方法,推出扇形面积公式,并进行相关的计算3.会利用扇形面积求圆、扇形等组合图形的面积
重点 类比弧长公式的推导方法,推出扇形面积公式,并进行相关的计算
难点 会利用扇形面积求圆、扇形等组合图形的面积
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 弧长公式是什么呢?圆的面积公式呢? 上式中,n是圆心角的度数,r是圆的半径S圆=πR ,其中,R是指圆的半径. 回顾知识,让学生回答,温故知新,复习圆的周长和圆的面积。 从回顾上节知识,引入新的内容,让学生开始认识圆的周长和圆的面积。
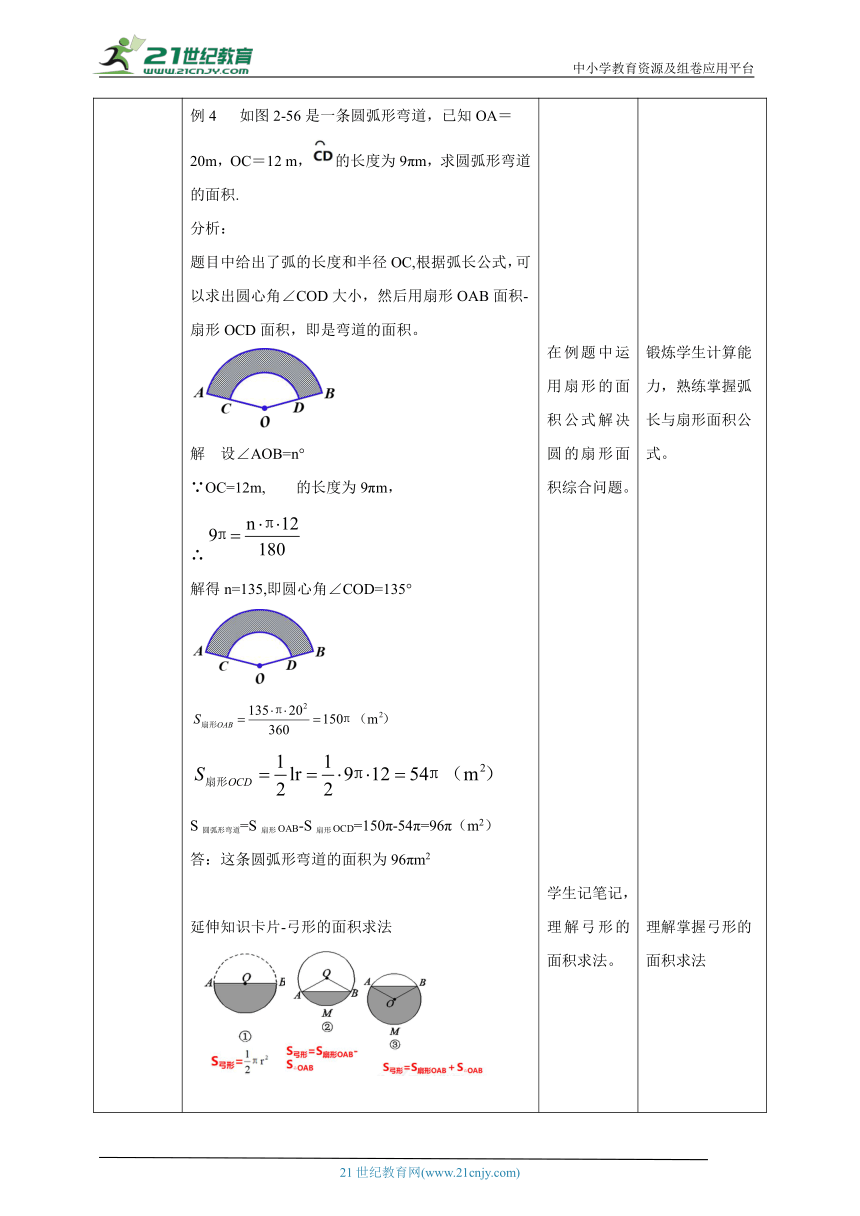
讲授新课 议一议圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.如图2-54,蓝色部分是一个扇形,记作扇形OAB.图2-54扇形面积与组成扇形的圆心角的大小有关,在同一个圆中,圆心角越大,扇形面积也越大.探究如何求半径为r, 圆心角为n°的扇形的面积呢?圆看作是圆心角为360°的扇形,圆面积S=πr2. 因为圆绕圆心旋转任意角度,都能与自身重合,所以圆心角为1°的扇形能够互相重合,从而圆心角为1°的扇形的面积等于圆面积的 ,即 . 因此,圆心角为n°的扇形的面积为半径为r的圆中,圆心角为n°的扇形的面积为扇形的面积和弧长之间有什么关系?∵扇形的弧长 例3 如图2-55,⊙O的半径为1.5cm,圆心角∠AOB=58°,求扇形OAB的面积(精确到0.1cm2). 图2-55解∵ r=1.5cm ,n=58, S扇形OAB=例4 如图2-56是一条圆弧形弯道,已知OA=20m,OC=12 m,的长度为9πm,求圆弧形弯道的面积.分析:题目中给出了弧的长度和半径OC,根据弧长公式,可以求出圆心角∠COD大小,然后用扇形OAB面积-扇形OCD面积,即是弯道的面积。解 设∠AOB=n°∵OC=12m, 的长度为9πm,∴解得n=135,即圆心角∠COD=135°S圆弧形弯道=S扇形OAB-S扇形OCD=150π-54π=96π(m2)答:这条圆弧形弯道的面积为96πm2延伸知识卡片-弓形的面积求法 学生独立思考、小组合作,探究扇形面积与组成扇形的圆心角的大小的关系。 探究扇形面积公式的推导过程,小组合作,讨论。 在例题中运用扇形的面积公式解决圆的扇形面积综合问题。学生记笔记,理解弓形的面积求法。 理解扇形面积与圆心角这个量有关系的。 锻炼学生的推理能力。 锻炼学生计算能力,熟练掌握弧长与扇形面积公式。理解掌握弓形的面积求法
课堂练习 1.如图,每个圆的半径都是1cm,则图中的三个扇形(即阴影部分)的面积之和为( )A. 3π B. C. 2π D. π解:∵∠A+∠B+∠C=180°,∴阴影部分的面积= =.故选B.2.如图是2022年杭州亚运会徽标的示意图,若AO=5,BO=2,∠AOD=120°,则阴影部分面积为( )A. 14π B. 7π C. 3 π D. 2π解:S阴影=S扇形AOD-S扇形BOC = =7π,故选:B.3.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是______.解:作DH⊥AE于H,∵∠AOB=90°,OA=3,OB=2,∴AB=,由旋转的性质可知,OE=OB=2,DE=EF=AB= ,△DHE≌△BOA,∴DH=OB=2,阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积= -=8-π, 学生做本节练习,掌握扇形的面积公式,教师进行补充,做最后总结。 练习是为了巩固学生对知识的掌握,理解运用扇形面积公式。
课堂小结 学生先发言总结,在教师的引导下总结归纳弧长公式与面积公式。 让学生自己对本节知识进行整合归纳,培养学生养成及时总结的习惯,形成自己的知识体系。
板书 课题:2.6 弧长与扇形面积(2)1.扇形面积公式2. 例题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
湘教版版九年级下册数学2.6弧长与扇形面积(2)教学设计
课题 2.6弧长与扇形面积(2) 单元 第一单元 学科 数学 年级 九
教材分析 类比弧长公式的推导方法,推出扇形面积公式,并进行相关的计算,会利用扇形面积求圆、扇形组合的图形的面积,求组合图形面积在中考中是常考题型,以小题为主
核心素养分析 本节延续上一节的推导公式的方法,本节内容推导扇形的面积公式,考查了学生的推理能力,本节学习后,学生掌握扇形公式并计算,培养了学生的计算能力,计算能力也是中考的基本要求之一。
学习目标 1.认识扇形的概念2.类比弧长公式的推导方法,推出扇形面积公式,并进行相关的计算3.会利用扇形面积求圆、扇形等组合图形的面积
重点 类比弧长公式的推导方法,推出扇形面积公式,并进行相关的计算
难点 会利用扇形面积求圆、扇形等组合图形的面积
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 弧长公式是什么呢?圆的面积公式呢? 上式中,n是圆心角的度数,r是圆的半径S圆=πR ,其中,R是指圆的半径. 回顾知识,让学生回答,温故知新,复习圆的周长和圆的面积。 从回顾上节知识,引入新的内容,让学生开始认识圆的周长和圆的面积。
讲授新课 议一议圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.如图2-54,蓝色部分是一个扇形,记作扇形OAB.图2-54扇形面积与组成扇形的圆心角的大小有关,在同一个圆中,圆心角越大,扇形面积也越大.探究如何求半径为r, 圆心角为n°的扇形的面积呢?圆看作是圆心角为360°的扇形,圆面积S=πr2. 因为圆绕圆心旋转任意角度,都能与自身重合,所以圆心角为1°的扇形能够互相重合,从而圆心角为1°的扇形的面积等于圆面积的 ,即 . 因此,圆心角为n°的扇形的面积为半径为r的圆中,圆心角为n°的扇形的面积为扇形的面积和弧长之间有什么关系?∵扇形的弧长 例3 如图2-55,⊙O的半径为1.5cm,圆心角∠AOB=58°,求扇形OAB的面积(精确到0.1cm2). 图2-55解∵ r=1.5cm ,n=58, S扇形OAB=例4 如图2-56是一条圆弧形弯道,已知OA=20m,OC=12 m,的长度为9πm,求圆弧形弯道的面积.分析:题目中给出了弧的长度和半径OC,根据弧长公式,可以求出圆心角∠COD大小,然后用扇形OAB面积-扇形OCD面积,即是弯道的面积。解 设∠AOB=n°∵OC=12m, 的长度为9πm,∴解得n=135,即圆心角∠COD=135°S圆弧形弯道=S扇形OAB-S扇形OCD=150π-54π=96π(m2)答:这条圆弧形弯道的面积为96πm2延伸知识卡片-弓形的面积求法 学生独立思考、小组合作,探究扇形面积与组成扇形的圆心角的大小的关系。 探究扇形面积公式的推导过程,小组合作,讨论。 在例题中运用扇形的面积公式解决圆的扇形面积综合问题。学生记笔记,理解弓形的面积求法。 理解扇形面积与圆心角这个量有关系的。 锻炼学生的推理能力。 锻炼学生计算能力,熟练掌握弧长与扇形面积公式。理解掌握弓形的面积求法
课堂练习 1.如图,每个圆的半径都是1cm,则图中的三个扇形(即阴影部分)的面积之和为( )A. 3π B. C. 2π D. π解:∵∠A+∠B+∠C=180°,∴阴影部分的面积= =.故选B.2.如图是2022年杭州亚运会徽标的示意图,若AO=5,BO=2,∠AOD=120°,则阴影部分面积为( )A. 14π B. 7π C. 3 π D. 2π解:S阴影=S扇形AOD-S扇形BOC = =7π,故选:B.3.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是______.解:作DH⊥AE于H,∵∠AOB=90°,OA=3,OB=2,∴AB=,由旋转的性质可知,OE=OB=2,DE=EF=AB= ,△DHE≌△BOA,∴DH=OB=2,阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积= -=8-π, 学生做本节练习,掌握扇形的面积公式,教师进行补充,做最后总结。 练习是为了巩固学生对知识的掌握,理解运用扇形面积公式。
课堂小结 学生先发言总结,在教师的引导下总结归纳弧长公式与面积公式。 让学生自己对本节知识进行整合归纳,培养学生养成及时总结的习惯,形成自己的知识体系。
板书 课题:2.6 弧长与扇形面积(2)1.扇形面积公式2. 例题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
