【新课标】2.6弧长与扇形面积(2) 课件(共32张PPT)
文档属性
| 名称 | 【新课标】2.6弧长与扇形面积(2) 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 15:38:17 | ||
图片预览









文档简介
(共32张PPT)
2.6 弧长与扇形面积(2)
湘教版 九年级下
教学内容分析
在上一节学习了弧长公式的推导方法,这一节类比方法,利用扇形占圆的比例,推出扇形面积的公式,并进行相关的计算,并求出组合图形的面积。
教学目标
1.认识扇形的概念;
2.类比弧长公式的推导方法,推出扇形面积公式,并进行相关的计算(重点)
3. 会利用扇形面积求圆、扇形等组合图形的面积(难点)
核心素养分析
本节延续上一节的推导公式的方法,本节内容是推导扇形的面积公式,考查了学生的推理能力,本节学习后,学生掌握扇形公式并计算,培养了学生的计算能力,计算能力也是中考的基本要求之一。
新知导入
弧长公式是什么呢?圆的面积公式呢?
上式中,n是圆心角的度数,r是圆的半径.
S圆=π r ,其中,R是指圆的半径.
新知讲解
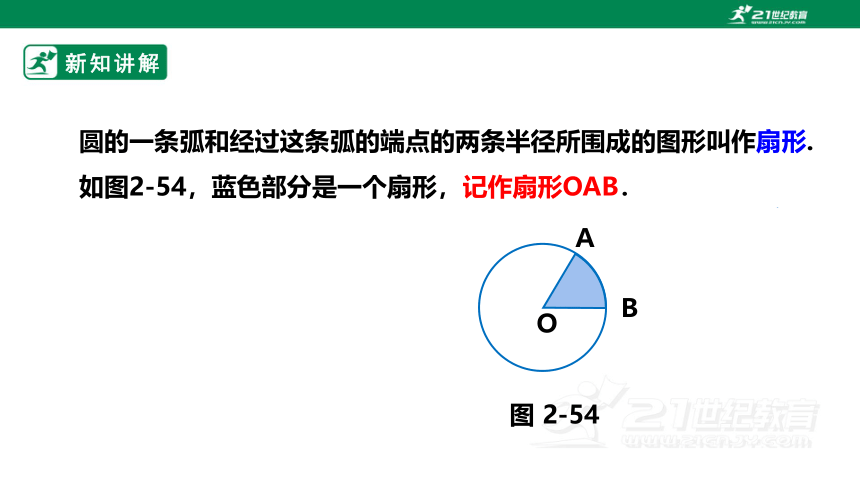
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
如图2-54,蓝色部分是一个扇形,记作扇形OAB.
B
A
O
图 2-54
新知讲解
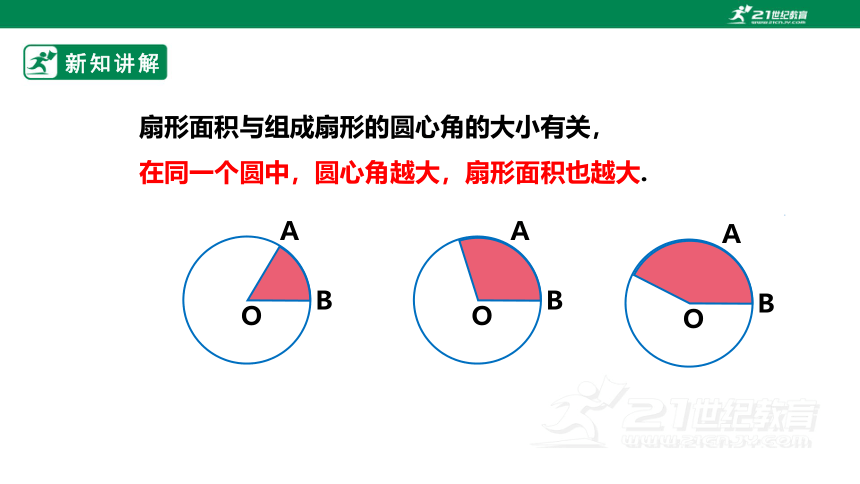
扇形面积与组成扇形的圆心角的大小有关,
在同一个圆中,圆心角越大,扇形面积也越大.
B
A
O
B
A
O
B
A
O
新知讲解
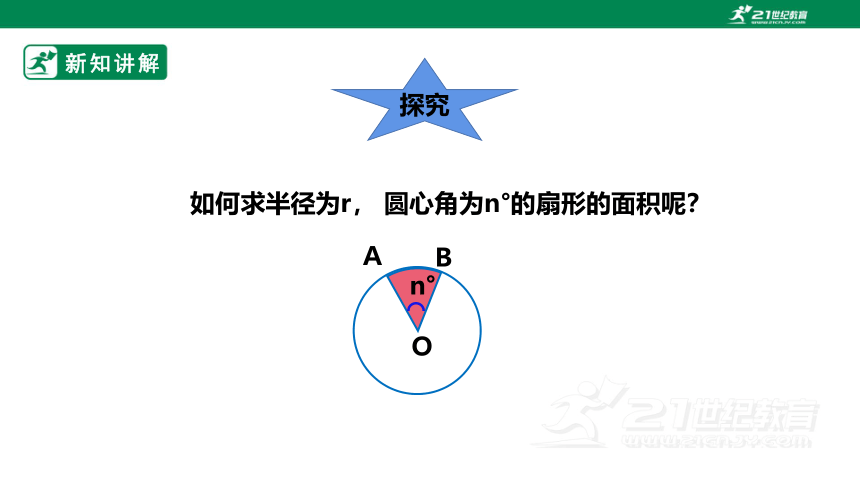
如何求半径为r, 圆心角为n°的扇形的面积呢?
探究
B
A
O
n°
⌒
新知讲解
圆看作是圆心角为360°的扇形,圆面积S=πr2.
因为圆绕圆心旋转任意角度,都能与自身重合,
所以圆心角为1°的扇形能够互相重合,
从而圆心角为1°的扇形的面积等于圆面积的 ,
即 .
因此,圆心角为n°的扇形的面积为 .
B
A
O
n°
⌒
半径为r的圆中,圆心角为n°的扇形的面积为
新知讲解
新知讲解
扇形的面积和弧长之间有什么关系?
∵扇形的弧长
∴
新知讲解
例3 如图2-55,⊙O的半径为1.5cm,圆心角∠AOB=58°,求扇形OAB的面积(精确到0.1cm2).
B
A
图2-55
O
58°
解∵ r=1.5cm ,n=58,
S扇形OAB=
变式1 如图,在 ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是( )
A. π B. 2π C. 3π D. 6π
新知讲解
C
新知讲解
解∵在 ABCD中,∠B=60°,⊙C的半径为3,
∴∠C=120°,
∴图中阴影部分的面积是: ,
故选C.
新知讲解
例4 如图2-56是一条圆弧形弯道,已知OA=20m,OC=12 m, 的长度为9πm,求圆弧形弯道的面积.
⌒
CD
图2-56
分析:
题目中给出了弧的长度和半径OC,根据弧长公式,可以求出圆心角∠COD大小,然后用扇形OAB面积-扇形OCD面积,即是弯道的面积。
新知讲解
解 设∠AOB=n°
∵OC=12m,的长度为9πm,
∴
解得n=135,即圆心角∠COD=135°
∴S圆弧形弯道=S扇形OAB-S扇形OCD=150π-54π=96π(m2)
答:这条圆弧形弯道的面积为96πm2
变式2 某排水管的截面如图,已知截面圆半径OB=10cm,水面宽AB= cm,则求弓形的面积______.
新知讲解
新知讲解
解:由题意知OD⊥AB,交AB于点C,
∵OB=10cm,AB= cm
∴BC=
在Rt△OCB中,
∴
∴OB=2OC,
∴∠OBC=30°
∴∠COB=60°
连接AO
∴∠AOB=120°
S弓形=S扇形AOB-S△AOB
=
新知讲解
-------
新知讲解
延伸知识卡片-弓形的面积求法
S弓形=S扇形OAB-S△OAB
S弓形=
S弓形=S扇形OAB+S△OAB
1.如图,每个圆的半径都是1cm,则图中的三个扇形(即阴影部分)的面积之和为( )
A. 3π B. C. 2π D. π
课堂练习
B
课堂练习
解:∵∠A+∠B+∠C=180°,
∴阴影部分的面积= = .
故选B.
课堂练习
2.如图是2022年杭州亚运会徽标的示意图,若AO=5,BO=2,∠AOD=120°,则阴影部分面积为( )
A. 14π B. 7π C. 3 π D. 2π
B
课堂练习
解:S阴影=S扇形AOD-S扇形BOC
=
=7π,
故选:B.
课堂练习
3.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是______.
8-π
课堂练习
解:作DH⊥AE于H,
∵∠AOB=90°,OA=3,OB=2,
∴AB= ,
由旋转的性质可知,
OE=OB=2,DE=EF=AB= ,
△DHE≌△BOA,
∴DH=OB=2,
课堂练习
阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积
= -
=8-π,
课堂总结
扇形面积
公式
2公式
1扇形面积公式的推导
板书设计
2.6 弧长与扇形面积(2)
1.扇形面积公式
2. 例题
作业布置
必做题:课本80页的练习第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.6 弧长与扇形面积(2)
湘教版 九年级下
教学内容分析
在上一节学习了弧长公式的推导方法,这一节类比方法,利用扇形占圆的比例,推出扇形面积的公式,并进行相关的计算,并求出组合图形的面积。
教学目标
1.认识扇形的概念;
2.类比弧长公式的推导方法,推出扇形面积公式,并进行相关的计算(重点)
3. 会利用扇形面积求圆、扇形等组合图形的面积(难点)
核心素养分析
本节延续上一节的推导公式的方法,本节内容是推导扇形的面积公式,考查了学生的推理能力,本节学习后,学生掌握扇形公式并计算,培养了学生的计算能力,计算能力也是中考的基本要求之一。
新知导入
弧长公式是什么呢?圆的面积公式呢?
上式中,n是圆心角的度数,r是圆的半径.
S圆=π r ,其中,R是指圆的半径.
新知讲解
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
如图2-54,蓝色部分是一个扇形,记作扇形OAB.
B
A
O
图 2-54
新知讲解
扇形面积与组成扇形的圆心角的大小有关,
在同一个圆中,圆心角越大,扇形面积也越大.
B
A
O
B
A
O
B
A
O
新知讲解
如何求半径为r, 圆心角为n°的扇形的面积呢?
探究
B
A
O
n°
⌒
新知讲解
圆看作是圆心角为360°的扇形,圆面积S=πr2.
因为圆绕圆心旋转任意角度,都能与自身重合,
所以圆心角为1°的扇形能够互相重合,
从而圆心角为1°的扇形的面积等于圆面积的 ,
即 .
因此,圆心角为n°的扇形的面积为 .
B
A
O
n°
⌒
半径为r的圆中,圆心角为n°的扇形的面积为
新知讲解
新知讲解
扇形的面积和弧长之间有什么关系?
∵扇形的弧长
∴
新知讲解
例3 如图2-55,⊙O的半径为1.5cm,圆心角∠AOB=58°,求扇形OAB的面积(精确到0.1cm2).
B
A
图2-55
O
58°
解∵ r=1.5cm ,n=58,
S扇形OAB=
变式1 如图,在 ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是( )
A. π B. 2π C. 3π D. 6π
新知讲解
C
新知讲解
解∵在 ABCD中,∠B=60°,⊙C的半径为3,
∴∠C=120°,
∴图中阴影部分的面积是: ,
故选C.
新知讲解
例4 如图2-56是一条圆弧形弯道,已知OA=20m,OC=12 m, 的长度为9πm,求圆弧形弯道的面积.
⌒
CD
图2-56
分析:
题目中给出了弧的长度和半径OC,根据弧长公式,可以求出圆心角∠COD大小,然后用扇形OAB面积-扇形OCD面积,即是弯道的面积。
新知讲解
解 设∠AOB=n°
∵OC=12m,的长度为9πm,
∴
解得n=135,即圆心角∠COD=135°
∴S圆弧形弯道=S扇形OAB-S扇形OCD=150π-54π=96π(m2)
答:这条圆弧形弯道的面积为96πm2
变式2 某排水管的截面如图,已知截面圆半径OB=10cm,水面宽AB= cm,则求弓形的面积______.
新知讲解
新知讲解
解:由题意知OD⊥AB,交AB于点C,
∵OB=10cm,AB= cm
∴BC=
在Rt△OCB中,
∴
∴OB=2OC,
∴∠OBC=30°
∴∠COB=60°
连接AO
∴∠AOB=120°
S弓形=S扇形AOB-S△AOB
=
新知讲解
-------
新知讲解
延伸知识卡片-弓形的面积求法
S弓形=S扇形OAB-S△OAB
S弓形=
S弓形=S扇形OAB+S△OAB
1.如图,每个圆的半径都是1cm,则图中的三个扇形(即阴影部分)的面积之和为( )
A. 3π B. C. 2π D. π
课堂练习
B
课堂练习
解:∵∠A+∠B+∠C=180°,
∴阴影部分的面积= = .
故选B.
课堂练习
2.如图是2022年杭州亚运会徽标的示意图,若AO=5,BO=2,∠AOD=120°,则阴影部分面积为( )
A. 14π B. 7π C. 3 π D. 2π
B
课堂练习
解:S阴影=S扇形AOD-S扇形BOC
=
=7π,
故选:B.
课堂练习
3.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是______.
8-π
课堂练习
解:作DH⊥AE于H,
∵∠AOB=90°,OA=3,OB=2,
∴AB= ,
由旋转的性质可知,
OE=OB=2,DE=EF=AB= ,
△DHE≌△BOA,
∴DH=OB=2,
课堂练习
阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积
= -
=8-π,
课堂总结
扇形面积
公式
2公式
1扇形面积公式的推导
板书设计
2.6 弧长与扇形面积(2)
1.扇形面积公式
2. 例题
作业布置
必做题:课本80页的练习第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
