【核心素养目标】2.7正多边形与圆 教学设计
文档属性
| 名称 | 【核心素养目标】2.7正多边形与圆 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版版九年级下册数学2.7正多边形与圆 教学设计
课题 2.7正多边形与圆 单元 第一单元 学科 数学 年级 九
教材分析 在前面学习了圆内接的四边形,本节继续研究正多边形,以及它们的外接圆,并总结出正多边形的性质,来解决圆与正多边形的问题。
核心素养分析 本节课探讨了正多边形以及它们的外接圆之间的关系,培养了学生几何直观的素养,还会总结出正多边形的性质,利用这些性质来解决圆与正多边形的综合问题,塑造了学生科学严谨的推理能力。
学习目标 1. 熟悉正n边形、圆的内接正多边形等概念 2. 掌握用量角器将圆心角等分的方法作圆的内接正多边形;3. 掌握内接正多边形的对称性,并解决圆与正多边形的问题。
重点 熟悉正n边形、圆的内接正多边形等概念
难点 掌握内接正多边形的对称性,并解决圆与正多边形的问题。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 下列图形哪些是轴对称图形,哪些是中心对称图形?圆,等边三角形,正方形,正五边形,正六边形轴对称图形:圆,等边三角形,正方形,正五边形,正六边形中心对称图形:圆,正方形,正六边形。 回顾知识,让学生回答,温故知新,复习圆与正多边形的对称性。 从回顾上节知识,引入新的内容,圆与正多边形。
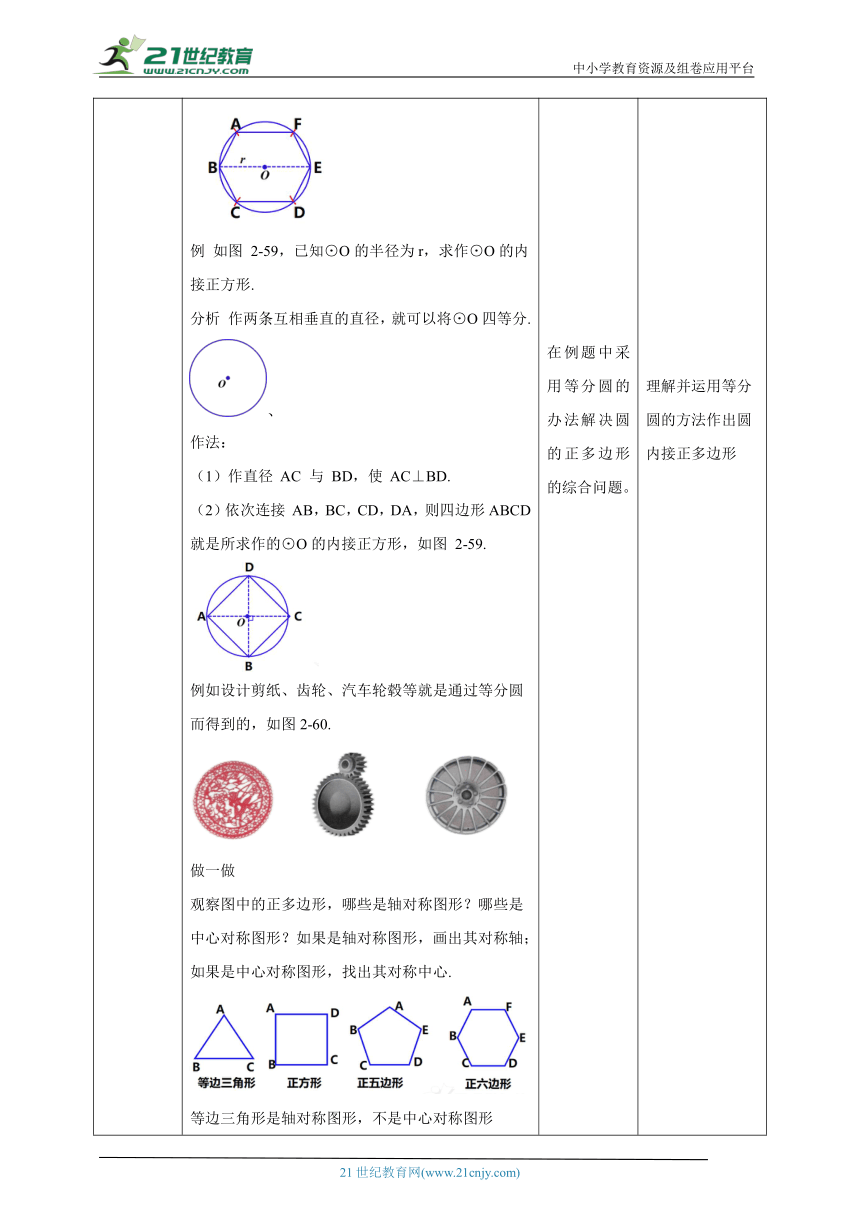
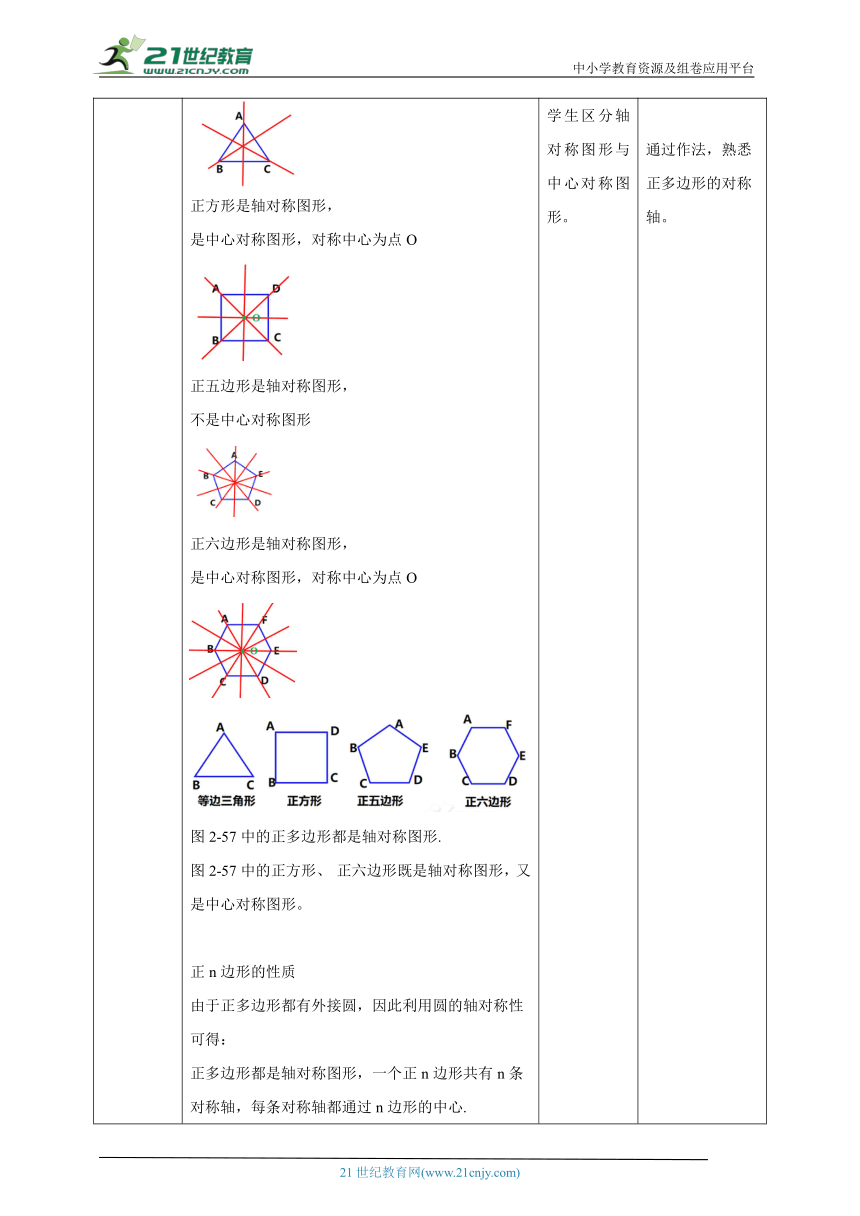
讲授新课 说一说如图2-57, 这些多边形有什么共同的特点?每个多边形的各边都相等, 各内角也相等我们把各边相等, 各内角也相等的多边形叫作正多边形。n边形的各边相等,各内角也相等,我们就说这个n边形是正n边形.如何作一个正多边形呢?由于在同圆中,相等的圆心角所对的弧相等,所对的弦也相等,因此可以用量角器将圆心角n等分,从而使圆n等分,依次连接各等分点,可得到一个正n边形.将一个圆n(n≥3)等分,依次连接各等分点所得的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆,正多边形的外接圆的圆心叫作正多边形的中心.做一做已知⊙O 的半径为r, 求作⊙O的内接正六边形.因为正六边形的每条边所对的圆心角为60°,所以正六边形的边长与圆的半径相等。因此在半径为r的圆上依次截取等于半径r的弦,就可以将圆六等分.作法:(1)作圆的直径BE,分别以B,E为圆心,以r为半径作弧,与⊙O分别交于点A,C和F,D.(2)依次连接AB,BC,CD,DE,EF,FA,则六边形ABCDEF就是所求作的⊙O的内接正六边形例 如图 2-59,已知⊙O的半径为r,求作⊙O的内接正方形. 分析 作两条互相垂直的直径,就可以将⊙O四等分.、作法: (1)作直径 AC 与 BD,使 AC⊥BD. (2)依次连接 AB,BC,CD,DA,则四边形ABCD就是所求作的⊙O的内接正方形,如图 2-59.例如设计剪纸、齿轮、汽车轮毂等就是通过等分圆而得到的,如图2-60.做一做观察图中的正多边形,哪些是轴对称图形?哪些是中心对称图形?如果是轴对称图形,画出其对称轴;如果是中心对称图形,找出其对称中心.等边三角形是轴对称图形,不是中心对称图形正方形是轴对称图形,是中心对称图形,对称中心为点O正五边形是轴对称图形,不是中心对称图形正六边形是轴对称图形,是中心对称图形,对称中心为点O图2-57中的正多边形都是轴对称图形.图2-57中的正方形、 正六边形既是轴对称图形,又是中心对称图形。正n边形的性质由于正多边形都有外接圆,因此利用圆的轴对称性可得:正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心.n为奇数时,正n边形的n条对称轴都是顶点与中心的连线;当n为偶数时,有条对称轴都是顶点与中心的连线,有条对称轴是过中心与边垂直的直线.利用圆绕圆心旋转任意角度,所得图形都与自身重合这一性质可以得出:一个正n边形,绕它的中心旋转所得图形与这个正n边形重合。当n为偶数时,正n边形绕它的中心旋转,所得图形与这个正n边形重合. 因此正n边形(n为偶数)也是中心对称图形,它的对称中心就是这个正n边形的中心.延伸如图六边形ABCDEF是圆O的内接正六边形连接OB、OC、OD,则∠BOC,∠ COD是中心角;过点O作OM⊥CD,垂足为M,OM是这个正六边形的边心距。 学生独立思考、小组合作,认识正多边形的概念,探究作出一个圆内接的正多边形。 学生按照作法进行操作,作出⊙O的内接正六边形 在例题中采用等分圆的办法解决圆的正多边形的综合问题。学生区分轴对称图形与中心对称图形。正n边形的性质,从对称性,对称轴的角度去理解。 学生理解概念,判断正多边形,作出图形,锻炼学生动手能力。 动手操作后,可以加深对正多边形的理解。 理解并运用等分圆的方法作出圆内接正多边形通过作法,熟悉正多边形的对称轴。 学会性质,并熟练应用性质解题。
课堂练习 1.若正六边形外接圆的半径为4,则它的边长为( )A. 2 B. 3 C. 4 D. 5 解:正六边形的中心角为360°÷6=60°,那么外接圆的半径和正六边形的边长将组成一个等边三角形,故正六边形的外接圆半径等于4,则正六边形的边长是4.故选:C.2.如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形OM的边心距长为 ( ) A. 2 B. C. 3 D. 4解:如图,连接OB,OC,因为多边形ABCDEF是正六边形,所以∠BOC=60°,因为OB=OC,所以△BOC是等边三角形,所以∠OBM=60°,∠BOM=30°,所以BM=OB=2,所以在Rt△OBM中,由勾股定理得OM= 故选B.3. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=________.解: 连结OA,∵五边形ABCDE是正五边形,∴∠AOB=360°÷5=72°,∵△AMN是正三角形,∴∠AOM=360÷3=120°,∴∠BOM=∠AOM-∠AOB=48°.故答案为:48°. 学生做本节练习,掌握圆内接正多边形的性质,教师进行补充,做最后总结。 练习是为了巩固学生对知识的掌握,理解运用圆内接正多边形的性质。
课堂小结 学生先发言总结,在教师的引导下总结归纳圆内接正多边形的性质。 让学生自己对本节知识进行整合归纳,培养学生养成及时总结的习惯,形成自己的知识体系。
板书 课题:2.7 正多边形与圆基本概念2. 等分圆作出圆内接正多边形;3. 圆内接正多边形性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
湘教版版九年级下册数学2.7正多边形与圆 教学设计
课题 2.7正多边形与圆 单元 第一单元 学科 数学 年级 九
教材分析 在前面学习了圆内接的四边形,本节继续研究正多边形,以及它们的外接圆,并总结出正多边形的性质,来解决圆与正多边形的问题。
核心素养分析 本节课探讨了正多边形以及它们的外接圆之间的关系,培养了学生几何直观的素养,还会总结出正多边形的性质,利用这些性质来解决圆与正多边形的综合问题,塑造了学生科学严谨的推理能力。
学习目标 1. 熟悉正n边形、圆的内接正多边形等概念 2. 掌握用量角器将圆心角等分的方法作圆的内接正多边形;3. 掌握内接正多边形的对称性,并解决圆与正多边形的问题。
重点 熟悉正n边形、圆的内接正多边形等概念
难点 掌握内接正多边形的对称性,并解决圆与正多边形的问题。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 下列图形哪些是轴对称图形,哪些是中心对称图形?圆,等边三角形,正方形,正五边形,正六边形轴对称图形:圆,等边三角形,正方形,正五边形,正六边形中心对称图形:圆,正方形,正六边形。 回顾知识,让学生回答,温故知新,复习圆与正多边形的对称性。 从回顾上节知识,引入新的内容,圆与正多边形。
讲授新课 说一说如图2-57, 这些多边形有什么共同的特点?每个多边形的各边都相等, 各内角也相等我们把各边相等, 各内角也相等的多边形叫作正多边形。n边形的各边相等,各内角也相等,我们就说这个n边形是正n边形.如何作一个正多边形呢?由于在同圆中,相等的圆心角所对的弧相等,所对的弦也相等,因此可以用量角器将圆心角n等分,从而使圆n等分,依次连接各等分点,可得到一个正n边形.将一个圆n(n≥3)等分,依次连接各等分点所得的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆,正多边形的外接圆的圆心叫作正多边形的中心.做一做已知⊙O 的半径为r, 求作⊙O的内接正六边形.因为正六边形的每条边所对的圆心角为60°,所以正六边形的边长与圆的半径相等。因此在半径为r的圆上依次截取等于半径r的弦,就可以将圆六等分.作法:(1)作圆的直径BE,分别以B,E为圆心,以r为半径作弧,与⊙O分别交于点A,C和F,D.(2)依次连接AB,BC,CD,DE,EF,FA,则六边形ABCDEF就是所求作的⊙O的内接正六边形例 如图 2-59,已知⊙O的半径为r,求作⊙O的内接正方形. 分析 作两条互相垂直的直径,就可以将⊙O四等分.、作法: (1)作直径 AC 与 BD,使 AC⊥BD. (2)依次连接 AB,BC,CD,DA,则四边形ABCD就是所求作的⊙O的内接正方形,如图 2-59.例如设计剪纸、齿轮、汽车轮毂等就是通过等分圆而得到的,如图2-60.做一做观察图中的正多边形,哪些是轴对称图形?哪些是中心对称图形?如果是轴对称图形,画出其对称轴;如果是中心对称图形,找出其对称中心.等边三角形是轴对称图形,不是中心对称图形正方形是轴对称图形,是中心对称图形,对称中心为点O正五边形是轴对称图形,不是中心对称图形正六边形是轴对称图形,是中心对称图形,对称中心为点O图2-57中的正多边形都是轴对称图形.图2-57中的正方形、 正六边形既是轴对称图形,又是中心对称图形。正n边形的性质由于正多边形都有外接圆,因此利用圆的轴对称性可得:正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心.n为奇数时,正n边形的n条对称轴都是顶点与中心的连线;当n为偶数时,有条对称轴都是顶点与中心的连线,有条对称轴是过中心与边垂直的直线.利用圆绕圆心旋转任意角度,所得图形都与自身重合这一性质可以得出:一个正n边形,绕它的中心旋转所得图形与这个正n边形重合。当n为偶数时,正n边形绕它的中心旋转,所得图形与这个正n边形重合. 因此正n边形(n为偶数)也是中心对称图形,它的对称中心就是这个正n边形的中心.延伸如图六边形ABCDEF是圆O的内接正六边形连接OB、OC、OD,则∠BOC,∠ COD是中心角;过点O作OM⊥CD,垂足为M,OM是这个正六边形的边心距。 学生独立思考、小组合作,认识正多边形的概念,探究作出一个圆内接的正多边形。 学生按照作法进行操作,作出⊙O的内接正六边形 在例题中采用等分圆的办法解决圆的正多边形的综合问题。学生区分轴对称图形与中心对称图形。正n边形的性质,从对称性,对称轴的角度去理解。 学生理解概念,判断正多边形,作出图形,锻炼学生动手能力。 动手操作后,可以加深对正多边形的理解。 理解并运用等分圆的方法作出圆内接正多边形通过作法,熟悉正多边形的对称轴。 学会性质,并熟练应用性质解题。
课堂练习 1.若正六边形外接圆的半径为4,则它的边长为( )A. 2 B. 3 C. 4 D. 5 解:正六边形的中心角为360°÷6=60°,那么外接圆的半径和正六边形的边长将组成一个等边三角形,故正六边形的外接圆半径等于4,则正六边形的边长是4.故选:C.2.如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形OM的边心距长为 ( ) A. 2 B. C. 3 D. 4解:如图,连接OB,OC,因为多边形ABCDEF是正六边形,所以∠BOC=60°,因为OB=OC,所以△BOC是等边三角形,所以∠OBM=60°,∠BOM=30°,所以BM=OB=2,所以在Rt△OBM中,由勾股定理得OM= 故选B.3. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=________.解: 连结OA,∵五边形ABCDE是正五边形,∴∠AOB=360°÷5=72°,∵△AMN是正三角形,∴∠AOM=360÷3=120°,∴∠BOM=∠AOM-∠AOB=48°.故答案为:48°. 学生做本节练习,掌握圆内接正多边形的性质,教师进行补充,做最后总结。 练习是为了巩固学生对知识的掌握,理解运用圆内接正多边形的性质。
课堂小结 学生先发言总结,在教师的引导下总结归纳圆内接正多边形的性质。 让学生自己对本节知识进行整合归纳,培养学生养成及时总结的习惯,形成自己的知识体系。
板书 课题:2.7 正多边形与圆基本概念2. 等分圆作出圆内接正多边形;3. 圆内接正多边形性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
