【核心素养分析】24.7.1弧长与扇形面积 教学设计
文档属性
| 名称 | 【核心素养分析】24.7.1弧长与扇形面积 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
沪科版九年级下册数学24.7.1弧长与扇形面积 教学设计
课题 24.7.1弧长与扇形面积 单元 第24单元 学科 数学 年级 九
教材分析 本节在学习了圆的概念后,根据弧长占圆的周长的比例,推导圆的弧长公式,同时根据扇形占圆的比例,推导出扇形面积的公式,根据扇形、三角形、四边形面积公式求出组合图形的阴影面积。
核心素养分析 掌握弧长占圆的周长的比例,推导圆的弧长公式,并推导圆的扇形面积公式,考查了学生的推理能力,学生掌握弧长与扇形面积的公式,并进行计算,培养了学生的计算能力,中考重点考查了求阴影部分的面积,其中含有扇形面积的计算。
学习目标 1.掌握弧长占圆的周长的比例,推导圆的弧长公式;2.推导和掌握扇形面积公式,并进行相关的计算;3.会利用扇形面积求三角形、四边形、圆、扇形等组合图形的面积。
重点 掌握弧长占圆的周长的比例,推导圆的弧长公式;推导和掌握扇形面积公式,并进行相关的计算;
难点 利用扇形面积求三角形、四边形、圆、扇形等组合图形的面积
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 如何计算下图的弯道长度? 学生观察图片,思考问题,培养学生思考问题的好习惯. 问题导入本节新课,激发学生的兴趣,学习弧长和扇形面积。
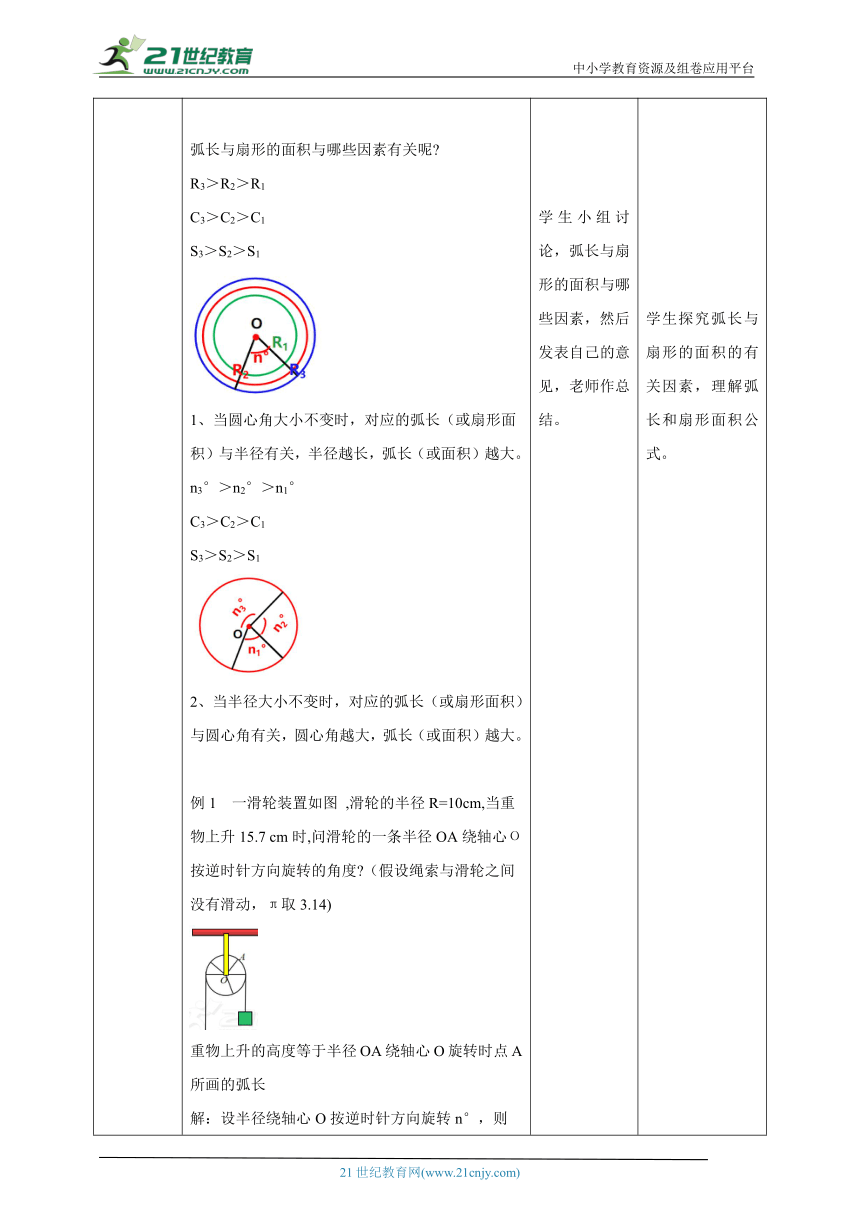
讲授新课 圆的面积公式?圆的周长公式是什么?π=3.14159......是无理数,叫做圆周率我们把两条半径与所夹弧围成的图形叫做扇形(图24-62中劣弧AB所围红色的部分或优弧AB所围白色部分).图24-62下列哪些图形是扇形吗?扇形必须满足:两条半径所夹弧围成的图形思考探究:如何求扇形的弧长和面积?在圆中,如果圆心角∠AOB=n°,那么它是周角(360°) 的.因此,n°的圆心角所对的弧长和以n°为圆心角的扇形面积分别是整个圆的周长和面积的。 弧长C1计算方法:(1)1 的圆心角所对的弧长 C1 是:(2)30 的圆心角所对的弧长C1是: (3)60 的圆心角所对的弧长C1是:(4)180 的圆心角所对的弧长 C1是:(5)n 的圆心角所对的弧长 C1是:扇形面积S1的计算方法:(1)1 的圆心角的扇形面积S1 是:(2)30 的圆心角的扇形面积S1是:(3)60 的圆心角的扇形面积S1 是:(4)180 的圆心角的扇形面积S1 是:(5)n 的圆心角的扇形面积S1 是:总结:n°的圆心角所对的弧长C1n°为圆心角的扇形面积S1注意: 用公式进行计算时,要注意公式中n的意义。 n表示1°圆心角的倍数,它是不带单位的。弧长与扇形的面积与哪些因素有关呢 R3>R2>R1C3>C2>C1S3>S2>S11、当圆心角大小不变时,对应的弧长(或扇形面积)与半径有关,半径越长,弧长(或面积)越大。n3°>n2°>n1°C3>C2>C1S3>S2>S12、当半径大小不变时,对应的弧长(或扇形面积)与圆心角有关,圆心角越大,弧长(或面积)越大。例1 一滑轮装置如图 ,滑轮的半径R=10cm,当重物上升15.7 cm时,问滑轮的一条半径OA绕轴心О按逆时针方向旋转的角度 (假设绳索与滑轮之间没有滑动,π取3.14) 重物上升的高度等于半径OA绕轴心O旋转时点A所画的弧长解:设半径绕轴心O按逆时针方向旋转n°,则解方程,得n≈90.答:滑轮按逆时针方向旋转的角度约为90°.例 古希腊埃拉托塞尼曾给出一个估算地球周长(或子午圈长)的简单方法. 如图,点S和点A分别表示埃及的赛伊尼和亚历山大两地,亚历山大在塞伊尼的北方,两地的经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5 m). 当太阳光线在赛伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为α.实际测得α是7.2°,由此估算出了地球的周长,你能进行计算吗?解 因为太阳光线可看作平行的,所以圆心角∠AOS=α=7.2°.设地球的周长(即⊙O的周长)为C,则 =250000(希腊里)≈39 625(km).答:地球的周长约为39625km. 学生理解扇形的概念。 学生理解n°为圆心角的扇形面积分别是整个圆的周长和面积的 学生通过类比的方法,推导出n 的圆心角所对的弧长公式,总结出弧长公式,并记忆。学生通过类比的方法,推导n 的圆心角的扇形面积公式,并记忆。学生小组讨论,弧长与扇形的面积与哪些因素,然后发表自己的意见,老师作总结。学生学会运用扇形和弧长公式解决实际问题。 知道扇形是圆的一部分,理解扇形占圆的一部分。 通过n°为圆心角的扇形所占的比例,推算弧长和面积公式。 锻炼学生的推理能力,找出规律,理解弧长公式中每个字母的含义。让学生体会从特殊到一般,从具体到抽象的学习方法。学生探究弧长与扇形的面积的有关因素,理解弧长和扇形面积公式。锻炼学会运用扇形和弧长公式来解决问题的能力。
课堂练习 1.如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A'OB',则A点运动的路径 的长为 ( )A. π B. 2π C. 4π D. 8π解:∵每个小正方形的边长都为1,∴OA=4,∵将△AOB绕点O顺时针旋转90°得到△A'OB',∴∠AOA'=90° ,∴A点运动的路径 的长为: 2.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则的长为( )A. 2π B. 4π C. 3π D. 解::::7:11,
,
,,.
.
,,
.
.
的长是,
故选:. 3.如图,四边形是菱形,,,扇形的半径为,圆心角为,则图中阴影部分的面积是( )
A. B. C. D. 解:如图,连接,
设,相交于点,,相交于点,
四边形是菱形,,
是等边三角形,,
,
,
的高为,
扇形的半径为,圆心角为,
,
又,
,
在和中,
,
,
.
故选A.
学生熟练运用本节扇形弧长和面积公式,互相补充,教师订正答案,最后总结正多边形与圆的性质。 练习是为了巩固学生所学的新知,教会学生运用扇形弧长和面积公式解决问题。
课堂小结 n°的圆心角所对的弧长C1n°为圆心角的扇形面积S1 学生先发言总结本节弧长公式与扇形面积公式,在教师的引导下总结归纳。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题:24.7.1 弧长与扇形面积1.弧长公式2.扇形面积公式
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
沪科版九年级下册数学24.7.1弧长与扇形面积 教学设计
课题 24.7.1弧长与扇形面积 单元 第24单元 学科 数学 年级 九
教材分析 本节在学习了圆的概念后,根据弧长占圆的周长的比例,推导圆的弧长公式,同时根据扇形占圆的比例,推导出扇形面积的公式,根据扇形、三角形、四边形面积公式求出组合图形的阴影面积。
核心素养分析 掌握弧长占圆的周长的比例,推导圆的弧长公式,并推导圆的扇形面积公式,考查了学生的推理能力,学生掌握弧长与扇形面积的公式,并进行计算,培养了学生的计算能力,中考重点考查了求阴影部分的面积,其中含有扇形面积的计算。
学习目标 1.掌握弧长占圆的周长的比例,推导圆的弧长公式;2.推导和掌握扇形面积公式,并进行相关的计算;3.会利用扇形面积求三角形、四边形、圆、扇形等组合图形的面积。
重点 掌握弧长占圆的周长的比例,推导圆的弧长公式;推导和掌握扇形面积公式,并进行相关的计算;
难点 利用扇形面积求三角形、四边形、圆、扇形等组合图形的面积
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 如何计算下图的弯道长度? 学生观察图片,思考问题,培养学生思考问题的好习惯. 问题导入本节新课,激发学生的兴趣,学习弧长和扇形面积。
讲授新课 圆的面积公式?圆的周长公式是什么?π=3.14159......是无理数,叫做圆周率我们把两条半径与所夹弧围成的图形叫做扇形(图24-62中劣弧AB所围红色的部分或优弧AB所围白色部分).图24-62下列哪些图形是扇形吗?扇形必须满足:两条半径所夹弧围成的图形思考探究:如何求扇形的弧长和面积?在圆中,如果圆心角∠AOB=n°,那么它是周角(360°) 的.因此,n°的圆心角所对的弧长和以n°为圆心角的扇形面积分别是整个圆的周长和面积的。 弧长C1计算方法:(1)1 的圆心角所对的弧长 C1 是:(2)30 的圆心角所对的弧长C1是: (3)60 的圆心角所对的弧长C1是:(4)180 的圆心角所对的弧长 C1是:(5)n 的圆心角所对的弧长 C1是:扇形面积S1的计算方法:(1)1 的圆心角的扇形面积S1 是:(2)30 的圆心角的扇形面积S1是:(3)60 的圆心角的扇形面积S1 是:(4)180 的圆心角的扇形面积S1 是:(5)n 的圆心角的扇形面积S1 是:总结:n°的圆心角所对的弧长C1n°为圆心角的扇形面积S1注意: 用公式进行计算时,要注意公式中n的意义。 n表示1°圆心角的倍数,它是不带单位的。弧长与扇形的面积与哪些因素有关呢 R3>R2>R1C3>C2>C1S3>S2>S11、当圆心角大小不变时,对应的弧长(或扇形面积)与半径有关,半径越长,弧长(或面积)越大。n3°>n2°>n1°C3>C2>C1S3>S2>S12、当半径大小不变时,对应的弧长(或扇形面积)与圆心角有关,圆心角越大,弧长(或面积)越大。例1 一滑轮装置如图 ,滑轮的半径R=10cm,当重物上升15.7 cm时,问滑轮的一条半径OA绕轴心О按逆时针方向旋转的角度 (假设绳索与滑轮之间没有滑动,π取3.14) 重物上升的高度等于半径OA绕轴心O旋转时点A所画的弧长解:设半径绕轴心O按逆时针方向旋转n°,则解方程,得n≈90.答:滑轮按逆时针方向旋转的角度约为90°.例 古希腊埃拉托塞尼曾给出一个估算地球周长(或子午圈长)的简单方法. 如图,点S和点A分别表示埃及的赛伊尼和亚历山大两地,亚历山大在塞伊尼的北方,两地的经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5 m). 当太阳光线在赛伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为α.实际测得α是7.2°,由此估算出了地球的周长,你能进行计算吗?解 因为太阳光线可看作平行的,所以圆心角∠AOS=α=7.2°.设地球的周长(即⊙O的周长)为C,则 =250000(希腊里)≈39 625(km).答:地球的周长约为39625km. 学生理解扇形的概念。 学生理解n°为圆心角的扇形面积分别是整个圆的周长和面积的 学生通过类比的方法,推导出n 的圆心角所对的弧长公式,总结出弧长公式,并记忆。学生通过类比的方法,推导n 的圆心角的扇形面积公式,并记忆。学生小组讨论,弧长与扇形的面积与哪些因素,然后发表自己的意见,老师作总结。学生学会运用扇形和弧长公式解决实际问题。 知道扇形是圆的一部分,理解扇形占圆的一部分。 通过n°为圆心角的扇形所占的比例,推算弧长和面积公式。 锻炼学生的推理能力,找出规律,理解弧长公式中每个字母的含义。让学生体会从特殊到一般,从具体到抽象的学习方法。学生探究弧长与扇形的面积的有关因素,理解弧长和扇形面积公式。锻炼学会运用扇形和弧长公式来解决问题的能力。
课堂练习 1.如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A'OB',则A点运动的路径 的长为 ( )A. π B. 2π C. 4π D. 8π解:∵每个小正方形的边长都为1,∴OA=4,∵将△AOB绕点O顺时针旋转90°得到△A'OB',∴∠AOA'=90° ,∴A点运动的路径 的长为: 2.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则的长为( )A. 2π B. 4π C. 3π D. 解::::7:11,
,
,,.
.
,,
.
.
的长是,
故选:. 3.如图,四边形是菱形,,,扇形的半径为,圆心角为,则图中阴影部分的面积是( )
A. B. C. D. 解:如图,连接,
设,相交于点,,相交于点,
四边形是菱形,,
是等边三角形,,
,
,
的高为,
扇形的半径为,圆心角为,
,
又,
,
在和中,
,
,
.
故选A.
学生熟练运用本节扇形弧长和面积公式,互相补充,教师订正答案,最后总结正多边形与圆的性质。 练习是为了巩固学生所学的新知,教会学生运用扇形弧长和面积公式解决问题。
课堂小结 n°的圆心角所对的弧长C1n°为圆心角的扇形面积S1 学生先发言总结本节弧长公式与扇形面积公式,在教师的引导下总结归纳。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题:24.7.1 弧长与扇形面积1.弧长公式2.扇形面积公式
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
