【新课标】24.7.1弧长与扇形面积 课件(共34张PPT)
文档属性
| 名称 | 【新课标】24.7.1弧长与扇形面积 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 15:53:28 | ||
图片预览







文档简介
(共34张PPT)
24.7.1 弧长与扇形面积
沪科版 九年级下
教学内容分析
本节在学习了圆的概念后,根据弧长占圆的周长的比例,推导圆的弧长公式,同时根据扇形占圆的比例,推导出扇形面积的公式,根据扇形、三角形、四边形面积公式求出组合图形的阴影面积。
教学目标
1.掌握弧长占圆的周长的比例,推导圆的弧长公式(重点)
2.推导和掌握扇形面积公式,并进行相关的计算(重点)
3.会利用扇形面积求三角形、四边形、圆、扇形等组合图形的面积(难点)
核心素养分析
掌握弧长占圆的周长的比例,推导圆的弧长公式,并推导圆的扇形面积公式,考查了学生的推理能力,学生掌握弧长与扇形面积的公式,并进行计算,培养了学生的计算能力,中考重点考查了求阴影部分的面积,其中含有扇形面积的计算。
新知导入
如何计算下图的弯道长度?
新知讲解
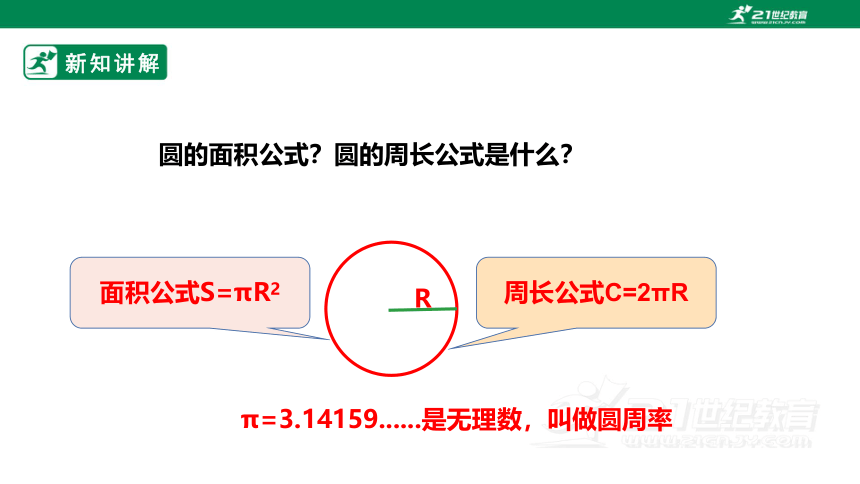
圆的面积公式?圆的周长公式是什么?
周长公式C=2πR
面积公式S=πR2
R
π=3.14159......是无理数,叫做圆周率
新知讲解
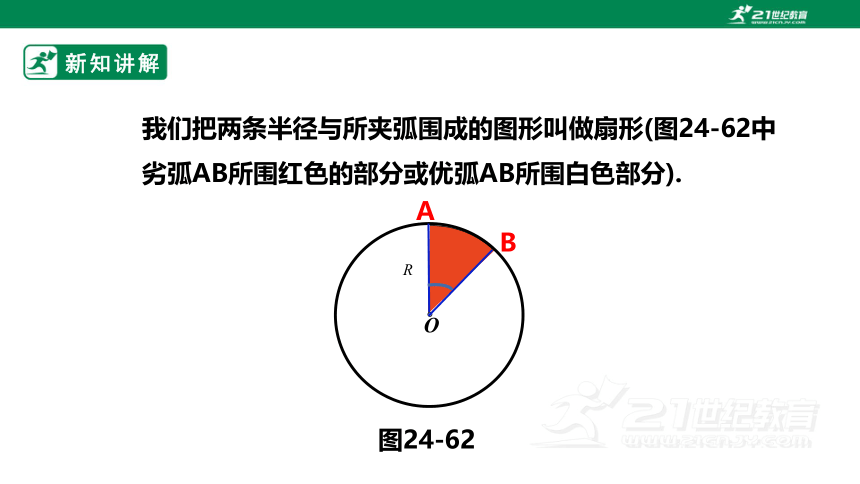
我们把两条半径与所夹弧围成的图形叫做扇形(图24-62中劣弧AB所围红色的部分或优弧AB所围白色部分).
O
R
图24-62
B
A
新知讲解
下列哪些图形是扇形?
√
×
×
×
扇形必须满足:两条半径所夹弧围成的图形
新知讲解
探究:如何求扇形的弧长和面积?
思考
新知讲解
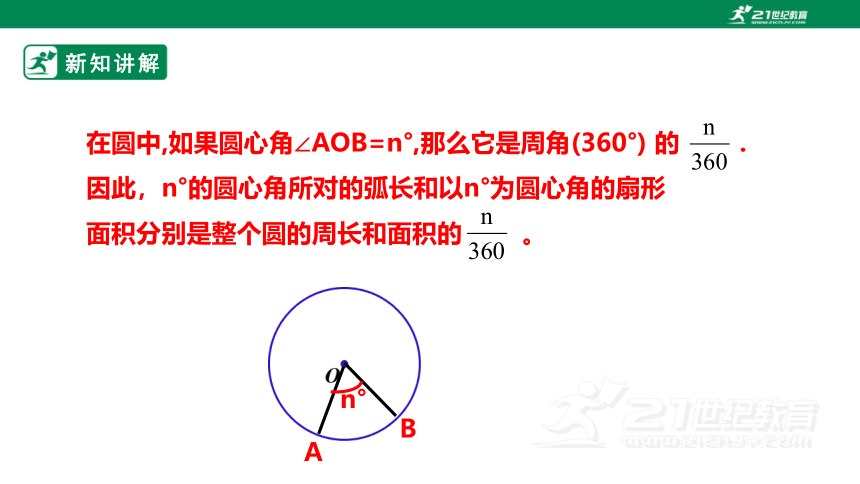
在圆中,如果圆心角∠AOB=n°,那么它是周角(360°) 的 .
因此,n°的圆心角所对的弧长和以n°为圆心角的扇形
面积分别是整个圆的周长和面积的 。
n°
B
A
新知讲解
(1)1 的圆心角所对的弧长 C1 是:
(2)30 的圆心角所对的弧长C1是:
n°
弧长C1计算方法:
新知讲解
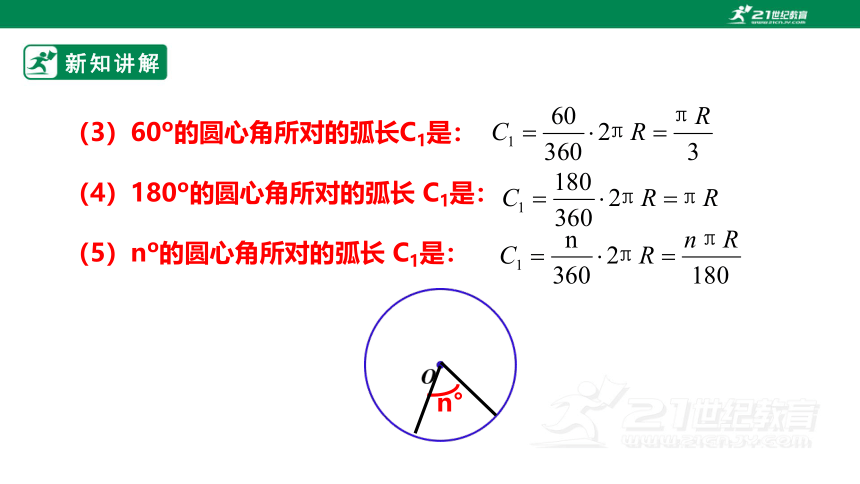
(3)60 的圆心角所对的弧长C1是:
(4)180 的圆心角所对的弧长 C1是:
(5)n 的圆心角所对的弧长 C1是:
n°
扇形面积S1的计算方法:
新知讲解
(1)1 的圆心角的扇形面积S1 是:
(2)30 的圆心角的扇形面积S1是:
n°
新知讲解
(3)60 的圆心角的扇形面积S1 是:
(4)180 的圆心角的扇形面积S1是:
(5)n 的圆心角的扇形面积S1是:
n°
新知讲解
总结:
n°的圆心角所对的弧长C1
n°为圆心角的扇形面积S1
注意: 用公式进行计算时,要注意公式中n的意义。
n表示1°圆心角的倍数,它是不带单位的。
新知讲解
弧长与扇形的面积与哪些因素有关呢
新知讲解
1、当圆心角大小不变时,对应的弧长(或扇形面积)与半径有关,半径越长,弧长(或面积)越大。
n°
O
R3>R2>R1
C3>C2>C1
S3>S2>S1
R3
R2
R1
新知讲解
2、当半径大小不变时,对应的弧长(或扇形面积)与圆心角有关,圆心角越大,弧长(或面积)越大。
n1°
O
n2°
n3°
n3°>n2°>n1°
C3>C2>C1
S3>S2>S1
新知讲解
例1 一滑轮装置如图 ,滑轮的半径R=10cm,当重物上升15.7 cm时,问滑轮的一条半径OA绕轴心О按逆时针方向旋转的角度 (假设绳索与滑轮之间没有滑动,π取3.14)
·
O
A
重物上升的高度等于半径OA绕轴心O旋转时点A所画的弧长。
新知讲解
解:设半径绕轴心O按逆时针方向旋转n°,则
解方程,得n≈90.
答:滑轮按逆时针方向旋转的角度约为90°.
·
O
A
例2 古希腊埃拉托塞尼曾给出一个估算地球周长(或子午圈长)的简单方法. 如图,点S和点A分别表示埃及的赛伊尼和亚历山大两地,亚历山大在赛伊尼的北方,两地的经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5 m). 当太阳光线在赛伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为α.实际测得α是7.2°,由此估算出了地球的周长,你能进行计算吗?
新知讲解
新知讲解
解 因为太阳光线可看作平行的,所以圆心角∠AOS=α=7.2°.
设地球的周长(即⊙O的周长)为C,则
=250000(希腊里)
≈39 625(km).
答:地球的周长约为39625km.
∴
O
α
A
S
1.如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A'OB',则A点运动的路径 的长为 ( )
A. π B. 2π C. 4π D. 8π
课堂练习
AA'
B
解:∵每个小正方形的边长都为1,
∴OA=4,
∵将△AOB绕点O顺时针旋转90°得到△A'OB',
∴∠AOA'=90° ,
∴A点运动的路径 的长为:
课堂练习
AA'
课堂练习
2.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则 的长为( )
A. 2π B. 4π C. 3π D.
CD
D
课堂练习
解:∵∠AOC:∠AOD:∠DOB=2:7:11,
∠AOD+∠DOB=180°,
∴∠AOD= ,∠DOB=110°,∠COA=20°.
∵OD=OC,CD=4,
∴2OD2=42.
∴OD= .
∴ 的长是
CD
课堂练习
3.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是 ( )
A. B. C. D. π-1
A
课堂练习
解:如图,连接BD,
设AD,BE相交于点G,BF,DC相交于点H,
∵四边形ABCD是菱形,∠A=60°,
∴△DAB是等边三角形,∠ADC=120°,
∴∠1=∠2=60°,
∵AB=2,
∴△ABD的高为 ,
课堂练习
∵扇形EBF的半径为2,圆心角为60°,
∴∠4+∠5=60°,
又∠3+∠5=60°,
∴∠3=∠4,在△ABG和△DBH中,
∵∠A=∠2 ,AB=DB,∠3=∠4),
∴△ABG≌△DBH(ASA),
∴S四边形GBHD=S△ABD,
∴S阴影=S扇形EBF-S△ABD=
故选A.
课堂总结
n°的圆心角所对的弧长C1
n°为圆心角的扇形面积S1
板书设计
24.7.1 弧长与扇形面积
1.弧长公式
2.扇形面积公式
作业布置
必做题:课本P57的第3~4题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.7.1 弧长与扇形面积
沪科版 九年级下
教学内容分析
本节在学习了圆的概念后,根据弧长占圆的周长的比例,推导圆的弧长公式,同时根据扇形占圆的比例,推导出扇形面积的公式,根据扇形、三角形、四边形面积公式求出组合图形的阴影面积。
教学目标
1.掌握弧长占圆的周长的比例,推导圆的弧长公式(重点)
2.推导和掌握扇形面积公式,并进行相关的计算(重点)
3.会利用扇形面积求三角形、四边形、圆、扇形等组合图形的面积(难点)
核心素养分析
掌握弧长占圆的周长的比例,推导圆的弧长公式,并推导圆的扇形面积公式,考查了学生的推理能力,学生掌握弧长与扇形面积的公式,并进行计算,培养了学生的计算能力,中考重点考查了求阴影部分的面积,其中含有扇形面积的计算。
新知导入
如何计算下图的弯道长度?
新知讲解
圆的面积公式?圆的周长公式是什么?
周长公式C=2πR
面积公式S=πR2
R
π=3.14159......是无理数,叫做圆周率
新知讲解
我们把两条半径与所夹弧围成的图形叫做扇形(图24-62中劣弧AB所围红色的部分或优弧AB所围白色部分).
O
R
图24-62
B
A
新知讲解
下列哪些图形是扇形?
√
×
×
×
扇形必须满足:两条半径所夹弧围成的图形
新知讲解
探究:如何求扇形的弧长和面积?
思考
新知讲解
在圆中,如果圆心角∠AOB=n°,那么它是周角(360°) 的 .
因此,n°的圆心角所对的弧长和以n°为圆心角的扇形
面积分别是整个圆的周长和面积的 。
n°
B
A
新知讲解
(1)1 的圆心角所对的弧长 C1 是:
(2)30 的圆心角所对的弧长C1是:
n°
弧长C1计算方法:
新知讲解
(3)60 的圆心角所对的弧长C1是:
(4)180 的圆心角所对的弧长 C1是:
(5)n 的圆心角所对的弧长 C1是:
n°
扇形面积S1的计算方法:
新知讲解
(1)1 的圆心角的扇形面积S1 是:
(2)30 的圆心角的扇形面积S1是:
n°
新知讲解
(3)60 的圆心角的扇形面积S1 是:
(4)180 的圆心角的扇形面积S1是:
(5)n 的圆心角的扇形面积S1是:
n°
新知讲解
总结:
n°的圆心角所对的弧长C1
n°为圆心角的扇形面积S1
注意: 用公式进行计算时,要注意公式中n的意义。
n表示1°圆心角的倍数,它是不带单位的。
新知讲解
弧长与扇形的面积与哪些因素有关呢
新知讲解
1、当圆心角大小不变时,对应的弧长(或扇形面积)与半径有关,半径越长,弧长(或面积)越大。
n°
O
R3>R2>R1
C3>C2>C1
S3>S2>S1
R3
R2
R1
新知讲解
2、当半径大小不变时,对应的弧长(或扇形面积)与圆心角有关,圆心角越大,弧长(或面积)越大。
n1°
O
n2°
n3°
n3°>n2°>n1°
C3>C2>C1
S3>S2>S1
新知讲解
例1 一滑轮装置如图 ,滑轮的半径R=10cm,当重物上升15.7 cm时,问滑轮的一条半径OA绕轴心О按逆时针方向旋转的角度 (假设绳索与滑轮之间没有滑动,π取3.14)
·
O
A
重物上升的高度等于半径OA绕轴心O旋转时点A所画的弧长。
新知讲解
解:设半径绕轴心O按逆时针方向旋转n°,则
解方程,得n≈90.
答:滑轮按逆时针方向旋转的角度约为90°.
·
O
A
例2 古希腊埃拉托塞尼曾给出一个估算地球周长(或子午圈长)的简单方法. 如图,点S和点A分别表示埃及的赛伊尼和亚历山大两地,亚历山大在赛伊尼的北方,两地的经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5 m). 当太阳光线在赛伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为α.实际测得α是7.2°,由此估算出了地球的周长,你能进行计算吗?
新知讲解
新知讲解
解 因为太阳光线可看作平行的,所以圆心角∠AOS=α=7.2°.
设地球的周长(即⊙O的周长)为C,则
=250000(希腊里)
≈39 625(km).
答:地球的周长约为39625km.
∴
O
α
A
S
1.如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A'OB',则A点运动的路径 的长为 ( )
A. π B. 2π C. 4π D. 8π
课堂练习
AA'
B
解:∵每个小正方形的边长都为1,
∴OA=4,
∵将△AOB绕点O顺时针旋转90°得到△A'OB',
∴∠AOA'=90° ,
∴A点运动的路径 的长为:
课堂练习
AA'
课堂练习
2.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则 的长为( )
A. 2π B. 4π C. 3π D.
CD
D
课堂练习
解:∵∠AOC:∠AOD:∠DOB=2:7:11,
∠AOD+∠DOB=180°,
∴∠AOD= ,∠DOB=110°,∠COA=20°.
∵OD=OC,CD=4,
∴2OD2=42.
∴OD= .
∴ 的长是
CD
课堂练习
3.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是 ( )
A. B. C. D. π-1
A
课堂练习
解:如图,连接BD,
设AD,BE相交于点G,BF,DC相交于点H,
∵四边形ABCD是菱形,∠A=60°,
∴△DAB是等边三角形,∠ADC=120°,
∴∠1=∠2=60°,
∵AB=2,
∴△ABD的高为 ,
课堂练习
∵扇形EBF的半径为2,圆心角为60°,
∴∠4+∠5=60°,
又∠3+∠5=60°,
∴∠3=∠4,在△ABG和△DBH中,
∵∠A=∠2 ,AB=DB,∠3=∠4),
∴△ABG≌△DBH(ASA),
∴S四边形GBHD=S△ABD,
∴S阴影=S扇形EBF-S△ABD=
故选A.
课堂总结
n°的圆心角所对的弧长C1
n°为圆心角的扇形面积S1
板书设计
24.7.1 弧长与扇形面积
1.弧长公式
2.扇形面积公式
作业布置
必做题:课本P57的第3~4题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
