人教版七年级下册第九章《不等式与不等式组》单元测试卷(含答案)
文档属性
| 名称 | 人教版七年级下册第九章《不等式与不等式组》单元测试卷(含答案) | 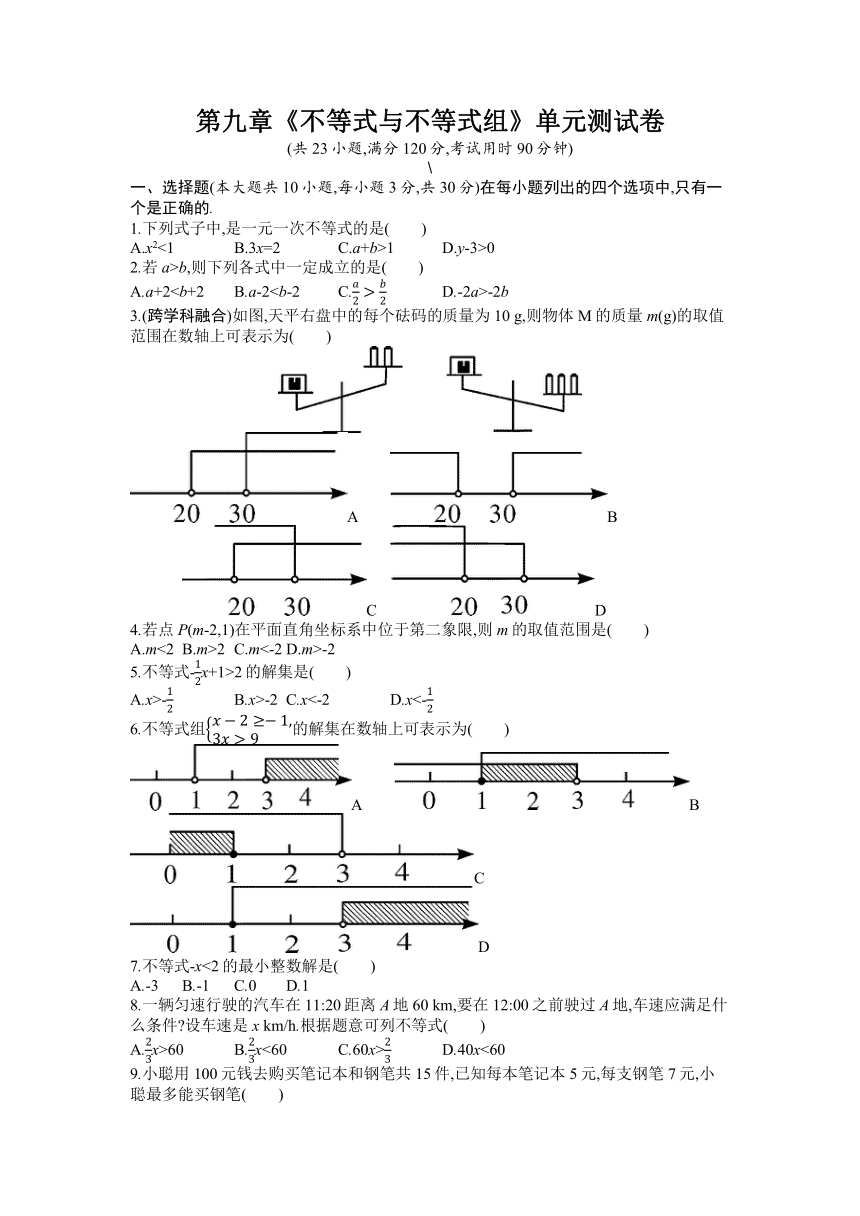 | |
| 格式 | docx | ||
| 文件大小 | 48.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 20:49:41 | ||
图片预览


文档简介
第九章《不等式与不等式组》单元测试卷
(共23小题,满分120分,考试用时90分钟)
\
一、选择题(本大题共10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的.
1.下列式子中,是一元一次不等式的是( )
A.x2<1 B.3x=2 C.a+b>1 D.y-3>0
2.若a>b,则下列各式中一定成立的是( )
A.a+2-2b
3.(跨学科融合)如图,天平右盘中的每个砝码的质量为10 g,则物体M的质量m(g)的取值范围在数轴上可表示为( )
A B C D
4.若点P(m-2,1)在平面直角坐标系中位于第二象限,则m的取值范围是( )
A.m<2 B.m>2 C.m<-2 D.m>-2
5.不等式-x+1>2的解集是( )
A.x>- B.x>-2 C.x<-2 D.x<-
6.不等式组的解集在数轴上可表示为( )
A B C D
7.不等式-x<2的最小整数解是( )
A.-3 B.-1 C.0 D.1
8.一辆匀速行驶的汽车在11:20距离A地60 km,要在12:00之前驶过A地,车速应满足什么条件 设车速是x km/h.根据题意可列不等式( )
A.x>60 B.x<60 C.60x> D.40x<60
9.小聪用100元钱去购买笔记本和钢笔共15件,已知每本笔记本5元,每支钢笔7元,小聪最多能买钢笔( )
A.10支 B.11支 C.12支 D.13支
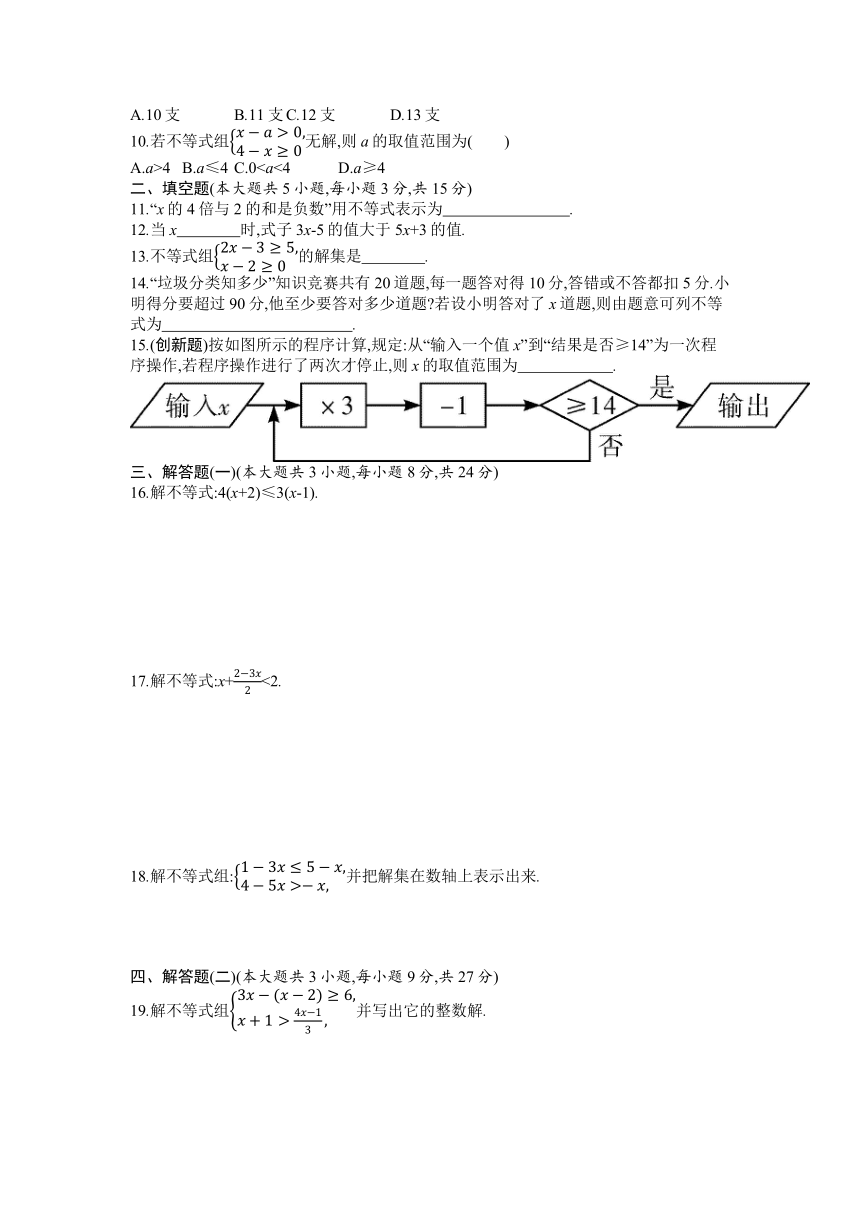
10.若不等式组无解,则a的取值范围为( )
A.a>4 B.a≤4 C.0二、填空题(本大题共5小题,每小题3分,共15分)
11.“x的4倍与2的和是负数”用不等式表示为 .
12.当x 时,式子3x-5的值大于5x+3的值.
13.不等式组的解集是 .
14.“垃圾分类知多少”知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分.小明得分要超过90分,他至少要答对多少道题 若设小明答对了x道题,则由题意可列不等式为 .
15.(创新题)按如图所示的程序计算,规定:从“输入一个值x”到“结果是否≥14”为一次程序操作,若程序操作进行了两次才停止,则x的取值范围为 .
三、解答题(一)(本大题共3小题,每小题8分,共24分)
16.解不等式:4(x+2)≤3(x-1).
17.解不等式:x+<2.
18.解不等式组:并把解集在数轴上表示出来.
四、解答题(二)(本大题共3小题,每小题9分,共27分)
19.解不等式组并写出它的整数解.
20.疫情过后,“地摊经济”火爆.张阿姨以每件80元的价格购进50件衬衫,在地摊上以每件100元的价格出售,她至少销售多少件衬衫,所得销售额才能超过进货总价
21.若使二元一次方程组中x的值为正数,y的值为负数,则m的取值范围是什么
五、解答题(三)(本大题共2小题,每小题12分,共24分)
22.为了对抗新冠病毒疫情,某医院现决定购买一批防护服,已知甲、乙两种型号的防护服的单价分别是310元,460元,且每种型号的防护服必须整套购买.
(1)若购买甲、乙两种型号防护服共100套,且恰好支出40 000元,甲、乙两种型号的防护服各购买了多少套
(2)若购买甲、乙两种型号的防护服共100套,且支出不超过36 000元,甲种型号的防护服至少要购买多少套
23.为了加强对校内外的安全监控,创建平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格、有效监控半径如下表所示.经调查,购买1台甲型设备比购买1台乙型设备少150元,购买3台甲型设备比购买2台乙型设备多150元.
甲型 乙型
价格(单位:元/台) a b
有效半径(单位:米/台) 100 150
(1)求a,b的值;
(2)若购买该批设备的资金不超过7 200元,则至少购买甲型设备多少台
(3)在(2)的条件下,若要求监控半径覆盖范围不低于1 600米,为了节约资金,请你设计一种最省钱的购买方案.
第九章《不等式与不等式组》单元测试卷
1.D 2.C 3.C 4.A 5.C 6.D 7.B 8.A 9.C 10.D
11.4x+2<0
12.<-4
13.x≥4
14.10x-5(20-x)>90
15.2≤x<5
16.解:4x+8≤3x-3,
4x-3x≤-3-8,
x≤-11.
17.解:x+<2,
2x+2-3x<4,
-x<2,x>-2.
18.解:
解不等式①得x≥-2,解不等式②得x<1,
∴不等式组的解集为-2≤x<1.
解集在数轴上表示如图:
19.解:解不等式3x-(x-2)≥6,得x≥2,
解不等式x+1>,得x<4,
则不等式组的解集为2≤x<4,
∴不等式组的整数解为2,3.
20.解:设销售x件衬衫,依题意有
100x>80×50,解得x>40,
∵x为整数,∴x最小是41.
答:她至少销售41件衬衫.
21.解:解
∵x的值为正数,y的值为负数,
∴解得22.解:(1)设购买甲种型号的防护服x套,购买乙种型号的防护服y套,由题意得
解得
答:购买甲种型号的防护服40套,购买乙种型号的防护服60套.
(2)设购买甲种型号的防护服m套,则购买乙种型号的防护服(100-m)套,由题意得
310m+460(100-m)≤36 000,解得m≥66,
∵m为整数,∴m的最小值为67.
答:甲种型号的防护服至少要购买67套.
23.解:(1)根据题意,得,解得.
(2)设购买甲型设备x台,则购买乙型设备(15-x)台.
根据题意,得450x+600(15-x)≤7 200,解得x≥12.
答:至少购买甲型设备12台.
(3)根据题意,得100x+150(15-x)≥1 600,
解得x≤13,∴12≤x≤13.∴x的取值为12或13.
共有两种购买方案:
方案一:购买甲型设备12台,乙型设备3台;
所需资金为450×12+600×3=7 200(元);
方案二:购买甲型设备13台,乙型设备2台;
所需资金为450×13+600×2=7 050(元).
∵7 200>7 050,∴方案二省钱.
答:最省钱的购买方案为购买甲型设备13台,乙型设备2台.
(共23小题,满分120分,考试用时90分钟)
\
一、选择题(本大题共10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的.
1.下列式子中,是一元一次不等式的是( )
A.x2<1 B.3x=2 C.a+b>1 D.y-3>0
2.若a>b,则下列各式中一定成立的是( )
A.a+2
3.(跨学科融合)如图,天平右盘中的每个砝码的质量为10 g,则物体M的质量m(g)的取值范围在数轴上可表示为( )
A B C D
4.若点P(m-2,1)在平面直角坐标系中位于第二象限,则m的取值范围是( )
A.m<2 B.m>2 C.m<-2 D.m>-2
5.不等式-x+1>2的解集是( )
A.x>- B.x>-2 C.x<-2 D.x<-
6.不等式组的解集在数轴上可表示为( )
A B C D
7.不等式-x<2的最小整数解是( )
A.-3 B.-1 C.0 D.1
8.一辆匀速行驶的汽车在11:20距离A地60 km,要在12:00之前驶过A地,车速应满足什么条件 设车速是x km/h.根据题意可列不等式( )
A.x>60 B.x<60 C.60x> D.40x<60
9.小聪用100元钱去购买笔记本和钢笔共15件,已知每本笔记本5元,每支钢笔7元,小聪最多能买钢笔( )
A.10支 B.11支 C.12支 D.13支
10.若不等式组无解,则a的取值范围为( )
A.a>4 B.a≤4 C.0
11.“x的4倍与2的和是负数”用不等式表示为 .
12.当x 时,式子3x-5的值大于5x+3的值.
13.不等式组的解集是 .
14.“垃圾分类知多少”知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分.小明得分要超过90分,他至少要答对多少道题 若设小明答对了x道题,则由题意可列不等式为 .
15.(创新题)按如图所示的程序计算,规定:从“输入一个值x”到“结果是否≥14”为一次程序操作,若程序操作进行了两次才停止,则x的取值范围为 .
三、解答题(一)(本大题共3小题,每小题8分,共24分)
16.解不等式:4(x+2)≤3(x-1).
17.解不等式:x+<2.
18.解不等式组:并把解集在数轴上表示出来.
四、解答题(二)(本大题共3小题,每小题9分,共27分)
19.解不等式组并写出它的整数解.
20.疫情过后,“地摊经济”火爆.张阿姨以每件80元的价格购进50件衬衫,在地摊上以每件100元的价格出售,她至少销售多少件衬衫,所得销售额才能超过进货总价
21.若使二元一次方程组中x的值为正数,y的值为负数,则m的取值范围是什么
五、解答题(三)(本大题共2小题,每小题12分,共24分)
22.为了对抗新冠病毒疫情,某医院现决定购买一批防护服,已知甲、乙两种型号的防护服的单价分别是310元,460元,且每种型号的防护服必须整套购买.
(1)若购买甲、乙两种型号防护服共100套,且恰好支出40 000元,甲、乙两种型号的防护服各购买了多少套
(2)若购买甲、乙两种型号的防护服共100套,且支出不超过36 000元,甲种型号的防护服至少要购买多少套
23.为了加强对校内外的安全监控,创建平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格、有效监控半径如下表所示.经调查,购买1台甲型设备比购买1台乙型设备少150元,购买3台甲型设备比购买2台乙型设备多150元.
甲型 乙型
价格(单位:元/台) a b
有效半径(单位:米/台) 100 150
(1)求a,b的值;
(2)若购买该批设备的资金不超过7 200元,则至少购买甲型设备多少台
(3)在(2)的条件下,若要求监控半径覆盖范围不低于1 600米,为了节约资金,请你设计一种最省钱的购买方案.
第九章《不等式与不等式组》单元测试卷
1.D 2.C 3.C 4.A 5.C 6.D 7.B 8.A 9.C 10.D
11.4x+2<0
12.<-4
13.x≥4
14.10x-5(20-x)>90
15.2≤x<5
16.解:4x+8≤3x-3,
4x-3x≤-3-8,
x≤-11.
17.解:x+<2,
2x+2-3x<4,
-x<2,x>-2.
18.解:
解不等式①得x≥-2,解不等式②得x<1,
∴不等式组的解集为-2≤x<1.
解集在数轴上表示如图:
19.解:解不等式3x-(x-2)≥6,得x≥2,
解不等式x+1>,得x<4,
则不等式组的解集为2≤x<4,
∴不等式组的整数解为2,3.
20.解:设销售x件衬衫,依题意有
100x>80×50,解得x>40,
∵x为整数,∴x最小是41.
答:她至少销售41件衬衫.
21.解:解
∵x的值为正数,y的值为负数,
∴解得
解得
答:购买甲种型号的防护服40套,购买乙种型号的防护服60套.
(2)设购买甲种型号的防护服m套,则购买乙种型号的防护服(100-m)套,由题意得
310m+460(100-m)≤36 000,解得m≥66,
∵m为整数,∴m的最小值为67.
答:甲种型号的防护服至少要购买67套.
23.解:(1)根据题意,得,解得.
(2)设购买甲型设备x台,则购买乙型设备(15-x)台.
根据题意,得450x+600(15-x)≤7 200,解得x≥12.
答:至少购买甲型设备12台.
(3)根据题意,得100x+150(15-x)≥1 600,
解得x≤13,∴12≤x≤13.∴x的取值为12或13.
共有两种购买方案:
方案一:购买甲型设备12台,乙型设备3台;
所需资金为450×12+600×3=7 200(元);
方案二:购买甲型设备13台,乙型设备2台;
所需资金为450×13+600×2=7 050(元).
∵7 200>7 050,∴方案二省钱.
答:最省钱的购买方案为购买甲型设备13台,乙型设备2台.
