苏教版六年级下册数学 作业课件 第四单元 比 例 44张幻灯片(共44张PPT)
文档属性
| 名称 | 苏教版六年级下册数学 作业课件 第四单元 比 例 44张幻灯片(共44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 15:09:13 | ||
图片预览










文档简介
(共44张PPT)
第四单元
四 比 例
第1课时 图形的放大和缩小
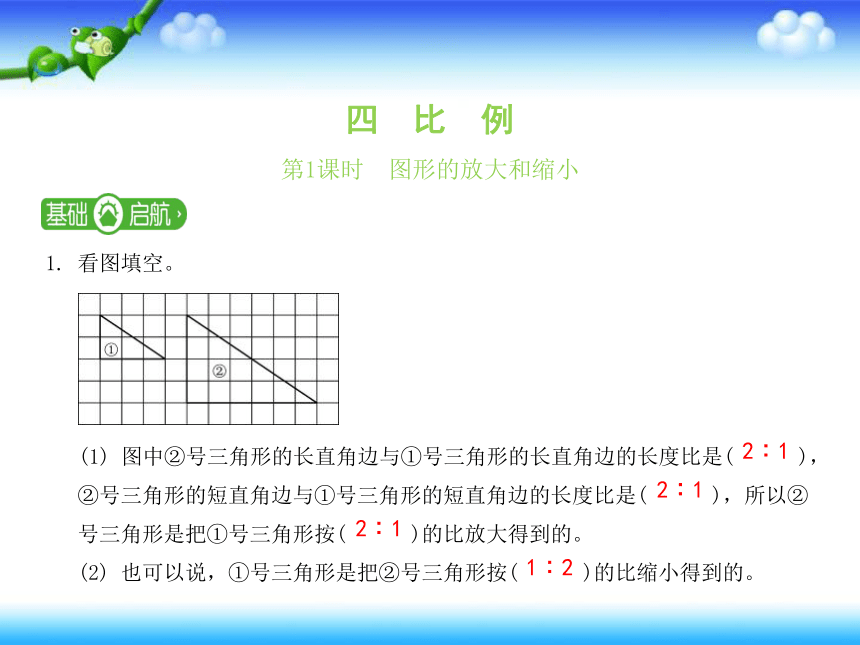
1. 看图填空。
(1) 图中②号三角形的长直角边与①号三角形的长直角边的长度比是( ),
②号三角形的短直角边与①号三角形的短直角边的长度比是( ),所以②
号三角形是把①号三角形按( )的比放大得到的。
(2) 也可以说,①号三角形是把②号三角形按( )的比缩小得到的。
2∶1
2∶1
2∶1
1∶2
2. 填空。
(1) 一个圆形零件,直径是4毫米,将其按( )∶( )的比( )(填“放
大”或“缩小”)后,直径是2厘米。
(2) 把一个图形的每条边放大为原来的4倍,就是把这个图形按( )的比放
大。
(3) 一幅字画的长是16分米,宽是5分米,把它按( )的比缩小,长是32厘
米,宽是( )厘米。
(4) 电脑上有一张长24厘米、宽 8厘米的长方形图片,拖动电脑鼠标后,图片的
长是6厘米,宽是2厘米,相当于把这张图片按( )的比缩小了。
5
1
放大
4∶1
1∶5
10
1∶4
3. 选择。
(1) 无论什么样的图形,按一定的比放大或缩小后,与原来的图形相比,大小
( ),形状( )。
① 不变 ② 变了 ③ 无法确定
(2) 把一个长方形按1∶2的比缩小后,各条边的长都是原来的( )。
① 2倍 ② ③ 4倍 ④
(3) 下面描述的现象中,属于把图形放大的是( ),属于把图形缩小的是( )。
① 小明去照相馆拍了一张自己的2寸照片
② 李大爷用放大镜仔细地看报纸
③ 小红照哈哈镜
②
①
②
②
①
4. 按2∶1的比画出平行四边形放大后的图形;
按1∶2的比画出下面图形缩小后的图形。
5. 一个直角三角形的三条边的长度分别是6厘米、8厘米、10厘米,按一定的比放
大后,最长边长50厘米,另两条边分别长多少厘米?
50÷10=5 5×6=30(厘米) 5×8=40(厘米)
解析:先求出最长边之间的倍数关系,再求另两条边的长度。
第2课时 比例的意义
1. 填空。
(1) 表示( )叫作比例。
(2) 5∶2的比值是( ),∶的比值是( ),因为比值( ),所以这两
个比可以组成比例( )。
(3) 写出比值是的两个比,并将它们组成比例:(
)。
(4) 用20以内的四个合数组成一个比例是( )。
两个比相等的式子
相等
5∶2=∶
答案不唯一,如4∶5=
答案不唯一,如4∶6=12∶18
8∶10
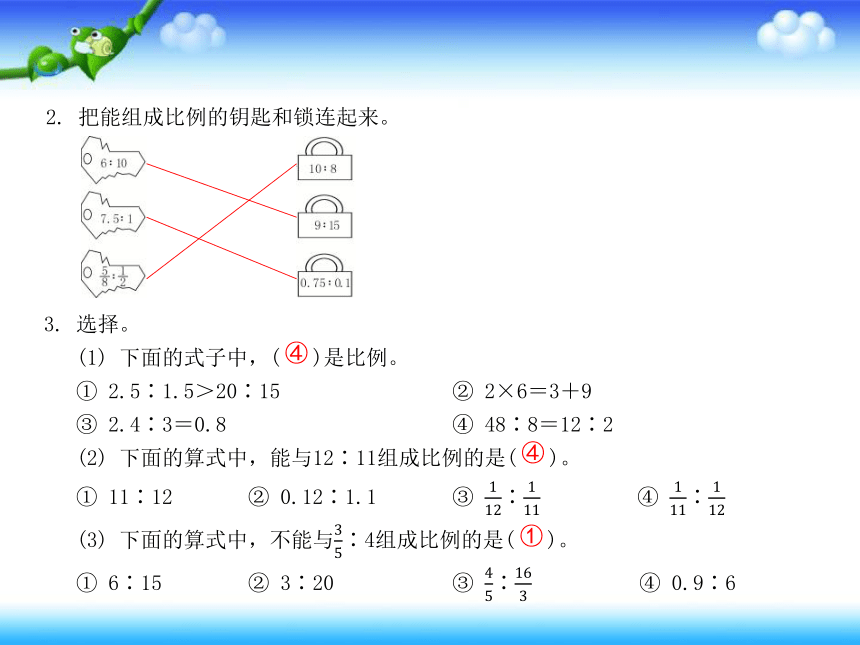
2. 把能组成比例的钥匙和锁连起来。
3. 选择。
(1) 下面的式子中,( )是比例。
① 2.5∶1.5>20∶15 ② 2×6=3+9
③ 2.4∶3=0.8 ④ 48∶8=12∶2
(2) 下面的算式中,能与12∶11组成比例的是( )。
① 11∶12 ② 0.12∶1.1 ③ ∶ ④ ∶
(3) 下面的算式中,不能与∶4组成比例的是( )。
① 6∶15 ② 3∶20 ③ ∶ ④ 0.9∶6
④
④
①
4. 李师傅上午3小时加工零件240个,下午5小时加工零件400个。
(1) 比一比李师傅上午加工零件的个数和时间的比及下午加工零件的个数和时间
的比,这两个比能组成比例吗?如果能,写出来。
(2) 比一比李师傅上、下午加工零件个数的比和上、下午加工时间的比,这两个
比能组成比例吗?如果能,写出来。
5. 将下图中的长方形按3∶1的比放大,然后观察图中数据,你能根据图中数据写出
哪些比例?(写出2个即可)
图略 答案不唯一,如9∶3=6∶2 9∶6=3∶2
240∶3=80 400∶5=80 能 240∶3=400∶5
240∶400=0.6 3∶5=0.6 能 240∶400=3∶5
6. 如图,在线段AG中,AB=BC=CD=DE=EF=FG,你能根据它们间的长度,将下列
比例补充完整吗?
(1) AB∶BC=( )∶( )
(2) ( )∶( )=BG∶DG
(3) BC∶AE=( )∶( )
(4) ( )∶( )=BF∶AG
CD
DE
(答案不唯一)
AF
AD
CD
CG
AE
AG
7. 观察图①,照样子把图②按4∶1的比放大。
解析:按4∶1的比放大就是对应线段的长度是原长度的4倍。
第3课时 比例的基本性质
1. 填空。
(1) 如果1.4∶a=b∶7(a、b不为0),那么1.4×( )=( )×( )。
(2) 如果3a=5b(a、b不为0),那么a∶b=( )∶( )。
(3) =
(4) 在一个比例中,两个外项互为倒数,其中一个内项是10以内最大的合数,另
一个内项是( )。
(5) 如果甲的与乙的相等(甲、乙不为0),那么乙∶甲=( )∶( )。
(6) 在一个比例中,两个比的比值都是1.5,这个比例的两个外项分别是12和45,
这个比例是( )或( )。
(7) 在比例12∶45=8∶30中,如果第一个比的后项增加15,那么第二个比的前
项应该( )才能使比例成立。
7
a
b
5
3
(答案不唯一)
24
3
25
28
12∶8=67.5∶45
45∶30=18∶12
减少2
2. 判断。
(1) 用比例中两个外项的积减去两个内项的积,结果是0。 ( )
(2) 5∶4和∶可以组成比例。 ( )
(3) 在比例中交换两个外项的位置,比例依然成立。 ( )
(4) 因为4×6=3×8,所以4∶6=3∶8。 ( )
(5) 在比例中,两个外项不变,一个内项缩小为原来的,另一个内项扩大为原
来的3倍,比例依然成立。 ( )
3. 根据比例的基本性质判断哪组中的两个比可以组成比例,并把能组成的比例写
出来。
(1) ∶和∶ (2) ∶0.3和3.2∶
(1) ×= ×= ≠ 不能
(2) 0.3×3.2=0.96 ×=0.96 0.96=0.96 能 ∶0.3=3.2∶
√
√
×
√
√
4. 选择。
(1) 能与∶组成比例的是( )。
① ∶5 ② ∶ ③ 5∶4 ④ ∶
(2) 因为10∶5=3.6∶1.8,所以( )。
① 10×3.6=5×1.8 ② 5×10=1.8×3.6
③ 10×1.8=5×3.6 ④ 3.6÷5=10÷1.8
(3) 用、、30、24四个数组成的比例是( )。
① ∶=30∶24 ② ∶=30∶24
③ ∶24=∶30 ④ 30∶ =∶24
③
③
②
5. 把下面两组数组成的比例写出来。(写一个即可)
(1) 0.7、7、8和80
(2) 、、和
6. 在比例a∶b=c∶d中,a+d=38,d-a=22,a∶b与c∶d的比值均为,这个比
例是多少?
答案不唯一,如0.7∶7=8∶80
答案不唯一,如∶=∶
(38-22)÷2=8 8+22=30 8÷=5 30×=48 8∶5=48∶30
7. 已知a∶10=4∶b,那么ab+4的值是多少?
10×4=40 40+4=44 解析:根据比例的基本性质先求ab的值,再加4求出问题的答案。
第4课时 解比例
1. 填空。
(1) 妈妈手表上的一个零件长5毫米,把它按9∶1的比画在图上,零件在图上应
画( )厘米。
(2) 上海东方明珠塔高468米,江工程师按1∶200的比制作了一个模型,模型高
( )米。
2. 根据比例的基本性质,在括号里填合适的数。
15∶6=( )∶2 =
2.5∶5=( )∶20 ( )∶3.5=0.6∶7
4.5
2.34
5
10
0.3
( )
32
40
3. 解比例。
2.4∶0.25=6.4∶x x∶1.2=25∶7.5
= x∶0.3=
4. 根据条件写出比例,再解比例。
(1) x和8的比等于4和的比。
(2) 一个比例两个外项是1.25和1.6,两个内项是2.5和x。
x=
x=4
x=16
x=
x∶8=4∶ x=160
1.25×1.6=2.5x x=0.8
5. 把左边的平行四边形按比例缩小后得到右边的平行四边形,求未知数x。
6. 一个等腰三角形花圃的底和高的长度比是3∶2,底是24米,高是多少米?面积是
多少平方米?
7. 妈妈调制一杯蜂蜜水,400克水中放了20克蜂蜜。涛涛和妹妹想配制同样口味的
蜂蜜水,如果有600克水,需要放多少克蜂蜜?
6∶x=12∶8 x=4
设高是x米。 24∶x=3∶2 x=16
24×16÷2=192(平方米)
设需要放x克蜂蜜。 400∶20=600∶x x=30
8. 小刚家今年收向日葵吨,如果千克向日葵可榨油千克,这批向日葵共可榨油
多少千克?
设这批向日葵共可榨油x吨。∶=∶x x=0.14 0.14吨=140千克
9. 一个数,它能和、2、6组成比例,这个数可能是( ),组成的比例是(
);还可能是( ),组成的比例是( );还可能是( ),
组成的比例是( )。
∶6=
∶2
1
∶2=1∶6
36
2∶=36∶6
(比例答案不唯一)
解析:可以设这个数为x,根据比例的性质,列出方程,解出x。
第5课时 比例尺的意义
1. 填空。
(1) 比例尺表示( )和( )的比。
(2) 在比例尺是1∶8000000的地图上,图上距离是实际距离的 ,图
上1厘米表示实际距离( )千米。
(3) 杭州湾大桥全长大约是36千米。在一幅地图上量得杭州湾大桥的长是7.2厘
米,这幅地图的比例尺是( )。
(4) 在一张精密零件的图纸上,1厘米表示实际长度2毫米。这张图纸的比例尺是
( )。
(5) 把线段比例尺 改写成数值比例尺是( )。
(6) 一幅图的比例尺是1∶3000,如果改写成线段比例尺是( )。
图上距离
实际距离
( )
( )
1
8000000
80
1∶500000
5∶1
1∶6000
2. 判断。
(1) 比例尺是一个前项为1的比。 ( )
(2) 比例尺100∶1表示图上距离是实际距离的100倍。 ( )
(3) 有一幅图,图上2厘米表示实际距离150米,这幅图的比例尺是。 ( )
(4) 把线段比例尺 改写成数值比例尺是1∶9000000。 ( )
3. 选择。
(1) 一幅图上,图上距离6厘米表示实际距离24米,这幅图的比例尺是( )。
① 1∶4 ② 1∶400 ③ 400∶1
(2) 小东有一张长5厘米、宽3厘米的卡片。选比例尺( )画图最大,选比例尺
( )画图最小。
① 2∶1 ② 1∶2 ③ 1∶4
(3) 一幅图上,图上距离7分米表示实际距离7毫米,这幅图的比例尺是( )。
① 1∶1 ② 1∶100 ③ 100∶1
√
×
×
×
②
①
③
③
4. 从北京到杭州的实际距离大约是1200千米,在一幅地图上量得两地之间的距离是
6厘米,求这幅地图的比例尺。
5. 学校的操场长120米,宽 80米,下面是这个操场的平面图。量一量,求出这个平
面图的比例尺,并用线段比例尺表示出来。
6. 一只蚂蚁的实际长度是5mm,画在一幅图上的长是3cm,这幅图的比例尺是多少?
3 cm=30 mm
30∶5=6∶1
1200千米=120000000厘米 6∶120000000=1∶20000000
120米=12000厘米
3∶12000=1∶4000 图略
7. 一块长方形地的实际长是200米,宽是80米,小明在一幅平面图上画出的这块地
的长是10厘米,宽是8厘米,小明画得对吗?
200∶80=5∶2 10∶8=5∶4 5∶2≠5∶4 小明画得不对
解析:按比例放大和缩小只改变图形的大小,不改变形状,先分别求出两个长方形长与宽的比,再看比是否相同。
第6课时 比例尺的实际应用
1. 填表。
图上距离 实际距离 比例尺
20厘米 4千米
15厘米 1∶500000
12千米 1∶200000
30厘米 300∶1
1∶20000
75千米
1毫米
6厘米
2. 下面是光明小学校园的平面图。
(1) 图上1厘米的线段表示实际距离( )厘米。
(2) 量一量平面图中教学楼的长是( )厘米,宽是( )厘米。教学楼实际的
长是( )米,宽是( )米,占地面积是( )平方米。
3. 从一幅地图上量得宁通高速公路长4厘米,已知这幅地图的比例尺是1∶4000000。
宁通高速公路实际长多少千米?
4. 北京故宫是中国现存规模最大、保存最完整的古建筑群,占地呈长方形,南北
长约960米,东西宽约750米,把它画在比例尺是 1∶6000的图上,长和宽分别
是多少厘米?
1200
3
1
36
12
432
4×4000000=16000000(厘米)=160千米
960米=96000厘米 750米=75000厘米
长:96000÷6000=16(厘米) 宽:75000÷6000=12.5(厘米)
5.
(1) 鹏鹏家到学校的距离是1200米,图上距离是( )厘米,这幅图的比例尺是
( )。
(2) 在(1)的条件下,从学校到图书馆的图上距离是( )厘米,实际距离是
( )米。
6. 在比例尺为 的地图上,量得北京到南京的铁路长度是 14厘米,
一列高铁以每小时350千米的速度从南京开往北京,需要多少小时?
1
1∶120000
2
2400
75×14÷350=3(小时)
7. 在一幅比例尺为1∶20000的地图上,量得学校到游乐场的距离是15厘米,在另
一幅比例尺是的地图上,学校到游乐场的距离是多少厘米?
15×20000×=5(厘米)
8. 在比例尺是1∶20000000的地图上,A、B 两地相距4.5厘米,甲、乙两车同时从
A、B两地出发,以7∶8的速度相对开出,相遇时甲车比乙车少行多少千米?
20000000厘米=200千米 4.5×200÷(8+7)=60(千米)
解析:时间相同,速度比等于路程比,所以甲车与乙车行驶的路程比是7∶8,全程共15份,甲车正好比乙车少行1份,求出1份是多长就行。
第7课时 练 习 课
1. 填空。
(1) 4、5、10和另一个数可以组成一个比例,这个数可能是( )、( )或( )。
(2) 在一幅图上,量得A、B两个景点的图上距离是3厘米,A、B两个景点的实际
距离是900米,这幅图的比例尺是( )。
(3) 南京到上海的实际距离大约是300千米,画在一幅比例尺是1∶5000000的地
图上,应画( )厘米。
(4) 某个零件长2毫米,如果画在比例尺是25∶1的图纸上,应画( )厘米。
(5) 在比例尺是 的地图上,某段国道长20厘米,这段国道实际长
( )千米。如果在另一幅地图上,这段国道的长度扩大了2倍,另一幅图的
比例尺是( )。
2
8
12.5
1∶30000
6
5
800
1∶2000000
2. 判断。
(1) 由两个比组成的式子叫作比例。 ( )
(2) 为便于计算,比例尺前项或后项一般为1。 ( )
(3) 在比例中,两个外项的积与两个内项的积的比是1∶1。 ( )
(4) 在比例尺是20∶1的图上,实际距离是图上距离的20倍。 ( )
3. 解比例。
x∶= ∶3 0.06∶0.5=0.12∶x
√
√
×
×
x=
x=1
4. 下面是育才小学附近的平面图。
(1) 量出育才小学到新华书店的图上距离,再算出它们之间的实际距离。
(2) 超市在育才小学的正东方向3千米处,电影院在育才小学的正西方向2500米
处。算一算,并在图中标出超市和电影院的位置。
图上距离:1厘米 1×100000=100000(厘米)=1千米
3千米=300000厘米 300000÷100000=3(厘米)
2500米=250000厘米 250000÷100000=2.5(厘米) 图略
5. 下面是淘淘家与游乐园之间的路线图。
(1) 已知淘淘家与展览馆之间的实际距离是3千米。量一量,将图中比例尺补全。
(2) 妈妈准备带淘淘打的经过展览馆到游乐园。出租车3千米以内的收费为 9元,
以后每增加1千米的收费为2.4元。从家到游乐园打的需要多少元?
3÷1.5=2(千米) 图略
(1.5+4)×2=11(千米) (11-3)×2.4+9=28.2(元)
6. 如图,AD=8厘米,BE=12厘米,AC+BC=25厘米,三角形ABC的面积是多少?
BC×AD÷2=AC×BE÷2 BC×AD=AC×BE AC∶BC=AD∶BE
AC∶BC=8∶12=2∶3 25÷(2+3)×3=15(厘米)
15×8÷2=60 (平方厘米) 解析:可以根据三角形面积
的两种不同计算方法得到一个比例式,再求出AC与BC的比,接着根据AC与BC的和求出BC的长,最后求出三角形的面积。
第8课时 面积的变化
1. 填空。
(1) 如右图,量一量,算一算,大平行四边形与小平行四边形底
的比是( ),高的比是( ),面积的比是( )。
(2) 如果一个圆的半径扩大为原来的2倍,那么直径扩大为原来的( )倍,周
长扩大为原来的( )倍,面积扩大为原来的( )倍。
(3) 如果一幅建筑施工图的比例尺是 1∶1000,那么这幅建筑施工图的图上面
积与实际面积的比是( )。
(4) 如果把一个图形按1∶m的比缩小,缩小后与缩小前图形的面积比是( )。
2∶1
2∶1
4∶1
2
2
4
1∶1000000
1∶m2
2. 判断
(1) 将一个图形按一定的比放大或缩小后,图形中所有线段都按相同的比放大
或缩小了。 ( )
(2) 一个等边三角形放大后的面积是原来的25倍,高一定是原来的5倍。 ( )
(3) 在比例尺是1∶8的图纸上,甲、乙两个圆的半径比是2∶3,那么甲、乙两
个圆实际的半径比也是2∶3。 ( )
3. 选择。
(1) 把一张照片按5∶1的比放大,放大后和放大前照片的面积比是( )。
① 10∶1 ② 1∶25 ③ 25∶1
(2) 在比例尺是4∶1的图纸上,一朵胸花的实际面积是3平方厘米,图上面积是
( )平方厘米。
① 3 ② 12 ③ 48
(3) 如右图,将一个小正方体按 2∶1 的比放大,新的正方体与原
正方体表面积的比是( ),体积比是( )。
① 2∶1 ② 4∶1 ③ 8∶1
√
√
√
③
③
②
③
4. 有一块边长为60米的正方形草坪,在一幅比例尺是1∶2000的平面图上,这块草
坪的图上面积是多少?
5. 在一幅比例尺是 的校园平面图上,学校的操场如下图。(取整厘
米数)
(1) 量一量,算一算,求出操场的图上面积和实际面积。
(2) 写出图上面积与实际面积的比,并与比例尺进行比较,你发现了什么?
60米=6000厘米 6000÷2000=3(厘米) 3×3=9(平方厘米)
图上面积:2×3=6(平方厘米)
实际面积:(2×40)×(3×40)=9600(平方米)
9600平方米=96000000平方厘米 6∶96000000=1∶16000000
40米=4000厘米 12∶40002=1∶16000000
比例尺的平方等于图上面积与实际面积的比
6. 把一个面积是16平方厘米的正方形放大,放大后的正方形的面积是原来正方形面
积的9倍。放大后的正方形的边长是多少厘米?
16×9=144(平方厘米) 144=12×12 边长是12厘米
7. 将一个小圆放大成一个大圆,它们的面积之差是 209 cm2,小圆的周长是大圆周
长的。你能求出小圆的面积吗?
92∶102=81∶100 209÷(100-81)×81=891(cm2)
解析:面积比是长度比的平方,根据周长比为9∶10,先求出面积比为
81∶100,再利用面积差求出小圆面积。
满分:100分 时间:60分钟 得分:_____
第四单元自主检测
一、填空。(每空1分,共24分)
1. 从24的因数中选四个数,组成一个比例是( )。
2. 在2、3、4、5、6中去掉( ),剩下的四个数可组成比例。
3. 若∶x和12∶20能组成比例,则x等于( )。
4. 在5∶3=15∶9中,将3扩大为原来的5倍,9增加( ),比例仍然成立。
5. 将底是4厘米、高是3厘米的平行四边形按( )的比放大,可得到底是12厘米、
高是( )厘米的平行四边形,新的平行四边形和原图形的面积比是( )。
6. 将高100米、面积为5000平方米的梯形按1∶2000的比缩小,新梯形高( )厘米,
面积是( )平方厘米。
答案不唯一,如1∶2=12∶24
5
36
3∶1
9
9∶1
5
12.5
7. 一幅图的比例尺是 ,在这幅图上,图上距离是12厘米,实际距离
是( )千米,实际距离是225千米,图上距离是( )厘米。
8. 一幅图的图上距离4厘米表示实际距离2千米,这幅图的比例尺是( ),
一条16千米长的路画在这幅图上长( )。
9. 一种零件长5毫米,把它画在比例尺是10∶1的图上应画( )厘米,在这幅图上
量得另一种零件长7.2厘米,实际长( )毫米。
10. 在比例尺是的图上,量得一个正方形的面积是9平方厘米,它的实际面积是
( )平方米。
11. 完成下表:
540
5
1∶50000
32厘米
5
7.2
900
图上距离 实际距离 比例尺
2.4厘米 1∶4000
3厘米 420千米
4800千米 1∶50000000
9.6厘米
96米
1∶14000000
12. 用4、3、15和x可以组成比例,x最大是( ),x最小是( )。
13. 如右图,A、B两个图形重叠在一起,重叠部分的面积是A的,是B的
,A、B两个图形面积的比是( )。
14. 一个比例的两个内项是3和8,两个比的比值都是,这个比例是( )
或( )。
二、判断。(每题1分,共6分)
1. 一幅世界地图的比例尺是1∶50000。 ( )
2. 根据比例的基本性质可以解比例。 ( )
3. 将一个图形放大或缩小后,图形的大小改变,形状不变。 ( )
4. 如果一幅地图的比例尺是1∶500,那么图上面积与实际面积的比是1∶500。( )
5. 在同一幅图上,图上距离越长,实际距离也越长。 ( )
6. 如果5x=10y(x、y都不等于0),那么x∶y=2∶1。 ( )
20
2∶3
1∶3=8∶24
∶8=3∶9
√
√
×
√
√
×
三、选择。(每题1分,共6分)
1. 下面各比中,能与∶组成比例的是( )。
① 3∶4 ② 4∶3 ③ 4∶9 ④ 9∶4
2. 一幅地图的比例尺是 ,关于这个比例尺,下面表述正确的是( )。
① 图上距离是实际距离的
② 图上距离是实际距离的
③ 图上距离和实际距离的比是1∶900
④ 图上距离1千米表示实际距离30千米
3. 如果a<b<c<d(a≠0),且利用 a、b、c、d 四个数能组成比例,那么下面算式
( )可能是正确的。
① a∶b=d∶c ② b∶a=c∶d
③ a∶c=b∶d ④ c∶b=a∶d
③
②
③
4. 在两个圆中,它们的半径比与它们的( )不可以组成比例。
① 直径比 ② 周长比
③ 面积比 ④ 直径比或周长比
5. 一个电子零件的实际长度是2毫米,画在图纸上是4厘米,这张图纸的比例尺是
( )。
① 1∶20 ② 20∶1
③ 2∶1 ④ 1∶2
6. 红关小学新建一个长方形游泳池,长100米,宽50米。把它画在长15厘米、宽10
厘米的纸上,在下面各比例尺中,选用( )不合适。
① 1∶1000 ② 1∶500
③ 1∶2000 ④ 1∶5000
③
②
②
四、计算。(共18分)
1. 解比例。(12分)
x∶3=∶ = ∶x= ∶ 8∶x=
2. 将下图左边的三角形按比例缩小后得到右边的三角形,求未知数x。(3分)
3. 下图中小平行四边形放大后得到大平行四边形,求大平行四边形的高。(单位:
分米)(3分)
设大平行四边形的高为x分米。
12.8∶x=3.2∶1.2
x=4.8
3.2∶1.6=4.8∶x
x=2.4
x=
x=
x=
x=64
五、操作。(每题3分,共6分)
1. 按1∶3的比画出三角形缩小后的图形。
2. 按2∶1的比画出圆放大后的图形,并和原来的圆组成一个圆环。
六、解决问题。(共40分)
1. 有一幅中国地图。
(1) 这幅地图的比例尺是多少?(2分)
(2) 南京到上海的实际距离大约是320千米。在这幅地图上,南京到上海的距离
大约是多少厘米?(2分)
(3) 在这幅地图上,北京到广州的距离大约是48厘米,那么北京到广州的实际距
离大约是多少千米 (2分)
1∶5000000
5000000厘米=50千米 320÷50=6.4(厘米)
48×50=2400(千米)
2. 胡夫金字塔的高度是136.5米,如果按1∶10的比缩小,建造一座胡夫金字塔模型,
那么这座金字塔模型的高度是多少米?(5分)
3. 一张照片长4厘米,宽3厘米,如果按4∶1的比放大,放大后的长是多少厘米?如
果要使放大后的宽是15分米,就要按几比几放大?(5分)
4. 一种药水,药和水的比是3∶200。配置这种药水,270克药需加水多少千克?4吨
水需加药多少千克?(5分)
5. 甲、乙两地相距420千米,在一幅图上甲、乙两地的距离是6厘米,在这幅图上乙、
丙两地相距18厘米,乙、丙两地的实际距离是多少千米? (5分)
136.5÷10=13.65(米)
4×4=16(厘米) 15分米=150厘米 150∶3=50∶1
水:270÷3×200=18000(克)=18千克
药:4÷200×3=0.06(吨)=60千克
18÷6×420=1260(千米)
6. 在比例尺是1∶4000000的地图上量得A、B两地的距离是8厘米,一列汽车以每小
时100千米的速度从A地开往B地,几小时可以行完全程的?(4分)
7. 下图是某小学操场的平面图,这个操场长150米。求这幅平面图的比例尺,并在
括号里填合适的数,在方框里填合适的单位。这个操场的实际面积是多少平方
米?(5分)
8×4000000=32000000(厘米)=320千米 320×÷100=2.4(小时)
150÷5=30(米) 比例尺为1∶3000
3×30=90(米) 150×90=13500(平方米)
30
60
90
米
8. 新世纪农场有一个长方形果园,长 1500米,宽 1200米。先选择合适的比例尺,
在其后面的括号里画“√”,并计算出图上的长和宽,再画出这个果园的平面
图。(5分)
1∶3000( ) 1∶30000( ) 1∶300000( )
30000厘米=300米
长:1500÷300=5(厘米)
宽:1200÷300=4(厘米)
图略
√
第四单元
四 比 例
第1课时 图形的放大和缩小
1. 看图填空。
(1) 图中②号三角形的长直角边与①号三角形的长直角边的长度比是( ),
②号三角形的短直角边与①号三角形的短直角边的长度比是( ),所以②
号三角形是把①号三角形按( )的比放大得到的。
(2) 也可以说,①号三角形是把②号三角形按( )的比缩小得到的。
2∶1
2∶1
2∶1
1∶2
2. 填空。
(1) 一个圆形零件,直径是4毫米,将其按( )∶( )的比( )(填“放
大”或“缩小”)后,直径是2厘米。
(2) 把一个图形的每条边放大为原来的4倍,就是把这个图形按( )的比放
大。
(3) 一幅字画的长是16分米,宽是5分米,把它按( )的比缩小,长是32厘
米,宽是( )厘米。
(4) 电脑上有一张长24厘米、宽 8厘米的长方形图片,拖动电脑鼠标后,图片的
长是6厘米,宽是2厘米,相当于把这张图片按( )的比缩小了。
5
1
放大
4∶1
1∶5
10
1∶4
3. 选择。
(1) 无论什么样的图形,按一定的比放大或缩小后,与原来的图形相比,大小
( ),形状( )。
① 不变 ② 变了 ③ 无法确定
(2) 把一个长方形按1∶2的比缩小后,各条边的长都是原来的( )。
① 2倍 ② ③ 4倍 ④
(3) 下面描述的现象中,属于把图形放大的是( ),属于把图形缩小的是( )。
① 小明去照相馆拍了一张自己的2寸照片
② 李大爷用放大镜仔细地看报纸
③ 小红照哈哈镜
②
①
②
②
①
4. 按2∶1的比画出平行四边形放大后的图形;
按1∶2的比画出下面图形缩小后的图形。
5. 一个直角三角形的三条边的长度分别是6厘米、8厘米、10厘米,按一定的比放
大后,最长边长50厘米,另两条边分别长多少厘米?
50÷10=5 5×6=30(厘米) 5×8=40(厘米)
解析:先求出最长边之间的倍数关系,再求另两条边的长度。
第2课时 比例的意义
1. 填空。
(1) 表示( )叫作比例。
(2) 5∶2的比值是( ),∶的比值是( ),因为比值( ),所以这两
个比可以组成比例( )。
(3) 写出比值是的两个比,并将它们组成比例:(
)。
(4) 用20以内的四个合数组成一个比例是( )。
两个比相等的式子
相等
5∶2=∶
答案不唯一,如4∶5=
答案不唯一,如4∶6=12∶18
8∶10
2. 把能组成比例的钥匙和锁连起来。
3. 选择。
(1) 下面的式子中,( )是比例。
① 2.5∶1.5>20∶15 ② 2×6=3+9
③ 2.4∶3=0.8 ④ 48∶8=12∶2
(2) 下面的算式中,能与12∶11组成比例的是( )。
① 11∶12 ② 0.12∶1.1 ③ ∶ ④ ∶
(3) 下面的算式中,不能与∶4组成比例的是( )。
① 6∶15 ② 3∶20 ③ ∶ ④ 0.9∶6
④
④
①
4. 李师傅上午3小时加工零件240个,下午5小时加工零件400个。
(1) 比一比李师傅上午加工零件的个数和时间的比及下午加工零件的个数和时间
的比,这两个比能组成比例吗?如果能,写出来。
(2) 比一比李师傅上、下午加工零件个数的比和上、下午加工时间的比,这两个
比能组成比例吗?如果能,写出来。
5. 将下图中的长方形按3∶1的比放大,然后观察图中数据,你能根据图中数据写出
哪些比例?(写出2个即可)
图略 答案不唯一,如9∶3=6∶2 9∶6=3∶2
240∶3=80 400∶5=80 能 240∶3=400∶5
240∶400=0.6 3∶5=0.6 能 240∶400=3∶5
6. 如图,在线段AG中,AB=BC=CD=DE=EF=FG,你能根据它们间的长度,将下列
比例补充完整吗?
(1) AB∶BC=( )∶( )
(2) ( )∶( )=BG∶DG
(3) BC∶AE=( )∶( )
(4) ( )∶( )=BF∶AG
CD
DE
(答案不唯一)
AF
AD
CD
CG
AE
AG
7. 观察图①,照样子把图②按4∶1的比放大。
解析:按4∶1的比放大就是对应线段的长度是原长度的4倍。
第3课时 比例的基本性质
1. 填空。
(1) 如果1.4∶a=b∶7(a、b不为0),那么1.4×( )=( )×( )。
(2) 如果3a=5b(a、b不为0),那么a∶b=( )∶( )。
(3) =
(4) 在一个比例中,两个外项互为倒数,其中一个内项是10以内最大的合数,另
一个内项是( )。
(5) 如果甲的与乙的相等(甲、乙不为0),那么乙∶甲=( )∶( )。
(6) 在一个比例中,两个比的比值都是1.5,这个比例的两个外项分别是12和45,
这个比例是( )或( )。
(7) 在比例12∶45=8∶30中,如果第一个比的后项增加15,那么第二个比的前
项应该( )才能使比例成立。
7
a
b
5
3
(答案不唯一)
24
3
25
28
12∶8=67.5∶45
45∶30=18∶12
减少2
2. 判断。
(1) 用比例中两个外项的积减去两个内项的积,结果是0。 ( )
(2) 5∶4和∶可以组成比例。 ( )
(3) 在比例中交换两个外项的位置,比例依然成立。 ( )
(4) 因为4×6=3×8,所以4∶6=3∶8。 ( )
(5) 在比例中,两个外项不变,一个内项缩小为原来的,另一个内项扩大为原
来的3倍,比例依然成立。 ( )
3. 根据比例的基本性质判断哪组中的两个比可以组成比例,并把能组成的比例写
出来。
(1) ∶和∶ (2) ∶0.3和3.2∶
(1) ×= ×= ≠ 不能
(2) 0.3×3.2=0.96 ×=0.96 0.96=0.96 能 ∶0.3=3.2∶
√
√
×
√
√
4. 选择。
(1) 能与∶组成比例的是( )。
① ∶5 ② ∶ ③ 5∶4 ④ ∶
(2) 因为10∶5=3.6∶1.8,所以( )。
① 10×3.6=5×1.8 ② 5×10=1.8×3.6
③ 10×1.8=5×3.6 ④ 3.6÷5=10÷1.8
(3) 用、、30、24四个数组成的比例是( )。
① ∶=30∶24 ② ∶=30∶24
③ ∶24=∶30 ④ 30∶ =∶24
③
③
②
5. 把下面两组数组成的比例写出来。(写一个即可)
(1) 0.7、7、8和80
(2) 、、和
6. 在比例a∶b=c∶d中,a+d=38,d-a=22,a∶b与c∶d的比值均为,这个比
例是多少?
答案不唯一,如0.7∶7=8∶80
答案不唯一,如∶=∶
(38-22)÷2=8 8+22=30 8÷=5 30×=48 8∶5=48∶30
7. 已知a∶10=4∶b,那么ab+4的值是多少?
10×4=40 40+4=44 解析:根据比例的基本性质先求ab的值,再加4求出问题的答案。
第4课时 解比例
1. 填空。
(1) 妈妈手表上的一个零件长5毫米,把它按9∶1的比画在图上,零件在图上应
画( )厘米。
(2) 上海东方明珠塔高468米,江工程师按1∶200的比制作了一个模型,模型高
( )米。
2. 根据比例的基本性质,在括号里填合适的数。
15∶6=( )∶2 =
2.5∶5=( )∶20 ( )∶3.5=0.6∶7
4.5
2.34
5
10
0.3
( )
32
40
3. 解比例。
2.4∶0.25=6.4∶x x∶1.2=25∶7.5
= x∶0.3=
4. 根据条件写出比例,再解比例。
(1) x和8的比等于4和的比。
(2) 一个比例两个外项是1.25和1.6,两个内项是2.5和x。
x=
x=4
x=16
x=
x∶8=4∶ x=160
1.25×1.6=2.5x x=0.8
5. 把左边的平行四边形按比例缩小后得到右边的平行四边形,求未知数x。
6. 一个等腰三角形花圃的底和高的长度比是3∶2,底是24米,高是多少米?面积是
多少平方米?
7. 妈妈调制一杯蜂蜜水,400克水中放了20克蜂蜜。涛涛和妹妹想配制同样口味的
蜂蜜水,如果有600克水,需要放多少克蜂蜜?
6∶x=12∶8 x=4
设高是x米。 24∶x=3∶2 x=16
24×16÷2=192(平方米)
设需要放x克蜂蜜。 400∶20=600∶x x=30
8. 小刚家今年收向日葵吨,如果千克向日葵可榨油千克,这批向日葵共可榨油
多少千克?
设这批向日葵共可榨油x吨。∶=∶x x=0.14 0.14吨=140千克
9. 一个数,它能和、2、6组成比例,这个数可能是( ),组成的比例是(
);还可能是( ),组成的比例是( );还可能是( ),
组成的比例是( )。
∶6=
∶2
1
∶2=1∶6
36
2∶=36∶6
(比例答案不唯一)
解析:可以设这个数为x,根据比例的性质,列出方程,解出x。
第5课时 比例尺的意义
1. 填空。
(1) 比例尺表示( )和( )的比。
(2) 在比例尺是1∶8000000的地图上,图上距离是实际距离的 ,图
上1厘米表示实际距离( )千米。
(3) 杭州湾大桥全长大约是36千米。在一幅地图上量得杭州湾大桥的长是7.2厘
米,这幅地图的比例尺是( )。
(4) 在一张精密零件的图纸上,1厘米表示实际长度2毫米。这张图纸的比例尺是
( )。
(5) 把线段比例尺 改写成数值比例尺是( )。
(6) 一幅图的比例尺是1∶3000,如果改写成线段比例尺是( )。
图上距离
实际距离
( )
( )
1
8000000
80
1∶500000
5∶1
1∶6000
2. 判断。
(1) 比例尺是一个前项为1的比。 ( )
(2) 比例尺100∶1表示图上距离是实际距离的100倍。 ( )
(3) 有一幅图,图上2厘米表示实际距离150米,这幅图的比例尺是。 ( )
(4) 把线段比例尺 改写成数值比例尺是1∶9000000。 ( )
3. 选择。
(1) 一幅图上,图上距离6厘米表示实际距离24米,这幅图的比例尺是( )。
① 1∶4 ② 1∶400 ③ 400∶1
(2) 小东有一张长5厘米、宽3厘米的卡片。选比例尺( )画图最大,选比例尺
( )画图最小。
① 2∶1 ② 1∶2 ③ 1∶4
(3) 一幅图上,图上距离7分米表示实际距离7毫米,这幅图的比例尺是( )。
① 1∶1 ② 1∶100 ③ 100∶1
√
×
×
×
②
①
③
③
4. 从北京到杭州的实际距离大约是1200千米,在一幅地图上量得两地之间的距离是
6厘米,求这幅地图的比例尺。
5. 学校的操场长120米,宽 80米,下面是这个操场的平面图。量一量,求出这个平
面图的比例尺,并用线段比例尺表示出来。
6. 一只蚂蚁的实际长度是5mm,画在一幅图上的长是3cm,这幅图的比例尺是多少?
3 cm=30 mm
30∶5=6∶1
1200千米=120000000厘米 6∶120000000=1∶20000000
120米=12000厘米
3∶12000=1∶4000 图略
7. 一块长方形地的实际长是200米,宽是80米,小明在一幅平面图上画出的这块地
的长是10厘米,宽是8厘米,小明画得对吗?
200∶80=5∶2 10∶8=5∶4 5∶2≠5∶4 小明画得不对
解析:按比例放大和缩小只改变图形的大小,不改变形状,先分别求出两个长方形长与宽的比,再看比是否相同。
第6课时 比例尺的实际应用
1. 填表。
图上距离 实际距离 比例尺
20厘米 4千米
15厘米 1∶500000
12千米 1∶200000
30厘米 300∶1
1∶20000
75千米
1毫米
6厘米
2. 下面是光明小学校园的平面图。
(1) 图上1厘米的线段表示实际距离( )厘米。
(2) 量一量平面图中教学楼的长是( )厘米,宽是( )厘米。教学楼实际的
长是( )米,宽是( )米,占地面积是( )平方米。
3. 从一幅地图上量得宁通高速公路长4厘米,已知这幅地图的比例尺是1∶4000000。
宁通高速公路实际长多少千米?
4. 北京故宫是中国现存规模最大、保存最完整的古建筑群,占地呈长方形,南北
长约960米,东西宽约750米,把它画在比例尺是 1∶6000的图上,长和宽分别
是多少厘米?
1200
3
1
36
12
432
4×4000000=16000000(厘米)=160千米
960米=96000厘米 750米=75000厘米
长:96000÷6000=16(厘米) 宽:75000÷6000=12.5(厘米)
5.
(1) 鹏鹏家到学校的距离是1200米,图上距离是( )厘米,这幅图的比例尺是
( )。
(2) 在(1)的条件下,从学校到图书馆的图上距离是( )厘米,实际距离是
( )米。
6. 在比例尺为 的地图上,量得北京到南京的铁路长度是 14厘米,
一列高铁以每小时350千米的速度从南京开往北京,需要多少小时?
1
1∶120000
2
2400
75×14÷350=3(小时)
7. 在一幅比例尺为1∶20000的地图上,量得学校到游乐场的距离是15厘米,在另
一幅比例尺是的地图上,学校到游乐场的距离是多少厘米?
15×20000×=5(厘米)
8. 在比例尺是1∶20000000的地图上,A、B 两地相距4.5厘米,甲、乙两车同时从
A、B两地出发,以7∶8的速度相对开出,相遇时甲车比乙车少行多少千米?
20000000厘米=200千米 4.5×200÷(8+7)=60(千米)
解析:时间相同,速度比等于路程比,所以甲车与乙车行驶的路程比是7∶8,全程共15份,甲车正好比乙车少行1份,求出1份是多长就行。
第7课时 练 习 课
1. 填空。
(1) 4、5、10和另一个数可以组成一个比例,这个数可能是( )、( )或( )。
(2) 在一幅图上,量得A、B两个景点的图上距离是3厘米,A、B两个景点的实际
距离是900米,这幅图的比例尺是( )。
(3) 南京到上海的实际距离大约是300千米,画在一幅比例尺是1∶5000000的地
图上,应画( )厘米。
(4) 某个零件长2毫米,如果画在比例尺是25∶1的图纸上,应画( )厘米。
(5) 在比例尺是 的地图上,某段国道长20厘米,这段国道实际长
( )千米。如果在另一幅地图上,这段国道的长度扩大了2倍,另一幅图的
比例尺是( )。
2
8
12.5
1∶30000
6
5
800
1∶2000000
2. 判断。
(1) 由两个比组成的式子叫作比例。 ( )
(2) 为便于计算,比例尺前项或后项一般为1。 ( )
(3) 在比例中,两个外项的积与两个内项的积的比是1∶1。 ( )
(4) 在比例尺是20∶1的图上,实际距离是图上距离的20倍。 ( )
3. 解比例。
x∶= ∶3 0.06∶0.5=0.12∶x
√
√
×
×
x=
x=1
4. 下面是育才小学附近的平面图。
(1) 量出育才小学到新华书店的图上距离,再算出它们之间的实际距离。
(2) 超市在育才小学的正东方向3千米处,电影院在育才小学的正西方向2500米
处。算一算,并在图中标出超市和电影院的位置。
图上距离:1厘米 1×100000=100000(厘米)=1千米
3千米=300000厘米 300000÷100000=3(厘米)
2500米=250000厘米 250000÷100000=2.5(厘米) 图略
5. 下面是淘淘家与游乐园之间的路线图。
(1) 已知淘淘家与展览馆之间的实际距离是3千米。量一量,将图中比例尺补全。
(2) 妈妈准备带淘淘打的经过展览馆到游乐园。出租车3千米以内的收费为 9元,
以后每增加1千米的收费为2.4元。从家到游乐园打的需要多少元?
3÷1.5=2(千米) 图略
(1.5+4)×2=11(千米) (11-3)×2.4+9=28.2(元)
6. 如图,AD=8厘米,BE=12厘米,AC+BC=25厘米,三角形ABC的面积是多少?
BC×AD÷2=AC×BE÷2 BC×AD=AC×BE AC∶BC=AD∶BE
AC∶BC=8∶12=2∶3 25÷(2+3)×3=15(厘米)
15×8÷2=60 (平方厘米) 解析:可以根据三角形面积
的两种不同计算方法得到一个比例式,再求出AC与BC的比,接着根据AC与BC的和求出BC的长,最后求出三角形的面积。
第8课时 面积的变化
1. 填空。
(1) 如右图,量一量,算一算,大平行四边形与小平行四边形底
的比是( ),高的比是( ),面积的比是( )。
(2) 如果一个圆的半径扩大为原来的2倍,那么直径扩大为原来的( )倍,周
长扩大为原来的( )倍,面积扩大为原来的( )倍。
(3) 如果一幅建筑施工图的比例尺是 1∶1000,那么这幅建筑施工图的图上面
积与实际面积的比是( )。
(4) 如果把一个图形按1∶m的比缩小,缩小后与缩小前图形的面积比是( )。
2∶1
2∶1
4∶1
2
2
4
1∶1000000
1∶m2
2. 判断
(1) 将一个图形按一定的比放大或缩小后,图形中所有线段都按相同的比放大
或缩小了。 ( )
(2) 一个等边三角形放大后的面积是原来的25倍,高一定是原来的5倍。 ( )
(3) 在比例尺是1∶8的图纸上,甲、乙两个圆的半径比是2∶3,那么甲、乙两
个圆实际的半径比也是2∶3。 ( )
3. 选择。
(1) 把一张照片按5∶1的比放大,放大后和放大前照片的面积比是( )。
① 10∶1 ② 1∶25 ③ 25∶1
(2) 在比例尺是4∶1的图纸上,一朵胸花的实际面积是3平方厘米,图上面积是
( )平方厘米。
① 3 ② 12 ③ 48
(3) 如右图,将一个小正方体按 2∶1 的比放大,新的正方体与原
正方体表面积的比是( ),体积比是( )。
① 2∶1 ② 4∶1 ③ 8∶1
√
√
√
③
③
②
③
4. 有一块边长为60米的正方形草坪,在一幅比例尺是1∶2000的平面图上,这块草
坪的图上面积是多少?
5. 在一幅比例尺是 的校园平面图上,学校的操场如下图。(取整厘
米数)
(1) 量一量,算一算,求出操场的图上面积和实际面积。
(2) 写出图上面积与实际面积的比,并与比例尺进行比较,你发现了什么?
60米=6000厘米 6000÷2000=3(厘米) 3×3=9(平方厘米)
图上面积:2×3=6(平方厘米)
实际面积:(2×40)×(3×40)=9600(平方米)
9600平方米=96000000平方厘米 6∶96000000=1∶16000000
40米=4000厘米 12∶40002=1∶16000000
比例尺的平方等于图上面积与实际面积的比
6. 把一个面积是16平方厘米的正方形放大,放大后的正方形的面积是原来正方形面
积的9倍。放大后的正方形的边长是多少厘米?
16×9=144(平方厘米) 144=12×12 边长是12厘米
7. 将一个小圆放大成一个大圆,它们的面积之差是 209 cm2,小圆的周长是大圆周
长的。你能求出小圆的面积吗?
92∶102=81∶100 209÷(100-81)×81=891(cm2)
解析:面积比是长度比的平方,根据周长比为9∶10,先求出面积比为
81∶100,再利用面积差求出小圆面积。
满分:100分 时间:60分钟 得分:_____
第四单元自主检测
一、填空。(每空1分,共24分)
1. 从24的因数中选四个数,组成一个比例是( )。
2. 在2、3、4、5、6中去掉( ),剩下的四个数可组成比例。
3. 若∶x和12∶20能组成比例,则x等于( )。
4. 在5∶3=15∶9中,将3扩大为原来的5倍,9增加( ),比例仍然成立。
5. 将底是4厘米、高是3厘米的平行四边形按( )的比放大,可得到底是12厘米、
高是( )厘米的平行四边形,新的平行四边形和原图形的面积比是( )。
6. 将高100米、面积为5000平方米的梯形按1∶2000的比缩小,新梯形高( )厘米,
面积是( )平方厘米。
答案不唯一,如1∶2=12∶24
5
36
3∶1
9
9∶1
5
12.5
7. 一幅图的比例尺是 ,在这幅图上,图上距离是12厘米,实际距离
是( )千米,实际距离是225千米,图上距离是( )厘米。
8. 一幅图的图上距离4厘米表示实际距离2千米,这幅图的比例尺是( ),
一条16千米长的路画在这幅图上长( )。
9. 一种零件长5毫米,把它画在比例尺是10∶1的图上应画( )厘米,在这幅图上
量得另一种零件长7.2厘米,实际长( )毫米。
10. 在比例尺是的图上,量得一个正方形的面积是9平方厘米,它的实际面积是
( )平方米。
11. 完成下表:
540
5
1∶50000
32厘米
5
7.2
900
图上距离 实际距离 比例尺
2.4厘米 1∶4000
3厘米 420千米
4800千米 1∶50000000
9.6厘米
96米
1∶14000000
12. 用4、3、15和x可以组成比例,x最大是( ),x最小是( )。
13. 如右图,A、B两个图形重叠在一起,重叠部分的面积是A的,是B的
,A、B两个图形面积的比是( )。
14. 一个比例的两个内项是3和8,两个比的比值都是,这个比例是( )
或( )。
二、判断。(每题1分,共6分)
1. 一幅世界地图的比例尺是1∶50000。 ( )
2. 根据比例的基本性质可以解比例。 ( )
3. 将一个图形放大或缩小后,图形的大小改变,形状不变。 ( )
4. 如果一幅地图的比例尺是1∶500,那么图上面积与实际面积的比是1∶500。( )
5. 在同一幅图上,图上距离越长,实际距离也越长。 ( )
6. 如果5x=10y(x、y都不等于0),那么x∶y=2∶1。 ( )
20
2∶3
1∶3=8∶24
∶8=3∶9
√
√
×
√
√
×
三、选择。(每题1分,共6分)
1. 下面各比中,能与∶组成比例的是( )。
① 3∶4 ② 4∶3 ③ 4∶9 ④ 9∶4
2. 一幅地图的比例尺是 ,关于这个比例尺,下面表述正确的是( )。
① 图上距离是实际距离的
② 图上距离是实际距离的
③ 图上距离和实际距离的比是1∶900
④ 图上距离1千米表示实际距离30千米
3. 如果a<b<c<d(a≠0),且利用 a、b、c、d 四个数能组成比例,那么下面算式
( )可能是正确的。
① a∶b=d∶c ② b∶a=c∶d
③ a∶c=b∶d ④ c∶b=a∶d
③
②
③
4. 在两个圆中,它们的半径比与它们的( )不可以组成比例。
① 直径比 ② 周长比
③ 面积比 ④ 直径比或周长比
5. 一个电子零件的实际长度是2毫米,画在图纸上是4厘米,这张图纸的比例尺是
( )。
① 1∶20 ② 20∶1
③ 2∶1 ④ 1∶2
6. 红关小学新建一个长方形游泳池,长100米,宽50米。把它画在长15厘米、宽10
厘米的纸上,在下面各比例尺中,选用( )不合适。
① 1∶1000 ② 1∶500
③ 1∶2000 ④ 1∶5000
③
②
②
四、计算。(共18分)
1. 解比例。(12分)
x∶3=∶ = ∶x= ∶ 8∶x=
2. 将下图左边的三角形按比例缩小后得到右边的三角形,求未知数x。(3分)
3. 下图中小平行四边形放大后得到大平行四边形,求大平行四边形的高。(单位:
分米)(3分)
设大平行四边形的高为x分米。
12.8∶x=3.2∶1.2
x=4.8
3.2∶1.6=4.8∶x
x=2.4
x=
x=
x=
x=64
五、操作。(每题3分,共6分)
1. 按1∶3的比画出三角形缩小后的图形。
2. 按2∶1的比画出圆放大后的图形,并和原来的圆组成一个圆环。
六、解决问题。(共40分)
1. 有一幅中国地图。
(1) 这幅地图的比例尺是多少?(2分)
(2) 南京到上海的实际距离大约是320千米。在这幅地图上,南京到上海的距离
大约是多少厘米?(2分)
(3) 在这幅地图上,北京到广州的距离大约是48厘米,那么北京到广州的实际距
离大约是多少千米 (2分)
1∶5000000
5000000厘米=50千米 320÷50=6.4(厘米)
48×50=2400(千米)
2. 胡夫金字塔的高度是136.5米,如果按1∶10的比缩小,建造一座胡夫金字塔模型,
那么这座金字塔模型的高度是多少米?(5分)
3. 一张照片长4厘米,宽3厘米,如果按4∶1的比放大,放大后的长是多少厘米?如
果要使放大后的宽是15分米,就要按几比几放大?(5分)
4. 一种药水,药和水的比是3∶200。配置这种药水,270克药需加水多少千克?4吨
水需加药多少千克?(5分)
5. 甲、乙两地相距420千米,在一幅图上甲、乙两地的距离是6厘米,在这幅图上乙、
丙两地相距18厘米,乙、丙两地的实际距离是多少千米? (5分)
136.5÷10=13.65(米)
4×4=16(厘米) 15分米=150厘米 150∶3=50∶1
水:270÷3×200=18000(克)=18千克
药:4÷200×3=0.06(吨)=60千克
18÷6×420=1260(千米)
6. 在比例尺是1∶4000000的地图上量得A、B两地的距离是8厘米,一列汽车以每小
时100千米的速度从A地开往B地,几小时可以行完全程的?(4分)
7. 下图是某小学操场的平面图,这个操场长150米。求这幅平面图的比例尺,并在
括号里填合适的数,在方框里填合适的单位。这个操场的实际面积是多少平方
米?(5分)
8×4000000=32000000(厘米)=320千米 320×÷100=2.4(小时)
150÷5=30(米) 比例尺为1∶3000
3×30=90(米) 150×90=13500(平方米)
30
60
90
米
8. 新世纪农场有一个长方形果园,长 1500米,宽 1200米。先选择合适的比例尺,
在其后面的括号里画“√”,并计算出图上的长和宽,再画出这个果园的平面
图。(5分)
1∶3000( ) 1∶30000( ) 1∶300000( )
30000厘米=300米
长:1500÷300=5(厘米)
宽:1200÷300=4(厘米)
图略
√
