苏教版六年级下册数学 作业课件 第二单元 圆柱和圆锥 (共52张PPT)
文档属性
| 名称 | 苏教版六年级下册数学 作业课件 第二单元 圆柱和圆锥 (共52张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-13 15:12:59 | ||
图片预览







文档简介
(共52张PPT)
第二单元
二 圆柱和圆锥
第1课时 圆柱和圆锥的认识
1. 下面各图中,是圆柱的在括号里画“○”,是圆锥的在括号里画“△”。
○
△
○
2. 填空。
(1) 标出圆柱和圆锥各部分的名称。
(2) 圆柱从上到下( ),上、下两个底面是( )的圆,侧面是
一个( )。
(3) 圆锥有( )个顶点,底面是一个( )形,侧面是一个( )面。从圆锥
的( )到底面( )的距离是圆锥的高。
(4) 圆柱的高有( )条,圆锥的高有( )条。
( )
高
( )
侧面
( )
底面
( )
高
( )
底面
一样粗
两个相同
曲面
1
圆
曲
顶点
圆心
无数
1
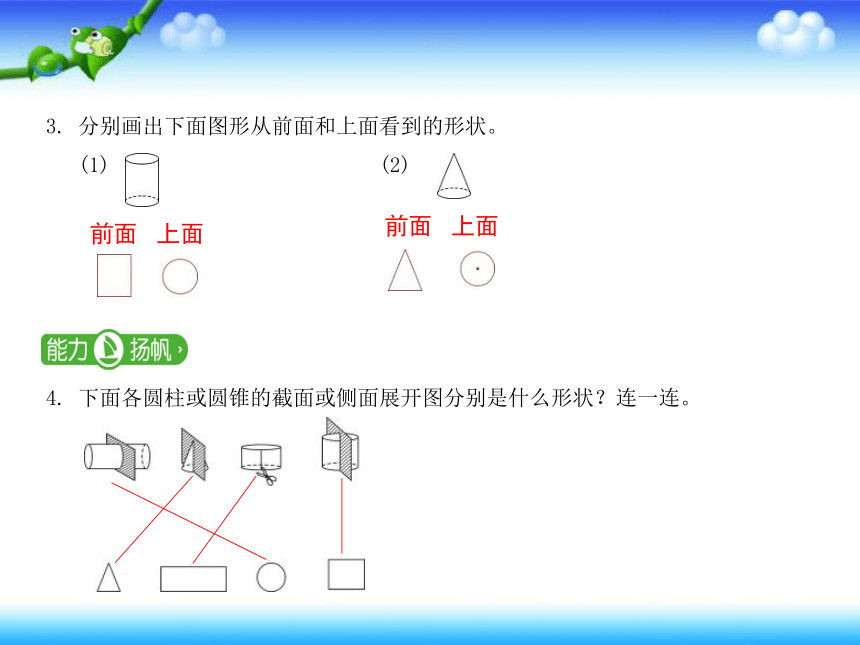
3. 分别画出下面图形从前面和上面看到的形状。
(1) (2)
前面
上面
前面
上面
4. 下面各圆柱或圆锥的截面或侧面展开图分别是什么形状?连一连。
5. 将下面的图形旋转后会得到什么图形?先想一想,再动手做一做,最后写出名称。
6. 蛋糕店用彩带捆扎一个圆柱形礼品盒(如图),如果打结部分用了30cm,那么捆扎
这个礼品盒至少需要多长的彩带?
40×4+20×4+30=270(cm)
圆锥 圆柱 上半部分是圆锥,下半部分是圆柱的组合体
7. 如下图,一个长方体的盒子里放了8个同样的易拉罐,每个易拉罐的底面直径是8
厘米,高是12.5厘米。这个长方体盒子的长、宽、高至少各是多少厘米?
长:8×4=32(厘米) 宽:8×2=16(厘米) 高:12.5厘米
解析:长方体盒子的长至少是4个直径长,宽至少是2个直径
长,高至少和易拉罐的高相等。
第2课时 圆柱的侧面积和表面积
1. 填空。
(1) 把圆柱的侧面沿着一条高展开,可以得到一个长方形,这个长方形的长等于
圆柱的( ),宽等于圆柱的( ),所以圆柱的侧面积
等于( )乘( )。
(2) 一个圆柱的底面直径是6厘米,高是5厘米,它的侧面积是( )平方厘米。
(3) 用一张长15厘米、宽10厘米的长方形纸围成一个圆柱,这个圆柱的侧面积是
( )平方厘米。
(4) 一个圆柱的侧面积是12.56平方分米,高是2分米,它的底面周长是( )
分米,底面积是( )平方分米,表面积是( )平方分米。
底面周长或高
高或底面周长
底面周长
高
30π
150
6.28
3.14
18.84
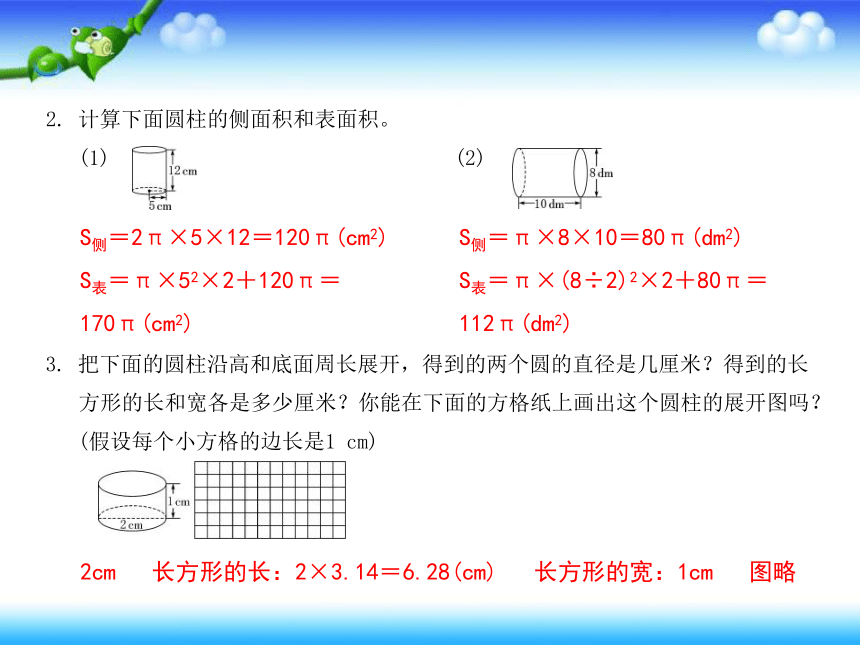
2. 计算下面圆柱的侧面积和表面积。
(1) (2)
S侧=2π×5×12=120π(cm2)
S表=π×52×2+120π=
170π(cm2)
S侧=π×8×10=80π(dm2)
S表=π×(8÷2)2×2+80π=
112π(dm2)
3. 把下面的圆柱沿高和底面周长展开,得到的两个圆的直径是几厘米?得到的长
方形的长和宽各是多少厘米?你能在下面的方格纸上画出这个圆柱的展开图吗?
(假设每个小方格的边长是1 cm)
2cm 长方形的长:2×3.14=6.28(cm) 长方形的宽:1cm 图略
4. 加油站有一个圆柱形油桶,高1.2米,底面半径是3分米。制作这个圆柱形油桶
至少需要铁皮多少平方分米?
5. 下图是一个圆柱形水池,水池的内壁和底面都要贴上瓷砖,水池的底面直径为
6米,池深1.2米。贴瓷砖的面积是多少平方米?
6. 一个圆柱的底面直径是2分米,将侧面沿高展开后正好是一个正方形。这个圆柱
的侧面积是多少平方分米?表面积是多少平方分米?
1.2米=12分米 3.14×3×2×12+3.14×32×2=282.6(平方分米)
3.14×6×1.2+3.14×(6÷2)2=50.868(平方米)
2×3.14×2×3.14=39.4384(平方分米)
39.4384+(2÷2)2×3.14×2=45.7184(平方分米)
7. 将一个棱长为2分米的正方体木料加工成一个最大的圆柱,圆柱的表面积是多少
平方分米?
(2÷2)2×3.14×2+3.14×2×2=18.84(平方分米)
解析:先寻找圆柱与正方体之间的关系:圆柱的直径、高和正方体的棱长相等,再根据已知条件求圆柱的表面积。
第3课时 练 习 课
1. 填空。
(1) 在表格里填上合适的数。
圆 柱 底面半径 3 cm
底面直径 8 dm
底面周长 6.28 m
高 6 cm 8 dm 10 m
侧面积
底面积
表面积
4 dm
1 m
6 cm
2 m
18.84 cm
25.12 dm
113.04 cm2
200.96 dm2
62.8 m2
28.26 cm2
50.24 dm2
3.14 m2
169.56 cm2
301.44 dm2
69.08 m2
(2) 王师傅要加工一根长2米,管口直径为2分米的圆柱形铁皮烟囱,至少需要铁皮( )平方米。
(3) 将直径是2厘米,高是5厘米的圆柱沿底面直径切成两个半圆柱后,表面积增加( )平方厘米。
1.256
20
2. 选择。
(1) 如果把圆柱的侧面沿高展开后得到一个正方形,那么圆柱的高等于( )。
① 底面直径 ② 底面直径的π倍 ③ 底面半径的π倍
(2) 圆柱的底面直径变成原来的2倍,高变成原来的,圆柱的侧面积( )。
① 是原来的2倍 ② 是原来的 ③ 不变
(3) 下面各图中,( )是圆柱的展开图。
① ② ③
(4) 如下图,将一个底面半径为 2分米、长1米的圆柱形木料截成 3个小圆柱后,
表面积增加( )平方分米。
① 4π ② 12π ③ 16π
②
③
②
③
3. 如下图,一辆压路机的滚筒是一个圆柱,它的长是2米,滚筒的横截面的直径是
1米。如果滚筒每分钟转5周,那么压路机每分钟能压路面多少平方米?
4. 王叔叔要做一对没有盖的圆柱形铁皮水桶,底面半径是2分米,高是10分米,做
这对水桶至少需要多少平方分米的铁皮?
5. 大厅内有8根同样的圆柱形支撑柱,每根高5米,底面周长是3.14米。如果每千克
油漆可漆2平方米,那么给这些支撑柱的表面刷油漆,需要油漆多少千克?
1×3.14×2×5=31.4(平方米)
(3.14×2×2×10+3.14×22)×2=276.32(平方分米)
3.14×5×8÷2=62.8(千克)
6. 把一个大圆柱截成两个小圆柱,两个小圆柱的高分别是4厘米和6厘米,它们的
表面积相差50.24平方厘米,原来大圆柱的表面积是多少?
50.24÷(6-4)=25.12(厘米)
(25.12÷3.14÷2)2×3.14×2+25.12×(4+6)=351.68(平方厘米) 解析:两个小圆柱的上、下底面面积相等,所以表面积差就是侧面积差,先用侧面积差÷高的差求出底面周长,再求表面积。
第4课时 圆柱的体积
1. 填空。
(1) 如右图,将一个圆柱切拼成一个长方体。长方体的底面积
等于圆柱的( ),长方体的高等于圆柱的( ),长方
体的体积等于( ),所以圆柱的体积也等于( )。
(2) 一个圆柱形钢坯的底面积是1.57平方分米,高是1米,体积是( )立
方分米。
(3) 一个圆柱形米桶,从里面量,底面周长是12.56分米,高是5分米,这个米
桶的容积是( )立方分米。
底面积
高
底面积×高
底面积×高
15.7
62.8
2. 判断。
(1) 一个圆柱和一个长方体的底面积和高都相等,圆柱的体积大一些。 ( )
(2) 表面积相等的两个圆柱,体积一定也相等。 ( )
(3) 把底面半径为4厘米,高为6厘米的圆柱切拼成体积相等的长方体,长方体
的表面积增加24平方厘米。 ( )
3. 计算下面各圆柱的体积。
(1) (2)
π×(6÷2)2×6=54π(dm3)
π×22×8=32π(cm3)
×
×
×
4. 一款圆柱形瓶装蜂蜜,小明从外面量,底面周长为 31.4厘米,高为12厘米。小
明认为蜂蜜量不实,生产商欺骗了消费者,他说的对吗?
5. 一个圆柱形蓄水池,底面直径是8米,高是2米,池内水深1.5米。这个圆柱形蓄
水池已蓄水多少立方米?
6. 李师傅将一个棱长为8分米的正方体削成一个最大的圆柱,圆柱的体积是多少?
(31.4÷3.14÷2)2×3.14×12=942(立方厘米)
942立方厘米=942毫升 942<950 对
(8÷2)2×3.14×1.5=75.36(立方米)
3.14×(8÷2)2×8=401.92(立方分米)
7. 把一个高5分米的圆柱的底面分成许多相等的扇形,然后把圆柱切开,再拼成一
个近似的长方体,表面积增加了40平方分米。圆柱的体积是多少立方分米?
40÷2÷5=4(分米) π×42×5=80π(立方分米)
解析:如图,表面积比原来增加的面积是左、右两个长方形的面积,长方形的一条边是圆柱的半径,与它相邻的另一条边是圆柱的高,增加的面积先除以2再除以高就可以求出圆柱的半径,再求体积即可。
第5课时 练 习 课(1)
1. 填空。
(1) 一个圆柱的底面半径是4分米,高是5分米,体积是( )立方分米。
(2) 强强家有一个底面积是15平方分米、高是6分米的圆柱形木质米桶,木材的
厚度不计,这个米桶的容积是( )立方分米,每升米重0.75千克,这个米桶
最多可装米( )千克。
(3) 挖一个底面周长是6.28米的圆柱形蓄水池,要使蓄水池能蓄水15.7立方米,
这个蓄水池要挖( )米深。
(4) 一个圆柱形玻璃水缸的底面周长是125.6厘米,水缸内有15厘米深的水,将
一块石头浸没在水中,水面上升到17厘米,这块石头的体积是( )立方厘
米。
80π
90
67.5
5
2512
2. 选择。
(1) 一个圆柱,高缩小为原来的,底面半径扩大为原来的2倍,体积( )。
① 不变 ② 扩大为原来的2倍 ③ 扩大为原来的4倍
(2) 一个长方体和一个圆柱的底面周长、高都相等,对比它们的体积,( )。
① 长方体的体积大 ② 圆柱的体积大
③ 长方体和圆柱的体积一样大
(3) 如下图,将底面直径为8厘米的圆柱切拼成长方体,表面积增加80平方厘米。
长方体的体积是( )立方厘米。
① 40π ② 160π
③ 320π
(4) 将一个高是 2 dm的圆柱按 2∶3 的体积比截成两个小圆柱后,表面积增加
50.24 cm2,截成后较小的小圆柱的体积是( )。
① 50.24cm3 ② 200.96cm3 ③ 301.44cm3
②
②
②
②
3. 一个自来水管的内直径是2厘米,管内的水流速度是每秒8厘米,如果一个自来水
管忘了关,5分钟会浪费多少升水?
4. 如下图,一个长方形长8分米,宽6分米。将它绕着边AB旋转一周,形成圆柱,该
圆柱的体积是多少立方分米?
5. 一个注满水的圆柱形容器的底面积是18平方分米,高是2分米,现将一个底面积
是10平方分米,高是2.5分米的圆柱形石柱垂直插入容器中,最多会有多少升水
溢出?
(2÷2)2×3.14×8×60×5=7536(立方厘米)=7.536升
π×6×6×8=288π(立方分米)
10×2=20(立方分米)=20升
6. 一个饮料瓶的瓶身如下图,饮料瓶的容积是3立方分米。它里面有一些饮料,正
放时饮料的高度为20厘米,倒放时空余部分的高度为5厘米。瓶内的饮料有多少
立方分米?
20∶5=4∶1
3÷(4+1)×4=2.4(立方分米)
解析:两个瓶中空余部分的体积相等,所以饮料的体积与空余部分的体积比为20∶5=4∶1,接着根据饮料瓶的容积和体积比求出饮料体积。
第6课时 练 习 课(2)
1. 填空。
(1) 一个圆柱的底面周长是94.2厘米,高是10厘米。它的表面积是( )平
方厘米,体积是( )立方厘米。
(2) 将棱长为4分米的正方体铁块熔铸成底面积是32平方分米的圆柱,圆柱的高
是( )分米。
(3) 填表。
2355
7065
2
圆 柱 底面 半径 底面 直径 底面积 高 表面积 体 积
2 cm 5 cm
10 dm 6 dm
4 cm
4π cm2
28π cm2
20π cm3
5 dm
25π dm2
110π dm2
150π dm3
2. 选择。
(1) 两个高相等的圆柱,底面的直径比是1∶3,则它们的体积比是( )。
① 1∶3 ② 1∶6 ③ 1∶9
(2) 乐乐有两张长18.84厘米、宽12.56厘米的长方形纸,他将它们分别卷成高
18.84厘米和12.56厘米的两个圆柱,这两个圆柱的体积相比,( )。
① 一样大 ② 高18.84厘米的体积大
③ 高12.56厘米的体积大
(3) 一个圆柱形水桶的容积是50升,底面积是20平方分米。若桶内盛水80%,则
水面距桶口( )分米。
① 0.5 ② 2 ③ 2.5
(4) 如下图,一张铁皮剪下图中阴影部分,正好可以做一个底面直径为4分米的
圆柱形油桶,这个油桶的容积是( )立方分米。
① 32π ② 64π ③ 16π2
③
③
①
①
3. 做一个底面半径是3分米,高是5分米的圆柱形无盖铁桶。
(1) 做这样一个铁桶至少需要多少平方分米的铁皮?
(2) 如果用这个铁桶盛水,那么最多能盛水多少升?
(3) 若将这些水倒入一个长6分米、宽5分米、高5分米的长方体水槽中,则水面
高多少分米?
4. 如下图,有一个长 2米、底面直径为0.8米的圆木,一半浮出水面,一半浸入水
中,圆木浸入水中的表面积、体积各是多少?
表面积:(0.8÷2)2×3.14+3.14×0.8×2÷2=3.0144(平方米)
体积:(0.8÷2)2×3.14×2÷2=0.5024(立方米)
3.14×3×2×5+3.14×32=122.46(平方分米)
3.14×32×5=141.3(立方分米) 141.3立方分米=141.3升
141.3÷(6×5)=4.71(分米)
5. 佳佳的生日蛋糕有两层,每层高0.5分米,底面直径分别是4分米、3分米。在这
个蛋糕的表面平均每平方分米抹40克奶油,制作这个蛋糕共需奶油多少克?
[4×3.14×0.5+3×3.14×0.5+(4÷2)2×
3.14]×40=942(克)
解析:蛋糕朝上的面合起来正好是一个圆,所以抹奶油的面积是直径分别为4分米、3分米,高为0.5分米的两个圆柱的侧面积加一个直径为4分米的圆的面积。
第7课时 圆锥的体积
1. 填空。
(1) 右图中的圆柱和圆锥等底等高,则圆柱的体积是圆锥的
( ),圆锥的体积是圆柱的( )。
(2) 一个圆锥和一个圆柱等底等高,若圆锥的体积是18立方分米,则圆柱的体
积是( )立方分米。若圆柱的体积是18立方分米,则圆锥的体积是( )立
方分米。
(3) 一个圆锥的底面直径是8米,高是3米。这个圆锥的占地面积是( )平
方米,体积是( )立方米。
(4) 一个圆锥的体积是20立方米,高是6米,它的底面积是( )平方米。
3倍
54
6
16π
16π
10
2. 判断。
(1) 圆柱的体积大于圆锥的体积。 ( )
(2) 圆锥的体积是和它等底等高的圆柱体积的。 ( )
(3) 一个圆柱比和它等底等高的圆锥体积大。 ( )
(4) 体积比是1∶3的圆锥和圆柱一定等底等高。 ( )
3. 计算圆锥的体积。
(1) (2)
×9×3.6=10.8(m3)
π×32×12×=36π(cm3)
√
×
×
×
4. 李阿姨有一个圆锥形斗笠,底面周长是12.56分米,高是3分米。这个斗笠的占
地面积是多少?体积是多少?
5. 小天把一个底面半径是1分米,高是3分米的圆锥形铝块放入一个有水的圆柱形
容器内(铝块完全浸没在水中,且水没溢出),容器内的水将上升多少立方分米?
6. 王师傅有一个圆锥形零件,底面积是36平方厘米,高是 9厘米。这个零件的体
积是多少立方厘米?如果将它熔铸成和它高相等的圆柱,那么圆柱的底面积是
多少?
12.56÷3.14÷2=2(分米) 占地面积:3.14×22=12.56(平方分米) 体积:12.56×3× =12.56(立方分米)
1×1×3.14×3÷3=3.14(立方分米)
体积:36×9÷3=108(立方厘米)
底面积:108÷9=12(平方厘米)
7. 将一个底面直径是2分米的圆锥形木料沿着高切成相等的两部分,表面积增加了
12平方分米。原来圆锥的体积是多少立方分米?
12÷2×2÷2=6(分米) (2÷2)2×3.14×6÷3=6.28(立方分米)
解析:表面积增加的是两个三角形的面积,三角形的底等于圆锥的直径,高等于圆锥的高。 增加的面积÷2=一个三角形的面积,一个三角形的面积×2÷直径=圆锥的高,然后求体积。
第8课时 练 习 课
1. 填空。
(1) 建筑工人使用的一种圆锥形铜锤,底面半径是3厘米,高是6厘米。每立方
厘米铜重8.9克,这个铜锤的体积是( )立方厘米,质量是( )克。
(2) 等底等高的圆柱和圆锥的体积相差300立方厘米,那么圆锥的体积是(
),圆柱的体积是( )。
(3) 一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积
是24立方分米,圆柱的体积是( )立方分米。
(4) 一辆货车的车厢是一个长方体,它的长是4米,宽是2.5米,高是2米,装满
一车厢沙子,卸下后的沙堆是一个高2米的圆锥。沙堆的底面积是( )。
56.52
503.028
150
立方厘米
450立方厘米
24
30平方米
2. 选择。
(1) 把一个圆柱形木料削成一个最大的圆锥,圆锥的体积是60立方厘米,削去
的体积是( )立方厘米。
① 20 ② 120 ③ 180
(2) 体积相等、高相等的圆锥和圆柱,圆锥的底面积是圆柱底面积的( )。
① ② 3倍 ③ 9倍
(3) 高和底面积相等的圆锥和长方体,圆锥体积是30 m3,长方体体积( )。
① 是60 m3 ② 是90 m3 ③ 大于90 m3
(4) 如下图,小陶在一个圆柱形容器里装满雪后,又压进一个与圆柱形容器等
底等高的圆锥形木块,压过后雪的体积是( )cm3。
① 64π ② 128π ③ 192π
②
②
②
②
3. 如下图,有一个直角三角形,如果将它绕着最长的直角边旋转可以得到一个圆
锥,这个圆锥的体积是多少?
4. 一个修路队把一堆底面半径是3米,高是1.5米的圆锥形砂石铺在10米宽的公路
上,若铺2厘米厚,能铺多少米长?
5. 如下图,一个粮仓由一个圆柱和一个圆锥组成。如果每立方米粮食约重200千克,
这个粮仓大约可盛粮食多少吨?
[(4÷2)2×3.14×2+(4÷2)2×3.14×1.5÷3]×200=6280(千克)=6.28吨
9×9×π×12÷3=324π(cm3)
2厘米=0.02米
32×3.14×1.5÷3÷(10×0.02)=70.65(米)
6. 一个圆柱和一个圆锥的底面积之比是1∶2,体积之比是5∶4。如果圆柱高30厘
米,那么圆锥高多少厘米?如果圆锥高30厘米,那么圆柱高多少厘米?
(5÷1)∶(4×3÷2)=5∶6
圆锥的高:30÷5×6=36(厘米)
圆柱的高:30÷6×5=25(厘米)
解析:可以先根据底面积和体积的比求出圆柱和圆锥高的比,再解答问题。
第9课时 整理与练习(1)
1. 填空。
(1) 一个圆柱的底面周长是6.28分米,高是3分米,这个圆柱的侧面积是( )
平方分米,表面积是( )平方分米。
(2) 一个圆柱的底面积是1.5平方分米,高是 6分米,和它等底等高的圆锥的体
积是( )立方分米。
(3) 做10节底面直径是8分米、高是10分米的圆柱形铁皮烟囱,需要铁皮( )
平方米。
(4) 有一个底面积是60平方分米、高是9分米的圆柱形钢坯,若熔铸成底面积是
60平方分米的圆锥形钢坯,则圆锥的高是( )分米;若熔铸成高是9分米的圆
锥形钢坯,则圆锥的底面积是( )平方分米。
18.84
25.12
3
25.12
27
180
2. 选择。
(1) 并排放的等底等高的圆锥和圆柱从不同方向看到的不同形状如图,从上面看
到的形状是( ),从左面看到的形状是( )。
① ② ③
(2) 下面的图以虚线为轴旋转,可以得到圆锥的是( )。
① ② ③
(3) 将圆柱的侧面沿一条直线剪开,不可能得到( )。
① 平行四边形 ② 长方形 ③ 梯形
(4) 底面积为6.28平方分米,高为3分米的圆柱内装有一半的水,现将一个和它
等底等高的圆锥放入其中,水面高( )。
① 正好是1.5分米 ② 正好是2.5分米 ③ 低于2.5分米,高于1.5分米
②
③
②
③
③
3. 妈妈的茶杯(如右图)放在桌上,底面直径是8厘米,高是15厘米。
(1) 这只茶杯占据桌面的面积是多少平方厘米?
(2) 茶杯中部有一圈隔热塑料,这圈隔热塑料宽3厘米,这圈隔热塑料的面积是
多少平方厘米
(3) 这只茶杯的容积是多少立方厘米?(茶杯厚度忽略不计)
4. 王叔叔加工了一个零件(如下图),你能计算出它的体积吗?
π×(2÷2)2×3÷3+π×(2÷2)2×
4=5π(dm3)
3.14×(8÷2)2=50.24(平方厘米)
3.14×8×3=75.36(平方厘米)
50.24×15=753.6(立方厘米)
5. 如图所示的长方体盒子里有一个圆柱,这个圆柱的体积最大是多少立方分米?
(结果保留π)
(6÷2)2 ×π×4=36π(dm3)
(4÷2)2 ×π×6=24π(dm3)
(4÷2)2 ×π×8=32π(dm3)
24π<32π<36π 最大是36π dm3
解析:圆柱有三种摆放情况,可以先画出三种底面,再想高,分别是d=6 dm,h=4 dm;d=4 dm,h=6 dm;d=4 dm,h=8 dm,然后依次求体积,最后选最大的。
第10课时 整理与练习(2)
1. 填空。
(1) 一个直角三角形的两条直角边分别长 6厘米和8厘米。将它绕一条直角边旋
转,所得圆锥的体积是( )立方厘米或( )立方厘米。
(2) 将底面周长是6.28分米的圆柱的高增加4分米,表面积增加(
),体积增加( )。
(3) 将一个圆柱沿直径切开,得到边长是8厘米的正方形切面,原来圆柱的表面
积是( )平方厘米,体积是( )立方厘米。
96π
128π
25.12平方分
米
12.56立方分米
96π
128π
2. 判断。
(1) 一个长方体和一个圆锥的体积相等,底面积也相等,则圆锥的高是长方体
高的3倍。 ( )
(2) 底面周长和高都相等的圆柱和长方体,圆柱的体积比长方体大。 ( )
(3) 将一个直径4厘米、高5厘米的圆柱切拼成和它等底等高的长方体,体积不
变,表面积增加20平方厘米。 ( )
(4) 等底等高的圆柱体积比圆锥大200%。 ( )
3. 李大爷要挖一口深15米,底面半径是4分米的水井。
(1) 挖这口水井,需挖土多少立方米?
(2) 水井外有一堆底面周长是3.14米,高0.6米的圆锥形砂石,将这堆砂石填入
井底,能铺多厚?(得数保留一位小数)
4分米=0.4米 0.42×3.14×15=7.536(立方米)
(3.14÷3.14÷2)2×3.14×0.6÷3÷(0.42×3.14)≈0.3(米)
√
√
√
√
4. 制作一个无盖的圆柱形水桶,有下图①②③④四种型号的铁皮可供选择。应选
择哪几号?所制作的水桶的表面积和容积各是多少?(铁皮厚度忽略不计)
5. 一听苹果汁的底面直径是6厘米,高是10厘米,现做一个纸箱来包装。(如下图)
(1) 做这个纸箱至少需要多少平方厘米的硬纸板?(箱盖折出的边缘和接头处忽
略不计)
(2) 这个长方体纸箱的体积是多少?
选择②号和③号
表面积:12.56×3+3.14×22=50.24(dm2)
容积:3.14×22×3=37.68(dm3)
长:6×6=36(厘米) 宽:4×6=24(厘米)
(36×24+36×10+24×10)×2=2928(平方厘米)
36×24×10=8640(立方厘米)
6. 王师傅将一根圆柱形木料削去一块后,变成下图的形状。你能求出它现在的体
积是多少吗?
π×(6÷2)2=9π(平方分米)
(13+7)×9π÷2=90π(立方分米)
解析:如图,解答此题时可以采用转化法,再增加一个一样的图形,使它变成一个规则的圆柱,求出体积后再除以2。
满分:100分 时间:60分钟 得分:_____
第二单元自主检测
一、填空。(每空1分,共24分)
1. 0.73立方米=( )立方分米 280毫升=( )升
2. 一个圆柱的底面半径是8厘米,高是20厘米,它的侧面积是( )平方厘米,
表面积是( )平方厘米,体积是( )立方厘米。
3. 一个圆锥的底面直径是6分米,高是底面直径的2倍,它的高是( )分米,底
面积是( )平方分米,体积是( )立方分米。
4. 一个圆柱和一个圆锥等底等高,如果圆柱的体积是 48立方米,那么圆锥的体积
是( )立方米;如果圆锥的体积比圆柱少 2.4立方分米,那么圆柱的体积是
( )立方分米。
730
0.28
320π
448π
1280π
12
9π
36π
16
3.6
5. 在一个棱长为4分米的正方体容器中装满水,再将水全部倒入一个高是8分米的圆
锥体容器中,正好倒满,圆锥的底面积是( )平方分米。
6. 圆柱的高不变,底面半径扩大为原来的3倍,侧面积扩大为原来的( )倍,体积
扩大为原来的( )倍。
7. 一个圆柱的底面直径是2分米,高是5分米,如果沿着底面直径分成两个同样的半
圆柱,表面积增加( )平方分米,如果分成3个同样的小圆柱,表面积增加
( )平方分米。
8. 如图,把圆柱切拼成一个近似的长方体。
(1) 长方体的前、后两个面的面积之和就是圆柱的( )。
(2) 如果圆柱的侧面积是62.8平方厘米,底面半径是2厘米,那么这个圆柱的体
积是( )立方厘米。
24
3
9
20
4π
侧面积
62.8
9. 一个圆柱高10厘米,若把它的高截短了3厘米,则表面积就减少了942平方厘米,
这个圆柱的底面积是( )平方分米,体积是( )立方分米。
10. 将一个底面边长是4分米,高是5分米的长方体木料加工成一个最大的圆柱,圆
柱的体积是( )立方分米。
11. 一个蔬菜大棚如下图,这个蔬菜大棚占地( )m2,覆盖大棚的塑料薄膜的
面积是( )m2,整个大棚内的空间是( )m3。
12. 一个圆柱和一个圆锥的底面半径的比是3∶4,高的比是2∶3,圆柱与圆锥的体
积比是( )。
78.5
78.5
20π
100
176.625
196.25
9∶8
二、判断。(每题1分,共5分)
1. 圆柱和圆锥的高都有无数条。 ( )
2. 圆锥的侧面展开图是一个三角形。 ( )
3. 底面积相等的圆锥和圆柱的体积比是1∶3。 ( )
4. 如果一个圆柱和长方体的底面周长和高都相等,那么长方体的表面积比圆柱的表
面积小。 ( )
5. 底面半径为r分米,高为h分米的圆柱的表面积是2πr(h+r)平方分米。 ( )
三、选择。(每题1分,共5分)
1. 求一个圆柱形水桶能装多少升水,就是求这个水桶的( )。
① 侧面积 ② 表面积 ③ 体积 ④ 容积
2. 如果一个圆柱的侧面展开图正好是一个正方形,那么这个圆柱的高和它底面直径
的比是( )。
① 1∶1 ② 1∶π ③ π∶1 ④ 1∶πd
×
×
√
√
×
④
③
3. 一张长12.56分米、宽3.14分米的长方形铁皮不能和( )分米的圆配成圆柱。
① 半径为0.5 ② 直径为1
③ 直径为4 ④ 周长为9.42
4. 将一个长方形绕下面不同的虚线旋转,旋转后体积最大的是( )。
① ② ③ ④
5. 如下图,将棱长相等的两块正方体木料A、B分别加工成1个和4个圆柱,剩下的木
料体积相比,( )。
① A大 ② B大
③ 一样大 ④ 无法确定
④
③
④
四、细心观察,正确操作。(每题3分,共6分)
1. 在方格纸上画出下面无盖圆柱体的表面展开图。
2. 在已有的底面的基础上画出高1厘米的圆锥。
五、看图列式计算。(共17分)
1. 计算下面各图形的表面积。(单位:厘米)(6分)
(1) (2)
2. 计算下面各图形的体积。(单位:厘米)(6分)
(1) (2)
3. 如下图,一个直角三角形以虚线为轴旋转一周,得到一个圆锥,它的体积是多少
立方厘米?(5分)
π×42×2+π×4×2×
5=72π(平方厘米)
π×(2÷2)2×2+π×2×
10=22π(平方厘米)
π×22×6×=8π(立方厘米)
π×(6÷2)2×9=81π(立方厘米)
π×32×4× =12π(立方厘米)
六、解决问题。(共43分)
1. 用塑料绳捆扎一个圆柱形蛋糕盒(如下图),打结处正好是底面圆心,打结用去塑
料绳25厘米。
(1) 捆扎这个蛋糕盒至少要用去塑料绳多少厘米?(3分)
(2) 在它的整个侧面贴上一圈商标纸,商标纸的面积至少是多少平方厘米?(3分)
(3) 这个蛋糕盒所占的空间是多少立方分米?(3分)
2. 砌一个圆柱形污水处理池,底面周长是18.84米,深3米。在处理池的周围和底面
抹上水泥。
(1) 抹水泥的面积是多少平方米?(4分)
(2) 这个污水处理池最多可以容纳污水多少立方米?(4分)
4×50+4×15+25=285(厘米)
50×3.14×15=2355(平方厘米)
(50÷2)2×3.14×15=29437.5(立方厘米)=29.4375立方分米
18.84×3+(18.84÷3.14÷2)2×3.14=84.78(平方米)
(18.84÷3.14÷2)2×3.14×3=84.78(立方米)
3. 一个圆锥形沙堆的底面半径是2米,高是1.8米。每立方米沙约重1.5吨,这堆沙
约重多少吨?(5分)
4. 一个圆柱形水桶的容积是20立方分米,里面装了的水。已知水桶的底面积是6平
方分米,水面高多少分米?(5分)
5. 小明为了测量出一个土豆的体积,按如下步骤进行了一个实验:在一个底面直径
是8厘米的圆柱形玻璃杯中装入一定量的水,量得水面的高度是5厘米;将土豆放
入水中,再次量得水面的高度是7厘米。如果玻璃的厚度忽略不计,那么这个土
豆的体积大约是多少立方厘米?(5分)
3.14×(8÷2)2×(7-5)=100.48(立方厘米)
×3.14×22×1.8×1.5=11.304(吨)
20×÷6= (分米)
6. 如图,一个沙漏由两个圆锥组成,每个圆锥底面半径是 6厘米,高是10厘米。沙
漏里的沙子正好可以填满一个圆锥。沙漏里沙子的体积是多少?如果每分钟漏掉
20立方厘米的沙子,沙漏里的沙子从一头漏到另一头要多少分钟?(6分)
7. 如下图,阴影部分的材料正好可以做成一个圆柱,求这个圆柱的体积。(5分)
3.14×62×10÷3=376.8(立方厘米) 376.8÷20=18.84(分钟)
12.56÷3.14÷2=2(分米)
2×4=8(分米)
3.14×22×8=100.48(立方分米)
第二单元
二 圆柱和圆锥
第1课时 圆柱和圆锥的认识
1. 下面各图中,是圆柱的在括号里画“○”,是圆锥的在括号里画“△”。
○
△
○
2. 填空。
(1) 标出圆柱和圆锥各部分的名称。
(2) 圆柱从上到下( ),上、下两个底面是( )的圆,侧面是
一个( )。
(3) 圆锥有( )个顶点,底面是一个( )形,侧面是一个( )面。从圆锥
的( )到底面( )的距离是圆锥的高。
(4) 圆柱的高有( )条,圆锥的高有( )条。
( )
高
( )
侧面
( )
底面
( )
高
( )
底面
一样粗
两个相同
曲面
1
圆
曲
顶点
圆心
无数
1
3. 分别画出下面图形从前面和上面看到的形状。
(1) (2)
前面
上面
前面
上面
4. 下面各圆柱或圆锥的截面或侧面展开图分别是什么形状?连一连。
5. 将下面的图形旋转后会得到什么图形?先想一想,再动手做一做,最后写出名称。
6. 蛋糕店用彩带捆扎一个圆柱形礼品盒(如图),如果打结部分用了30cm,那么捆扎
这个礼品盒至少需要多长的彩带?
40×4+20×4+30=270(cm)
圆锥 圆柱 上半部分是圆锥,下半部分是圆柱的组合体
7. 如下图,一个长方体的盒子里放了8个同样的易拉罐,每个易拉罐的底面直径是8
厘米,高是12.5厘米。这个长方体盒子的长、宽、高至少各是多少厘米?
长:8×4=32(厘米) 宽:8×2=16(厘米) 高:12.5厘米
解析:长方体盒子的长至少是4个直径长,宽至少是2个直径
长,高至少和易拉罐的高相等。
第2课时 圆柱的侧面积和表面积
1. 填空。
(1) 把圆柱的侧面沿着一条高展开,可以得到一个长方形,这个长方形的长等于
圆柱的( ),宽等于圆柱的( ),所以圆柱的侧面积
等于( )乘( )。
(2) 一个圆柱的底面直径是6厘米,高是5厘米,它的侧面积是( )平方厘米。
(3) 用一张长15厘米、宽10厘米的长方形纸围成一个圆柱,这个圆柱的侧面积是
( )平方厘米。
(4) 一个圆柱的侧面积是12.56平方分米,高是2分米,它的底面周长是( )
分米,底面积是( )平方分米,表面积是( )平方分米。
底面周长或高
高或底面周长
底面周长
高
30π
150
6.28
3.14
18.84
2. 计算下面圆柱的侧面积和表面积。
(1) (2)
S侧=2π×5×12=120π(cm2)
S表=π×52×2+120π=
170π(cm2)
S侧=π×8×10=80π(dm2)
S表=π×(8÷2)2×2+80π=
112π(dm2)
3. 把下面的圆柱沿高和底面周长展开,得到的两个圆的直径是几厘米?得到的长
方形的长和宽各是多少厘米?你能在下面的方格纸上画出这个圆柱的展开图吗?
(假设每个小方格的边长是1 cm)
2cm 长方形的长:2×3.14=6.28(cm) 长方形的宽:1cm 图略
4. 加油站有一个圆柱形油桶,高1.2米,底面半径是3分米。制作这个圆柱形油桶
至少需要铁皮多少平方分米?
5. 下图是一个圆柱形水池,水池的内壁和底面都要贴上瓷砖,水池的底面直径为
6米,池深1.2米。贴瓷砖的面积是多少平方米?
6. 一个圆柱的底面直径是2分米,将侧面沿高展开后正好是一个正方形。这个圆柱
的侧面积是多少平方分米?表面积是多少平方分米?
1.2米=12分米 3.14×3×2×12+3.14×32×2=282.6(平方分米)
3.14×6×1.2+3.14×(6÷2)2=50.868(平方米)
2×3.14×2×3.14=39.4384(平方分米)
39.4384+(2÷2)2×3.14×2=45.7184(平方分米)
7. 将一个棱长为2分米的正方体木料加工成一个最大的圆柱,圆柱的表面积是多少
平方分米?
(2÷2)2×3.14×2+3.14×2×2=18.84(平方分米)
解析:先寻找圆柱与正方体之间的关系:圆柱的直径、高和正方体的棱长相等,再根据已知条件求圆柱的表面积。
第3课时 练 习 课
1. 填空。
(1) 在表格里填上合适的数。
圆 柱 底面半径 3 cm
底面直径 8 dm
底面周长 6.28 m
高 6 cm 8 dm 10 m
侧面积
底面积
表面积
4 dm
1 m
6 cm
2 m
18.84 cm
25.12 dm
113.04 cm2
200.96 dm2
62.8 m2
28.26 cm2
50.24 dm2
3.14 m2
169.56 cm2
301.44 dm2
69.08 m2
(2) 王师傅要加工一根长2米,管口直径为2分米的圆柱形铁皮烟囱,至少需要铁皮( )平方米。
(3) 将直径是2厘米,高是5厘米的圆柱沿底面直径切成两个半圆柱后,表面积增加( )平方厘米。
1.256
20
2. 选择。
(1) 如果把圆柱的侧面沿高展开后得到一个正方形,那么圆柱的高等于( )。
① 底面直径 ② 底面直径的π倍 ③ 底面半径的π倍
(2) 圆柱的底面直径变成原来的2倍,高变成原来的,圆柱的侧面积( )。
① 是原来的2倍 ② 是原来的 ③ 不变
(3) 下面各图中,( )是圆柱的展开图。
① ② ③
(4) 如下图,将一个底面半径为 2分米、长1米的圆柱形木料截成 3个小圆柱后,
表面积增加( )平方分米。
① 4π ② 12π ③ 16π
②
③
②
③
3. 如下图,一辆压路机的滚筒是一个圆柱,它的长是2米,滚筒的横截面的直径是
1米。如果滚筒每分钟转5周,那么压路机每分钟能压路面多少平方米?
4. 王叔叔要做一对没有盖的圆柱形铁皮水桶,底面半径是2分米,高是10分米,做
这对水桶至少需要多少平方分米的铁皮?
5. 大厅内有8根同样的圆柱形支撑柱,每根高5米,底面周长是3.14米。如果每千克
油漆可漆2平方米,那么给这些支撑柱的表面刷油漆,需要油漆多少千克?
1×3.14×2×5=31.4(平方米)
(3.14×2×2×10+3.14×22)×2=276.32(平方分米)
3.14×5×8÷2=62.8(千克)
6. 把一个大圆柱截成两个小圆柱,两个小圆柱的高分别是4厘米和6厘米,它们的
表面积相差50.24平方厘米,原来大圆柱的表面积是多少?
50.24÷(6-4)=25.12(厘米)
(25.12÷3.14÷2)2×3.14×2+25.12×(4+6)=351.68(平方厘米) 解析:两个小圆柱的上、下底面面积相等,所以表面积差就是侧面积差,先用侧面积差÷高的差求出底面周长,再求表面积。
第4课时 圆柱的体积
1. 填空。
(1) 如右图,将一个圆柱切拼成一个长方体。长方体的底面积
等于圆柱的( ),长方体的高等于圆柱的( ),长方
体的体积等于( ),所以圆柱的体积也等于( )。
(2) 一个圆柱形钢坯的底面积是1.57平方分米,高是1米,体积是( )立
方分米。
(3) 一个圆柱形米桶,从里面量,底面周长是12.56分米,高是5分米,这个米
桶的容积是( )立方分米。
底面积
高
底面积×高
底面积×高
15.7
62.8
2. 判断。
(1) 一个圆柱和一个长方体的底面积和高都相等,圆柱的体积大一些。 ( )
(2) 表面积相等的两个圆柱,体积一定也相等。 ( )
(3) 把底面半径为4厘米,高为6厘米的圆柱切拼成体积相等的长方体,长方体
的表面积增加24平方厘米。 ( )
3. 计算下面各圆柱的体积。
(1) (2)
π×(6÷2)2×6=54π(dm3)
π×22×8=32π(cm3)
×
×
×
4. 一款圆柱形瓶装蜂蜜,小明从外面量,底面周长为 31.4厘米,高为12厘米。小
明认为蜂蜜量不实,生产商欺骗了消费者,他说的对吗?
5. 一个圆柱形蓄水池,底面直径是8米,高是2米,池内水深1.5米。这个圆柱形蓄
水池已蓄水多少立方米?
6. 李师傅将一个棱长为8分米的正方体削成一个最大的圆柱,圆柱的体积是多少?
(31.4÷3.14÷2)2×3.14×12=942(立方厘米)
942立方厘米=942毫升 942<950 对
(8÷2)2×3.14×1.5=75.36(立方米)
3.14×(8÷2)2×8=401.92(立方分米)
7. 把一个高5分米的圆柱的底面分成许多相等的扇形,然后把圆柱切开,再拼成一
个近似的长方体,表面积增加了40平方分米。圆柱的体积是多少立方分米?
40÷2÷5=4(分米) π×42×5=80π(立方分米)
解析:如图,表面积比原来增加的面积是左、右两个长方形的面积,长方形的一条边是圆柱的半径,与它相邻的另一条边是圆柱的高,增加的面积先除以2再除以高就可以求出圆柱的半径,再求体积即可。
第5课时 练 习 课(1)
1. 填空。
(1) 一个圆柱的底面半径是4分米,高是5分米,体积是( )立方分米。
(2) 强强家有一个底面积是15平方分米、高是6分米的圆柱形木质米桶,木材的
厚度不计,这个米桶的容积是( )立方分米,每升米重0.75千克,这个米桶
最多可装米( )千克。
(3) 挖一个底面周长是6.28米的圆柱形蓄水池,要使蓄水池能蓄水15.7立方米,
这个蓄水池要挖( )米深。
(4) 一个圆柱形玻璃水缸的底面周长是125.6厘米,水缸内有15厘米深的水,将
一块石头浸没在水中,水面上升到17厘米,这块石头的体积是( )立方厘
米。
80π
90
67.5
5
2512
2. 选择。
(1) 一个圆柱,高缩小为原来的,底面半径扩大为原来的2倍,体积( )。
① 不变 ② 扩大为原来的2倍 ③ 扩大为原来的4倍
(2) 一个长方体和一个圆柱的底面周长、高都相等,对比它们的体积,( )。
① 长方体的体积大 ② 圆柱的体积大
③ 长方体和圆柱的体积一样大
(3) 如下图,将底面直径为8厘米的圆柱切拼成长方体,表面积增加80平方厘米。
长方体的体积是( )立方厘米。
① 40π ② 160π
③ 320π
(4) 将一个高是 2 dm的圆柱按 2∶3 的体积比截成两个小圆柱后,表面积增加
50.24 cm2,截成后较小的小圆柱的体积是( )。
① 50.24cm3 ② 200.96cm3 ③ 301.44cm3
②
②
②
②
3. 一个自来水管的内直径是2厘米,管内的水流速度是每秒8厘米,如果一个自来水
管忘了关,5分钟会浪费多少升水?
4. 如下图,一个长方形长8分米,宽6分米。将它绕着边AB旋转一周,形成圆柱,该
圆柱的体积是多少立方分米?
5. 一个注满水的圆柱形容器的底面积是18平方分米,高是2分米,现将一个底面积
是10平方分米,高是2.5分米的圆柱形石柱垂直插入容器中,最多会有多少升水
溢出?
(2÷2)2×3.14×8×60×5=7536(立方厘米)=7.536升
π×6×6×8=288π(立方分米)
10×2=20(立方分米)=20升
6. 一个饮料瓶的瓶身如下图,饮料瓶的容积是3立方分米。它里面有一些饮料,正
放时饮料的高度为20厘米,倒放时空余部分的高度为5厘米。瓶内的饮料有多少
立方分米?
20∶5=4∶1
3÷(4+1)×4=2.4(立方分米)
解析:两个瓶中空余部分的体积相等,所以饮料的体积与空余部分的体积比为20∶5=4∶1,接着根据饮料瓶的容积和体积比求出饮料体积。
第6课时 练 习 课(2)
1. 填空。
(1) 一个圆柱的底面周长是94.2厘米,高是10厘米。它的表面积是( )平
方厘米,体积是( )立方厘米。
(2) 将棱长为4分米的正方体铁块熔铸成底面积是32平方分米的圆柱,圆柱的高
是( )分米。
(3) 填表。
2355
7065
2
圆 柱 底面 半径 底面 直径 底面积 高 表面积 体 积
2 cm 5 cm
10 dm 6 dm
4 cm
4π cm2
28π cm2
20π cm3
5 dm
25π dm2
110π dm2
150π dm3
2. 选择。
(1) 两个高相等的圆柱,底面的直径比是1∶3,则它们的体积比是( )。
① 1∶3 ② 1∶6 ③ 1∶9
(2) 乐乐有两张长18.84厘米、宽12.56厘米的长方形纸,他将它们分别卷成高
18.84厘米和12.56厘米的两个圆柱,这两个圆柱的体积相比,( )。
① 一样大 ② 高18.84厘米的体积大
③ 高12.56厘米的体积大
(3) 一个圆柱形水桶的容积是50升,底面积是20平方分米。若桶内盛水80%,则
水面距桶口( )分米。
① 0.5 ② 2 ③ 2.5
(4) 如下图,一张铁皮剪下图中阴影部分,正好可以做一个底面直径为4分米的
圆柱形油桶,这个油桶的容积是( )立方分米。
① 32π ② 64π ③ 16π2
③
③
①
①
3. 做一个底面半径是3分米,高是5分米的圆柱形无盖铁桶。
(1) 做这样一个铁桶至少需要多少平方分米的铁皮?
(2) 如果用这个铁桶盛水,那么最多能盛水多少升?
(3) 若将这些水倒入一个长6分米、宽5分米、高5分米的长方体水槽中,则水面
高多少分米?
4. 如下图,有一个长 2米、底面直径为0.8米的圆木,一半浮出水面,一半浸入水
中,圆木浸入水中的表面积、体积各是多少?
表面积:(0.8÷2)2×3.14+3.14×0.8×2÷2=3.0144(平方米)
体积:(0.8÷2)2×3.14×2÷2=0.5024(立方米)
3.14×3×2×5+3.14×32=122.46(平方分米)
3.14×32×5=141.3(立方分米) 141.3立方分米=141.3升
141.3÷(6×5)=4.71(分米)
5. 佳佳的生日蛋糕有两层,每层高0.5分米,底面直径分别是4分米、3分米。在这
个蛋糕的表面平均每平方分米抹40克奶油,制作这个蛋糕共需奶油多少克?
[4×3.14×0.5+3×3.14×0.5+(4÷2)2×
3.14]×40=942(克)
解析:蛋糕朝上的面合起来正好是一个圆,所以抹奶油的面积是直径分别为4分米、3分米,高为0.5分米的两个圆柱的侧面积加一个直径为4分米的圆的面积。
第7课时 圆锥的体积
1. 填空。
(1) 右图中的圆柱和圆锥等底等高,则圆柱的体积是圆锥的
( ),圆锥的体积是圆柱的( )。
(2) 一个圆锥和一个圆柱等底等高,若圆锥的体积是18立方分米,则圆柱的体
积是( )立方分米。若圆柱的体积是18立方分米,则圆锥的体积是( )立
方分米。
(3) 一个圆锥的底面直径是8米,高是3米。这个圆锥的占地面积是( )平
方米,体积是( )立方米。
(4) 一个圆锥的体积是20立方米,高是6米,它的底面积是( )平方米。
3倍
54
6
16π
16π
10
2. 判断。
(1) 圆柱的体积大于圆锥的体积。 ( )
(2) 圆锥的体积是和它等底等高的圆柱体积的。 ( )
(3) 一个圆柱比和它等底等高的圆锥体积大。 ( )
(4) 体积比是1∶3的圆锥和圆柱一定等底等高。 ( )
3. 计算圆锥的体积。
(1) (2)
×9×3.6=10.8(m3)
π×32×12×=36π(cm3)
√
×
×
×
4. 李阿姨有一个圆锥形斗笠,底面周长是12.56分米,高是3分米。这个斗笠的占
地面积是多少?体积是多少?
5. 小天把一个底面半径是1分米,高是3分米的圆锥形铝块放入一个有水的圆柱形
容器内(铝块完全浸没在水中,且水没溢出),容器内的水将上升多少立方分米?
6. 王师傅有一个圆锥形零件,底面积是36平方厘米,高是 9厘米。这个零件的体
积是多少立方厘米?如果将它熔铸成和它高相等的圆柱,那么圆柱的底面积是
多少?
12.56÷3.14÷2=2(分米) 占地面积:3.14×22=12.56(平方分米) 体积:12.56×3× =12.56(立方分米)
1×1×3.14×3÷3=3.14(立方分米)
体积:36×9÷3=108(立方厘米)
底面积:108÷9=12(平方厘米)
7. 将一个底面直径是2分米的圆锥形木料沿着高切成相等的两部分,表面积增加了
12平方分米。原来圆锥的体积是多少立方分米?
12÷2×2÷2=6(分米) (2÷2)2×3.14×6÷3=6.28(立方分米)
解析:表面积增加的是两个三角形的面积,三角形的底等于圆锥的直径,高等于圆锥的高。 增加的面积÷2=一个三角形的面积,一个三角形的面积×2÷直径=圆锥的高,然后求体积。
第8课时 练 习 课
1. 填空。
(1) 建筑工人使用的一种圆锥形铜锤,底面半径是3厘米,高是6厘米。每立方
厘米铜重8.9克,这个铜锤的体积是( )立方厘米,质量是( )克。
(2) 等底等高的圆柱和圆锥的体积相差300立方厘米,那么圆锥的体积是(
),圆柱的体积是( )。
(3) 一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积
是24立方分米,圆柱的体积是( )立方分米。
(4) 一辆货车的车厢是一个长方体,它的长是4米,宽是2.5米,高是2米,装满
一车厢沙子,卸下后的沙堆是一个高2米的圆锥。沙堆的底面积是( )。
56.52
503.028
150
立方厘米
450立方厘米
24
30平方米
2. 选择。
(1) 把一个圆柱形木料削成一个最大的圆锥,圆锥的体积是60立方厘米,削去
的体积是( )立方厘米。
① 20 ② 120 ③ 180
(2) 体积相等、高相等的圆锥和圆柱,圆锥的底面积是圆柱底面积的( )。
① ② 3倍 ③ 9倍
(3) 高和底面积相等的圆锥和长方体,圆锥体积是30 m3,长方体体积( )。
① 是60 m3 ② 是90 m3 ③ 大于90 m3
(4) 如下图,小陶在一个圆柱形容器里装满雪后,又压进一个与圆柱形容器等
底等高的圆锥形木块,压过后雪的体积是( )cm3。
① 64π ② 128π ③ 192π
②
②
②
②
3. 如下图,有一个直角三角形,如果将它绕着最长的直角边旋转可以得到一个圆
锥,这个圆锥的体积是多少?
4. 一个修路队把一堆底面半径是3米,高是1.5米的圆锥形砂石铺在10米宽的公路
上,若铺2厘米厚,能铺多少米长?
5. 如下图,一个粮仓由一个圆柱和一个圆锥组成。如果每立方米粮食约重200千克,
这个粮仓大约可盛粮食多少吨?
[(4÷2)2×3.14×2+(4÷2)2×3.14×1.5÷3]×200=6280(千克)=6.28吨
9×9×π×12÷3=324π(cm3)
2厘米=0.02米
32×3.14×1.5÷3÷(10×0.02)=70.65(米)
6. 一个圆柱和一个圆锥的底面积之比是1∶2,体积之比是5∶4。如果圆柱高30厘
米,那么圆锥高多少厘米?如果圆锥高30厘米,那么圆柱高多少厘米?
(5÷1)∶(4×3÷2)=5∶6
圆锥的高:30÷5×6=36(厘米)
圆柱的高:30÷6×5=25(厘米)
解析:可以先根据底面积和体积的比求出圆柱和圆锥高的比,再解答问题。
第9课时 整理与练习(1)
1. 填空。
(1) 一个圆柱的底面周长是6.28分米,高是3分米,这个圆柱的侧面积是( )
平方分米,表面积是( )平方分米。
(2) 一个圆柱的底面积是1.5平方分米,高是 6分米,和它等底等高的圆锥的体
积是( )立方分米。
(3) 做10节底面直径是8分米、高是10分米的圆柱形铁皮烟囱,需要铁皮( )
平方米。
(4) 有一个底面积是60平方分米、高是9分米的圆柱形钢坯,若熔铸成底面积是
60平方分米的圆锥形钢坯,则圆锥的高是( )分米;若熔铸成高是9分米的圆
锥形钢坯,则圆锥的底面积是( )平方分米。
18.84
25.12
3
25.12
27
180
2. 选择。
(1) 并排放的等底等高的圆锥和圆柱从不同方向看到的不同形状如图,从上面看
到的形状是( ),从左面看到的形状是( )。
① ② ③
(2) 下面的图以虚线为轴旋转,可以得到圆锥的是( )。
① ② ③
(3) 将圆柱的侧面沿一条直线剪开,不可能得到( )。
① 平行四边形 ② 长方形 ③ 梯形
(4) 底面积为6.28平方分米,高为3分米的圆柱内装有一半的水,现将一个和它
等底等高的圆锥放入其中,水面高( )。
① 正好是1.5分米 ② 正好是2.5分米 ③ 低于2.5分米,高于1.5分米
②
③
②
③
③
3. 妈妈的茶杯(如右图)放在桌上,底面直径是8厘米,高是15厘米。
(1) 这只茶杯占据桌面的面积是多少平方厘米?
(2) 茶杯中部有一圈隔热塑料,这圈隔热塑料宽3厘米,这圈隔热塑料的面积是
多少平方厘米
(3) 这只茶杯的容积是多少立方厘米?(茶杯厚度忽略不计)
4. 王叔叔加工了一个零件(如下图),你能计算出它的体积吗?
π×(2÷2)2×3÷3+π×(2÷2)2×
4=5π(dm3)
3.14×(8÷2)2=50.24(平方厘米)
3.14×8×3=75.36(平方厘米)
50.24×15=753.6(立方厘米)
5. 如图所示的长方体盒子里有一个圆柱,这个圆柱的体积最大是多少立方分米?
(结果保留π)
(6÷2)2 ×π×4=36π(dm3)
(4÷2)2 ×π×6=24π(dm3)
(4÷2)2 ×π×8=32π(dm3)
24π<32π<36π 最大是36π dm3
解析:圆柱有三种摆放情况,可以先画出三种底面,再想高,分别是d=6 dm,h=4 dm;d=4 dm,h=6 dm;d=4 dm,h=8 dm,然后依次求体积,最后选最大的。
第10课时 整理与练习(2)
1. 填空。
(1) 一个直角三角形的两条直角边分别长 6厘米和8厘米。将它绕一条直角边旋
转,所得圆锥的体积是( )立方厘米或( )立方厘米。
(2) 将底面周长是6.28分米的圆柱的高增加4分米,表面积增加(
),体积增加( )。
(3) 将一个圆柱沿直径切开,得到边长是8厘米的正方形切面,原来圆柱的表面
积是( )平方厘米,体积是( )立方厘米。
96π
128π
25.12平方分
米
12.56立方分米
96π
128π
2. 判断。
(1) 一个长方体和一个圆锥的体积相等,底面积也相等,则圆锥的高是长方体
高的3倍。 ( )
(2) 底面周长和高都相等的圆柱和长方体,圆柱的体积比长方体大。 ( )
(3) 将一个直径4厘米、高5厘米的圆柱切拼成和它等底等高的长方体,体积不
变,表面积增加20平方厘米。 ( )
(4) 等底等高的圆柱体积比圆锥大200%。 ( )
3. 李大爷要挖一口深15米,底面半径是4分米的水井。
(1) 挖这口水井,需挖土多少立方米?
(2) 水井外有一堆底面周长是3.14米,高0.6米的圆锥形砂石,将这堆砂石填入
井底,能铺多厚?(得数保留一位小数)
4分米=0.4米 0.42×3.14×15=7.536(立方米)
(3.14÷3.14÷2)2×3.14×0.6÷3÷(0.42×3.14)≈0.3(米)
√
√
√
√
4. 制作一个无盖的圆柱形水桶,有下图①②③④四种型号的铁皮可供选择。应选
择哪几号?所制作的水桶的表面积和容积各是多少?(铁皮厚度忽略不计)
5. 一听苹果汁的底面直径是6厘米,高是10厘米,现做一个纸箱来包装。(如下图)
(1) 做这个纸箱至少需要多少平方厘米的硬纸板?(箱盖折出的边缘和接头处忽
略不计)
(2) 这个长方体纸箱的体积是多少?
选择②号和③号
表面积:12.56×3+3.14×22=50.24(dm2)
容积:3.14×22×3=37.68(dm3)
长:6×6=36(厘米) 宽:4×6=24(厘米)
(36×24+36×10+24×10)×2=2928(平方厘米)
36×24×10=8640(立方厘米)
6. 王师傅将一根圆柱形木料削去一块后,变成下图的形状。你能求出它现在的体
积是多少吗?
π×(6÷2)2=9π(平方分米)
(13+7)×9π÷2=90π(立方分米)
解析:如图,解答此题时可以采用转化法,再增加一个一样的图形,使它变成一个规则的圆柱,求出体积后再除以2。
满分:100分 时间:60分钟 得分:_____
第二单元自主检测
一、填空。(每空1分,共24分)
1. 0.73立方米=( )立方分米 280毫升=( )升
2. 一个圆柱的底面半径是8厘米,高是20厘米,它的侧面积是( )平方厘米,
表面积是( )平方厘米,体积是( )立方厘米。
3. 一个圆锥的底面直径是6分米,高是底面直径的2倍,它的高是( )分米,底
面积是( )平方分米,体积是( )立方分米。
4. 一个圆柱和一个圆锥等底等高,如果圆柱的体积是 48立方米,那么圆锥的体积
是( )立方米;如果圆锥的体积比圆柱少 2.4立方分米,那么圆柱的体积是
( )立方分米。
730
0.28
320π
448π
1280π
12
9π
36π
16
3.6
5. 在一个棱长为4分米的正方体容器中装满水,再将水全部倒入一个高是8分米的圆
锥体容器中,正好倒满,圆锥的底面积是( )平方分米。
6. 圆柱的高不变,底面半径扩大为原来的3倍,侧面积扩大为原来的( )倍,体积
扩大为原来的( )倍。
7. 一个圆柱的底面直径是2分米,高是5分米,如果沿着底面直径分成两个同样的半
圆柱,表面积增加( )平方分米,如果分成3个同样的小圆柱,表面积增加
( )平方分米。
8. 如图,把圆柱切拼成一个近似的长方体。
(1) 长方体的前、后两个面的面积之和就是圆柱的( )。
(2) 如果圆柱的侧面积是62.8平方厘米,底面半径是2厘米,那么这个圆柱的体
积是( )立方厘米。
24
3
9
20
4π
侧面积
62.8
9. 一个圆柱高10厘米,若把它的高截短了3厘米,则表面积就减少了942平方厘米,
这个圆柱的底面积是( )平方分米,体积是( )立方分米。
10. 将一个底面边长是4分米,高是5分米的长方体木料加工成一个最大的圆柱,圆
柱的体积是( )立方分米。
11. 一个蔬菜大棚如下图,这个蔬菜大棚占地( )m2,覆盖大棚的塑料薄膜的
面积是( )m2,整个大棚内的空间是( )m3。
12. 一个圆柱和一个圆锥的底面半径的比是3∶4,高的比是2∶3,圆柱与圆锥的体
积比是( )。
78.5
78.5
20π
100
176.625
196.25
9∶8
二、判断。(每题1分,共5分)
1. 圆柱和圆锥的高都有无数条。 ( )
2. 圆锥的侧面展开图是一个三角形。 ( )
3. 底面积相等的圆锥和圆柱的体积比是1∶3。 ( )
4. 如果一个圆柱和长方体的底面周长和高都相等,那么长方体的表面积比圆柱的表
面积小。 ( )
5. 底面半径为r分米,高为h分米的圆柱的表面积是2πr(h+r)平方分米。 ( )
三、选择。(每题1分,共5分)
1. 求一个圆柱形水桶能装多少升水,就是求这个水桶的( )。
① 侧面积 ② 表面积 ③ 体积 ④ 容积
2. 如果一个圆柱的侧面展开图正好是一个正方形,那么这个圆柱的高和它底面直径
的比是( )。
① 1∶1 ② 1∶π ③ π∶1 ④ 1∶πd
×
×
√
√
×
④
③
3. 一张长12.56分米、宽3.14分米的长方形铁皮不能和( )分米的圆配成圆柱。
① 半径为0.5 ② 直径为1
③ 直径为4 ④ 周长为9.42
4. 将一个长方形绕下面不同的虚线旋转,旋转后体积最大的是( )。
① ② ③ ④
5. 如下图,将棱长相等的两块正方体木料A、B分别加工成1个和4个圆柱,剩下的木
料体积相比,( )。
① A大 ② B大
③ 一样大 ④ 无法确定
④
③
④
四、细心观察,正确操作。(每题3分,共6分)
1. 在方格纸上画出下面无盖圆柱体的表面展开图。
2. 在已有的底面的基础上画出高1厘米的圆锥。
五、看图列式计算。(共17分)
1. 计算下面各图形的表面积。(单位:厘米)(6分)
(1) (2)
2. 计算下面各图形的体积。(单位:厘米)(6分)
(1) (2)
3. 如下图,一个直角三角形以虚线为轴旋转一周,得到一个圆锥,它的体积是多少
立方厘米?(5分)
π×42×2+π×4×2×
5=72π(平方厘米)
π×(2÷2)2×2+π×2×
10=22π(平方厘米)
π×22×6×=8π(立方厘米)
π×(6÷2)2×9=81π(立方厘米)
π×32×4× =12π(立方厘米)
六、解决问题。(共43分)
1. 用塑料绳捆扎一个圆柱形蛋糕盒(如下图),打结处正好是底面圆心,打结用去塑
料绳25厘米。
(1) 捆扎这个蛋糕盒至少要用去塑料绳多少厘米?(3分)
(2) 在它的整个侧面贴上一圈商标纸,商标纸的面积至少是多少平方厘米?(3分)
(3) 这个蛋糕盒所占的空间是多少立方分米?(3分)
2. 砌一个圆柱形污水处理池,底面周长是18.84米,深3米。在处理池的周围和底面
抹上水泥。
(1) 抹水泥的面积是多少平方米?(4分)
(2) 这个污水处理池最多可以容纳污水多少立方米?(4分)
4×50+4×15+25=285(厘米)
50×3.14×15=2355(平方厘米)
(50÷2)2×3.14×15=29437.5(立方厘米)=29.4375立方分米
18.84×3+(18.84÷3.14÷2)2×3.14=84.78(平方米)
(18.84÷3.14÷2)2×3.14×3=84.78(立方米)
3. 一个圆锥形沙堆的底面半径是2米,高是1.8米。每立方米沙约重1.5吨,这堆沙
约重多少吨?(5分)
4. 一个圆柱形水桶的容积是20立方分米,里面装了的水。已知水桶的底面积是6平
方分米,水面高多少分米?(5分)
5. 小明为了测量出一个土豆的体积,按如下步骤进行了一个实验:在一个底面直径
是8厘米的圆柱形玻璃杯中装入一定量的水,量得水面的高度是5厘米;将土豆放
入水中,再次量得水面的高度是7厘米。如果玻璃的厚度忽略不计,那么这个土
豆的体积大约是多少立方厘米?(5分)
3.14×(8÷2)2×(7-5)=100.48(立方厘米)
×3.14×22×1.8×1.5=11.304(吨)
20×÷6= (分米)
6. 如图,一个沙漏由两个圆锥组成,每个圆锥底面半径是 6厘米,高是10厘米。沙
漏里的沙子正好可以填满一个圆锥。沙漏里沙子的体积是多少?如果每分钟漏掉
20立方厘米的沙子,沙漏里的沙子从一头漏到另一头要多少分钟?(6分)
7. 如下图,阴影部分的材料正好可以做成一个圆柱,求这个圆柱的体积。(5分)
3.14×62×10÷3=376.8(立方厘米) 376.8÷20=18.84(分钟)
12.56÷3.14÷2=2(分米)
2×4=8(分米)
3.14×22×8=100.48(立方分米)
