第三单元 图形的运动 -2022-2023学年六年级数学下册单元考点梳理与精炼(北师大版)(含答案)
文档属性
| 名称 | 第三单元 图形的运动 -2022-2023学年六年级数学下册单元考点梳理与精炼(北师大版)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 743.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 15:19:39 | ||
图片预览

文档简介
第三单元 图形的运动
1、旋转的意义。
在平面内,将一个图形绕一个定点O沿某个方向转动一定的角度,这样的图形运动称为旋转。
(1)经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了相同的角度,对应点的排列顺序相同。
(2)任意一对对应点与旋转中心的连线所成的角都是旋转角。
(3)对应点到旋转中心的距离相等。
(4)对应线段相等,对应角相等。
2、旋转画图的具体步骤。
(1)分析题目的要求,找出旋转中心和旋转角度;
(2)分析所画的图形,找出围成图形的关键点;
(3)沿一定的方向,按一定的角度,通过截取线段的方法,旋转各个关键点。
1.下面( )的运动是平移。
A.钟摆 B.拔算珠 C.电风扇
2.把绕点A逆时针旋转后得到的图形是( )。
A. B. C.
3.将下面的图案绕点“O”按顺时针方向旋转90°,得到的图案是( )。
A. B. C. D.
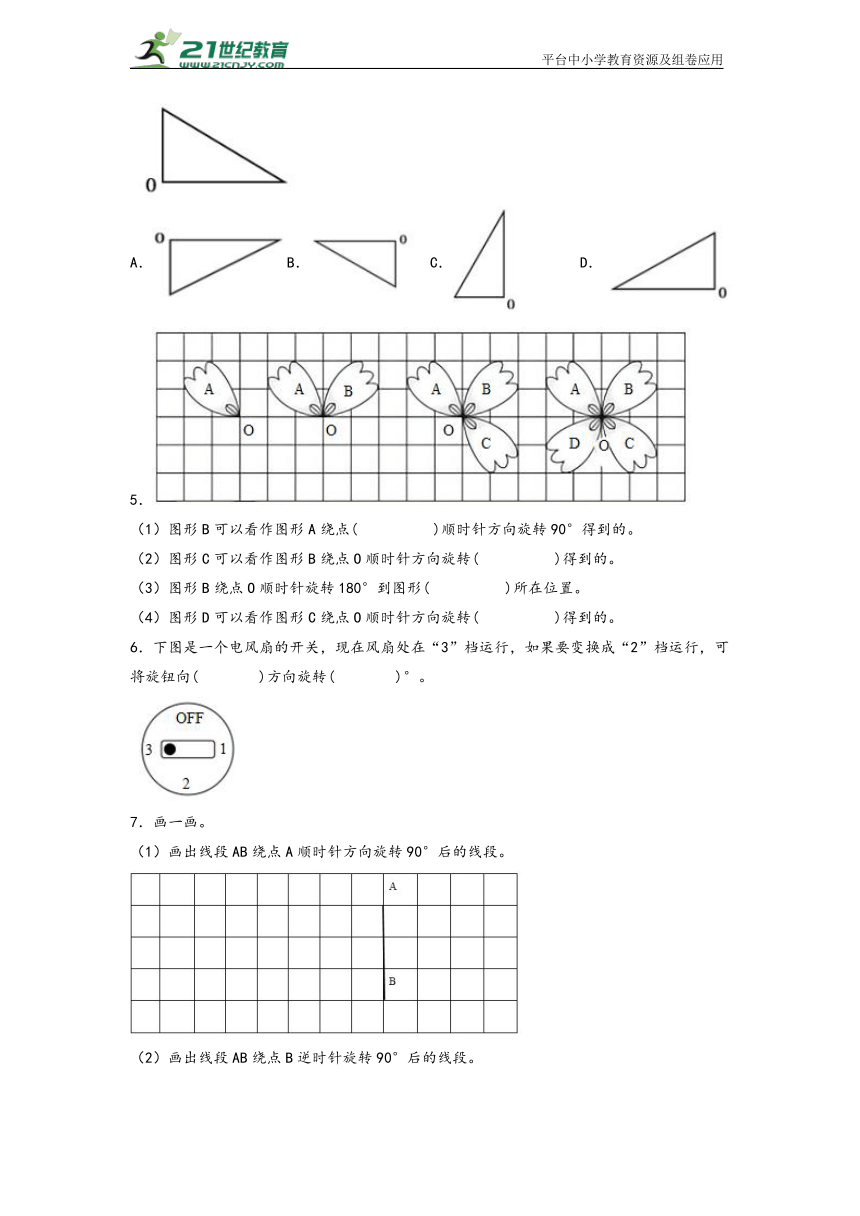
4.将下图直角三角形绕O点逆时针旋转90°可以得到图形( )。
A.B. C. D.
5.
(1)图形B可以看作图形A绕点( )顺时针方向旋转90°得到的。
(2)图形C可以看作图形B绕点O顺时针方向旋转( )得到的。
(3)图形B绕点O顺时针旋转180°到图形( )所在位置。
(4)图形D可以看作图形C绕点O顺时针方向旋转( )得到的。
6.下图是一个电风扇的开关,现在风扇处在“3”档运行,如果要变换成“2”档运行,可将旋钮向( )方向旋转( )°。
7.画一画。
(1)画出线段AB绕点A顺时针方向旋转90°后的线段。
(2)画出线段AB绕点B逆时针旋转90°后的线段。
8.用“旋转”描述栏杆的运动过程:
9.在五年级数学直播课上,刘老师让同学们按要求进行画图。
(1)把图1绕点O顺时针旋转90°,得到图2。
(2)把图1绕点O逆时针旋转90°,得到图3。
(3)把图2绕点O顺时针旋转90°,得到图4。
(4)把图1,图2,图3,图4都涂上红色。看到这个图形你想到了什么?
1、利用轴对称、平移、旋转等方法绘制精美的图案。
2、在单一图案花边的绘制过程中,基本图形的大小、方向、形状不会发生变化,基本图形平移的格数也是不变的。
3、设计步骤:确定要设计的图案、基本图形、变换方法;将要设计的图案在方格纸上画出来。
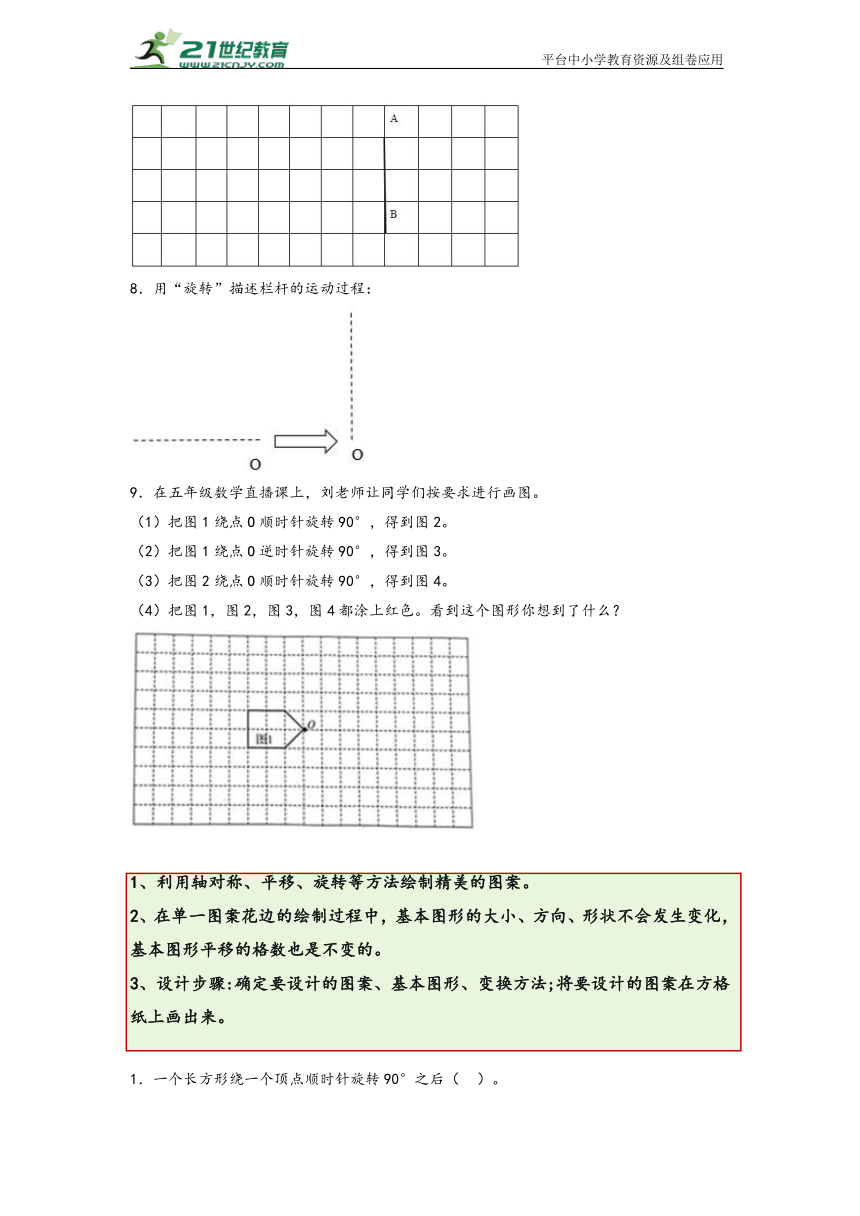
1.一个长方形绕一个顶点顺时针旋转90°之后( )。
A.形状改变 B.面积变大 C.周长变小 D.以上都错
2.如图,能够使图形A得到图形B的方法是( )。
A.先绕点O顺时针旋转90°,再向上平移1格 B.先绕点O逆时针旋转90°,再向下平移1格
C.先绕点O顺时针旋转90°,再向下平移1格 D.先绕点O逆时针旋转90°,再向上平移1格
3.图形A( )可以得到图形B。
A.先向右平移5格,再向上平移2格
B.先向右平移7格,再以直角顶点为中心逆时针旋转90°,然后向上平移1格
C.先以直角顶点为中心顺时针旋转90°,再向右平移5格
D.先向右平移5格,再以直角顶点为中心逆时针旋转90°
4.下列说法中不正确的是( )。
A.平移不改变图形的形状和大小
B.平移中,图形上每个点移动的距离可以不同
C.经过平移,图形的对应线段、对应角分别相等
D.经过平移,图形对应点的连结线段平行且相等
5.图形向( )平移( )格,再向( )平移( )格,就能与图形拼成一个完整图形了。
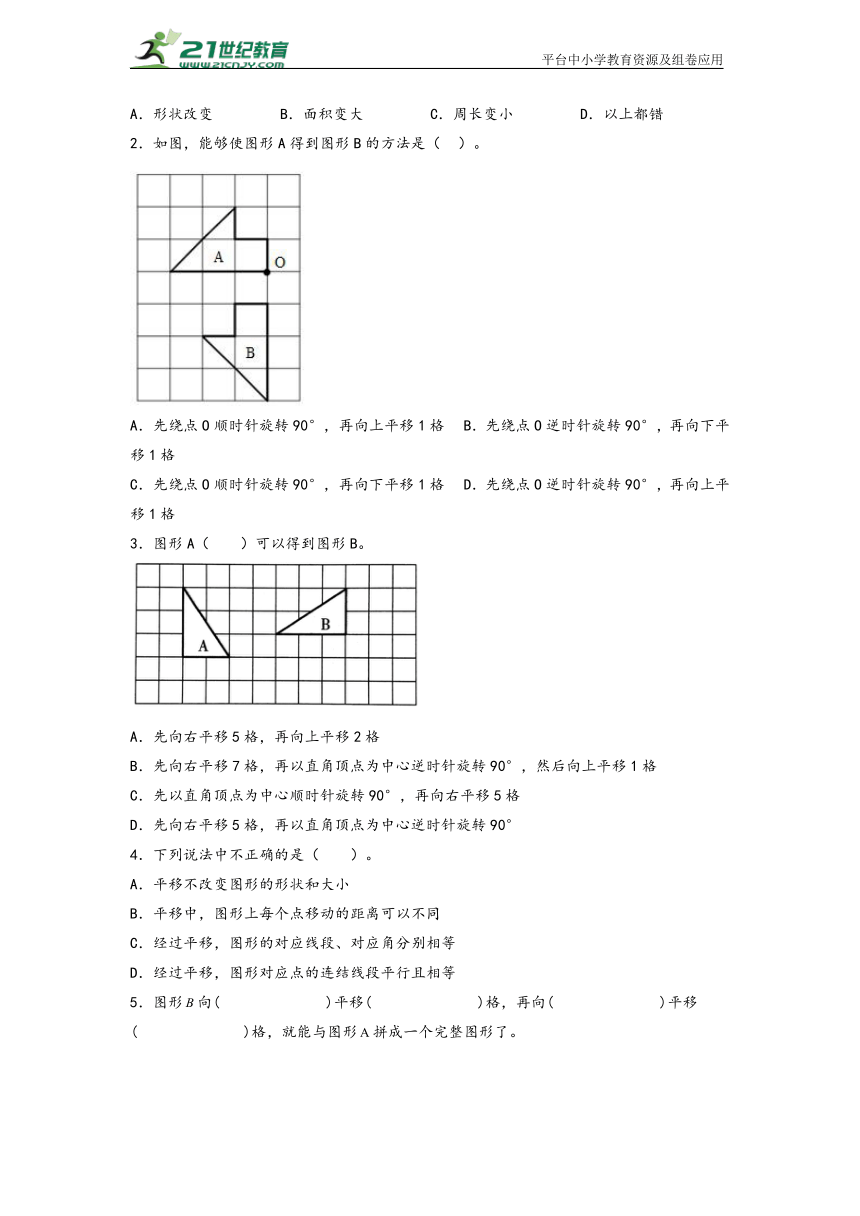
6.在生活中,我们利用_____、_____和_____能设计出许多美丽的图案。
7.
(1)图形A是如何运动得到图形B的?
(2)图形B是如何运动得到图形C的?
8.(1)图形①经过怎样的运动得到图形②,把经过写下来。
(2)画出图形③绕点O逆时针旋转90度后的图形。
9.张小明同学为班级“学习专栏”设计了报头图案,并用文字说明图案的含义,如图①请你用基本的几何图形(如直线、射线、线段、角、三角形、平行四边形、长方形、正方形等)中若干个为“环保专栏”在下图框中设计一个报头图案,并简要说明图案的含义。
参考答案
考点一
1.B
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向做相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变;旋转:在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】A.钟摆是旋转运动;
B.拔算珠是平移运动;
C.电风扇是旋转运动;
故答案为:B
【点睛】此题考查了平移和旋转的意义及在实际当中的运用。
2.C
【分析】在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转;这个定点叫旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。与时针转动方向相同的是顺时针旋转,反之就是逆时针旋转。据此选择。
【详解】由分析可知:
把绕点A逆时针旋转后得到的图形是。
故答案为:C
【点睛】本题考查了旋转的意义,应熟练掌握。
3.B
4.C
5. O 90° D 90°
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
【详解】(1)图形B可以看作图形A绕点O顺时针方向旋转90°得到的;
(2)图形C可以看作图形B绕点O顺时针方向旋转90°得到的;
(3)图形B绕点O顺时针旋转180°到图形D所在位置;
(4)图形D可以看作图形C绕点O顺时针方向旋转90°得到的。
【点睛】本题考查了旋转与旋转现象,物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。
6. 逆时针 90
【分析】2在3的右下方,由于顺时针转90°会到OFF处,即逆时针转90°会到“2”档处。
【详解】由分析可知:如果要变换成“2”档运行,可将旋钮向逆时针方向旋转90°。
【点睛】本题主要考查旋转方向和旋转角度,要注意和时针旋转方向相同为顺时针,和时针旋转方向相反为逆时针。
13.(1)
(2)
8.栏杆绕点O顺时针旋转90°
【分析】在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。这个点为旋转中心,旋转的角度叫旋转角。据此解答
【详解】答:栏杆绕点O顺时针旋转90°。
【点睛】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
9.(1)把图1绕点O顺时针旋转90°,得到图2(下图)。
(2)把图1绕点O逆时针旋转90°,得到图3(下图)。
(3)把图2绕点O顺时针旋转90°,得到图4(下图)。
(4)把图1,图2,图3,图4都涂上红色(下图)。看到这个图形“我”想到了医院的红“十”字。
考点二
1.D
【分析】把一个图形绕着某一点转动一个角度的图形变换叫做旋转,根据旋转的特征来对每个选项进行判断即可。
【详解】A.物体或图形旋转后,它们的形状不改变,所以该选项错误。
B.物体或图形旋转后,它们大小不改变,即面积不会改变,所以该选项错误。
C.物体或图形旋转后,它们的形状、大小都不改变,即周长不会改变,所以该选项错误
D.旋转的特征为:物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。
故答案为:D
【点睛】本题考查了对旋转特征的掌握和灵活运用。
2.B
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。
旋转:在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】能够使图形A得到图形B的方法是先绕点O逆时针旋转90°,再向下平移1格。
故答案为:B
【点睛】此题考查了平移与旋转的意义及在实际当中的运用。
3.B
4.B
5. 上 1 左 3
【分析】根据图形的平移方法进行分析并填空即可。
【详解】图形向上平移1格,再向左平移3格,就能与图形拼成一个完整图形了。
【点睛】熟练掌握物体的平移方法是解答此题的关键
6. 平移 旋转 轴对称
【详解】根据平移、旋转和轴对称等图形变换的方法,可以设计出许多美丽的图案。
7.(1)先向右平移8格,再顺时针旋转90°得到图形B;(2)图形B绕中心点顺时针旋转90°得到图形C。
8.(1)图形①先向右平移8个格,再绕中心点顺时针旋转90°得到图形②;
(2)见详解
【分析】(1)根据平移和旋转的特点,图形①先向右平移再通过旋转可以得到图形②,确定平移的距离和旋转方向和角度即可,答案不唯一。
(2)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点,顺次连接作出的各点即可。
【详解】(1)图形①先向右平移8个格,再绕中心点顺时针旋转90°得到图形②。
(2)
【点睛】决定平移后图形的位置的要素:一是平移的方向,二是平移的距离。决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
9.见详解
【分析】本题是开放型发散思维的题目,答案不唯一,合理即可。
【详解】
含义:请走近垃圾箱,将垃圾放入箱内。
【点睛】主要考查了平移,旋转,轴对称等变换的作图,要掌握它们的基本性质才能灵活运用并设计出合理的图案。
平台中小学教育资源及组卷应用
1、旋转的意义。
在平面内,将一个图形绕一个定点O沿某个方向转动一定的角度,这样的图形运动称为旋转。
(1)经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了相同的角度,对应点的排列顺序相同。
(2)任意一对对应点与旋转中心的连线所成的角都是旋转角。
(3)对应点到旋转中心的距离相等。
(4)对应线段相等,对应角相等。
2、旋转画图的具体步骤。
(1)分析题目的要求,找出旋转中心和旋转角度;
(2)分析所画的图形,找出围成图形的关键点;
(3)沿一定的方向,按一定的角度,通过截取线段的方法,旋转各个关键点。
1.下面( )的运动是平移。
A.钟摆 B.拔算珠 C.电风扇
2.把绕点A逆时针旋转后得到的图形是( )。
A. B. C.
3.将下面的图案绕点“O”按顺时针方向旋转90°,得到的图案是( )。
A. B. C. D.
4.将下图直角三角形绕O点逆时针旋转90°可以得到图形( )。
A.B. C. D.
5.
(1)图形B可以看作图形A绕点( )顺时针方向旋转90°得到的。
(2)图形C可以看作图形B绕点O顺时针方向旋转( )得到的。
(3)图形B绕点O顺时针旋转180°到图形( )所在位置。
(4)图形D可以看作图形C绕点O顺时针方向旋转( )得到的。
6.下图是一个电风扇的开关,现在风扇处在“3”档运行,如果要变换成“2”档运行,可将旋钮向( )方向旋转( )°。
7.画一画。
(1)画出线段AB绕点A顺时针方向旋转90°后的线段。
(2)画出线段AB绕点B逆时针旋转90°后的线段。
8.用“旋转”描述栏杆的运动过程:
9.在五年级数学直播课上,刘老师让同学们按要求进行画图。
(1)把图1绕点O顺时针旋转90°,得到图2。
(2)把图1绕点O逆时针旋转90°,得到图3。
(3)把图2绕点O顺时针旋转90°,得到图4。
(4)把图1,图2,图3,图4都涂上红色。看到这个图形你想到了什么?
1、利用轴对称、平移、旋转等方法绘制精美的图案。
2、在单一图案花边的绘制过程中,基本图形的大小、方向、形状不会发生变化,基本图形平移的格数也是不变的。
3、设计步骤:确定要设计的图案、基本图形、变换方法;将要设计的图案在方格纸上画出来。
1.一个长方形绕一个顶点顺时针旋转90°之后( )。
A.形状改变 B.面积变大 C.周长变小 D.以上都错
2.如图,能够使图形A得到图形B的方法是( )。
A.先绕点O顺时针旋转90°,再向上平移1格 B.先绕点O逆时针旋转90°,再向下平移1格
C.先绕点O顺时针旋转90°,再向下平移1格 D.先绕点O逆时针旋转90°,再向上平移1格
3.图形A( )可以得到图形B。
A.先向右平移5格,再向上平移2格
B.先向右平移7格,再以直角顶点为中心逆时针旋转90°,然后向上平移1格
C.先以直角顶点为中心顺时针旋转90°,再向右平移5格
D.先向右平移5格,再以直角顶点为中心逆时针旋转90°
4.下列说法中不正确的是( )。
A.平移不改变图形的形状和大小
B.平移中,图形上每个点移动的距离可以不同
C.经过平移,图形的对应线段、对应角分别相等
D.经过平移,图形对应点的连结线段平行且相等
5.图形向( )平移( )格,再向( )平移( )格,就能与图形拼成一个完整图形了。
6.在生活中,我们利用_____、_____和_____能设计出许多美丽的图案。
7.
(1)图形A是如何运动得到图形B的?
(2)图形B是如何运动得到图形C的?
8.(1)图形①经过怎样的运动得到图形②,把经过写下来。
(2)画出图形③绕点O逆时针旋转90度后的图形。
9.张小明同学为班级“学习专栏”设计了报头图案,并用文字说明图案的含义,如图①请你用基本的几何图形(如直线、射线、线段、角、三角形、平行四边形、长方形、正方形等)中若干个为“环保专栏”在下图框中设计一个报头图案,并简要说明图案的含义。
参考答案
考点一
1.B
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向做相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变;旋转:在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】A.钟摆是旋转运动;
B.拔算珠是平移运动;
C.电风扇是旋转运动;
故答案为:B
【点睛】此题考查了平移和旋转的意义及在实际当中的运用。
2.C
【分析】在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转;这个定点叫旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。与时针转动方向相同的是顺时针旋转,反之就是逆时针旋转。据此选择。
【详解】由分析可知:
把绕点A逆时针旋转后得到的图形是。
故答案为:C
【点睛】本题考查了旋转的意义,应熟练掌握。
3.B
4.C
5. O 90° D 90°
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
【详解】(1)图形B可以看作图形A绕点O顺时针方向旋转90°得到的;
(2)图形C可以看作图形B绕点O顺时针方向旋转90°得到的;
(3)图形B绕点O顺时针旋转180°到图形D所在位置;
(4)图形D可以看作图形C绕点O顺时针方向旋转90°得到的。
【点睛】本题考查了旋转与旋转现象,物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。
6. 逆时针 90
【分析】2在3的右下方,由于顺时针转90°会到OFF处,即逆时针转90°会到“2”档处。
【详解】由分析可知:如果要变换成“2”档运行,可将旋钮向逆时针方向旋转90°。
【点睛】本题主要考查旋转方向和旋转角度,要注意和时针旋转方向相同为顺时针,和时针旋转方向相反为逆时针。
13.(1)
(2)
8.栏杆绕点O顺时针旋转90°
【分析】在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。这个点为旋转中心,旋转的角度叫旋转角。据此解答
【详解】答:栏杆绕点O顺时针旋转90°。
【点睛】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
9.(1)把图1绕点O顺时针旋转90°,得到图2(下图)。
(2)把图1绕点O逆时针旋转90°,得到图3(下图)。
(3)把图2绕点O顺时针旋转90°,得到图4(下图)。
(4)把图1,图2,图3,图4都涂上红色(下图)。看到这个图形“我”想到了医院的红“十”字。
考点二
1.D
【分析】把一个图形绕着某一点转动一个角度的图形变换叫做旋转,根据旋转的特征来对每个选项进行判断即可。
【详解】A.物体或图形旋转后,它们的形状不改变,所以该选项错误。
B.物体或图形旋转后,它们大小不改变,即面积不会改变,所以该选项错误。
C.物体或图形旋转后,它们的形状、大小都不改变,即周长不会改变,所以该选项错误
D.旋转的特征为:物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。
故答案为:D
【点睛】本题考查了对旋转特征的掌握和灵活运用。
2.B
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。
旋转:在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】能够使图形A得到图形B的方法是先绕点O逆时针旋转90°,再向下平移1格。
故答案为:B
【点睛】此题考查了平移与旋转的意义及在实际当中的运用。
3.B
4.B
5. 上 1 左 3
【分析】根据图形的平移方法进行分析并填空即可。
【详解】图形向上平移1格,再向左平移3格,就能与图形拼成一个完整图形了。
【点睛】熟练掌握物体的平移方法是解答此题的关键
6. 平移 旋转 轴对称
【详解】根据平移、旋转和轴对称等图形变换的方法,可以设计出许多美丽的图案。
7.(1)先向右平移8格,再顺时针旋转90°得到图形B;(2)图形B绕中心点顺时针旋转90°得到图形C。
8.(1)图形①先向右平移8个格,再绕中心点顺时针旋转90°得到图形②;
(2)见详解
【分析】(1)根据平移和旋转的特点,图形①先向右平移再通过旋转可以得到图形②,确定平移的距离和旋转方向和角度即可,答案不唯一。
(2)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点,顺次连接作出的各点即可。
【详解】(1)图形①先向右平移8个格,再绕中心点顺时针旋转90°得到图形②。
(2)
【点睛】决定平移后图形的位置的要素:一是平移的方向,二是平移的距离。决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
9.见详解
【分析】本题是开放型发散思维的题目,答案不唯一,合理即可。
【详解】
含义:请走近垃圾箱,将垃圾放入箱内。
【点睛】主要考查了平移,旋转,轴对称等变换的作图,要掌握它们的基本性质才能灵活运用并设计出合理的图案。
平台中小学教育资源及组卷应用
