2.2.3直线的一般式方程课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(共31张PPT)
文档属性
| 名称 | 2.2.3直线的一般式方程课件-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 08:04:04 | ||
图片预览










文档简介
(共31张PPT)
2.2.3 直线的一般式方程
第二章
2.2
直线的方程
名 称 方程
点斜式
斜截式
两点式
截距式
条 件
适用范围
新知学习
链接回顾
新知讲解
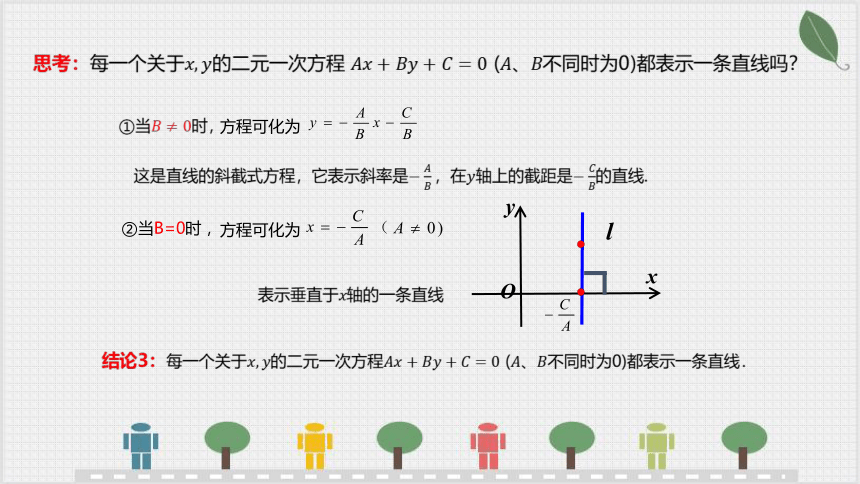
②当B=0时,
l
x
y
O
方程可化为
方程可化为
我们把关于x,y的二元一次方程
(其中A、B不同时为0)
直线的一般式方程:
叫做直线的一般式方程,简称一般式.
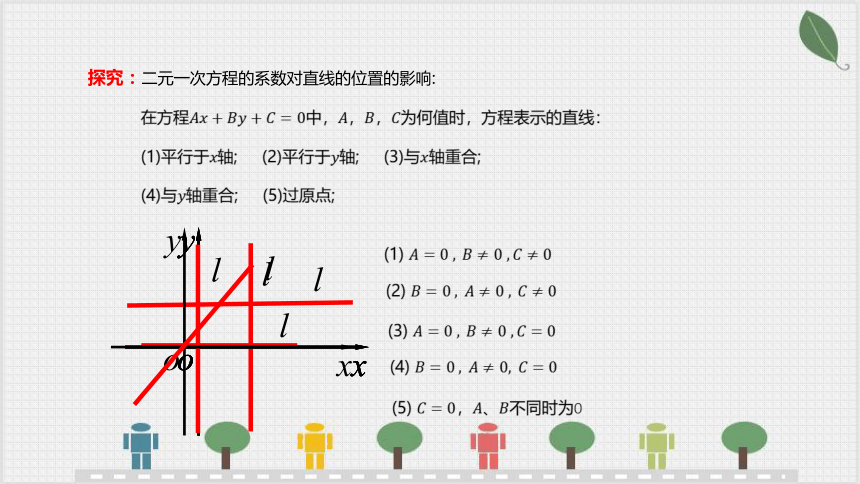
探究:二元一次方程的系数对直线的位置的影响:
解:
典例剖析
设直线l的方程为(m2-2m-3)x-(2m2+m-1)y+6-2m=0.
(1)已知直线l在x轴上的截距为-3,求m的值;
解 由题意知m2-2m-3≠0,即m≠3且m≠-1,
典例
设直线l的方程为(m2-2m-3)x-(2m2+m-1)y+6-2m=0.
(2)已知直线l的斜率为1,求m的值.
由直线l化为斜截式方程
得m=-2或m=-1(舍去).
∴m=-2.
延伸探究
设直线l的方程为(m2-2m-3)x-(2m2+m-1)y+6-2m=0.
对于本例中的直线l的方程,若直线l与y轴平行,求m的值.
解 ∵直线l与y轴平行,
例2 直线
试讨论:(1) 的条件是什么?
(2) 的条件是什么?
方法二
方法一
两条直线位置关系的判断
例2. (1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
法二:令2×3=m(m+1),解得m=-3或m=2.
当m=-3时,l1:x-y+2=0,l2:3x-3y+2=0,显然l1与l2不重合,∴l1∥l2.
同理当m=2时,l1:2x+3y+4=0,l2:2x+3y-2=0,
l1与l2不重合,l1∥l2,∴m的值为2或-3.
法二:由直线l1⊥l2,
所以(a+2)(a-1)+(1-a)(2a+3)=0,解得a=±1.
将a=±1代入方程,均满足题意.故当a=1或a=-1时,直线l1⊥l2.
(2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0互相垂直?
跟踪训练
直线系方程
直线系方程
解:(1) 设所求直线的方程为
解得:
所以所求直线的方程为
(2) 设所求直线的方程为
解得:
所以所求直线的方程为
求满足下列条件的直线的方程
跟踪训练
D
D
巩固训练
4.过点P(1,4)作直线与两坐标轴正半轴相交,当直线在两坐标轴上
的截距之和最小时,求此直线的方程.
当且仅当
即
即
解1:
x
y
O
P(1,4)
4.过点P(1,4)作直线与两坐标轴正半轴相交,当直线在两坐标轴上
的截距之和最小时,求此直线的方程.
解2:
x
y
O
P(1,4)
优化设计小本
点斜式
斜截式
两点式
点斜式
截距式
化成一般式
1.直线方程的形式
课堂小结
2.直线位置关系的判断
3.直线系方程
谢 谢!
2.2.3 直线的一般式方程
第二章
2.2
直线的方程
名 称 方程
点斜式
斜截式
两点式
截距式
条 件
适用范围
新知学习
链接回顾
新知讲解
②当B=0时,
l
x
y
O
方程可化为
方程可化为
我们把关于x,y的二元一次方程
(其中A、B不同时为0)
直线的一般式方程:
叫做直线的一般式方程,简称一般式.
探究:二元一次方程的系数对直线的位置的影响:
解:
典例剖析
设直线l的方程为(m2-2m-3)x-(2m2+m-1)y+6-2m=0.
(1)已知直线l在x轴上的截距为-3,求m的值;
解 由题意知m2-2m-3≠0,即m≠3且m≠-1,
典例
设直线l的方程为(m2-2m-3)x-(2m2+m-1)y+6-2m=0.
(2)已知直线l的斜率为1,求m的值.
由直线l化为斜截式方程
得m=-2或m=-1(舍去).
∴m=-2.
延伸探究
设直线l的方程为(m2-2m-3)x-(2m2+m-1)y+6-2m=0.
对于本例中的直线l的方程,若直线l与y轴平行,求m的值.
解 ∵直线l与y轴平行,
例2 直线
试讨论:(1) 的条件是什么?
(2) 的条件是什么?
方法二
方法一
两条直线位置关系的判断
例2. (1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
法二:令2×3=m(m+1),解得m=-3或m=2.
当m=-3时,l1:x-y+2=0,l2:3x-3y+2=0,显然l1与l2不重合,∴l1∥l2.
同理当m=2时,l1:2x+3y+4=0,l2:2x+3y-2=0,
l1与l2不重合,l1∥l2,∴m的值为2或-3.
法二:由直线l1⊥l2,
所以(a+2)(a-1)+(1-a)(2a+3)=0,解得a=±1.
将a=±1代入方程,均满足题意.故当a=1或a=-1时,直线l1⊥l2.
(2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0互相垂直?
跟踪训练
直线系方程
直线系方程
解:(1) 设所求直线的方程为
解得:
所以所求直线的方程为
(2) 设所求直线的方程为
解得:
所以所求直线的方程为
求满足下列条件的直线的方程
跟踪训练
D
D
巩固训练
4.过点P(1,4)作直线与两坐标轴正半轴相交,当直线在两坐标轴上
的截距之和最小时,求此直线的方程.
当且仅当
即
即
解1:
x
y
O
P(1,4)
4.过点P(1,4)作直线与两坐标轴正半轴相交,当直线在两坐标轴上
的截距之和最小时,求此直线的方程.
解2:
x
y
O
P(1,4)
优化设计小本
点斜式
斜截式
两点式
点斜式
截距式
化成一般式
1.直线方程的形式
课堂小结
2.直线位置关系的判断
3.直线系方程
谢 谢!
