3.3.2 抛物线的简单几何性质 课件(共69张PPT)
文档属性
| 名称 | 3.3.2 抛物线的简单几何性质 课件(共69张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 00:00:00 | ||
图片预览






文档简介
(共69张PPT)
第 3 章圆锥曲线的方程
人教A版2019选修第一册
3.3.2 抛物线的简单几何性质
其中定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线
定义告诉我们:
(1)判断抛物线的一种方法
(2)抛物线上任一点的性质:|MF|=d
1.抛物线的定义
平面内与一个定点F 和一条定直线l (l 不经过点F)的距离相等的点的轨迹叫做抛物线.
┑
l
F
M
d
H
知识回顾
图形 标准方程 焦点坐标 准线方程 焦点位置
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
2.四种抛物线及其标准方程
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
由抛物线 y2 =2px(p>0)
有
所以抛物线的范围为
如何研究抛物线y2 =2px(p>0)的几何性质
1.范围
x
l
F
y
O
新知探究
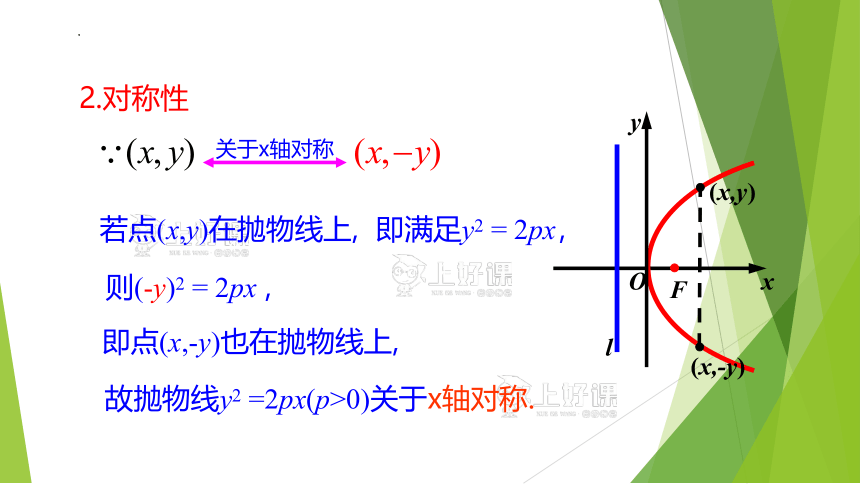
关于x轴对称
即点(x,-y)也在抛物线上,
故抛物线y2 =2px(p>0)关于x轴对称.
则(-y)2 = 2px ,
若点(x,y)在抛物线上, 即满足y2 = 2px,
2.对称性
x
l
F
(x,y)
y
O
(x,-y)
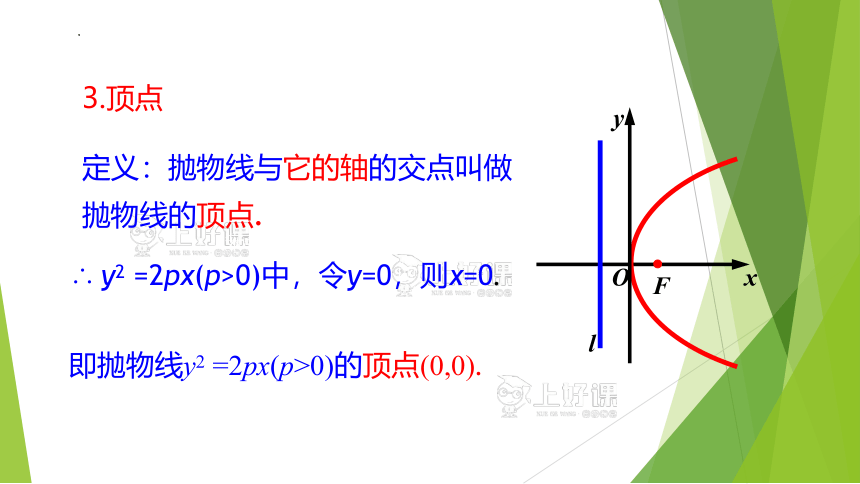
定义:抛物线与它的轴的交点叫做抛物线的顶点.
∴ y2 =2px(p>0)中,令y=0,则x=0.
即抛物线y2 =2px(p>0)的顶点(0,0).
3.顶点
x
l
F
y
O
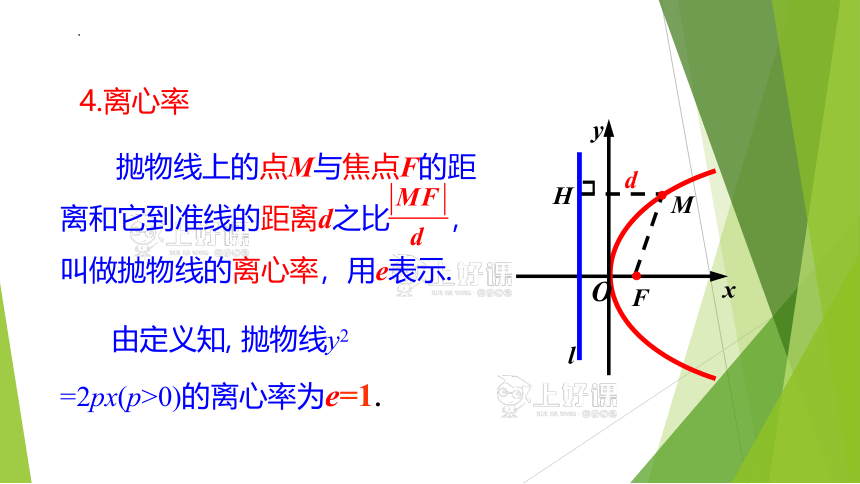
由定义知, 抛物线y2 =2px(p>0)的离心率为e=1.
4.离心率
x
┑
l
F
M
d
H
y
O
抛物线上的点M与焦点F的距离和它到准线的距离d之比 ,叫做抛物线的离心率,用e表示.
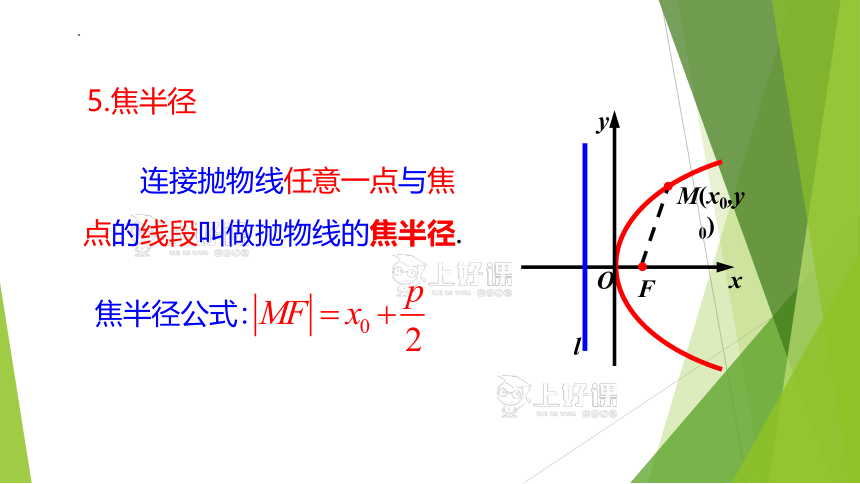
连接抛物线任意一点与焦点的线段叫做抛物线的焦半径.
焦半径公式:
5.焦半径
x
l
F
M
y
O
(x0,y0)
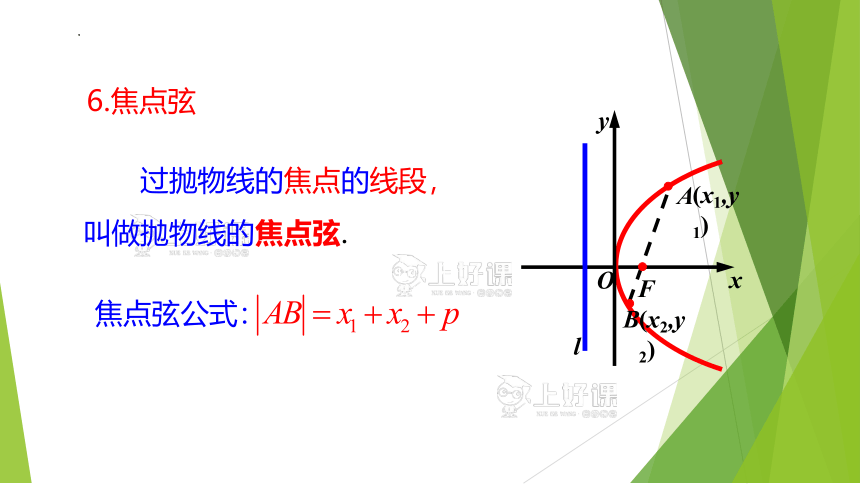
过抛物线的焦点的线段,叫做抛物线的焦点弦.
焦点弦公式:
6.焦点弦
x
l
F
A
y
O
B
(x1,y1)
(x2,y2)
A
B
y2=2px
2p
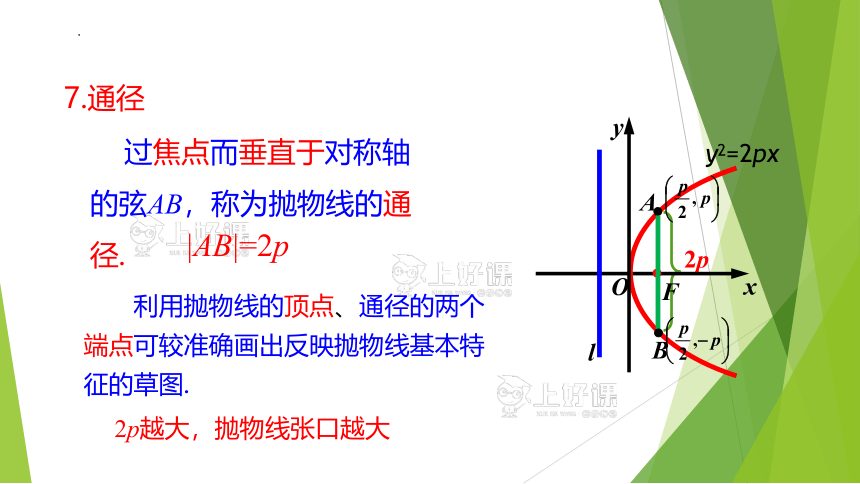
过焦点而垂直于对称轴的弦AB,称为抛物线的通径.
|AB|=2p
2p越大,抛物线张口越大
7.通径
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
x
l
F
y
O
方程
图形
范围
对称性
顶点
焦半径
焦点弦
通径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0, y∈R
x≤0, y∈R
x∈R, y≥0
x∈R, y≤0
l
F
y
x
O
关于x轴对称
关于y轴对称
(0,0)
抛物线的简单几何性质
如图,已知线段AB是抛物线y2=2px(p>0)的焦点弦,且A(x1,y1),B(x2,y2),点F是抛物线的焦点,过A,B两点分别作准线l的垂线AC,BD,垂足分别为点C,D,点M为线段AB的中点,点M′为线段CD的中点.
【方法技巧与总结】
点P(x0,y0)与抛物线y2=2px(p>0)的关系
(1)P在抛物线内(含焦点).
(2)P在抛物线上.
(3)P在抛物线外.
p的几何意义
p为焦点到准线l的距离,即焦准距,
p越大,抛物线开口越大.
1.求抛物线标准方程
当焦点在x轴上,开口方向不定时,设为y2=2mx(m ≠0),
当焦点在y轴上,开口方向不定时,设为x2=2my (m≠0),可避免讨论.
解:由已知可设抛物线的标准方程为y2=2px(p>0)
因此所求方程为:y2=4x
典例1
2.求焦点弦长
斜率为1的直线经过抛物线 y2=4x的焦点F,且与抛物线相交于两点A、B,求焦点弦长AB的长.
典例2
x2-6x+1=0
(x1, y1)
(x2, y2)
斜率为1的直线经过抛物线 y2=4x的焦点F,且与抛物线相交于两点A、B,求焦点弦长AB的长.
典例2
斜率为1的直线经过抛物线 y2=4x的焦点F,且与抛物线相交于两点A、B,求焦点弦长AB的长.
典例2
直线和抛物线的位置关系有三种:相交、相切、相离
将直线方程和抛物线方程联立,消元转化为关于 x(或 y 的)
方程组:
Ax2 + Bx + C = 0(或Ay2 + By + C = 0),其中A,B,C 为常数.
若A = 0,则直线和抛物线相交(直线与抛物线的对称轴平行),有一个交点;
若A ≠ 0,计算判别式 Δ=B2 -4AC :
若 Δ>0,则直线和抛物线相交(有两个交点);
若 Δ = 0,则直线和抛物线相切(有一个交点);
若 Δ<0,则直线和抛物线相离(无交点).
归纳总结
练一练
28
1. 求抛物线的对称轴
例5 经过抛物线焦点F的直线交抛物线于A,B两点,经过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.
思路:证明点D的纵坐标与点B的纵坐标相等即可.
O
l
F
A
x
y
B
D
O
l
F
A
x
y
B
D
所以,直线DB平行于抛物线的对称轴.
2.和抛物线有关的
轨迹方程
(1)求点P的轨迹方程;
解 过点P作x轴的垂线且垂足为点N,则|PN|=y,
故点P的轨迹方程为x2=2y.
练一练
(2)若直线l:y=kx+1与点P的轨迹相交于A,B两点,且|AB|= ,求实数k的值.
解 由题意设A(x1,y1),B(x2,y2),
∴x1+x2=2k,x1x2=-2.
∴k4+3k2-4=0,
又k2≥0,∴k2=1,∴k=±1.
3. 抛物线综合问题
如图,已知抛物线y2=4x的焦点为F,过点P(2,0)的直线交抛物线于A(x1,y1),B(x2,y2)两点,直线AF,BF分别与抛物线交于点M,N.
(1)求y1y2的值;
解 依题意,设AB的方程为x=my+2,
代入y2=4x,得y2-4my-8=0,从而y1y2=-8.
练一练
(2)连接MN,记直线MN的斜率为k1,直线AB的斜率为k2,证明: 为定值.
证明 设M(x3,y3),N(x4,y4),
设直线AM的方程为x=ny+1,
代入y2=4x,消去x得y2-4ny-4=0,
所以y1y3=-4,同理y2y4=-4,
解决抛物线综合问题的基本策略
对于抛物线的综合问题,可以从直线、抛物线的方程出发,结合解一元二次方程,经过逻辑推理和数学运算,从代数法的角度推证结论.
归纳总结
课堂练习
1.动点P(x,y)到点F(3,0)的距离比它到直线x+2=0的距离大1,则动点的轨迹是
A.椭圆 B.双曲线
C.双曲线的一支 D.抛物线
√
解析 依题意可知动点P(x,y)在直线x+2=0的右侧,
设P到直线x+2=0的距离为d,则|PF|=d+1,
所以动点P到F(3,0)的距离与到x+3=0的距离相等,
其轨迹为抛物线.
2.已知动圆M经过点A(3,0),且与直线l:x=-3相切,则动圆圆心M的轨迹方程为
A.y2=12x B.y2=-12x C.x2=12y D.x2=12y
√
解析 设动点M(x,y),⊙M与直线l:x=-3的切点为N,
则|MA|=|MN|,
即动点M到定点A和定直线l:x=-3的距离相等,
∴点M的轨迹是抛物线,且以A(3,0)为焦点,
以直线l:x=-3为准线,
故动圆圆心M的轨迹方程是y2=12x.
3.设A,B是抛物线x2=4y上两点,O为原点,若|OA|=|OB|,且△AOB的面积为16,则∠AOB等于
A.30° B.45° C.60° D.90°
√
解析 由|OA|=|OB|,知抛物线上点A,B关于y轴对称,
∴△AOB为等腰直角三角形,∠AOB=90°.
4.若直线x-y=2与抛物线y2=4x交于A,B两点,则线段AB的中点坐标是________.
(4,2)
设A(x1,y1),B(x2,y2),
则x1+x2=8,y1+y2=x1+x2-4=4,
故线段AB的中点坐标为(4,2).
y2=4x
即点N的轨迹方程是y2=4x.
随堂检测
当堂达标
图形 标准方程 焦点坐标 准线方程 焦点位置
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
四种抛物线及其标准方程
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
方程
图形
范围
对称性
顶点
焦半径
焦点弦
通径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0, y∈R
x≤0, y∈R
x∈R, y≥0
x∈R, y≤0
l
F
y
x
O
关于x轴对称
关于y轴对称
(0,0)
抛物线的简单几何性质
直线与抛物线的位置关系
设直线l:y=kx+m,抛物线:y2=2px(p>0),将直线方程与抛物线方程联立整理成关于x的方程k2x2+2(km-p)x+m2=0.
(1)若k≠0,当Δ>0时,直线与抛物线相交,有两个交点;
当Δ=0时,直线与抛物线相切,有一个切点;
当Δ<0时,直线与抛物线相离,没有公共点.
(2)若k=0,直线与抛物线有一个交点,此时直线平行于抛物线的对称轴或与对称轴重合.因此直线与抛物线有一个公共点是直线与抛物线相切的必要不充分条件.
【例1】 已知抛物线y2=8x.
(2)以坐标原点O为顶点,作抛物线的内接等腰三角形OAB,其中|OA|=|OB|.若焦点F是△OAB的重心,求△OAB的周长.
优化设计大本
(2)如图所示.由|OA|=|OB|可知AB⊥x轴,设垂足为点M.
因为焦点F是△OAB的重心,
变式训练4
已知抛物线的方程是y2=4x,直线l交抛物线于A,B两点,设A(x1,y1),B(x2,y2).
(1)若弦AB的中点为(3,3),求直线l的方程;
(2)若y1y2=-12,求证:直线l过定点.
(2)证明 当l的斜率存在时,易知k≠0,设l的方程为y=kx+b,代入抛物线方程,整理,得ky2-4y+4b=0,y1y2= =-12,b=-3k,
l的方程为y=kx-3k=k(x-3),过定点(3,0).
当l的斜率不存在时,y1y2=-12,则x1=x2=3,l过定点(3,0).综上,l过定点(3,0).
优化设计小本
优化设计小本
优化设计小本
优化设计小本
优化设计小本
THANKS
“
”
第 3 章圆锥曲线的方程
人教A版2019选修第一册
3.3.2 抛物线的简单几何性质
其中定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线
定义告诉我们:
(1)判断抛物线的一种方法
(2)抛物线上任一点的性质:|MF|=d
1.抛物线的定义
平面内与一个定点F 和一条定直线l (l 不经过点F)的距离相等的点的轨迹叫做抛物线.
┑
l
F
M
d
H
知识回顾
图形 标准方程 焦点坐标 准线方程 焦点位置
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
2.四种抛物线及其标准方程
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
由抛物线 y2 =2px(p>0)
有
所以抛物线的范围为
如何研究抛物线y2 =2px(p>0)的几何性质
1.范围
x
l
F
y
O
新知探究
关于x轴对称
即点(x,-y)也在抛物线上,
故抛物线y2 =2px(p>0)关于x轴对称.
则(-y)2 = 2px ,
若点(x,y)在抛物线上, 即满足y2 = 2px,
2.对称性
x
l
F
(x,y)
y
O
(x,-y)
定义:抛物线与它的轴的交点叫做抛物线的顶点.
∴ y2 =2px(p>0)中,令y=0,则x=0.
即抛物线y2 =2px(p>0)的顶点(0,0).
3.顶点
x
l
F
y
O
由定义知, 抛物线y2 =2px(p>0)的离心率为e=1.
4.离心率
x
┑
l
F
M
d
H
y
O
抛物线上的点M与焦点F的距离和它到准线的距离d之比 ,叫做抛物线的离心率,用e表示.
连接抛物线任意一点与焦点的线段叫做抛物线的焦半径.
焦半径公式:
5.焦半径
x
l
F
M
y
O
(x0,y0)
过抛物线的焦点的线段,叫做抛物线的焦点弦.
焦点弦公式:
6.焦点弦
x
l
F
A
y
O
B
(x1,y1)
(x2,y2)
A
B
y2=2px
2p
过焦点而垂直于对称轴的弦AB,称为抛物线的通径.
|AB|=2p
2p越大,抛物线张口越大
7.通径
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
x
l
F
y
O
方程
图形
范围
对称性
顶点
焦半径
焦点弦
通径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0, y∈R
x≤0, y∈R
x∈R, y≥0
x∈R, y≤0
l
F
y
x
O
关于x轴对称
关于y轴对称
(0,0)
抛物线的简单几何性质
如图,已知线段AB是抛物线y2=2px(p>0)的焦点弦,且A(x1,y1),B(x2,y2),点F是抛物线的焦点,过A,B两点分别作准线l的垂线AC,BD,垂足分别为点C,D,点M为线段AB的中点,点M′为线段CD的中点.
【方法技巧与总结】
点P(x0,y0)与抛物线y2=2px(p>0)的关系
(1)P在抛物线内(含焦点).
(2)P在抛物线上.
(3)P在抛物线外.
p的几何意义
p为焦点到准线l的距离,即焦准距,
p越大,抛物线开口越大.
1.求抛物线标准方程
当焦点在x轴上,开口方向不定时,设为y2=2mx(m ≠0),
当焦点在y轴上,开口方向不定时,设为x2=2my (m≠0),可避免讨论.
解:由已知可设抛物线的标准方程为y2=2px(p>0)
因此所求方程为:y2=4x
典例1
2.求焦点弦长
斜率为1的直线经过抛物线 y2=4x的焦点F,且与抛物线相交于两点A、B,求焦点弦长AB的长.
典例2
x2-6x+1=0
(x1, y1)
(x2, y2)
斜率为1的直线经过抛物线 y2=4x的焦点F,且与抛物线相交于两点A、B,求焦点弦长AB的长.
典例2
斜率为1的直线经过抛物线 y2=4x的焦点F,且与抛物线相交于两点A、B,求焦点弦长AB的长.
典例2
直线和抛物线的位置关系有三种:相交、相切、相离
将直线方程和抛物线方程联立,消元转化为关于 x(或 y 的)
方程组:
Ax2 + Bx + C = 0(或Ay2 + By + C = 0),其中A,B,C 为常数.
若A = 0,则直线和抛物线相交(直线与抛物线的对称轴平行),有一个交点;
若A ≠ 0,计算判别式 Δ=B2 -4AC :
若 Δ>0,则直线和抛物线相交(有两个交点);
若 Δ = 0,则直线和抛物线相切(有一个交点);
若 Δ<0,则直线和抛物线相离(无交点).
归纳总结
练一练
28
1. 求抛物线的对称轴
例5 经过抛物线焦点F的直线交抛物线于A,B两点,经过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.
思路:证明点D的纵坐标与点B的纵坐标相等即可.
O
l
F
A
x
y
B
D
O
l
F
A
x
y
B
D
所以,直线DB平行于抛物线的对称轴.
2.和抛物线有关的
轨迹方程
(1)求点P的轨迹方程;
解 过点P作x轴的垂线且垂足为点N,则|PN|=y,
故点P的轨迹方程为x2=2y.
练一练
(2)若直线l:y=kx+1与点P的轨迹相交于A,B两点,且|AB|= ,求实数k的值.
解 由题意设A(x1,y1),B(x2,y2),
∴x1+x2=2k,x1x2=-2.
∴k4+3k2-4=0,
又k2≥0,∴k2=1,∴k=±1.
3. 抛物线综合问题
如图,已知抛物线y2=4x的焦点为F,过点P(2,0)的直线交抛物线于A(x1,y1),B(x2,y2)两点,直线AF,BF分别与抛物线交于点M,N.
(1)求y1y2的值;
解 依题意,设AB的方程为x=my+2,
代入y2=4x,得y2-4my-8=0,从而y1y2=-8.
练一练
(2)连接MN,记直线MN的斜率为k1,直线AB的斜率为k2,证明: 为定值.
证明 设M(x3,y3),N(x4,y4),
设直线AM的方程为x=ny+1,
代入y2=4x,消去x得y2-4ny-4=0,
所以y1y3=-4,同理y2y4=-4,
解决抛物线综合问题的基本策略
对于抛物线的综合问题,可以从直线、抛物线的方程出发,结合解一元二次方程,经过逻辑推理和数学运算,从代数法的角度推证结论.
归纳总结
课堂练习
1.动点P(x,y)到点F(3,0)的距离比它到直线x+2=0的距离大1,则动点的轨迹是
A.椭圆 B.双曲线
C.双曲线的一支 D.抛物线
√
解析 依题意可知动点P(x,y)在直线x+2=0的右侧,
设P到直线x+2=0的距离为d,则|PF|=d+1,
所以动点P到F(3,0)的距离与到x+3=0的距离相等,
其轨迹为抛物线.
2.已知动圆M经过点A(3,0),且与直线l:x=-3相切,则动圆圆心M的轨迹方程为
A.y2=12x B.y2=-12x C.x2=12y D.x2=12y
√
解析 设动点M(x,y),⊙M与直线l:x=-3的切点为N,
则|MA|=|MN|,
即动点M到定点A和定直线l:x=-3的距离相等,
∴点M的轨迹是抛物线,且以A(3,0)为焦点,
以直线l:x=-3为准线,
故动圆圆心M的轨迹方程是y2=12x.
3.设A,B是抛物线x2=4y上两点,O为原点,若|OA|=|OB|,且△AOB的面积为16,则∠AOB等于
A.30° B.45° C.60° D.90°
√
解析 由|OA|=|OB|,知抛物线上点A,B关于y轴对称,
∴△AOB为等腰直角三角形,∠AOB=90°.
4.若直线x-y=2与抛物线y2=4x交于A,B两点,则线段AB的中点坐标是________.
(4,2)
设A(x1,y1),B(x2,y2),
则x1+x2=8,y1+y2=x1+x2-4=4,
故线段AB的中点坐标为(4,2).
y2=4x
即点N的轨迹方程是y2=4x.
随堂检测
当堂达标
图形 标准方程 焦点坐标 准线方程 焦点位置
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
四种抛物线及其标准方程
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
方程
图形
范围
对称性
顶点
焦半径
焦点弦
通径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0, y∈R
x≤0, y∈R
x∈R, y≥0
x∈R, y≤0
l
F
y
x
O
关于x轴对称
关于y轴对称
(0,0)
抛物线的简单几何性质
直线与抛物线的位置关系
设直线l:y=kx+m,抛物线:y2=2px(p>0),将直线方程与抛物线方程联立整理成关于x的方程k2x2+2(km-p)x+m2=0.
(1)若k≠0,当Δ>0时,直线与抛物线相交,有两个交点;
当Δ=0时,直线与抛物线相切,有一个切点;
当Δ<0时,直线与抛物线相离,没有公共点.
(2)若k=0,直线与抛物线有一个交点,此时直线平行于抛物线的对称轴或与对称轴重合.因此直线与抛物线有一个公共点是直线与抛物线相切的必要不充分条件.
【例1】 已知抛物线y2=8x.
(2)以坐标原点O为顶点,作抛物线的内接等腰三角形OAB,其中|OA|=|OB|.若焦点F是△OAB的重心,求△OAB的周长.
优化设计大本
(2)如图所示.由|OA|=|OB|可知AB⊥x轴,设垂足为点M.
因为焦点F是△OAB的重心,
变式训练4
已知抛物线的方程是y2=4x,直线l交抛物线于A,B两点,设A(x1,y1),B(x2,y2).
(1)若弦AB的中点为(3,3),求直线l的方程;
(2)若y1y2=-12,求证:直线l过定点.
(2)证明 当l的斜率存在时,易知k≠0,设l的方程为y=kx+b,代入抛物线方程,整理,得ky2-4y+4b=0,y1y2= =-12,b=-3k,
l的方程为y=kx-3k=k(x-3),过定点(3,0).
当l的斜率不存在时,y1y2=-12,则x1=x2=3,l过定点(3,0).综上,l过定点(3,0).
优化设计小本
优化设计小本
优化设计小本
优化设计小本
优化设计小本
THANKS
“
”
