1.3空间向量及其运算的坐标表示 课件(共34张PPT)
文档属性
| 名称 | 1.3空间向量及其运算的坐标表示 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 09:16:43 | ||
图片预览










文档简介
1.3 空间向量及其运算的坐标表示
知识回顾
1.在平面直角坐标系中,如何表示向量?
一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标
2.平面向量的加减运算如何用坐标表示?
3.平面向量的数乘运算如何用坐标表示?
4.平面向量的数量积如何用坐标表示?
两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差)
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标
两个向量的数量积等于它们对应坐标的乘积的和
知识回顾
5.平面向量的模如何用坐标表示?
6.平面向量的夹角余弦值如何用坐标表示?
我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法…….”
吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.
在平面向量中,我们以平面直角坐标系中与x 轴,y 轴方向相同的两个单位向量 , 为基底,建立了向量的坐标与点的坐标的一一对应关系,从而把平面向量的运算转化为坐标的运算.
类似地,能否利用空间向量基本定理和空
间的单位正交基底,建立空间直角坐标系,
进而建立空间向量的坐标与空间点的坐标
的一一对应呢?
空间直角坐标系
在空间选定一点O 和一个单位正交基底 ,以点O 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度,建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点, , , 叫做坐标向量,
通过每两条坐标轴的平面叫做坐标平面,
分别称为Oxy平面,Oyz平面,Ozx平面,
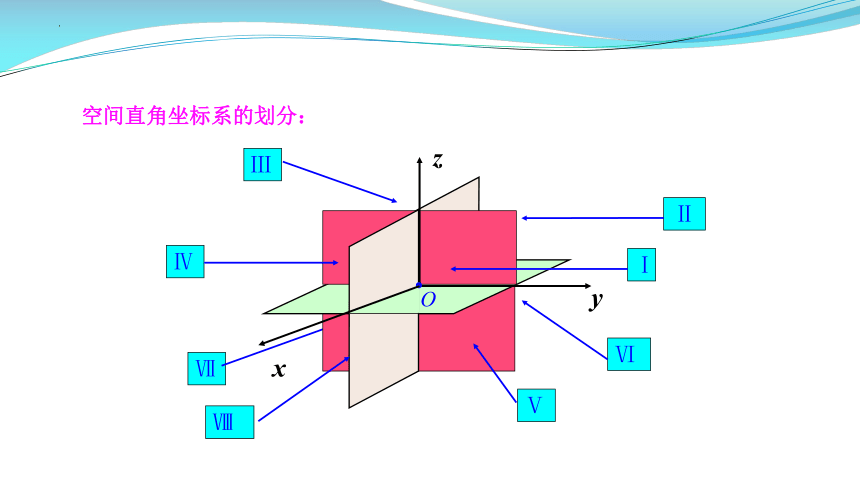
它们把空间分成八个部分.
Ⅱ
Ⅶ
Ⅴ
Ⅵ
Ⅰ
Ⅲ
Ⅳ
Ⅷ
?
O
空间直角坐标系的划分:
空间直角坐标系的画法
(1)画空间直角坐标系Oxyz时,一般使∠xOy =135°(或45°),
∠yOz =90°.
(2)直角坐标系右手定则:
在空间直角坐标系中,握住右手,四指向手心方向折合,从x 的方向沿小于180°的角转向y 轴,大拇指的方向就是z 轴.
在空间直角坐标系Oxyz中, , , 为坐标向量,对空间任意一点A,对应一个向量 ,且点A 的位置由向量 唯一确定,由空间向量基本定理,存在唯一的有序数组(x,y,z),使 .
在单位正交基底 下与向量对应
的有序数组(x,y,z),叫做点A在空间直
角坐标系中的坐标,记作A(x,y,z),其
中x 叫做点A 的横坐标、y 叫做点A 纵坐标、
z 叫做点A 竖坐标.
在空间直角坐标系Oxyz中,给定向量 ,作 ,由空间向量基本定理,存在唯一的有序数组(x,y,z),使 .
有序实数组(x,y,z)叫做 在空间直角坐标系Oxyz中的坐标,上式可简记作 . 这样,在空间直角
坐标系中,空间中的点和向量都可以用三
个有序实数表示.
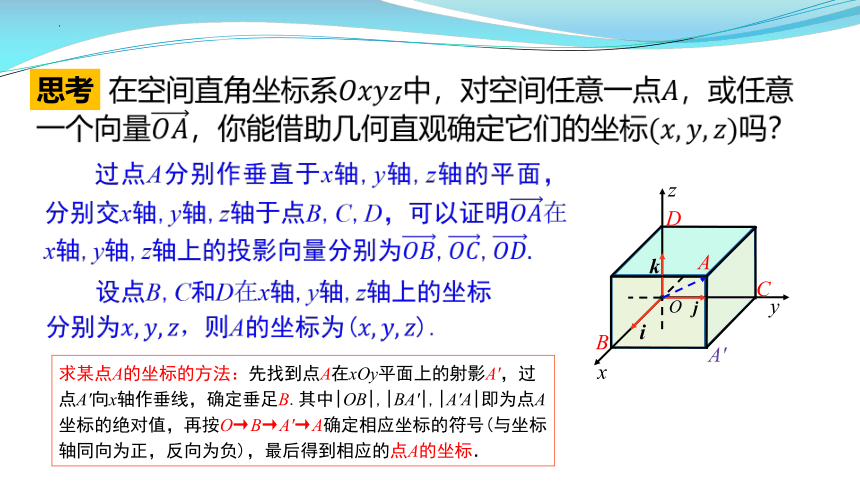
思考
在空间直角坐标系????????????????中,对空间任意一点????,或任意一个向量????????,你能借助几何直观确定它们的坐标(????,????,????)吗?
?
j
i
O
k
x
y
z
A
B
C
D
A'
过点A分别作垂直于x轴,y轴,z轴的平面,分别交x轴,y轴,z轴于点B,C,D,可以证明????????在x轴,y轴,z轴上的投影向量分别为????????,????????,????????.
?
设点B,C和D在x轴,y轴,z轴上的坐标分别为????,????,????,则A的坐标为(????,????,????).
?
求某点A的坐标的方法:先找到点A在xOy平面上的射影A',过点A'向x轴作垂线,确定垂足B.其中|OB|,|BA'|,|A'A|即为点A坐标的绝对值,再按O→B→A'→A确定相应坐标的符号(与坐标轴同向为正,反向为负),最后得到相应的点A的坐标.
O
x
y
z
A
B
C
B′
A′
C′
D′
解: (1) D'(0,0, 2),C(0,4,0),A'(3,0, 2),B'(3,4, 2)
例题1
空间直角坐标系中一些特殊的点
1.空间直角坐标系中坐标轴、坐标平面上的点的坐标
点的位置
x轴上
y轴上
z轴上
坐标形式
(x,0,0)
(0,y,0)
(0,0,z)
点的位置
Oxy平面
Oyz平面
Ozx平面
坐标形式
(x,y,0)
(0,y,z)
(x,0,z)
空间直角坐标系中一些特殊的点
2.空间直角坐标系中对称点的坐标(关于谁对称,谁保持不变,其余坐标相反)
(1)点(a,b,c)关于原点O的对称点为(-a,-b,-c);
(2)点(a,b,c)关于x轴的对称点为(a,-b,-c);
(3)点(a,b,c)关于y轴的对称点为(-a,b,-c);
(4)点(a,b,c)关于z轴的对称点为(-a,-b,c);
(5)点(a,b,c)关于Oxy平面的对称点为(a,b,-c);
(6)点(a,b,c)关于Oyz平面的对称点为(-a,b,c);
(7)点(a,b,c)关于Ozx平面的对称点为(a,-b,c).
空间中点坐标公式和重心坐标公式
在空间直角坐标系中,点 和点 的中点坐标为:
在空间直角坐标系中,已知点 ,点 ,点
,则△ABC的重心坐标为:
知识点2 空间向量及其运算的坐标表示
【复习回顾】已知 ????=(????1,????1),????=(????2,????2),平面向量的运算是如何利用坐标表示的?
【提示】 ????+????=(????1+????2,????1+????2) ; ????-????=(????1-????2,????1-????2);λ ????=(λ????1,λ????1); ?????????=????1????2+????1????2
????//???? ?????1????2?????1????2=0; ????⊥?????????1????2+????1????2=0 ; cos????,???? = ?????????????????=????1????2+????1????2????12+????12????22+????22
?
◆若????=(a1,a2,a3),????=(b1,b2,b3),则
(1)????+????= .
(2)????-????= .
(3)λ????= (λ∈R).
(4)????·????= .
?
????=(a1,a2,a3)=a1i+a2j+a3k,????=(b1,b2,b3)=b1i+b2j+b3k,所以 ????·????=(a1i+a2j+a3k)·(b1i+b2j+b3k)=a1b1i2+a2b2j2+a3b3k2+a1b2i·j+a1b3i·k+a2b1j·i+a2b3j·k+a3b1k·i+a3b2k·j
=a1b1+a2b2+a3b3.即a·b=a1b1+a2b2+a3b3.
?
数量积坐标运算的推导:
空间向量及其运算的坐标表示:
(a1+b1,a2+b2,a3+b3)
(a1-b1,a2-b2,a3-b3)
(λa1,λa2,λa3)
a1b1+a2b2+a3b3
(5)若????≠0,则 ????∥????? ????=λ?????a1=λb1,a2=λb2,a3=λb3(λ∈R).
(6)若 ????⊥????,则有 .
(7)| ????|=????2= .
(8) cos????,???? = ?????????????????= .
?
a1b1+a2b2+a3b3=0
????12+????22+????32
?
a1b1+a2b2+a3b3????12+????22+????32????12+????22+????32
?
知识点3 空间两点之间的距离公式
◆ 设P1(x1,y1,z1),P2(x2,y2,z2)是空间中任意两点,则
(1) ????1????2= .
(2)| ????1????2|= .
?
(x2-x1,y2-y1,z2-z1)
x2-x12+y2-y12+z2-z12
?
用终点B的坐标减去起点A的坐标,可得向量????????的坐标。
?
例题2
证明:不妨设正方体的棱长为1,建立如图所示的空间
直角坐标系
,则
所以
又
所以
所以
因此
,即 .
例题3 如图,正方体ABCD-A1B1C1D1,点E,F分别是BB1, D1B1的中点,求证:EF⊥DA1.
C
A
B
D
O
x
y
z
总结 向量平行与垂直问题的两种类型
(1)平行与垂直的判断.
①应用向量的方法判定两直线平行,只需判断两直线的方向向量是否共线.
②判断两直线是否垂直,关键是判断两直线的方向向量是否垂直,即判断两向量的数量积是否为0.
(2)平行与垂直的应用.
①适当引入参数(比如向量a,b平行,可设a=λb),建立关于参数的方程.
②选择坐标形式,以达到简化运算的目的.
例题4 如图,在棱长为1的正方体ABCD-A1B1C1D1,M为BC1的中点,E1,F1分别在棱A1B1,C1D1上,
(1)求AM的长.
(2)求
与
所成角的余弦值.
C
A
B
D
O
x
y
z
解:(1)建立如图的空间直角坐标系
,则
点
的坐标为
点
的坐标为 .
于是 .
M
(2)由已知得,
所以 .
所以 .
与
所成角的余弦值 .
所以
所以,
.
C
A
B
D
O
x
y
z
M
总结 运用空间向量的坐标运算解决立体几何问题的一般步骤
(1)建系:根据题目中的几何图形建立恰当的空间直角坐标系;
(2)求坐标:①求出相关点的坐标;②写出向量的坐标;
(3)论证、计算:结合公式进行论证、计算;
(4)转化:转化为几何结论.
例1.如图,在直三棱柱ABC?A1B1C1的底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别为A1B1,A1A的中点,以????????,????????,12????????1为单位正交基底,建立如图所示的空间直角坐标系C?xyz.
(1)写出B,C1,B1,M,N五点的坐标;
(2)写出向量????????,????????1, ????1???? 的坐标.
?
(2)????????=????????-????????=12????????1+????????-????????=i-j+k=(1,-1,1),
????????1=????????1-????????=????????????????+????????1=i-j+2k=(1,-1,2).
????1????=-????????1=(-1,1,-2).
?
[解析] (1)点B在y轴上,且CB=1,所以????????=0i+j+0k,所以点B的坐标是(0,1,0).同理,点C1的坐标为(0,0,2).
点B1在x轴、y轴、z轴上的射影分别为C,B,C1,它们在坐标轴上的坐标分别为0,1,2,所以点B1的坐标是(0,1,2).
同理,点M的坐标为(12,12,2),点N的坐标为(1,0,1).
?
跟踪训练
跟踪训练
例2. 已知空间四点A,B,C,D的坐标分别是(-1,2,1),(1,3,4),(0,-1,4),(2,-1,-2).
若????=????????,????=????????,
求下列各式的值:
(1)????+2????;(2)3????-????;
(3)(????-????)·(????+????);
(4)cos〈????,????〉.
?
[解析] 由于A(-1,2,1),B(1,3,4),C(0,-1,4),D(2,-1,-2),所以????=????????=(2,1,3),????=????????=(2,0,-6).
(1)????+2????=(2,1,3)+2(2,0,-6)=(2,1,3)+(4,0,-12)
=(6,1,-9).
(2)3????-????=3(2,1,3)-(2,0,-6)
=(6,3,9)-(2,0,-6)=(4,3,15).
(3)(????-????)·(????+????)=p2-q2=|p|2-|q|2
=(22+12+32)-[22+02+(-6)2]=-26.
(4)cos〈????,????〉=?????????????????=2×2+1×0+3×?622+12+3222+02+(-6)2
=?1414×210=-3510.
?
跟踪训练
【类题通法】1.一个向量的坐标等于表示这个向量的有向线段的终点坐标减去起点坐标.
2.在确定了向量的坐标后,使用空间向量的加减、数乘、数量积的坐标运算公式进行计算就可以了,但要熟练应用下列有关乘法公式:(1)(a+b)2=a2+2a·b+b2;(2)(a+b)·(a-b)=a2-b2.
【巩固练习2】1.已知 ????=(1,-2,1),?????????=(-1,2,-1),则 ???? =( )
A.(2,-4,2) B.(-2,4,-2) C.(-2,0,-2) D.(2,1,-3)
?
【解析】 ????= ????-(?????????)=(1,-2,1)-(-1,2,-1)=(2,-4,2) .故选:A
?
跟踪训练
例3.如图所示,正方体ABCD?A1B1C1D1的棱长为1,E是棱D1D的中点,P,Q分别为线段B1D1,BD上的点,且3 ????1????=????????1,以D为坐标原点,DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系.若PQ⊥AE,求点Q的坐标.
?
【解析】 由题图可知:A(1,0,0),E,B(1,1,0),B1(1,1,1),D1(0,0,1),
由题意,可设点P的坐标为(a,a,1),
因为3 ????1????=????????1,所以3(a-1,a-1,0)=(-a,-a,0),
所以3a-3=-a,解得a=34,所以点P的坐标为 34,34,1.
由题意可设点Q的坐标为(b,b,0),
因为PQ⊥AE,所以 ????????· ????????=0,所以 ?????34,?????34,?1·?1,0,12=0,
即-?????34-12=0,解得b=14,所以点Q的坐标为14,14,0.
?
跟踪训练
【变式探究1】本例中若G是A1D的中点,点H在平面xDy上,且GH∥BD1,试判断点H的位置.
【解析】 因为G是A1D的中点,所以点G的坐标为(12,0,12),
因为点H在平面xDy上,设点H的坐标为(m,n,0),
因为 ????????=(m,n,0)-(12,0,12)=(m-12,n,-12),
????????1=(0,0,1)-(1,1,0)=(-1,-1,1)且 ????????∥????????1,
所以 m-12?1=?????1=?121,解得m=1,n=12.
所以点H的坐标为(1,12,0),所以H为线段AB的中点.
?
例3.如图所示,正方体ABCD?A1B1C1D1的棱长为1,E是棱D1D的中点,P,Q分别为线段B1D1,BD上的点,且3 ????1????=????????1,以D为坐标原点,DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系.若PQ⊥AE,求点Q的坐标.
?
跟踪训练
【巩固练习3】如图所示,在棱长为a的正方体ABCD?A1B1C1D1中,以D为坐标原点,DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系.过B作BM⊥AC1于M,求点M的坐标.
【解析】设M(x,y,z),由题图可知:A(a,0,0),B(a,a,0),C1(0,a,a),则????????1=(-a,a,a),????????=(x-a,y,z),????????=(x-a,y-a,z).
∵BM⊥AC1,∴???????? ·????????1=0,
∴-a(x-a)+a(y-a)+az=0,
即x-y-z=0.①
又∵????????1∥????????,∴x-a=-λa,y=λa,z=λa,
即x=a-λa,y=λa,z=λa.②
由①②得x=2????3,y=????3,z=????3 . ∴M 2????3,????3,????3.
?
跟踪训练
例4.在棱长为1的正方体ABCD?A1B1C1D1中,E,F分别是D1D,BD的中点,G在棱CD上,且CG=14CD,H是C1G的中点.
(1)求FH的长;
(2)求EF与C1G所成角的余弦值.
?
[解析] 如图所示,以DA,DC,DD1为单位正交基底建立空间直角坐标系Dxyz,则D(0,0,0),E(0,0,12),F(12,12,0),C(0,1,0),C1(0,1,1),B1(1,1,1),G(0,34,0).
?
(1)∵H是C1G的中点,∴H 0,78,12. 又F (12,12,0),∴FH=|????????|=0?122+78?122+12?02=418.
(2)∵ ????1????=0,?14,?1,则| ????1????|=174. 又|????????|=32,且 ????1???? ·????????=38,
∴cos〈????1????,????????〉=????1?????????????????1????????????=5117, 即EF与C1G所成角的余弦值为5117 .
?
跟踪训练
【巩固练习4】如图,在直三棱柱(侧棱垂直于底面的棱柱)ABC?A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,N为A1A的中点.
(1)求BN的长;
(2)求A1B与B1C所成角的余弦值.
【解析】如图,以????????,????????,12????????1为单位正交基底建立空间直角坐标系C?xyz.
(1)依题意得B(0,1,0),N(1,0,1),∴|????????|=1?02+0?12+1?02=3,
∴线段BN的长为 3.
(2)依题意得A1(1,0,2),C(0,0,0),B1(0,1,2),∴ ????????1=(1,-1,2),????????1=(0,1,2),
∴????????1 ·????????1=1×0+(-1)×1+2×2=3.
又|????????1|=6,|????????1|=5,∴cos〈????????1,????????1〉=????????1 ·????????1|????????1||????????1|= 3010.
故A1B与B1C所成角的余弦值为 3010 .
?
跟踪训练
THANKS
知识回顾
1.在平面直角坐标系中,如何表示向量?
一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标
2.平面向量的加减运算如何用坐标表示?
3.平面向量的数乘运算如何用坐标表示?
4.平面向量的数量积如何用坐标表示?
两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差)
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标
两个向量的数量积等于它们对应坐标的乘积的和
知识回顾
5.平面向量的模如何用坐标表示?
6.平面向量的夹角余弦值如何用坐标表示?
我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法…….”
吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.
在平面向量中,我们以平面直角坐标系中与x 轴,y 轴方向相同的两个单位向量 , 为基底,建立了向量的坐标与点的坐标的一一对应关系,从而把平面向量的运算转化为坐标的运算.
类似地,能否利用空间向量基本定理和空
间的单位正交基底,建立空间直角坐标系,
进而建立空间向量的坐标与空间点的坐标
的一一对应呢?
空间直角坐标系
在空间选定一点O 和一个单位正交基底 ,以点O 为原点,分别以 , , 的方向为正方向、以它们的长为单位长度,建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点, , , 叫做坐标向量,
通过每两条坐标轴的平面叫做坐标平面,
分别称为Oxy平面,Oyz平面,Ozx平面,
它们把空间分成八个部分.
Ⅱ
Ⅶ
Ⅴ
Ⅵ
Ⅰ
Ⅲ
Ⅳ
Ⅷ
?
O
空间直角坐标系的划分:
空间直角坐标系的画法
(1)画空间直角坐标系Oxyz时,一般使∠xOy =135°(或45°),
∠yOz =90°.
(2)直角坐标系右手定则:
在空间直角坐标系中,握住右手,四指向手心方向折合,从x 的方向沿小于180°的角转向y 轴,大拇指的方向就是z 轴.
在空间直角坐标系Oxyz中, , , 为坐标向量,对空间任意一点A,对应一个向量 ,且点A 的位置由向量 唯一确定,由空间向量基本定理,存在唯一的有序数组(x,y,z),使 .
在单位正交基底 下与向量对应
的有序数组(x,y,z),叫做点A在空间直
角坐标系中的坐标,记作A(x,y,z),其
中x 叫做点A 的横坐标、y 叫做点A 纵坐标、
z 叫做点A 竖坐标.
在空间直角坐标系Oxyz中,给定向量 ,作 ,由空间向量基本定理,存在唯一的有序数组(x,y,z),使 .
有序实数组(x,y,z)叫做 在空间直角坐标系Oxyz中的坐标,上式可简记作 . 这样,在空间直角
坐标系中,空间中的点和向量都可以用三
个有序实数表示.
思考
在空间直角坐标系????????????????中,对空间任意一点????,或任意一个向量????????,你能借助几何直观确定它们的坐标(????,????,????)吗?
?
j
i
O
k
x
y
z
A
B
C
D
A'
过点A分别作垂直于x轴,y轴,z轴的平面,分别交x轴,y轴,z轴于点B,C,D,可以证明????????在x轴,y轴,z轴上的投影向量分别为????????,????????,????????.
?
设点B,C和D在x轴,y轴,z轴上的坐标分别为????,????,????,则A的坐标为(????,????,????).
?
求某点A的坐标的方法:先找到点A在xOy平面上的射影A',过点A'向x轴作垂线,确定垂足B.其中|OB|,|BA'|,|A'A|即为点A坐标的绝对值,再按O→B→A'→A确定相应坐标的符号(与坐标轴同向为正,反向为负),最后得到相应的点A的坐标.
O
x
y
z
A
B
C
B′
A′
C′
D′
解: (1) D'(0,0, 2),C(0,4,0),A'(3,0, 2),B'(3,4, 2)
例题1
空间直角坐标系中一些特殊的点
1.空间直角坐标系中坐标轴、坐标平面上的点的坐标
点的位置
x轴上
y轴上
z轴上
坐标形式
(x,0,0)
(0,y,0)
(0,0,z)
点的位置
Oxy平面
Oyz平面
Ozx平面
坐标形式
(x,y,0)
(0,y,z)
(x,0,z)
空间直角坐标系中一些特殊的点
2.空间直角坐标系中对称点的坐标(关于谁对称,谁保持不变,其余坐标相反)
(1)点(a,b,c)关于原点O的对称点为(-a,-b,-c);
(2)点(a,b,c)关于x轴的对称点为(a,-b,-c);
(3)点(a,b,c)关于y轴的对称点为(-a,b,-c);
(4)点(a,b,c)关于z轴的对称点为(-a,-b,c);
(5)点(a,b,c)关于Oxy平面的对称点为(a,b,-c);
(6)点(a,b,c)关于Oyz平面的对称点为(-a,b,c);
(7)点(a,b,c)关于Ozx平面的对称点为(a,-b,c).
空间中点坐标公式和重心坐标公式
在空间直角坐标系中,点 和点 的中点坐标为:
在空间直角坐标系中,已知点 ,点 ,点
,则△ABC的重心坐标为:
知识点2 空间向量及其运算的坐标表示
【复习回顾】已知 ????=(????1,????1),????=(????2,????2),平面向量的运算是如何利用坐标表示的?
【提示】 ????+????=(????1+????2,????1+????2) ; ????-????=(????1-????2,????1-????2);λ ????=(λ????1,λ????1); ?????????=????1????2+????1????2
????//???? ?????1????2?????1????2=0; ????⊥?????????1????2+????1????2=0 ; cos????,???? = ?????????????????=????1????2+????1????2????12+????12????22+????22
?
◆若????=(a1,a2,a3),????=(b1,b2,b3),则
(1)????+????= .
(2)????-????= .
(3)λ????= (λ∈R).
(4)????·????= .
?
????=(a1,a2,a3)=a1i+a2j+a3k,????=(b1,b2,b3)=b1i+b2j+b3k,所以 ????·????=(a1i+a2j+a3k)·(b1i+b2j+b3k)=a1b1i2+a2b2j2+a3b3k2+a1b2i·j+a1b3i·k+a2b1j·i+a2b3j·k+a3b1k·i+a3b2k·j
=a1b1+a2b2+a3b3.即a·b=a1b1+a2b2+a3b3.
?
数量积坐标运算的推导:
空间向量及其运算的坐标表示:
(a1+b1,a2+b2,a3+b3)
(a1-b1,a2-b2,a3-b3)
(λa1,λa2,λa3)
a1b1+a2b2+a3b3
(5)若????≠0,则 ????∥????? ????=λ?????a1=λb1,a2=λb2,a3=λb3(λ∈R).
(6)若 ????⊥????,则有 .
(7)| ????|=????2= .
(8) cos????,???? = ?????????????????= .
?
a1b1+a2b2+a3b3=0
????12+????22+????32
?
a1b1+a2b2+a3b3????12+????22+????32????12+????22+????32
?
知识点3 空间两点之间的距离公式
◆ 设P1(x1,y1,z1),P2(x2,y2,z2)是空间中任意两点,则
(1) ????1????2= .
(2)| ????1????2|= .
?
(x2-x1,y2-y1,z2-z1)
x2-x12+y2-y12+z2-z12
?
用终点B的坐标减去起点A的坐标,可得向量????????的坐标。
?
例题2
证明:不妨设正方体的棱长为1,建立如图所示的空间
直角坐标系
,则
所以
又
所以
所以
因此
,即 .
例题3 如图,正方体ABCD-A1B1C1D1,点E,F分别是BB1, D1B1的中点,求证:EF⊥DA1.
C
A
B
D
O
x
y
z
总结 向量平行与垂直问题的两种类型
(1)平行与垂直的判断.
①应用向量的方法判定两直线平行,只需判断两直线的方向向量是否共线.
②判断两直线是否垂直,关键是判断两直线的方向向量是否垂直,即判断两向量的数量积是否为0.
(2)平行与垂直的应用.
①适当引入参数(比如向量a,b平行,可设a=λb),建立关于参数的方程.
②选择坐标形式,以达到简化运算的目的.
例题4 如图,在棱长为1的正方体ABCD-A1B1C1D1,M为BC1的中点,E1,F1分别在棱A1B1,C1D1上,
(1)求AM的长.
(2)求
与
所成角的余弦值.
C
A
B
D
O
x
y
z
解:(1)建立如图的空间直角坐标系
,则
点
的坐标为
点
的坐标为 .
于是 .
M
(2)由已知得,
所以 .
所以 .
与
所成角的余弦值 .
所以
所以,
.
C
A
B
D
O
x
y
z
M
总结 运用空间向量的坐标运算解决立体几何问题的一般步骤
(1)建系:根据题目中的几何图形建立恰当的空间直角坐标系;
(2)求坐标:①求出相关点的坐标;②写出向量的坐标;
(3)论证、计算:结合公式进行论证、计算;
(4)转化:转化为几何结论.
例1.如图,在直三棱柱ABC?A1B1C1的底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别为A1B1,A1A的中点,以????????,????????,12????????1为单位正交基底,建立如图所示的空间直角坐标系C?xyz.
(1)写出B,C1,B1,M,N五点的坐标;
(2)写出向量????????,????????1, ????1???? 的坐标.
?
(2)????????=????????-????????=12????????1+????????-????????=i-j+k=(1,-1,1),
????????1=????????1-????????=????????????????+????????1=i-j+2k=(1,-1,2).
????1????=-????????1=(-1,1,-2).
?
[解析] (1)点B在y轴上,且CB=1,所以????????=0i+j+0k,所以点B的坐标是(0,1,0).同理,点C1的坐标为(0,0,2).
点B1在x轴、y轴、z轴上的射影分别为C,B,C1,它们在坐标轴上的坐标分别为0,1,2,所以点B1的坐标是(0,1,2).
同理,点M的坐标为(12,12,2),点N的坐标为(1,0,1).
?
跟踪训练
跟踪训练
例2. 已知空间四点A,B,C,D的坐标分别是(-1,2,1),(1,3,4),(0,-1,4),(2,-1,-2).
若????=????????,????=????????,
求下列各式的值:
(1)????+2????;(2)3????-????;
(3)(????-????)·(????+????);
(4)cos〈????,????〉.
?
[解析] 由于A(-1,2,1),B(1,3,4),C(0,-1,4),D(2,-1,-2),所以????=????????=(2,1,3),????=????????=(2,0,-6).
(1)????+2????=(2,1,3)+2(2,0,-6)=(2,1,3)+(4,0,-12)
=(6,1,-9).
(2)3????-????=3(2,1,3)-(2,0,-6)
=(6,3,9)-(2,0,-6)=(4,3,15).
(3)(????-????)·(????+????)=p2-q2=|p|2-|q|2
=(22+12+32)-[22+02+(-6)2]=-26.
(4)cos〈????,????〉=?????????????????=2×2+1×0+3×?622+12+3222+02+(-6)2
=?1414×210=-3510.
?
跟踪训练
【类题通法】1.一个向量的坐标等于表示这个向量的有向线段的终点坐标减去起点坐标.
2.在确定了向量的坐标后,使用空间向量的加减、数乘、数量积的坐标运算公式进行计算就可以了,但要熟练应用下列有关乘法公式:(1)(a+b)2=a2+2a·b+b2;(2)(a+b)·(a-b)=a2-b2.
【巩固练习2】1.已知 ????=(1,-2,1),?????????=(-1,2,-1),则 ???? =( )
A.(2,-4,2) B.(-2,4,-2) C.(-2,0,-2) D.(2,1,-3)
?
【解析】 ????= ????-(?????????)=(1,-2,1)-(-1,2,-1)=(2,-4,2) .故选:A
?
跟踪训练
例3.如图所示,正方体ABCD?A1B1C1D1的棱长为1,E是棱D1D的中点,P,Q分别为线段B1D1,BD上的点,且3 ????1????=????????1,以D为坐标原点,DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系.若PQ⊥AE,求点Q的坐标.
?
【解析】 由题图可知:A(1,0,0),E,B(1,1,0),B1(1,1,1),D1(0,0,1),
由题意,可设点P的坐标为(a,a,1),
因为3 ????1????=????????1,所以3(a-1,a-1,0)=(-a,-a,0),
所以3a-3=-a,解得a=34,所以点P的坐标为 34,34,1.
由题意可设点Q的坐标为(b,b,0),
因为PQ⊥AE,所以 ????????· ????????=0,所以 ?????34,?????34,?1·?1,0,12=0,
即-?????34-12=0,解得b=14,所以点Q的坐标为14,14,0.
?
跟踪训练
【变式探究1】本例中若G是A1D的中点,点H在平面xDy上,且GH∥BD1,试判断点H的位置.
【解析】 因为G是A1D的中点,所以点G的坐标为(12,0,12),
因为点H在平面xDy上,设点H的坐标为(m,n,0),
因为 ????????=(m,n,0)-(12,0,12)=(m-12,n,-12),
????????1=(0,0,1)-(1,1,0)=(-1,-1,1)且 ????????∥????????1,
所以 m-12?1=?????1=?121,解得m=1,n=12.
所以点H的坐标为(1,12,0),所以H为线段AB的中点.
?
例3.如图所示,正方体ABCD?A1B1C1D1的棱长为1,E是棱D1D的中点,P,Q分别为线段B1D1,BD上的点,且3 ????1????=????????1,以D为坐标原点,DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系.若PQ⊥AE,求点Q的坐标.
?
跟踪训练
【巩固练习3】如图所示,在棱长为a的正方体ABCD?A1B1C1D1中,以D为坐标原点,DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系.过B作BM⊥AC1于M,求点M的坐标.
【解析】设M(x,y,z),由题图可知:A(a,0,0),B(a,a,0),C1(0,a,a),则????????1=(-a,a,a),????????=(x-a,y,z),????????=(x-a,y-a,z).
∵BM⊥AC1,∴???????? ·????????1=0,
∴-a(x-a)+a(y-a)+az=0,
即x-y-z=0.①
又∵????????1∥????????,∴x-a=-λa,y=λa,z=λa,
即x=a-λa,y=λa,z=λa.②
由①②得x=2????3,y=????3,z=????3 . ∴M 2????3,????3,????3.
?
跟踪训练
例4.在棱长为1的正方体ABCD?A1B1C1D1中,E,F分别是D1D,BD的中点,G在棱CD上,且CG=14CD,H是C1G的中点.
(1)求FH的长;
(2)求EF与C1G所成角的余弦值.
?
[解析] 如图所示,以DA,DC,DD1为单位正交基底建立空间直角坐标系Dxyz,则D(0,0,0),E(0,0,12),F(12,12,0),C(0,1,0),C1(0,1,1),B1(1,1,1),G(0,34,0).
?
(1)∵H是C1G的中点,∴H 0,78,12. 又F (12,12,0),∴FH=|????????|=0?122+78?122+12?02=418.
(2)∵ ????1????=0,?14,?1,则| ????1????|=174. 又|????????|=32,且 ????1???? ·????????=38,
∴cos〈????1????,????????〉=????1?????????????????1????????????=5117, 即EF与C1G所成角的余弦值为5117 .
?
跟踪训练
【巩固练习4】如图,在直三棱柱(侧棱垂直于底面的棱柱)ABC?A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,N为A1A的中点.
(1)求BN的长;
(2)求A1B与B1C所成角的余弦值.
【解析】如图,以????????,????????,12????????1为单位正交基底建立空间直角坐标系C?xyz.
(1)依题意得B(0,1,0),N(1,0,1),∴|????????|=1?02+0?12+1?02=3,
∴线段BN的长为 3.
(2)依题意得A1(1,0,2),C(0,0,0),B1(0,1,2),∴ ????????1=(1,-1,2),????????1=(0,1,2),
∴????????1 ·????????1=1×0+(-1)×1+2×2=3.
又|????????1|=6,|????????1|=5,∴cos〈????????1,????????1〉=????????1 ·????????1|????????1||????????1|= 3010.
故A1B与B1C所成角的余弦值为 3010 .
?
跟踪训练
THANKS
