5.1.2导数的概念及几何意义 课件(共57张PPT)
文档属性
| 名称 | 5.1.2导数的概念及几何意义 课件(共57张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 10:49:13 | ||
图片预览








文档简介
(共57张PPT)
5.1.2导数的概念及
几何意义
情境导入
下雨天,当我们将雨伞转动时,伞面边沿的水滴沿着伞的切线方向飞出.实际上物体(看作质点)做曲线运动时,运动方向在不停地变化,其速度方向为质点在其轨迹曲线上的切线方向,我们可以利用导数研究曲线的切线问题.
水滴沿伞边切线飞出
2019年国际田联钻石联赛伦敦站男子200米比赛,中国选手谢震业以19秒88夺冠,这不仅刷新了全国纪录,还创造了新的亚洲纪录.赛后各国教练都在研究他的弯道技术,通过回放录像分析其弯道时的运动方向.这需要求运动曲线在任一点的切线.怎样求曲线的切线?
观察函数f(x)的图象平均变化率
表示什么
O
A
B
x
y
y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
直线AB的斜率
思考
函数平均变化率的几何意义和物理意义
平均变化率的几何意义是表示函数y=f(x)图象上割线P1P2的斜率(其中P1(x1,f(x1)),P2(x2,f(x2))),
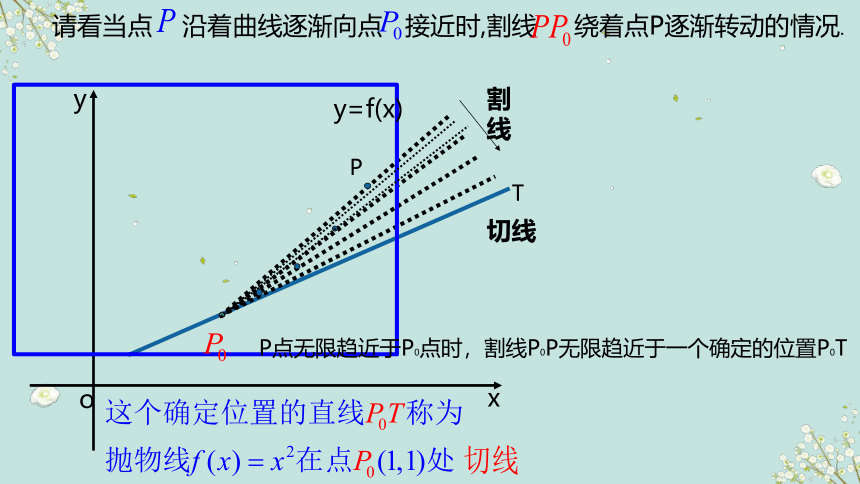
问题 抛物线的切线的斜率
P
o
x
y
y=f(x)
割线
切线
T
请看当点 沿着曲线逐渐向点 接近时,割线 绕着点P逐渐转动的情况.
P点无限趋近于P0点时,割线P0P无限趋近于一个确定的位置P0T
o
x
y
y=f(x)
P
割线
切线
T
h
t
o
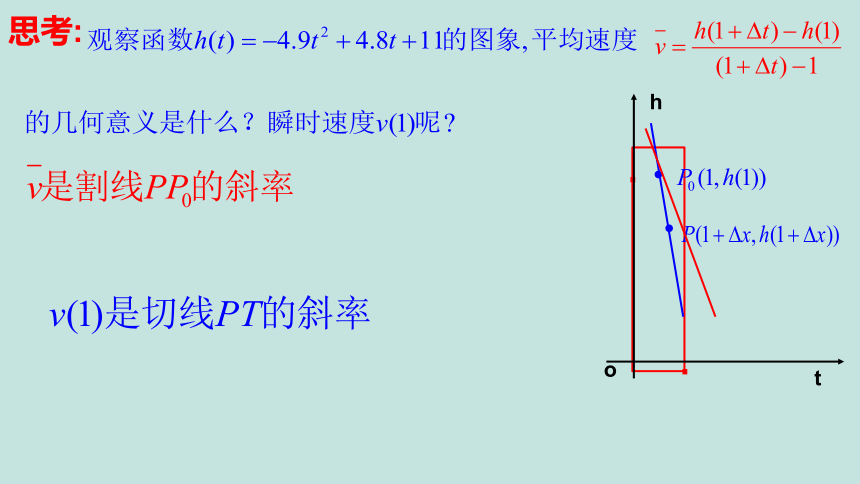
思考:
导数的概念
解析:
(1)Δy=2(3+Δx)2+4(3+Δx)-(2×32+4×3)
=12Δx+2(Δx)2+4Δx
=2(Δx)2+16Δx,
=2Δx+16.
=16.
=4x0+4,
∴f′(x0)=4x0+4=12,
解得x0=2.
求切点坐标可以按以下步骤进行
(1)设出切点坐标;
(2)利用导数或斜率公式求出斜率;
(3)利用斜率关系列方程,求出切点的横坐标;
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
=2x0+1,
又切线斜率为3即2x0+1=3,
∴x0=1,
则y0=0.
解析:设点M(x0,y0),
y′|x=3=32=9,
即曲线在P(3,9)处的切线的斜率等于9.
由直线的点斜式方程可得,所求切线方程为y-9=9(x-3),
即9x-y-18=0.
导数与函数图象升降的关系
例4 若函数y=f(x)的导函数在区间[a,b]上是增函数,
则函数y=f(x)在区间[a,b]上的图象可能是下图中的 ( )
[解析] 由导数的几何意义知导函数递增说明函数切线斜率随x增大而变大,因此应选A.
导数与函数图象升降的关系
若函数y=f(x)在x=x0处的导数存在且f′(x0)>0(即切线的斜率大于零),则函数y=f(x)在x=x0附近的图象是上升的;
若f′(x0)<0(即切线的斜率小于零),则函数y=f(x)在x=x0附近的图象是下降的.
导数绝对值的大小反映了曲线上升和下降的快慢.
曲线f(x)在x=x0附近的升降情况 切线的
斜率k 切线的
倾斜角
f′(x0)>0 上升 k>0 锐角
f′(x0)<0 下降 k<0 钝角
f′(x0)=0 平坦 k=0 零角(切线与x轴平行)
说明:切线斜率的绝对值的大小反映了曲线在相应点附近上升或下降的快慢.
巩固练习.已知函数y=f(x),y=g(x)的导函数的图象如图,
那么y=f(x),y=g(x)的图象可能是 ( )
从导函数的图象可知两个函数在x0处斜率相同,可以排除B、C.
再者导函数的函数值反映的是原函数的斜率大小,可明显看出y=f(x)的导函数的值在减小,所以原函数的斜率慢慢变小,排除A.
解析:点(5,f(5))在切线y=-x+8上,
∴f(5)=-5+8=3.
且k=f′(5)=-1
∴f(5)+f′(5)=2.
一、导数的概念
1.函数的平均变化率
对于函数y=f(x),设自变量x从x0变化到x0+Δx,相应地,函数值y就从f(x0)变化到f(x0+Δx),这时,x的变化量为Δx,y的变化量为Δy=f(x0+Δx)-f(x0).我们把比值 ,即 =______________________叫做函数y=f(x)从x0到x0+Δx的平均变化率.
y
x
y
x
2.函数在x=x0处的导数
如果当Δx→0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称y=f(x)在x=x0处可导,把这个确定的值叫做y=f(x)在x=x0处的导数(或瞬时变化率),记作f′(x0)或y′|x=x0,
y
x
y
x
对导数概念的再理解
(1)函数应在点x0的附近有定义,否则导数不存在;
(2)导数是一个局部概念,它只与函数y=f(x)在x=x0及其附近的函数值有关,与Δx无关;
(3)导数的实质是一个极限值.
二、导数的几何意义
导数f '(x)表示函数y=f(x)在x=x0处的瞬时变化率,反映了函数y=f(x)在x=x0附近的变化情况.那么导数的几何意义是什么?
平均变化率表示什么?
表示割线PP0的斜率
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
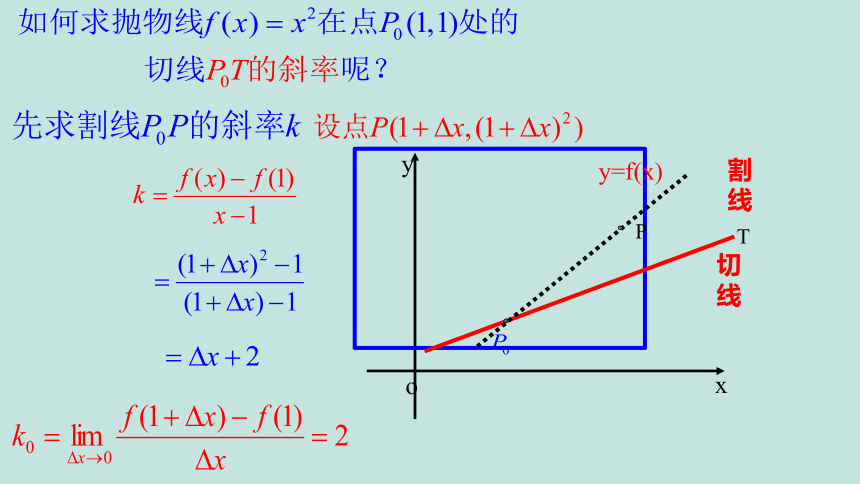
割线P0P 的斜率
当 时,k 无限接近函数
y=f(x)在x=x0的导数f '(x0)
导数的几何意义:f '(x)是函数 y=f(x) 在x=x0处切线P0T的斜率.
(1)曲线的切线与割线
①曲线的切线是由割线绕一点转动,当另一点无限接近这一点时割线趋于的直线.
②曲线的切线就是割线趋近于某一确定位置的直线,体现了无限趋近的思想.
(2)曲线的切线与导数
①函数f(x)在x=x0处有导数,则在该点处函数f(x)表示的曲线必有切线,且导数值是该切线的斜率.
②函数f(x)表示的曲线在点(x0,f(x0))处有切线,但函数f(x)在该点处不一定可导,如f(x)= 在x=0处有切线,但不可导.
曲线的切线并不一定与曲线只有一个交点,可以有多个,甚至可以有无穷多个.与曲线只有一个公共点的直线也不一定是曲线的切线.
3
三、导函数
对于函数y=f(x),当x=x0时,f′(x0)是一个确定的数,当x变化时,f′(x)便是一个关于x的函数,我们称它为函数y=f(x)的导函数(简称为导数),即f′(x)=y′=________________.
题型一
求函数在某点处的导数
简称:一差、二比、三极限
题型二
求曲线的切线方程
[例2] (链接教科书第70页练习2题)已知曲线C:y=x3.
(1)求曲线C在横坐标为x=1的点处的切线方程;
(2)求曲线C过点(1,1)的切线方程.
(1)将x=1代入曲线C的方程得y=1,∴切点P(1,1).
∴k=y′|x=1=3.
∴曲线在点P(1,1)处的切线方程为y-1=3(x-1),
即3x-y-2=0.
(2)设切点为Q(x0,y0),由(1)可知y′|x=x0=3x02,由题意可知kPQ=y′|x=x0,
①当x0=1时,切点坐标为(1,1),相应的切线方程为3x-y-2=0.
相应的切线方程为3x-4y+1=0.
求曲线y=x2+1过点P(1,0)的切线方程.
设切点为Q(a,a2+1),
∵在点Q处的切线方程为y-(a2+1)=2a(x-a),*
把点(1,0)代入(*)式得-(a2+1)=2a(1-a).
题型三
导数几何意义的应用
探究1 求切点坐标
例3 已知曲线y=x2+6的切线分别符合下列条件,求切点.
(1)平行于直线y=4x-3;
(2)垂直于直线2x-y+5=0.
设切点坐标为(x0,y0).f′(x)=
∴过(x0,y0)的切线的斜率为2x0.
(1)∵切线与直线y=4x-3平行,∴2x0=4,x0=2,y0=x02+6=10,
即过曲线y=x2+6上点(2,10)的切线与直线y=4x-3平行.
(2)∵切线与直线2x-y+5=0垂直,
∴2x0×2=-1,
即过曲线y=x2+6上点
的切线与直线2x-y+5=0垂直.
探究2 与曲线的切点相关的问题
例4 已知直线l1为曲线y=x2+x-2在(1,0)处的切线,l2为该曲线的另一条切线,且l1⊥l2.
(1)求直线l2的方程;
(2)求由直线l1,l2和x轴围成的三角形面积.
(1)y′=
所以y′|x=1=2×1+1=3,
所以直线l1的方程为y=3(x-1),即y=3x-3.
设直线l2过曲线y=x2+x-2上的点B(b,b2+b-2),
则l2的方程为y=(2b+1)x-b2-2.因为l1⊥l2,
1.如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.
o
x
y
P
5
点(5,f(5))在切线y=-x+8上,
∴f(5)=-5+8=3.
且f′(5)=-1,∴f(5)+f′(5)=2.
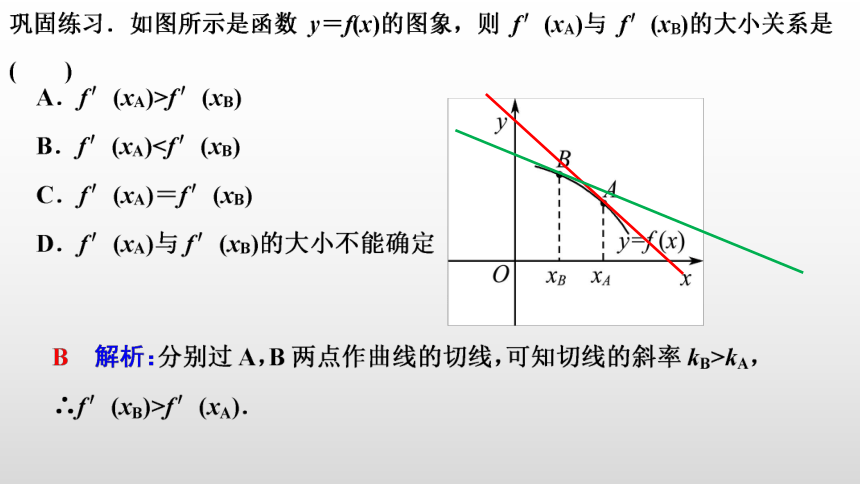
2.已知函数y=f(x)的图象如图,则f′(xA)与f′(xB)的大小关系是( )
A.0>f′(xA)>f′(xB) B.f′(xA)C.f′(xA)=f′(xB) D.f′(xA)>f′(xB)>0
o
x
y
B
A
3.李华在参加一次同学聚会时,用如图所示的圆口杯喝饮料,他想:如果向杯子中倒饮料的速度一定(即单位时间内倒入的饮料量相同),那么杯子中饮料的高度h是关于时间t的函数h(t),则函数h(t)的图象可能是 ( )
o
t
h
o
t
h
o
t
h
o
t
h
h0
h0
h0
h0
t0
t0
t0
t0
由于圆口杯是“下细上粗”,则开始饮料高度增加较快,以后饮料高度增加得越来越慢,仅有B符合.
A
B
C
D
1.导数的定义
如果当Δx→0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称y=f(x)在x=x0处可导,把这个确定的值叫做y=f(x)在x=x0处的导数(或瞬时变化率),记作f′(x0)或y′|x=x0,
y
x
y
x
2.导数的几何意义
曲线y=f(x)在点(x0,y0)的切线斜率为.
知识点1 过关自诊
1.判断正误.(正确的打√,错误的打×)
(4)函数的平均变化率越小,表示函数值变化得越慢.( )
×
优化设计大本
知识点3 过关自诊
1.判断正误.(正确的打√,错误的打×)
(2)直线与曲线相切,则直线与曲线只有一个公共点.( )
×
知识点4 过关自诊
1.判断正误.(正确的打√,错误的打×)
(3)f'(x0)=(f(x0))'.( )
×
探究点二
利用导数的定义求函数的导数
【例2】(1)求函数y=x- 在x=-1处的导数.
(2)求函数y=f(x)=-x2+3x的导数.
分析(1)可以直接利用函数在某一点处的导数的定义求解,也可先求出函数的导函数,再计算导函数在x=-1处的函数值;(2)可按照函数导数的定义分步求解.
探究点四
导数几何意义的应用
角度1求切线方程
【例4】已知曲线C:y=x3.
(1)求曲线C在横坐标为x=1的点处的切线方程;
(2)求曲线C过点P(1,1)的切线方程.
优化设计小本
5.1.2导数的概念及
几何意义
情境导入
下雨天,当我们将雨伞转动时,伞面边沿的水滴沿着伞的切线方向飞出.实际上物体(看作质点)做曲线运动时,运动方向在不停地变化,其速度方向为质点在其轨迹曲线上的切线方向,我们可以利用导数研究曲线的切线问题.
水滴沿伞边切线飞出
2019年国际田联钻石联赛伦敦站男子200米比赛,中国选手谢震业以19秒88夺冠,这不仅刷新了全国纪录,还创造了新的亚洲纪录.赛后各国教练都在研究他的弯道技术,通过回放录像分析其弯道时的运动方向.这需要求运动曲线在任一点的切线.怎样求曲线的切线?
观察函数f(x)的图象平均变化率
表示什么
O
A
B
x
y
y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
直线AB的斜率
思考
函数平均变化率的几何意义和物理意义
平均变化率的几何意义是表示函数y=f(x)图象上割线P1P2的斜率(其中P1(x1,f(x1)),P2(x2,f(x2))),
问题 抛物线的切线的斜率
P
o
x
y
y=f(x)
割线
切线
T
请看当点 沿着曲线逐渐向点 接近时,割线 绕着点P逐渐转动的情况.
P点无限趋近于P0点时,割线P0P无限趋近于一个确定的位置P0T
o
x
y
y=f(x)
P
割线
切线
T
h
t
o
思考:
导数的概念
解析:
(1)Δy=2(3+Δx)2+4(3+Δx)-(2×32+4×3)
=12Δx+2(Δx)2+4Δx
=2(Δx)2+16Δx,
=2Δx+16.
=16.
=4x0+4,
∴f′(x0)=4x0+4=12,
解得x0=2.
求切点坐标可以按以下步骤进行
(1)设出切点坐标;
(2)利用导数或斜率公式求出斜率;
(3)利用斜率关系列方程,求出切点的横坐标;
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
=2x0+1,
又切线斜率为3即2x0+1=3,
∴x0=1,
则y0=0.
解析:设点M(x0,y0),
y′|x=3=32=9,
即曲线在P(3,9)处的切线的斜率等于9.
由直线的点斜式方程可得,所求切线方程为y-9=9(x-3),
即9x-y-18=0.
导数与函数图象升降的关系
例4 若函数y=f(x)的导函数在区间[a,b]上是增函数,
则函数y=f(x)在区间[a,b]上的图象可能是下图中的 ( )
[解析] 由导数的几何意义知导函数递增说明函数切线斜率随x增大而变大,因此应选A.
导数与函数图象升降的关系
若函数y=f(x)在x=x0处的导数存在且f′(x0)>0(即切线的斜率大于零),则函数y=f(x)在x=x0附近的图象是上升的;
若f′(x0)<0(即切线的斜率小于零),则函数y=f(x)在x=x0附近的图象是下降的.
导数绝对值的大小反映了曲线上升和下降的快慢.
曲线f(x)在x=x0附近的升降情况 切线的
斜率k 切线的
倾斜角
f′(x0)>0 上升 k>0 锐角
f′(x0)<0 下降 k<0 钝角
f′(x0)=0 平坦 k=0 零角(切线与x轴平行)
说明:切线斜率的绝对值的大小反映了曲线在相应点附近上升或下降的快慢.
巩固练习.已知函数y=f(x),y=g(x)的导函数的图象如图,
那么y=f(x),y=g(x)的图象可能是 ( )
从导函数的图象可知两个函数在x0处斜率相同,可以排除B、C.
再者导函数的函数值反映的是原函数的斜率大小,可明显看出y=f(x)的导函数的值在减小,所以原函数的斜率慢慢变小,排除A.
解析:点(5,f(5))在切线y=-x+8上,
∴f(5)=-5+8=3.
且k=f′(5)=-1
∴f(5)+f′(5)=2.
一、导数的概念
1.函数的平均变化率
对于函数y=f(x),设自变量x从x0变化到x0+Δx,相应地,函数值y就从f(x0)变化到f(x0+Δx),这时,x的变化量为Δx,y的变化量为Δy=f(x0+Δx)-f(x0).我们把比值 ,即 =______________________叫做函数y=f(x)从x0到x0+Δx的平均变化率.
y
x
y
x
2.函数在x=x0处的导数
如果当Δx→0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称y=f(x)在x=x0处可导,把这个确定的值叫做y=f(x)在x=x0处的导数(或瞬时变化率),记作f′(x0)或y′|x=x0,
y
x
y
x
对导数概念的再理解
(1)函数应在点x0的附近有定义,否则导数不存在;
(2)导数是一个局部概念,它只与函数y=f(x)在x=x0及其附近的函数值有关,与Δx无关;
(3)导数的实质是一个极限值.
二、导数的几何意义
导数f '(x)表示函数y=f(x)在x=x0处的瞬时变化率,反映了函数y=f(x)在x=x0附近的变化情况.那么导数的几何意义是什么?
平均变化率表示什么?
表示割线PP0的斜率
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
当点P(x,f(x))沿着曲线f(x)无限接近于点P0(x0,f(x0)) ,
割线P0P无限接近于一个确定的位置,
这个确定的位置的直线P0T
称为曲线y=f(x)在点P0处的切线.
割线P0P 的斜率
当 时,k 无限接近函数
y=f(x)在x=x0的导数f '(x0)
导数的几何意义:f '(x)是函数 y=f(x) 在x=x0处切线P0T的斜率.
(1)曲线的切线与割线
①曲线的切线是由割线绕一点转动,当另一点无限接近这一点时割线趋于的直线.
②曲线的切线就是割线趋近于某一确定位置的直线,体现了无限趋近的思想.
(2)曲线的切线与导数
①函数f(x)在x=x0处有导数,则在该点处函数f(x)表示的曲线必有切线,且导数值是该切线的斜率.
②函数f(x)表示的曲线在点(x0,f(x0))处有切线,但函数f(x)在该点处不一定可导,如f(x)= 在x=0处有切线,但不可导.
曲线的切线并不一定与曲线只有一个交点,可以有多个,甚至可以有无穷多个.与曲线只有一个公共点的直线也不一定是曲线的切线.
3
三、导函数
对于函数y=f(x),当x=x0时,f′(x0)是一个确定的数,当x变化时,f′(x)便是一个关于x的函数,我们称它为函数y=f(x)的导函数(简称为导数),即f′(x)=y′=________________.
题型一
求函数在某点处的导数
简称:一差、二比、三极限
题型二
求曲线的切线方程
[例2] (链接教科书第70页练习2题)已知曲线C:y=x3.
(1)求曲线C在横坐标为x=1的点处的切线方程;
(2)求曲线C过点(1,1)的切线方程.
(1)将x=1代入曲线C的方程得y=1,∴切点P(1,1).
∴k=y′|x=1=3.
∴曲线在点P(1,1)处的切线方程为y-1=3(x-1),
即3x-y-2=0.
(2)设切点为Q(x0,y0),由(1)可知y′|x=x0=3x02,由题意可知kPQ=y′|x=x0,
①当x0=1时,切点坐标为(1,1),相应的切线方程为3x-y-2=0.
相应的切线方程为3x-4y+1=0.
求曲线y=x2+1过点P(1,0)的切线方程.
设切点为Q(a,a2+1),
∵在点Q处的切线方程为y-(a2+1)=2a(x-a),*
把点(1,0)代入(*)式得-(a2+1)=2a(1-a).
题型三
导数几何意义的应用
探究1 求切点坐标
例3 已知曲线y=x2+6的切线分别符合下列条件,求切点.
(1)平行于直线y=4x-3;
(2)垂直于直线2x-y+5=0.
设切点坐标为(x0,y0).f′(x)=
∴过(x0,y0)的切线的斜率为2x0.
(1)∵切线与直线y=4x-3平行,∴2x0=4,x0=2,y0=x02+6=10,
即过曲线y=x2+6上点(2,10)的切线与直线y=4x-3平行.
(2)∵切线与直线2x-y+5=0垂直,
∴2x0×2=-1,
即过曲线y=x2+6上点
的切线与直线2x-y+5=0垂直.
探究2 与曲线的切点相关的问题
例4 已知直线l1为曲线y=x2+x-2在(1,0)处的切线,l2为该曲线的另一条切线,且l1⊥l2.
(1)求直线l2的方程;
(2)求由直线l1,l2和x轴围成的三角形面积.
(1)y′=
所以y′|x=1=2×1+1=3,
所以直线l1的方程为y=3(x-1),即y=3x-3.
设直线l2过曲线y=x2+x-2上的点B(b,b2+b-2),
则l2的方程为y=(2b+1)x-b2-2.因为l1⊥l2,
1.如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.
o
x
y
P
5
点(5,f(5))在切线y=-x+8上,
∴f(5)=-5+8=3.
且f′(5)=-1,∴f(5)+f′(5)=2.
2.已知函数y=f(x)的图象如图,则f′(xA)与f′(xB)的大小关系是( )
A.0>f′(xA)>f′(xB) B.f′(xA)
o
x
y
B
A
3.李华在参加一次同学聚会时,用如图所示的圆口杯喝饮料,他想:如果向杯子中倒饮料的速度一定(即单位时间内倒入的饮料量相同),那么杯子中饮料的高度h是关于时间t的函数h(t),则函数h(t)的图象可能是 ( )
o
t
h
o
t
h
o
t
h
o
t
h
h0
h0
h0
h0
t0
t0
t0
t0
由于圆口杯是“下细上粗”,则开始饮料高度增加较快,以后饮料高度增加得越来越慢,仅有B符合.
A
B
C
D
1.导数的定义
如果当Δx→0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称y=f(x)在x=x0处可导,把这个确定的值叫做y=f(x)在x=x0处的导数(或瞬时变化率),记作f′(x0)或y′|x=x0,
y
x
y
x
2.导数的几何意义
曲线y=f(x)在点(x0,y0)的切线斜率为.
知识点1 过关自诊
1.判断正误.(正确的打√,错误的打×)
(4)函数的平均变化率越小,表示函数值变化得越慢.( )
×
优化设计大本
知识点3 过关自诊
1.判断正误.(正确的打√,错误的打×)
(2)直线与曲线相切,则直线与曲线只有一个公共点.( )
×
知识点4 过关自诊
1.判断正误.(正确的打√,错误的打×)
(3)f'(x0)=(f(x0))'.( )
×
探究点二
利用导数的定义求函数的导数
【例2】(1)求函数y=x- 在x=-1处的导数.
(2)求函数y=f(x)=-x2+3x的导数.
分析(1)可以直接利用函数在某一点处的导数的定义求解,也可先求出函数的导函数,再计算导函数在x=-1处的函数值;(2)可按照函数导数的定义分步求解.
探究点四
导数几何意义的应用
角度1求切线方程
【例4】已知曲线C:y=x3.
(1)求曲线C在横坐标为x=1的点处的切线方程;
(2)求曲线C过点P(1,1)的切线方程.
优化设计小本
