5.2.1-5.2.2导数的运算 课件(共45张PPT)
文档属性
| 名称 | 5.2.1-5.2.2导数的运算 课件(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 00:00:00 | ||
图片预览









文档简介
(共45张PPT)
5.2.1 基本初等函数的导数
情境导入
根据导数的定义,求函数 y=f(x) 的导数的三个步骤:
2.算比值:
1.求增量:
3.取极限:
求导数不能每次都求极限,有没有更直接出结果的方法?
如何利用定义求出 y=c ,y=x,y=x2, 的导数?
新课引入
课堂探究
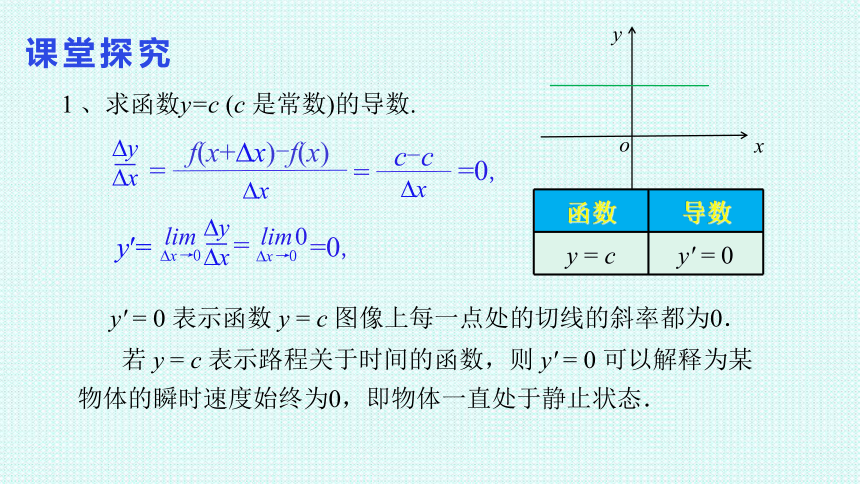
1 、求函数y=c (c 是常数)的导数.
y
x
=
f(x+ x)-f(x)
x
=
c-c
x
=0,
y′=
lim
x→0
y
x
=0,
=
lim
x→0
0
y' = 0 表示函数 y = c 图像上每一点处的切线的斜率都为0.
若 y = c 表示路程关于时间的函数,则 y' = 0 可以解释为某物体的瞬时速度始终为0,即物体一直处于静止状态.
o
x
y
函数 导数
y = c y' = 0
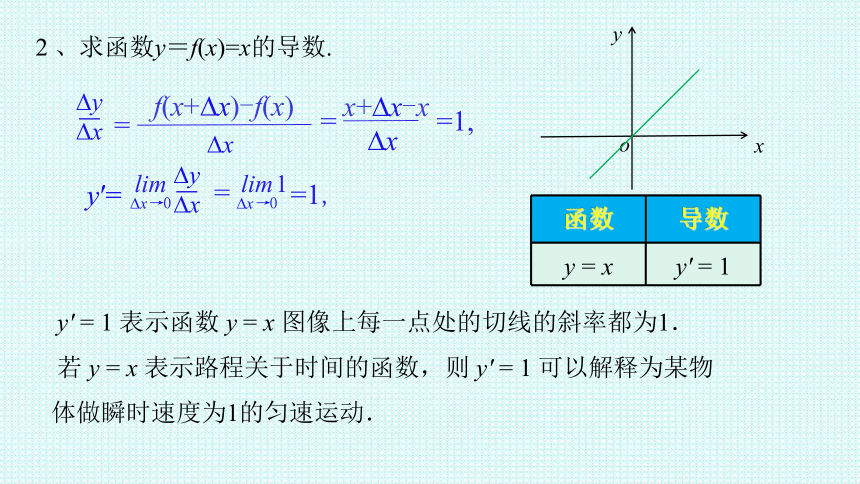
2 、求函数y=f(x)=x的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x-x
=1,
y′=
lim
x→0
y
x
=1,
=
lim
x→0
1
o
x
y
函数 导数
y = x y' = 1
y' = 1 表示函数 y = x 图像上每一点处的切线的斜率都为1.
若 y = x 表示路程关于时间的函数,则 y' = 1 可以解释为某物体做瞬时速度为1的匀速运动.
3、求函数y=f(x)=x2的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)2-x2
=2x+ x,
y′=
lim
x→0
y
x
=2x,
=
lim
x→0
(2x+ x)
函数 导数
y = x2 y' = 2x
o
x
y
y' = 2x 表示函数 y = x2 图像上点(x, y)处的切线的斜率都为2x,说明随着 x 的变化,切线的斜率也在变化.
另一方面,从导数作为函数在一点的瞬时变化率来看,表明:当 x<0时,随着 x 的增加,函数 y = x2 减少得越来越慢;当x>0时,随着 x 的增加,函数 y = x2 增加得越来越快.
4、求函数y=f(x)=x3的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)3-x3
=3x2+3x· x+( x)2,
o
x
y
y′=
lim
x→0
y
x
=3x2,
=
lim
x→0
(3x2+3x· x+( x)2)
函数 导数
y = x3 y' = 3x2
y'=3x2表示函数y=x3的图象上点(x,y)处切线的斜率为3x2,这说明随着x的变化,切线的斜率也在变化,且恒为非负数.
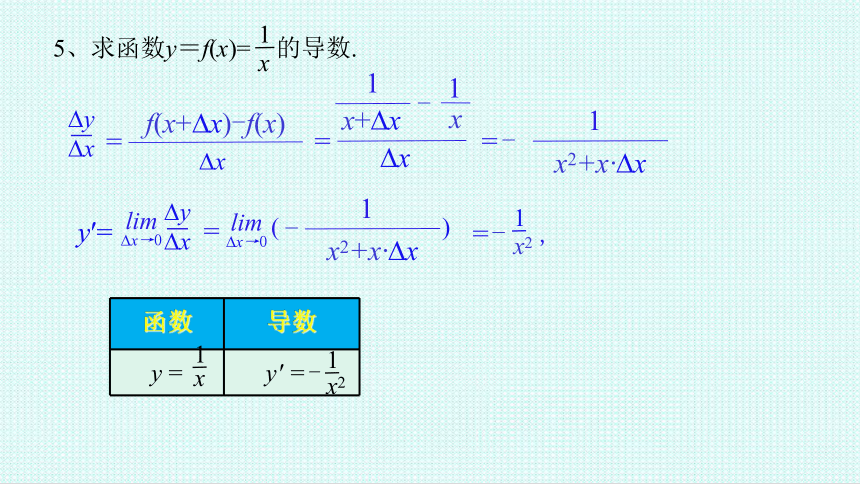
5、求函数y=f(x)= 的导数.
1
x
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x
1
x
1
-
-
x2+x· x
1
=
y′=
lim
x→0
y
x
-
x2+x· x
1
( )
= ,
=
lim
x→0
1
x2
-
函数 导数
y = y' =-
1
x
1
x2
知识梳理
1.几个常用函数的导数
公式形成
思考:以上这些函数均可表示为y=xα(α∈Q*)的形式,其导数有何规律?
思考:还有哪些基本初等函数?它们的导数是什么?
幂函数
指数函数
三角函数
对数函数
基本初等函数的导数公式
原函数 导函数
(1)f(x)=c f′(x)=0
(2)f(x)=xn(n∈Q) f′(x)=n·xn-1
(3)f(x)=sinx f′(x)=cosx
(4)f(x)=cosx f′(x)=-sinx
(5)f(x)=ax f′(x)=axlna
(6)f(x)=ex f′(x)=ex
(7)f(x)=logax f′(x)=
(8)f(x)=lnx f′(x)=
题型一 利用导数公式求函数的导数
例1 求下列函数的导数:
(1)y=sin ;(2)y=5x;(3)y= ;(4)y= ;(5)y=log3x.
π
3
1
x4
(1)y'=0
(2)y'=(5x)′=5xln 5
(5)y′=(log3x)′
= ,
1
xln3
(4)y′=(x )′
3
5
3
5
x
-
2
5
=
已知 f (x) = cosx,g (x) = x,求适合 f ' (x)+g'(x) = 0 的 x 的值
f ' (x)=-sinx,g'(x)=1,
f ' (x)+g'(x) = 0即sinx=1.
表面终边落在y的正半轴
{x|x= +2kπ,k∈Z}
π
2
f′(1)=1,
所以ln a=1,所以a=e.
题型三 导数的综合应用
例3(链接教科书第75页例2)(1)质点的运动方程是S(t)=sin t,则质点在t= 时的速度为________;质点运动的加速度为________;
(2)已知两条曲线y=sin x,y=cos x,是否存在这两条曲线的一个公共点,使在这一点处,两条曲线的切线互相垂直?并说明理由.
(1) v(t)=S′(t)=cos t,
∵v(t)=cos t,
∴加速度a(t)=v′(t)=(cos t)′=-sin t.
(2)由于y=sin x,y=cos x,设这两条曲线的一个公共点为P(x0,y0).∴两条曲线在P(x0,y0)处的斜率分别为k1=cos x0,k2=-sin x0.
若使两条切线互相垂直,必须cos x0·(-sin x0)=-1,
即sin x0·cos x0=1,也就是sin 2x0=2,这是不可能的.
∴两条曲线不存在公共点,使在这一点处的两条切线互相垂直.
由y=ex得y′=ex,曲线在点(0,1)处的斜率k1=e0=1,
设P(m,n),
由题意知k1k2=-1,所以k2=-1,由此易得m=1,n=1,
即点P的坐标为(1,1),k2=-1.所以点P处的切线方程为x+y-2=0.
设曲线 y=xn+1(n∈N*) 在点(1, 1)处的切线与 x 轴的交点的横坐标为xn,令an=lg xn,则 a1+a2+…+a99 的值为________.
∵y=xn+1,∴y′=(n+1)xn,y′ | x=1=n+1.
∴曲线在点(1, 1)处的切线方程为 y-1=(n+1)(x-1).
令y=0,
xn=
n+1
n
故an=lg n-lg (n+1).
∴a1 + a2 +…+ a99=(lg 1-lg 2)+(lg 2-lg 3)+…+(lg 98-lg 99)+(lg 99-lg 100)=lg 1-lg 100=-2.
5.2.2 导数的四则运算法则
回顾旧知
基本初等函数的导数公式
探究一:两个函数的和(差)的导数
探究新知
导数的运算法则1:
例题精讲
教材76页
解:
探究二:两个函数的积(商)的导数
探究新知
导数的运算法则2:
导数的运算法则3:
导数的四则运算法则
f(x),g(x)是可导的.
法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:
[f(x)±g(x)]′=f′(x)±g′(x)
求y=x3+sinx的导数.
y′=3x2+cosx
求y=x4-x2-x+3的导数.
y′=4x3-2x-1
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)
推论:常数与函数的积的导数,等于常数乘函数的导数,即:
法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
=
求函数y= 的导数.
1
x
y′=
x2
0-1
=-
1
x2
求函数y=tanx的导数.
y′=(tanx)′
sinx
cosx
=( )′
cos2x
=
cos2x+sin2x
cos2x
=
1
求函数y= 的导数.
x+1
x-1
y′=( )′=
x+1
x-1
(x+1)2
x+1-(x-1)
(x+1)2
2
=
应用导数公式的注意事项
(1)两个导数的和差运算只可推广到有限个函数的和差的导数运算,即[u(x)±v(x)±…±w(x)]′=u′(x)±v′(x)±…±w′(x);
(2)两个函数可导,则它们的和、差、积、商(商的分母不为零)必可导.同上可推广到有限个函数的函数乘积的导数即:①[af(x)+bg(x)]′=af′(x)+bg′(x);②[u(x)v(x)…w(x)]′=u′(x)v(x)…w(x)+u(x)v′(x)…w(x)+…+u(x)v(x)…w′(x);
(3)若两个函数不可导,则它们的和、差、积、商不一定不可导;
(4)对于较复杂的函数式,应先进行适当的化简变形,化为较简单的函数式后再求导,可简化求导过程.
题型一 利用导数的四则运算法则求导
(1)y′=2x-2x-3.
(2)y′=(ln 3+1)·(3e)x-2xln 2.
题型二 导数几何意义的综合应用
例2(链接教科书第78页练习3题)(1)曲线y=
的切线的斜率为 ( )
(1)y′=
(2)设曲线y=xln x在点(x0,y0)处的切线与直线x-y-2=0平行.
∵y′=ln x+1,∴y′|x=x0=ln x0+1=1,解得x0=1,
∴y0=0,即切点坐标为(1,0).∴切点(1,0)到直线x-y-2=0的距离为
即曲线y=xln x上的点到直线x-y-2=0
1.此类问题往往涉及切点、切点处的导数、切线方程三个主要元素,其他的条件可以进行转化,从而转化为这三个要素间的关系.
2.准确利用求导法则求出导函数是解决此类问题的第一步,也是解题的关键,务必做到准确.
3.分清已知点是否在曲线上,若不在曲线上,则要设出切点,这是解题时的易错点.
通性通法
∴切线方程为y=2(x-1),即2x-y-2=0.
令x=0得y=-2;令y=0得x=1.
在点(1,0)处
的切线与坐标轴围成的面积为
题型三 利用函数的导数求参数
例3(1)(2019·全国卷Ⅲ)已知曲线y=aex+xln x在点(1,ae)处的切线方程为y=2x+b,则 ( )
A.a=e,b=-1 B.a=e,b=1
C.a=e-1,b=1 D.a=e-1,b=-1
(1)y′=aex+ln x+1,k=y′|x=1=ae+1,∴ 切线方程为
y-ae=(ae+1)(x-1),即y=(ae+1)x-1.
又∵ 切线方程为y=2x+b,
即a=e-1,b=-1
(2)已知函数f(x)=ax3+bx2+cx的图象过点(1,5),其导函数
y=f′(x)的图象如图所示,则函数f(x)的解析式为________.
o
x
y
1
2
(2)∵f′(x)=3ax2+2bx+c,f′(1)=0,f′(2)=0,f(1)=5,
故函数f(x)的解析式是f(x)=2x3-9x2+12x.
(2021·黑龙江鹤岗市第一中学高二期末)已知f(x)=x2+2xf′(1),
则f′(0)=________.
因为f(x)=x2+2xf′(1),所以f′(x)=2x+2f′(1).令x=1,得f′(1)=2×1+2f′(1),解得f′(1)=-2,所以f′(x)=2x-4,所以f′(0)=2×0-4=-4.
的切线与直线x+ay+1=0垂直,
则a=________.
a=1.
探究点三
导数公式与运算法则的综合应用
角度1 解析式中含f'(a)的导数问题
【例3】 (2021陕西延安黄陵中学高三期中)已知函数f(x)的导函数是f'(x),且满足f(x)=2xf'(1)+ln ,则f(1)=( )
A.-e B.2 C.-2 D.e
答案 B
解析 因为f(x)=2xf'(1)+ln =2xf'(1)-ln x,所以f'(x)=2f'(1)- .
所以f'(1)=2f'(1)-1,解得f'(1)=1.
所以f(x)=2x+ln ,f(1)=2+ln 1=2.故选B.
优化设计大本
变式训练 2(2021武汉外国语学校高二期末)已知f(x)=x2-xf'(0)-1,则f(2)的值为( )
A.1 B.-1 C.3 D.-3
答案 C
解析 ∵f(x)=x2-xf'(0)-1,∴f'(x)=2x-f'(0),∴f'(0)=-f'(0),∴f'(0)=0.∴f(x)=x2-1,
因此f(2)=22-1=3.
角度2 利用导数公式及函数性质解题
【例4】已知f1(x)=sin x+cos x,fn+1(x)是fn(x)的导函数,即f2(x)=f'1(x),f3(x)=f'2(x),…,fn+1(x)=f'n(x),n∈N*,则f2 021(x)=( )
A.sin x+cos x B.sin x-cos x C.-sin x+cos x D.-sin x-cos x
答案 A
解析 因为f1(x)=sin x+cos x,
所以f2(x)=f'1(x)=cos x-sin x,
f3(x)=f'2(x)=-sin x-cos x,f4(x)=f'3(x)=-cos x+sin x,f5(x)=f'4(x)=sin x+cos x,……,可知fn(x)的解析式周期为4.因为2 021=505×4+1,
所以f2 021(x)=f1(x)=sin x+cos x,故选A.
角度3用待定系数法处理求导问题
【例5】 设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f'(x)=2x+1.求y=f(x)的函数表达式.
解 ∵f'(x)=2x+1,
∴f(x)=x2+x+c(c为常数).
又方程f(x)=0有两个相等的实根,即x2+x+c=0有两个相等的实根,
∴Δ=12-4c=0,即c= ,
∴f(x)=x2+x+ .
变式训练3
已知f'(x)是一次函数,关于x的方程x2·f'(x)-(2x-1)·f(x)=1对一切x∈R恒成立,求f(x)的解析式.
解 由f'(x)为一次函数可知f(x)为二次函数,设f(x)=ax2+bx+c(a≠0),则f'(x)=2ax+b,则原方程可化为x2(2ax+b)-(2x-1)·(ax2+bx+c)=1,即(a-b)x2+(b-2c)x+c-1=0,
又该方程对一切x∈R恒成立,
变式训练4
已知函数 ,且f(x)的图象在x=1处与直线y=2相切.
(1)求函数f(x)的解析式;
(2)若P(x0,y0)为f(x)图象上的任意一点,直线l与f(x)的图象切于点P,求直线l的斜率k的取值范围.
优化设计小本
5.2.1 基本初等函数的导数
情境导入
根据导数的定义,求函数 y=f(x) 的导数的三个步骤:
2.算比值:
1.求增量:
3.取极限:
求导数不能每次都求极限,有没有更直接出结果的方法?
如何利用定义求出 y=c ,y=x,y=x2, 的导数?
新课引入
课堂探究
1 、求函数y=c (c 是常数)的导数.
y
x
=
f(x+ x)-f(x)
x
=
c-c
x
=0,
y′=
lim
x→0
y
x
=0,
=
lim
x→0
0
y' = 0 表示函数 y = c 图像上每一点处的切线的斜率都为0.
若 y = c 表示路程关于时间的函数,则 y' = 0 可以解释为某物体的瞬时速度始终为0,即物体一直处于静止状态.
o
x
y
函数 导数
y = c y' = 0
2 、求函数y=f(x)=x的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x-x
=1,
y′=
lim
x→0
y
x
=1,
=
lim
x→0
1
o
x
y
函数 导数
y = x y' = 1
y' = 1 表示函数 y = x 图像上每一点处的切线的斜率都为1.
若 y = x 表示路程关于时间的函数,则 y' = 1 可以解释为某物体做瞬时速度为1的匀速运动.
3、求函数y=f(x)=x2的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)2-x2
=2x+ x,
y′=
lim
x→0
y
x
=2x,
=
lim
x→0
(2x+ x)
函数 导数
y = x2 y' = 2x
o
x
y
y' = 2x 表示函数 y = x2 图像上点(x, y)处的切线的斜率都为2x,说明随着 x 的变化,切线的斜率也在变化.
另一方面,从导数作为函数在一点的瞬时变化率来看,表明:当 x<0时,随着 x 的增加,函数 y = x2 减少得越来越慢;当x>0时,随着 x 的增加,函数 y = x2 增加得越来越快.
4、求函数y=f(x)=x3的导数.
y
x
=
f(x+ x)-f(x)
x
=
x
(x+ x)3-x3
=3x2+3x· x+( x)2,
o
x
y
y′=
lim
x→0
y
x
=3x2,
=
lim
x→0
(3x2+3x· x+( x)2)
函数 导数
y = x3 y' = 3x2
y'=3x2表示函数y=x3的图象上点(x,y)处切线的斜率为3x2,这说明随着x的变化,切线的斜率也在变化,且恒为非负数.
5、求函数y=f(x)= 的导数.
1
x
y
x
=
f(x+ x)-f(x)
x
=
x
x+ x
1
x
1
-
-
x2+x· x
1
=
y′=
lim
x→0
y
x
-
x2+x· x
1
( )
= ,
=
lim
x→0
1
x2
-
函数 导数
y = y' =-
1
x
1
x2
知识梳理
1.几个常用函数的导数
公式形成
思考:以上这些函数均可表示为y=xα(α∈Q*)的形式,其导数有何规律?
思考:还有哪些基本初等函数?它们的导数是什么?
幂函数
指数函数
三角函数
对数函数
基本初等函数的导数公式
原函数 导函数
(1)f(x)=c f′(x)=0
(2)f(x)=xn(n∈Q) f′(x)=n·xn-1
(3)f(x)=sinx f′(x)=cosx
(4)f(x)=cosx f′(x)=-sinx
(5)f(x)=ax f′(x)=axlna
(6)f(x)=ex f′(x)=ex
(7)f(x)=logax f′(x)=
(8)f(x)=lnx f′(x)=
题型一 利用导数公式求函数的导数
例1 求下列函数的导数:
(1)y=sin ;(2)y=5x;(3)y= ;(4)y= ;(5)y=log3x.
π
3
1
x4
(1)y'=0
(2)y'=(5x)′=5xln 5
(5)y′=(log3x)′
= ,
1
xln3
(4)y′=(x )′
3
5
3
5
x
-
2
5
=
已知 f (x) = cosx,g (x) = x,求适合 f ' (x)+g'(x) = 0 的 x 的值
f ' (x)=-sinx,g'(x)=1,
f ' (x)+g'(x) = 0即sinx=1.
表面终边落在y的正半轴
{x|x= +2kπ,k∈Z}
π
2
f′(1)=1,
所以ln a=1,所以a=e.
题型三 导数的综合应用
例3(链接教科书第75页例2)(1)质点的运动方程是S(t)=sin t,则质点在t= 时的速度为________;质点运动的加速度为________;
(2)已知两条曲线y=sin x,y=cos x,是否存在这两条曲线的一个公共点,使在这一点处,两条曲线的切线互相垂直?并说明理由.
(1) v(t)=S′(t)=cos t,
∵v(t)=cos t,
∴加速度a(t)=v′(t)=(cos t)′=-sin t.
(2)由于y=sin x,y=cos x,设这两条曲线的一个公共点为P(x0,y0).∴两条曲线在P(x0,y0)处的斜率分别为k1=cos x0,k2=-sin x0.
若使两条切线互相垂直,必须cos x0·(-sin x0)=-1,
即sin x0·cos x0=1,也就是sin 2x0=2,这是不可能的.
∴两条曲线不存在公共点,使在这一点处的两条切线互相垂直.
由y=ex得y′=ex,曲线在点(0,1)处的斜率k1=e0=1,
设P(m,n),
由题意知k1k2=-1,所以k2=-1,由此易得m=1,n=1,
即点P的坐标为(1,1),k2=-1.所以点P处的切线方程为x+y-2=0.
设曲线 y=xn+1(n∈N*) 在点(1, 1)处的切线与 x 轴的交点的横坐标为xn,令an=lg xn,则 a1+a2+…+a99 的值为________.
∵y=xn+1,∴y′=(n+1)xn,y′ | x=1=n+1.
∴曲线在点(1, 1)处的切线方程为 y-1=(n+1)(x-1).
令y=0,
xn=
n+1
n
故an=lg n-lg (n+1).
∴a1 + a2 +…+ a99=(lg 1-lg 2)+(lg 2-lg 3)+…+(lg 98-lg 99)+(lg 99-lg 100)=lg 1-lg 100=-2.
5.2.2 导数的四则运算法则
回顾旧知
基本初等函数的导数公式
探究一:两个函数的和(差)的导数
探究新知
导数的运算法则1:
例题精讲
教材76页
解:
探究二:两个函数的积(商)的导数
探究新知
导数的运算法则2:
导数的运算法则3:
导数的四则运算法则
f(x),g(x)是可导的.
法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:
[f(x)±g(x)]′=f′(x)±g′(x)
求y=x3+sinx的导数.
y′=3x2+cosx
求y=x4-x2-x+3的导数.
y′=4x3-2x-1
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)
推论:常数与函数的积的导数,等于常数乘函数的导数,即:
法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
=
求函数y= 的导数.
1
x
y′=
x2
0-1
=-
1
x2
求函数y=tanx的导数.
y′=(tanx)′
sinx
cosx
=( )′
cos2x
=
cos2x+sin2x
cos2x
=
1
求函数y= 的导数.
x+1
x-1
y′=( )′=
x+1
x-1
(x+1)2
x+1-(x-1)
(x+1)2
2
=
应用导数公式的注意事项
(1)两个导数的和差运算只可推广到有限个函数的和差的导数运算,即[u(x)±v(x)±…±w(x)]′=u′(x)±v′(x)±…±w′(x);
(2)两个函数可导,则它们的和、差、积、商(商的分母不为零)必可导.同上可推广到有限个函数的函数乘积的导数即:①[af(x)+bg(x)]′=af′(x)+bg′(x);②[u(x)v(x)…w(x)]′=u′(x)v(x)…w(x)+u(x)v′(x)…w(x)+…+u(x)v(x)…w′(x);
(3)若两个函数不可导,则它们的和、差、积、商不一定不可导;
(4)对于较复杂的函数式,应先进行适当的化简变形,化为较简单的函数式后再求导,可简化求导过程.
题型一 利用导数的四则运算法则求导
(1)y′=2x-2x-3.
(2)y′=(ln 3+1)·(3e)x-2xln 2.
题型二 导数几何意义的综合应用
例2(链接教科书第78页练习3题)(1)曲线y=
的切线的斜率为 ( )
(1)y′=
(2)设曲线y=xln x在点(x0,y0)处的切线与直线x-y-2=0平行.
∵y′=ln x+1,∴y′|x=x0=ln x0+1=1,解得x0=1,
∴y0=0,即切点坐标为(1,0).∴切点(1,0)到直线x-y-2=0的距离为
即曲线y=xln x上的点到直线x-y-2=0
1.此类问题往往涉及切点、切点处的导数、切线方程三个主要元素,其他的条件可以进行转化,从而转化为这三个要素间的关系.
2.准确利用求导法则求出导函数是解决此类问题的第一步,也是解题的关键,务必做到准确.
3.分清已知点是否在曲线上,若不在曲线上,则要设出切点,这是解题时的易错点.
通性通法
∴切线方程为y=2(x-1),即2x-y-2=0.
令x=0得y=-2;令y=0得x=1.
在点(1,0)处
的切线与坐标轴围成的面积为
题型三 利用函数的导数求参数
例3(1)(2019·全国卷Ⅲ)已知曲线y=aex+xln x在点(1,ae)处的切线方程为y=2x+b,则 ( )
A.a=e,b=-1 B.a=e,b=1
C.a=e-1,b=1 D.a=e-1,b=-1
(1)y′=aex+ln x+1,k=y′|x=1=ae+1,∴ 切线方程为
y-ae=(ae+1)(x-1),即y=(ae+1)x-1.
又∵ 切线方程为y=2x+b,
即a=e-1,b=-1
(2)已知函数f(x)=ax3+bx2+cx的图象过点(1,5),其导函数
y=f′(x)的图象如图所示,则函数f(x)的解析式为________.
o
x
y
1
2
(2)∵f′(x)=3ax2+2bx+c,f′(1)=0,f′(2)=0,f(1)=5,
故函数f(x)的解析式是f(x)=2x3-9x2+12x.
(2021·黑龙江鹤岗市第一中学高二期末)已知f(x)=x2+2xf′(1),
则f′(0)=________.
因为f(x)=x2+2xf′(1),所以f′(x)=2x+2f′(1).令x=1,得f′(1)=2×1+2f′(1),解得f′(1)=-2,所以f′(x)=2x-4,所以f′(0)=2×0-4=-4.
的切线与直线x+ay+1=0垂直,
则a=________.
a=1.
探究点三
导数公式与运算法则的综合应用
角度1 解析式中含f'(a)的导数问题
【例3】 (2021陕西延安黄陵中学高三期中)已知函数f(x)的导函数是f'(x),且满足f(x)=2xf'(1)+ln ,则f(1)=( )
A.-e B.2 C.-2 D.e
答案 B
解析 因为f(x)=2xf'(1)+ln =2xf'(1)-ln x,所以f'(x)=2f'(1)- .
所以f'(1)=2f'(1)-1,解得f'(1)=1.
所以f(x)=2x+ln ,f(1)=2+ln 1=2.故选B.
优化设计大本
变式训练 2(2021武汉外国语学校高二期末)已知f(x)=x2-xf'(0)-1,则f(2)的值为( )
A.1 B.-1 C.3 D.-3
答案 C
解析 ∵f(x)=x2-xf'(0)-1,∴f'(x)=2x-f'(0),∴f'(0)=-f'(0),∴f'(0)=0.∴f(x)=x2-1,
因此f(2)=22-1=3.
角度2 利用导数公式及函数性质解题
【例4】已知f1(x)=sin x+cos x,fn+1(x)是fn(x)的导函数,即f2(x)=f'1(x),f3(x)=f'2(x),…,fn+1(x)=f'n(x),n∈N*,则f2 021(x)=( )
A.sin x+cos x B.sin x-cos x C.-sin x+cos x D.-sin x-cos x
答案 A
解析 因为f1(x)=sin x+cos x,
所以f2(x)=f'1(x)=cos x-sin x,
f3(x)=f'2(x)=-sin x-cos x,f4(x)=f'3(x)=-cos x+sin x,f5(x)=f'4(x)=sin x+cos x,……,可知fn(x)的解析式周期为4.因为2 021=505×4+1,
所以f2 021(x)=f1(x)=sin x+cos x,故选A.
角度3用待定系数法处理求导问题
【例5】 设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f'(x)=2x+1.求y=f(x)的函数表达式.
解 ∵f'(x)=2x+1,
∴f(x)=x2+x+c(c为常数).
又方程f(x)=0有两个相等的实根,即x2+x+c=0有两个相等的实根,
∴Δ=12-4c=0,即c= ,
∴f(x)=x2+x+ .
变式训练3
已知f'(x)是一次函数,关于x的方程x2·f'(x)-(2x-1)·f(x)=1对一切x∈R恒成立,求f(x)的解析式.
解 由f'(x)为一次函数可知f(x)为二次函数,设f(x)=ax2+bx+c(a≠0),则f'(x)=2ax+b,则原方程可化为x2(2ax+b)-(2x-1)·(ax2+bx+c)=1,即(a-b)x2+(b-2c)x+c-1=0,
又该方程对一切x∈R恒成立,
变式训练4
已知函数 ,且f(x)的图象在x=1处与直线y=2相切.
(1)求函数f(x)的解析式;
(2)若P(x0,y0)为f(x)图象上的任意一点,直线l与f(x)的图象切于点P,求直线l的斜率k的取值范围.
优化设计小本
