5.3.2.2函数的最大(小)值 课件(共37张PPT)
文档属性
| 名称 | 5.3.2.2函数的最大(小)值 课件(共37张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 11:02:25 | ||
图片预览









文档简介
(共37张PPT)
5.3.2.2 函数的最大(小)值
复习回顾
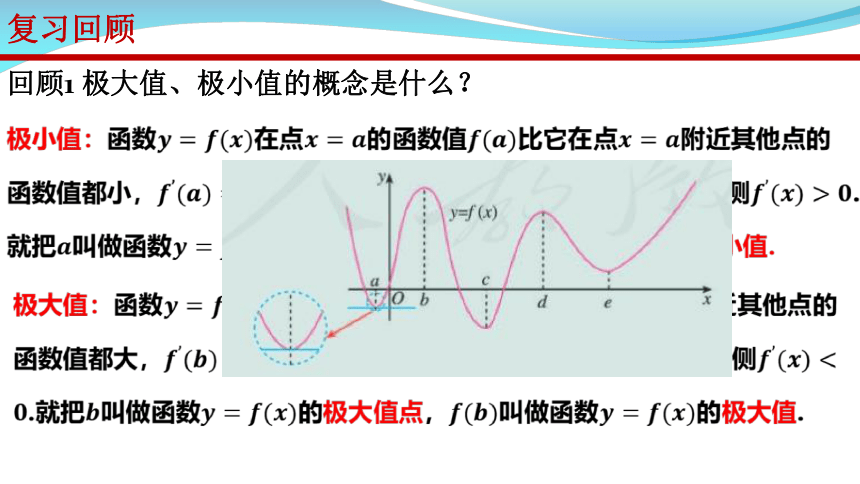
回顾1 极大值、极小值的概念是什么?
复习回顾
回顾2 如何求函数的极值?
新课导入
思考1:如图是函数 , 的图象,你能找出它的极大值、极小值吗?进一步地,你能找出函数 在区间 上的最大值、最小值吗?
a
x1
x2
x3
x4
x5
x6
b
x
y
O
函数的最值
观察图象,我们发现,
, , 是函数的极小值, , ,
是函数的极大值.
进一步地,函数 在区间 上的最小值是 ,最大值是 .
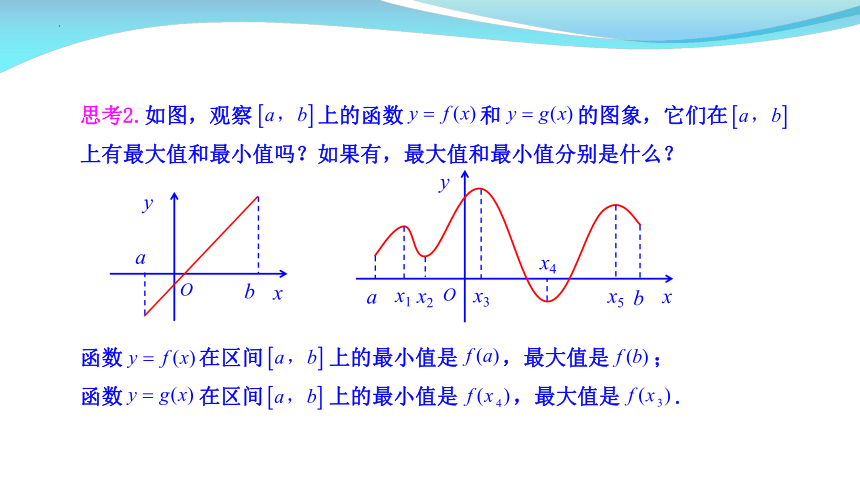
思考2.如图,观察 上的函数 和 的图象,它们在 上有最大值和最小值吗?如果有,最大值和最小值分别是什么?
a
b
x
y
O
a
b
x
y
O
x1
x2
x3
x4
x5
函数 在区间 上的最小值是 ,最大值是 ;
函数 在区间 上的最小值是 ,最大值是 .
一般地,如果在区间[a,b]上函数y=f (x)的图象是一条连续不断的曲线,那么它必有最大值与最小值.
函数最值的理解
(1)函数的最值是一个整体性的概念.函数极值是在局部上对函数值的比较,具有相对性;而函数的最值则是表示函数在整个定义域上的情况,是对整个区间上的函数值的比较.
(2)函数在一个闭区间上若存在最大值或最小值,则最大值或最小值只能各有一个,具有唯一性,而极大值和极小值可能多于一个,也可能没有,例如:常数函数就既没有极大值也没有极小值.
知识梳理
三.新课探究
函数最值
一般地,对于函数f(x),给定区间I,
若对任意x∈I,存在x0∈I,使得f(x)≥f(x0),则称f(x0)为函数f(x)在区间I上的最小值;
若对任意x∈I,存在x0∈I,使得f(x)≤f(x0),则称f(x0)为函数f(x)在区间I上的最大值.
求函数在闭区间上的最值
求函数 f(x)在闭区间[a,b]上的最值的步骤:
1.求函数 在(a,b)内的极值;
2.将函数 的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个就是最大值,最小的一个就是最小值.
例6
解:
x 0 (0, 2) 2 (2, 3) 3
f′(x)
f(x)
x
y
O
4
2
3
求f(x)在[a,b]上的最大值与最小值的步骤如下:
(2) 将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
方法归纳
(1) f(x)在(a,b)内导函数为零的点,并计算出其函数值;
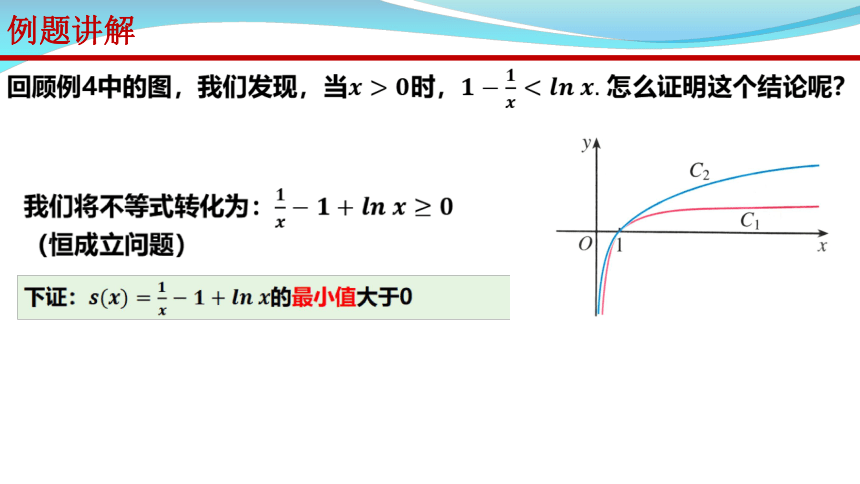
例题讲解
新知讲解
1.利用导数解决与函数相关的问题:
例7
解:
例7
解:
x
y
O
1
-1
-2
例7
解:
x
y
O
1
-1
-2
由例7可见,函数f(x)的图象直观地反映了函数f(x)的性质. 通常,可以按如下步骤画出函数f(x)的大致图象:
(1) 求出函数f(x)的定义域;
(2) 求导数f′(x)及函数f′(x)的零点;
(3) 用f′(x)的零点将f(x)的定义域划分为若干个区间,列表给出f′(x)在各区间上的正负,并得出f(x)的单调性与极值;
(4) 确定f(x)的图象所经过的一些特殊点,以及图象的变化趋势;
(5) 画出f(x)的大致图象.
问题 饮料瓶大小对饮料公司利润的影响
(1)你是否注意过,市场上等量的小包装的物品一般比大包装的要贵些?你想从数学上知道它的道理吗?
(2)是不是饮料瓶越大,饮料公司的利润越大?
(1)瓶子半径多大时,能使每瓶饮料的利润最大?
(2)瓶子半径多大时,每瓶饮料的利润最小?
解:
由题意可知,每瓶饮料的利润是
因此,
如果我们不用导数工具,直接从函数 f(r)的图象(右图)上观察,你有什么发现?
从图象上容易看出,当 r=3时,f(3)=0,即瓶子的半径是3 cm时,饮料的利润与饮料瓶的成本恰好相等;当 r>3时,利润才为正值.
答:(1)半径为6 cm时,利润最大.
(2)半径为2 cm时,利润最小,这时f(2)<0,表示此种瓶内饮料的利润还不够瓶子的成本,此时利润是负值.
2.[含参的函数最值问题]已知a∈R,函数f(x)=x2(x-a).求函数y=f(x)在区间[1,2]上的最小值.
课堂小结
课堂小结
课堂小结
注:
(3)极值只能在区间内取得,最值则可以在端点处取得.有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值不在端点处取得时必定是极值.
角度2 求函数在开区间或无穷区间上的最大(小)值
【例2】求下列函数的最大值与最小值:
分析没有给定相应的闭区间,因此应分析函数在其定义域上的单调性与极值情况,根据单调性与极值画出函数的大致图象,结合图象求出最大值与最小值.
优化设计大本
(2)函数的定义域是R,且f'(x)=2x·ex+(x2-3)ex=ex(x2+2x-3),令f'(x)>0,得x>1或x<-3;令f'(x)<0,得-3内单调递减,因此函数f(x)在x=-3处取得极大值,极大值f(-3)=6e-3;
在x=1处取得极小值,极小值f(1)=-2e.
又由f(x)>0,得x> 或x<- ;由f(x)<0得,-角度2 与函数最大(小)值和参数有关的综合问题
【例4】设函数f(x)=tx2+2t2x+t-1(x∈R,t>0).
(1)求f(x)的最小值h(t);
(2)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
分析(1)利用配方法,即可求出二次函数f(x)的最小值h(t);(2)构造函数g(t)=h(t)-(-2t+m),只需使g(t)在(0,2)上的最大值小于零即可求得m的取值范围.
解 (1)∵f(x)=t(x+t)2-t3+t-1(x∈R,t>0),∴当x=-t时,f(x)取最小值,
即f(-t)=-t3+t-1,即h(t)=-t3+t-1.
(2)令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g'(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).当t变化时,g'(t),g(t)的变化情况如下表:
∴g(t)在(0,2)内有极大值也是最大值g(1)=1-m.
h(t)<-2t+m在(0,2)内恒成立等价于g(t)<0在(0,2)内恒成立,即等价于
1-m<0.∴m的取值范围为(1,+∞).
t (0,1) 1 (1,2)
g'(t) + 0 -
g(t) 单调递增 极大值1-m 单调递减
规律方法 分离参数求解不等式恒成立问题的步骤
变式探究 1若将本例(2)的条件改为“存在t∈[0,2],使h(t)<-2t+m成立”,则实数m的取值范围如何求解
解 令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g'(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).当t变化时,g'(t),g(t)的变化情况如下表:
∴g(t)在[0,2]上有最小值g(2)=-3-m,
存在t∈[0,2],使h(t)<-2t+m成立,
等价于g(t)的最小值g(2)<0.
∴-3-m<0,∴m>-3,故实数m的取值范围为(-3,+∞).
t 0 (0,1) 1 (1,2) 2
g'(t) + 0 -
g(t) -1-m 单调递增 极大值1-m 单调递减 -3-m
变式探究 2若将本例(2)的条件改为“对任意的t1,t2∈[0,2],都有h(t1)<-2t2+m”,求实数m的取值范围.
优化设计小本
5.3.2.2 函数的最大(小)值
复习回顾
回顾1 极大值、极小值的概念是什么?
复习回顾
回顾2 如何求函数的极值?
新课导入
思考1:如图是函数 , 的图象,你能找出它的极大值、极小值吗?进一步地,你能找出函数 在区间 上的最大值、最小值吗?
a
x1
x2
x3
x4
x5
x6
b
x
y
O
函数的最值
观察图象,我们发现,
, , 是函数的极小值, , ,
是函数的极大值.
进一步地,函数 在区间 上的最小值是 ,最大值是 .
思考2.如图,观察 上的函数 和 的图象,它们在 上有最大值和最小值吗?如果有,最大值和最小值分别是什么?
a
b
x
y
O
a
b
x
y
O
x1
x2
x3
x4
x5
函数 在区间 上的最小值是 ,最大值是 ;
函数 在区间 上的最小值是 ,最大值是 .
一般地,如果在区间[a,b]上函数y=f (x)的图象是一条连续不断的曲线,那么它必有最大值与最小值.
函数最值的理解
(1)函数的最值是一个整体性的概念.函数极值是在局部上对函数值的比较,具有相对性;而函数的最值则是表示函数在整个定义域上的情况,是对整个区间上的函数值的比较.
(2)函数在一个闭区间上若存在最大值或最小值,则最大值或最小值只能各有一个,具有唯一性,而极大值和极小值可能多于一个,也可能没有,例如:常数函数就既没有极大值也没有极小值.
知识梳理
三.新课探究
函数最值
一般地,对于函数f(x),给定区间I,
若对任意x∈I,存在x0∈I,使得f(x)≥f(x0),则称f(x0)为函数f(x)在区间I上的最小值;
若对任意x∈I,存在x0∈I,使得f(x)≤f(x0),则称f(x0)为函数f(x)在区间I上的最大值.
求函数在闭区间上的最值
求函数 f(x)在闭区间[a,b]上的最值的步骤:
1.求函数 在(a,b)内的极值;
2.将函数 的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个就是最大值,最小的一个就是最小值.
例6
解:
x 0 (0, 2) 2 (2, 3) 3
f′(x)
f(x)
x
y
O
4
2
3
求f(x)在[a,b]上的最大值与最小值的步骤如下:
(2) 将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
方法归纳
(1) f(x)在(a,b)内导函数为零的点,并计算出其函数值;
例题讲解
新知讲解
1.利用导数解决与函数相关的问题:
例7
解:
例7
解:
x
y
O
1
-1
-2
例7
解:
x
y
O
1
-1
-2
由例7可见,函数f(x)的图象直观地反映了函数f(x)的性质. 通常,可以按如下步骤画出函数f(x)的大致图象:
(1) 求出函数f(x)的定义域;
(2) 求导数f′(x)及函数f′(x)的零点;
(3) 用f′(x)的零点将f(x)的定义域划分为若干个区间,列表给出f′(x)在各区间上的正负,并得出f(x)的单调性与极值;
(4) 确定f(x)的图象所经过的一些特殊点,以及图象的变化趋势;
(5) 画出f(x)的大致图象.
问题 饮料瓶大小对饮料公司利润的影响
(1)你是否注意过,市场上等量的小包装的物品一般比大包装的要贵些?你想从数学上知道它的道理吗?
(2)是不是饮料瓶越大,饮料公司的利润越大?
(1)瓶子半径多大时,能使每瓶饮料的利润最大?
(2)瓶子半径多大时,每瓶饮料的利润最小?
解:
由题意可知,每瓶饮料的利润是
因此,
如果我们不用导数工具,直接从函数 f(r)的图象(右图)上观察,你有什么发现?
从图象上容易看出,当 r=3时,f(3)=0,即瓶子的半径是3 cm时,饮料的利润与饮料瓶的成本恰好相等;当 r>3时,利润才为正值.
答:(1)半径为6 cm时,利润最大.
(2)半径为2 cm时,利润最小,这时f(2)<0,表示此种瓶内饮料的利润还不够瓶子的成本,此时利润是负值.
2.[含参的函数最值问题]已知a∈R,函数f(x)=x2(x-a).求函数y=f(x)在区间[1,2]上的最小值.
课堂小结
课堂小结
课堂小结
注:
(3)极值只能在区间内取得,最值则可以在端点处取得.有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值不在端点处取得时必定是极值.
角度2 求函数在开区间或无穷区间上的最大(小)值
【例2】求下列函数的最大值与最小值:
分析没有给定相应的闭区间,因此应分析函数在其定义域上的单调性与极值情况,根据单调性与极值画出函数的大致图象,结合图象求出最大值与最小值.
优化设计大本
(2)函数的定义域是R,且f'(x)=2x·ex+(x2-3)ex=ex(x2+2x-3),令f'(x)>0,得x>1或x<-3;令f'(x)<0,得-3
在x=1处取得极小值,极小值f(1)=-2e.
又由f(x)>0,得x> 或x<- ;由f(x)<0得,-
【例4】设函数f(x)=tx2+2t2x+t-1(x∈R,t>0).
(1)求f(x)的最小值h(t);
(2)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
分析(1)利用配方法,即可求出二次函数f(x)的最小值h(t);(2)构造函数g(t)=h(t)-(-2t+m),只需使g(t)在(0,2)上的最大值小于零即可求得m的取值范围.
解 (1)∵f(x)=t(x+t)2-t3+t-1(x∈R,t>0),∴当x=-t时,f(x)取最小值,
即f(-t)=-t3+t-1,即h(t)=-t3+t-1.
(2)令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g'(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).当t变化时,g'(t),g(t)的变化情况如下表:
∴g(t)在(0,2)内有极大值也是最大值g(1)=1-m.
h(t)<-2t+m在(0,2)内恒成立等价于g(t)<0在(0,2)内恒成立,即等价于
1-m<0.∴m的取值范围为(1,+∞).
t (0,1) 1 (1,2)
g'(t) + 0 -
g(t) 单调递增 极大值1-m 单调递减
规律方法 分离参数求解不等式恒成立问题的步骤
变式探究 1若将本例(2)的条件改为“存在t∈[0,2],使h(t)<-2t+m成立”,则实数m的取值范围如何求解
解 令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g'(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).当t变化时,g'(t),g(t)的变化情况如下表:
∴g(t)在[0,2]上有最小值g(2)=-3-m,
存在t∈[0,2],使h(t)<-2t+m成立,
等价于g(t)的最小值g(2)<0.
∴-3-m<0,∴m>-3,故实数m的取值范围为(-3,+∞).
t 0 (0,1) 1 (1,2) 2
g'(t) + 0 -
g(t) -1-m 单调递增 极大值1-m 单调递减 -3-m
变式探究 2若将本例(2)的条件改为“对任意的t1,t2∈[0,2],都有h(t1)<-2t2+m”,求实数m的取值范围.
优化设计小本
