2023年中考数学复习 第四讲与三角形相关的二次函数存在性问题专题(压轴题专题讲义)(含解析)
文档属性
| 名称 | 2023年中考数学复习 第四讲与三角形相关的二次函数存在性问题专题(压轴题专题讲义)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 901.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 00:00:00 | ||
图片预览




文档简介
第四讲 与三角形相关的二次函数存在性问题(压轴题专题讲义)
内容提要
(一)关于等腰三角形找点(作点)和求点的不同
(二)关于直角三角形找点和求点的方法
知识点拓展详解
(一)关于等腰三角形找点(作点)和求点的不同,
1、等腰三角形找点(作点)方法:以已知边为边长,作等腰三角形,运用两园一线法,在图上找出存在点的个数,只找不求。
2、等腰三角形求点方法:以已知边为边长,在抛物线或坐标轴或对称轴上找点,与已知点构成等腰三角形,先设所求点的坐标,然后根据两点间的距离公式求出三点间的线段长度,然后分顶点进行讨论,
(二)关于直角三角形找点和求点的方法
1、直角三角形找点(作点)方法:以已知边为边长,作直角三角形,运用两线一园法,在图上找出存在点的个数,只找不求。所谓的两线就是指以已知边为直角边,过已知边的两个端点分别作垂线与抛物线或坐标轴或对称轴的交点,就是所求的点;一圆就是以已知边为直径,以已知边的中点作圆,与抛物线或坐标轴或对称轴的交点即为所求的点。
2、具体方法
(1)121k k ;(2)三角形全等(注意寻找特殊角,如30°、60°、45°、90°)
(3)三角形相似;经常利用一线三等角模型
(4)勾股定理;
当题目中出现了特殊角时,优先考虑全等法
最新典型例题——教你解题
例题1.如图,抛物线y=x2﹣x﹣的图象与x轴交于点A,B,与y轴交于点C,顶点为D,以AB为直径在x轴上方画半圆交y轴于点E,圆心为I,P是半圆上一动点,连接DP,点Q为PD的中点.下列四种说法:①点C在⊙I上;②IQ⊥PD;③当点P沿半圆从点B运动至点A时,点Q运动的路径长为π;④线段BQ的长可以是3.2.
其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
【思路点拨】由抛物线y=x2﹣x﹣得A(﹣1,0),B(3,0),C(0,﹣),可得I(1,0),顶点D(1,﹣2),
①根据勾股定理求出IC,即可求解;
②根据垂径定理即可求解;
③点P的运动轨迹为以I为圆心的半圆,则点Q的运动轨迹为以R为圆心的半圆,即可求解;
④根据勾股定理即可求解.
【归纳总结】将函数知识与方程、几何知识有机地结合在一起.这类试题一般难度较大.解这类问题关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.
最新典型例题2.
如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc<0;③a+b≥am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【思路点拨】根据已知点的特点可求对称轴为直线x=1,则b=﹣2a;由函数的图象可知,a<0,c>0,再由b=﹣2a可知b>0;当x=1时,函数有最大值a+b+c;再由铅锤法求△BCQ的面积,从而确定当m=2时,三角形面积有最大值.
提高同步练习
一.选择题
1.如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点,抛物线的顶点为D,点C为AB的中点,以C为圆心,AC长为半径在x轴的上方作一个半圆,点E为半圆上一动点,连接DE,取DE的中点F,当点E沿着半圆从点A运动至点B的过程中,线段AF的最小值为( )
A. B. C. D.
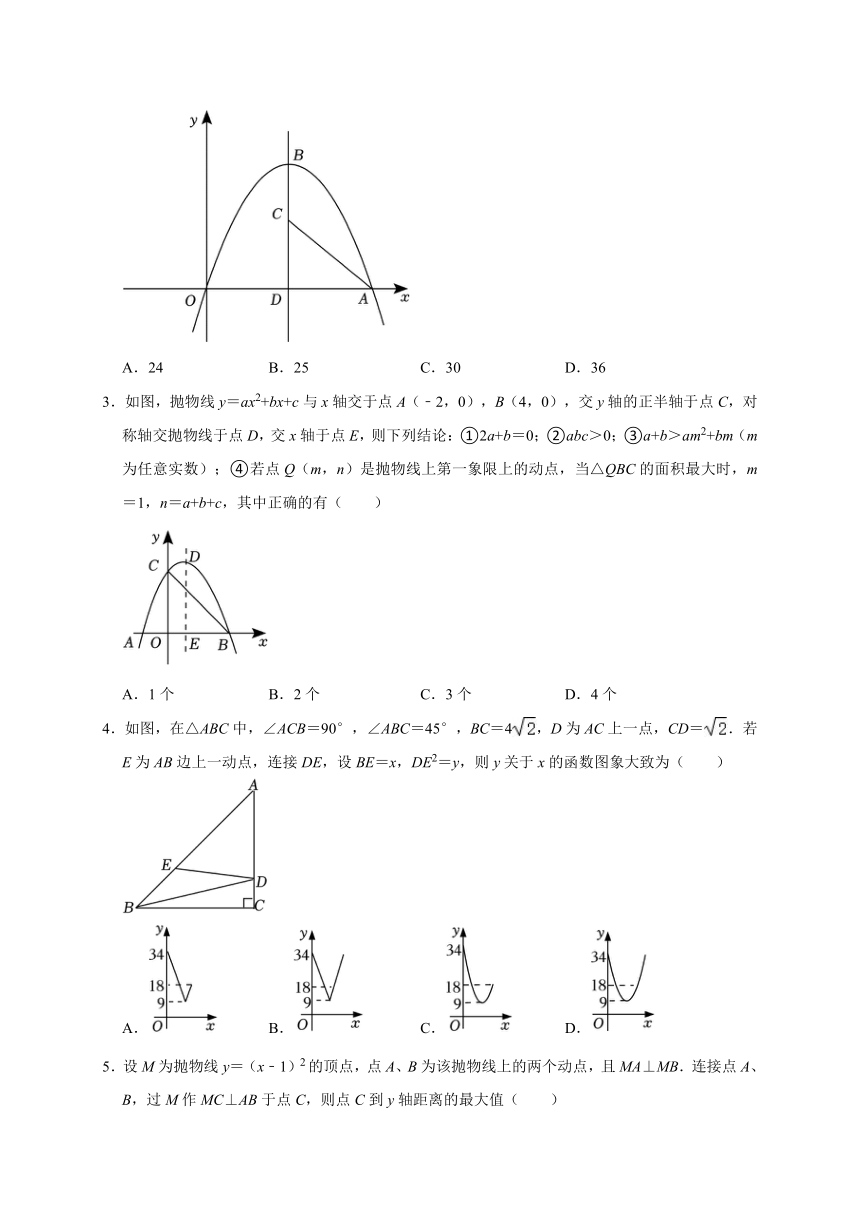
2.如图,在平面直角坐标系中,抛物线y=与x轴的正半轴交于点A,B点为抛物线的顶点,C点为该抛物线对称轴上一点,则3BC+5AC的最小值为( )
A.24 B.25 C.30 D.36
3.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc>0;③a+b>am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=1,n=a+b+c,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,在△ABC中,∠ACB=90°,∠ABC=45°,BC=4,D为AC上一点,CD=.若E为AB边上一动点,连接DE,设BE=x,DE2=y,则y关于x的函数图象大致为( )
A. B. C. D.
5.设M为抛物线y=(x﹣1)2的顶点,点A、B为该抛物线上的两个动点,且MA⊥MB.连接点A、B,过M作MC⊥AB于点C,则点C到y轴距离的最大值( )
A. B. C. D.2
二.填空题(共4小题)
6.在平面直角坐标系中,抛物线y=x2﹣bx+c(b>0,b、c为常数)的顶点为A,与y轴交于点B,点B关于抛物线对称轴的对称点为C.若△ABC是等腰直角三角形,则BC的长为 .
7.如图,已知二次函数y=﹣x2+(a+1)x﹣a的图象与x轴交于A、B两点(点A位于点B的左侧),与y轴交于点C.已知△BAC的面积是6,若在抛物线上存在一点P(与点C不重合),使S△ABP=S△ABC,则点P的坐标为 .
8.如图,在平面直角坐标系中,点 A、点B均在抛物线y=x2上,且AB∥x轴,点 C、点D为线段AB的三等分点,以CD为边向下作矩形CDEF,矩形CDEF的顶点 E、F均在此抛物线上,若矩形CDEF的面积为2,则AB的长为 .
9.抛物线交x轴负半轴于点A,点B是抛物线上一动点,且点B在第二象限,以AB为边,作等腰直角三角形ABP.其中∠ABP=90°,当点P恰好在y轴上时,点P的坐标为 .
三.解答题(共3小题)
10.抛物线线L:y=ax2+bx+c(a≠0)与直线l:y=kx+m(k≠0)有且只有一个交点,我们就称此直线l与抛物线L的相切.直线l叫做抛物线L的切线,交点叫做抛物线L的切点.
(1)若点A为抛物线y=x2﹣2x+4与y轴的交点,求以点A为切点的该抛物线的切线的解析式;
(2)已知一次函数y1=2x,二次函数y2=x2+1,是否存在二次函数y3=ax2+bx+c,其图象经过点(﹣3,2),使得直线y1=2x与y2=x2+1,y3=ax2+bx+c都相切于同一点?若存在,求出y3的解析式;若不存在,请说明理由;
(3)已知直线l1:y=k1x+m1(k1≠0)、直线l2:y2=k2x+m2(k2≠0)是抛物线y=﹣x2+2x+3的两条切线,当l1与l2的交点P的纵坐标为5时,试判断k1 k2是否为定值,并说明理由.
11.如图,抛物线y=ax2+bx+3与x轴相交于A、B两点,与y轴相交于点C,已知B点的坐标为(6,0),抛物线的对称轴为直线x=2,点D是BC上方抛物线上的一个动点.
(1)求这个抛物线的解析式;
(2)当△BCD的面积为时,求点D的坐标;
(3)是否存在点D,使得∠DCB=2∠ABC?若存在,请求出点D的坐标;若不存在,请说明理由.
12.如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A'B'O.
(1)有一条抛物线经过点A',B',B,求该抛物线的解析式.
(2)设该抛物线的一个动点P的横坐标为t.
①当0<t<2时,求四边形ABPB'的面积S与t的函数关系式,并求出S的最大值;
②点Q是直线AB上的一个动点,若以AB'为边,点A,B',Q,P为顶点的四边形是平行四边形,请求出所有符合条件的t的值.
参考答案与试题解析
【教你解题】
最新典型例题1:如图,抛物线y=x2﹣x﹣的图象与x轴交于点A,B,与y轴交于点C,顶点为D,以AB为直径在x轴上方画半圆交y轴于点E,圆心为I,P是半圆上一动点,连接DP,点Q为PD的中点.下列四种说法:
①点C在⊙I上;
②IQ⊥PD;
③当点P沿半圆从点B运动至点A时,点Q运动的路径长为π;
④线段BQ的长可以是3.2.
其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
解:抛物线y=x2﹣x﹣的图象与坐标轴交于点A,B,C,
∴A(﹣1,0),B(3,0),C(0,﹣),
∴点I(1,0),⊙I的半径为2,
∵y=x2﹣x﹣=(x﹣1)2﹣2,
∴顶点D的坐标为:(1,﹣2),
∴ID=2,
∴点D在⊙I上.
①IC===≠2,故点C不在⊙I上,故①不正确;
②∵圆心为I,P是半圆上一动点,点D在⊙I上,点Q为PD的中点.
∴IQ⊥PD,故②正确;
③图中实点G、Q、I、F是点N运动中所处的位置,
则GF是等腰直角三角形的中位线,GF=AB=2,ID交GF于点R,则四边形GDFI为正方形,
当点P在半圆任意位置时,中点为Q,连接IQ,则IQ⊥PD,连接QR,
则QR=ID=IR=RD=RG=RF=GF=1,则点Q的运动轨迹为以R为圆心的半圆,
则Q运动的路径长=×2πr=π,故③正确;
④由③得,当点Q运动到点G的位置时,BQ的长最大,
最大值为=<3.2,
∴线段BQ的长不可以是3.2,故④不正确.
故正确说法有:②③.
故选:B.
最新典型例题2.如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc<0;③a+b≥am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
解:∵抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),B(4,0),
∴对称轴为直线x==1,
∴﹣=1,
∴2a=﹣b,
∴2a+b=0,故①正确,符合题意;
∵抛物线开口向下,
∴a<0,
∴b=﹣2a>0,
∵抛物线交y轴的正半轴,
∴c>0,
∴abc<0,故②正确,符合题意;
∵抛物线的对称轴x=1,开口向下,
∴x=1时,y有最大值,最大值=a+b+c.
∴a+b+c≥am2+bm+c(m为任意实数),
∴a+b≥am2+bm(m为任意实数),故③正确,符合题意;
④∵C(0,c),
设直线BC的解析式为y=kx+t,
∴,
解得,
∴y=﹣x+c,
将点A(﹣2,0)代入y=ax2﹣2ax+c,
∴c=﹣8a.
∴y=ax2﹣2ax﹣8a.
过点Q作QN∥y轴交BC于点P,
∵Q(m,n),
∴P(m,2am﹣8a),
∴PQ=n﹣2am+8a.
∴S△QBC=×4×(n﹣2am+8a)=2(n﹣2am+8a),
∵n=am2﹣2am﹣8a,
∴S△QBC=2(am2﹣4am)=2a(m﹣2)2﹣8a.
∴当m=2时,△QBC的面积最大,
故④正确,符合题意;
故选:D.
提高同步练习
一.选择题
1.如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点,抛物线的顶点为D,点C为AB的中点,以C为圆心,AC长为半径在x轴的上方作一个半圆,点E为半圆上一动点,连接DE,取DE的中点F,当点E沿着半圆从点A运动至点B的过程中,线段AF的最小值为( )
A. B. C. D.
【分析】由题意可知E点在以C为圆心,2为半径的半圆上,则F点在以G(1,﹣2)为圆心,1为半径的半圆上,AF的最小值为AG﹣1,求出AG即可求解.
解:连接AD、AE,
令y=0,则x2﹣2x﹣3=0,
解得x=3或x=﹣1,
∴A(﹣1,0),B(3,0),
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点D(1,﹣4),
∴AD的中点为H(0,﹣2),
连接HF,
∵F是DE的中点,
∴HF∥AE,HF=AE,
∵AB=4,C(2,0),
∴E点在以C为圆心,2为半径的半圆上,
∴F点在以G(1,﹣2)为圆心,1为半径的半圆上,
∴AG=2,
∴AF的最小值为2﹣1,
故选:C.
2.如图,在平面直角坐标系中,抛物线y=与x轴的正半轴交于点A,B点为抛物线的顶点,C点为该抛物线对称轴上一点,则3BC+5AC的最小值为( )
A.24 B.25 C.30 D.36
【分析】连接OB,过C点作CM⊥OB于M点,过A点作AN⊥OB于N点,抛物线的对称轴与x轴交于点D,先求出抛物线与坐标轴的交点坐标,继而得出BD、OA、OD,再证明△OBD∽△CBM,△OBD∽△OAN,进而可得3BC+5AC=5MC+5AC=5(AC+CM),当A、C、M三点共线,且三点连线垂直OB时,AC+CM最小,根据求出AN,AC+CM最小值即为AN,则问题得解.
解:连接OB,过C点作CM⊥OB于M点,过A点作AN⊥OB于N点,抛物线的对称轴与x轴交于点D,如图,
令y=0,得方程,
解得:x1=0,x2=6,
∴A点坐标为(6,0),即OA=6,
将配成顶点式得:,
∴B点坐标为(3,4),
∴BD=4,OD=3,
∵CM⊥OB,AN⊥OB,
∴∠BMC=∠ANO=90°,
根据抛物线对称轴的性质可知BD⊥OA,
∴∠BDO=90°,
在Rt△BDO中,
利用勾股定理得,
∵∠OBD=∠CBM,∠BDO=∠BMC=90°,
∴△OBD∽△CBM,
同理可证得△OBD∽△OAN,
∴,,
∴,即3BC=5MC,
∴3BC+5AC=5MC+5AC=5(AC+CM),
∵当A、C、M三点共线,且三点连线垂直OB时,AC+CM最小,
∴AC+CM最小值为AN,如图所示,
∵,
∴,
∴AC+CM最小值,
∴即3BC+5AC=5(AC+CM)=24.
故选:A.
3.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc>0;③a+b>am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=1,n=a+b+c,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据已知点的特点可求对称轴为直线x=1,则b=﹣2a;由函数的图象可知,a<0,c>0,再由b=﹣2a可知b>0;当x=1时,函数有最大值a+b+c;再由铅锤法求△BCQ的面积,从而确定当m=2时,三角形面积有最大值.
解:∵抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),B(4,0),
∴对称轴为直线x==1,
∴﹣=1,
∴2a=﹣b,
∴2a+b=0,故①正确,符合题意;
∵抛物线开口向下,
∴a<0,
∴b=﹣2a>0,
∵抛物线交y轴的正半轴,
∴c>0,
∴abc<0,故②错误,不符合题意;
∵抛物线的对称轴x=1,开口向下,
∴x=1时,y有最大值,最大值=a+b+c,
∴a+b+c≥am2+bm+c(m为任意实数),
∴a+b≥am2+bm(m为任意实数),故③错误,不符合题意;
④∵C(0,c),
设直线BC的解析式为y=kx+t,
∴,
解得,
∴y=﹣x+c,
将点A(﹣2,0)代入y=ax2﹣2ax+c,
∴c=﹣8a,
∴y=ax2﹣2ax﹣8a,
过点Q作QN∥y轴交BC于点P,
∵Q(m,n),
∴P(m,2am﹣8a),
∴PQ=n﹣2am+8a,
∴S△QBC=4×(n﹣2am+8a)=2(n﹣2am+8a),
∵n=am2﹣2am﹣8a,
∴S△QBC=2(am2﹣4am)=2a(m﹣2)2﹣8a,
∴当m=2时,△QBC的面积最大,
故④不正确,不符合题意;
故选:A.
4.如图,在△ABC中,∠ACB=90°,∠ABC=45°,BC=4,D为AC上一点,CD=.若E为AB边上一动点,连接DE,设BE=x,DE2=y,则y关于x的函数图象大致为( )
A. B. C. D.
【分析】过点D作DF⊥AB于点F,利用等腰直角三角形的性质求得线段AF,DF,AB的长度,利用含x的代数式表示出EF,再利用勾股定理即可求得y与x的函数解析式,利用二次函数的性质结合自变量x的取值范围即可得出结论.
解:过点D作DF⊥AB于点F,如图,
∵∠ACB=90°,∠ABC=45°,BC=4,
∴AB==8,∠A=45°,
∵DF⊥AB,
∴AF=DF=AD,
∵AC=BC=4,CD=,
∴AD=3,
∴AF=DF=3.
∴BF=AB﹣AF=5,
∵BE=x,
∴当点E在点F的下方时,EE=5﹣x,
当点E在点F的上方时,EF=x﹣5,
∵DE2=EF2+DF2,
∴y=(5﹣x)2+32=x2﹣10x+34(0≤x≤5)或y=(x﹣5)2+32=x2﹣10x+34(5<x≤8),
∴当0≤x≤5时,y有最大值为34,最小值为9,
当5<x≤8时,y有最大值为34,此时x=8,
又∵y=(5﹣x)2+32=x2﹣10x+34(0≤x≤5)或y=(x﹣5)2+32=x2﹣10x+34(5<x≤8)的图象为抛物线的一部分,
故选:C.
5.设M为抛物线y=(x﹣1)2的顶点,点A、B为该抛物线上的两个动点,且MA⊥MB.连接点A、B,过M作MC⊥AB于点C,则点C到y轴距离的最大值( )
A. B. C. D.2
【分析】如图,以M为原点建立新坐标系.过点B作BE⊥x轴于点E,过点A作AD⊥x轴于点D,AH⊥BE于点H,交y′轴于点G,设AB交y′轴于点K.首先证明直线AB经过定点K(0,1),判断出点C的运动轨迹,可得结论.
解:如图,以M为原点建立新坐标系.过点B作BE⊥x轴于点E,过点A作AD⊥x轴于点D,AH⊥BE于点H,交y′轴于点G,设AB交y′轴于点K.
则抛物线在新坐标系下的解析式y′=x2,顶点M(0,0).
设MD=a,ME=b,K(0,m),则AD=a2,BE=b2,
∵KG∥BH,
∴=,
∴=,
∴m=ab,
∵AM⊥MB,
∴∠AMB=∠ADM=∠BEM=90°,
∴∠AMD+∠BME=90°,∠BME+∠EBM=90°,
∴∠AMD=∠MBE,
∴△ADM∽△MEB,
∴=,
∴=,
∴ab=1,
∴m=1,
∴K(0,1),
∴MK=1,
∵AC⊥AB,
∴∠MCK=90°,
∴点C的运动轨迹是以MK为直径的圆,
∴当点C在y′的右边侧,到y′轴的距离为时,点C到y轴的距离最大,最大值为1+=.
故选:B.
二.填空题(共4小题)
6.在平面直角坐标系中,抛物线y=x2﹣bx+c(b>0,b、c为常数)的顶点为A,与y轴交于点B,点B关于抛物线对称轴的对称点为C.若△ABC是等腰直角三角形,则BC的长为 8 .
【分析】分别求出A(2b,c﹣b2),B(0,c),C(4b,c),再由等腰直角三角形斜边的中线等于斜边的一半,建立方程4b=2(c﹣c+b2),求出b的值即可求解.
解:∵y=x2﹣bx+c=(x﹣2b)2+c﹣b2,
∴顶点A(2b,c﹣b2),对称轴为直线x=2b,
当x=0时,y=c,
∴B(0,c),
∵点B关于抛物线对称轴的对称点为C,
∴C(4b,c),
∵△ABC是等腰直角三角形,
∴4b=2(c﹣c+b2),
解得b=0或b=2,
∵b>0,
∴b=2,
∴BC=8,
故答案为:8.
7.如图,已知二次函数y=﹣x2+(a+1)x﹣a的图象与x轴交于A、B两点(点A位于点B的左侧),与y轴交于点C.已知△BAC的面积是6,若在抛物线上存在一点P(与点C不重合),使S△ABP=S△ABC,则点P的坐标为 (﹣2,3)或(﹣1+,﹣3)或(﹣1﹣,﹣3) .
【分析】由y=﹣x2+(a+1)x﹣a,令y=0,即﹣x2+(a+1)x﹣a=0,可求出A、B坐标结合三角形的面积,解出a=﹣3;然后根据题意P的纵坐标为±3,分别代入解析式即可求得横坐标,从而求得P的坐标.
解:∵y=﹣x2+(a+1)x﹣a,
令x=0,则y=﹣a,
∴C(0,﹣a),
令y=0,即﹣x2+(a+1)x﹣a=0,
解得x1=a,x2=1,
由图象知:a<0,
∴A(a,0),B(1,0),
∵S△ABC=6,
∴(1﹣a)(﹣a)=6,
解得:a=﹣3,(a=4舍去);
∵a=﹣3,
∴y=﹣x2﹣2x+3,C(0,3),
∵S△ABP=S△ABC.
∴P点的纵坐标为±3,
把y=3代入y=﹣x2﹣2x+3得﹣x2﹣2x+3=3,解得x=﹣2或x=0(与点C重合,舍去);
把y=﹣3代入y=﹣x2﹣2x+3得﹣x2﹣2x+3=﹣3,解得x=﹣1+或x=﹣1﹣,
∴P点的坐标为(﹣2,3)或(﹣1+,﹣3)或(﹣1﹣,﹣3).
故答案为:(﹣2,3)或(﹣1+,﹣3)或(﹣1﹣,﹣3).
8.如图,在平面直角坐标系中,点 A、点B均在抛物线y=x2上,且AB∥x轴,点 C、点D为线段AB的三等分点,以CD为边向下作矩形CDEF,矩形CDEF的顶点 E、F均在此抛物线上,若矩形CDEF的面积为2,则AB的长为 3 .
【分析】设A(a,a2),则B(﹣a,a2),利用抛物线的对称性和点的坐标的特征得到AB=2a,点 A、点B到x轴的距离为a2,利用矩形的性质得到点 C、点D关于y轴对称,HD=HC=a,则E(﹣a,),F(a,),利用矩形的面积公式可得到关于a的方程,利用立方根的意义即可求得a值,则结论可求.
解:抛物线y=x2的对称轴为y轴,
∵点 A、点B均在抛物线y=x2上,且AB∥x轴,
∴点 A、点B关于y轴对称,
设A(a,a2),则B(﹣a,a2),a>0.
∴AB=2a,点 A、点B到x轴的距离为a2.
∵点 C、点D为线段AB的三等分点,
∴CD=a.
设CD与y轴交于点H,
由题意,点 C、点D关于y轴对称,
∴HD=HC=a,
∵矩形CDEF的顶点 E、F均在此抛物线上,
∴E(﹣a,),F(a,),
∵EF∥x轴,
∴点 E、F到x轴的距离为2,
∵AB∥x轴,
∴DE=CF=,
∵矩形CDEF的面积为2,
∴CD CF=2,
∴a =2,
∴,
∴a=.
∴AB=2a=3.
故答案为:3.
9.抛物线交x轴负半轴于点A,点B是抛物线上一动点,且点B在第二象限,以AB为边,作等腰直角三角形ABP.其中∠ABP=90°,当点P恰好在y轴上时,点P的坐标为 (0,1) .
【分析】如图,过点A作AC⊥x轴,过点B作CD⊥y轴于点D,交AC于点C,可证△ABC≌△BPD(AAS),AC=BD,BC=PD,设B(t,﹣t2﹣t+2),可得BD=﹣t,BC=t﹣(﹣3)=t+3,AC=﹣t2﹣t+2,D(0,﹣t2﹣t+2),建立方程求解即可得出答案.
解:如图,过点A作AC⊥x轴,过点B作CD⊥y轴于点D,交AC于点C,
则∠ACB=∠BDP=90°,
∴∠ABC+∠BAC=90°,
∵∠ABP=90°,
∴∠ABC+∠PBD=90°,
∴∠BAC=∠PBD,
∵△ABP是等腰直角三角形,
∴AB=BP,
∴△ABC≌△BPD(AAS),
∴AC=BD,BC=PD,
∵y=﹣x2﹣x+2,
当y=0时,﹣x2﹣x+2=0,
解得:x1=﹣3,x2=1,
∴A(﹣3,0),
设B(t,﹣t2﹣t+2),
则BD=﹣t,BC=t﹣(﹣3)=t+3,AC=﹣t2﹣t+2,D(0,﹣t2﹣t+2),
∴﹣t2﹣t+2=﹣t,
解得:t=﹣2或,
∵点B在第二象限,
∴t=﹣2,
∴B(﹣2,2),D(0,2),BC=DP=1,
∴P(0,1);
故答案为:(0,1).
三.解答题(共3小题)
10.抛物线线L:y=ax2+bx+c(a≠0)与直线l:y=kx+m(k≠0)有且只有一个交点,我们就称此直线l与抛物线L的相切.直线l叫做抛物线L的切线,交点叫做抛物线L的切点.
(1)若点A为抛物线y=x2﹣2x+4与y轴的交点,求以点A为切点的该抛物线的切线的解析式;
(2)已知一次函数y1=2x,二次函数y2=x2+1,是否存在二次函数y3=ax2+bx+c,其图象经过点(﹣3,2),使得直线y1=2x与y2=x2+1,y3=ax2+bx+c都相切于同一点?若存在,求出y3的解析式;若不存在,请说明理由;
(3)已知直线l1:y=k1x+m1(k1≠0)、直线l2:y2=k2x+m2(k2≠0)是抛物线y=﹣x2+2x+3的两条切线,当l1与l2的交点P的纵坐标为5时,试判断k1 k2是否为定值,并说明理由.
【分析】(1)联立得x2﹣(k+2)x=0,根据“抛物线的切点”的定义即可求解;
(2)联立得x2﹣2x+1=0,可得切点为(1,2),根据直线y1=2x与y2=x2+1,y3=ax2+bx+c都相切于同一点,可得经过点(﹣3,2),(1,2),利用待定系数法得,联立得ax2+(2a﹣2)x+2﹣3a=0,由Δ=(2a﹣2)2﹣4a(2﹣3a)=4a2+4﹣8a﹣8a+12a2=16a2﹣16a+4=(4a﹣2)2=0,可得,b=1,,即可得y3的解折式为;
(3)由l1与l2的交点P的纵坐标为5,令P(t,5),则直线l1:y=k1x﹣k1t+5、直线l2:y2=k2x﹣k2t+5,根据“抛物线的切点”的定义得k12+(4t﹣4)k1﹣4=0,,即k1,k2为x2+(4t﹣4)x﹣4=0的两根,由根与系数的关系可得k1 k2=﹣4.
解:(1)∵点A为抛物线y=x2﹣2x+4与y轴的交点,A为切点,
∴A(0,4),
设过点A的切线的解析式为y=kx+4,
联立,
整理得x2﹣(k+2)x=0,
解得x1=0,x2=k+2,
由“抛物线的切点”的定义得,
∴k+2=0,
∴k=﹣2,
∴以点A为切点的该抛物线的切线的解析式为y=﹣2x+4;
(2)∵直线y1=2x与相切,
联立,
整理得x2﹣2x+1=0,
解得x=1,
∴切点为(1,2),
又∵直线y1=2x与y2=x2+1,y3=ax2+bx+c都相切于同一点,
∴经过点(﹣3,2),(1,2),
∴,解得,
∴,
联立,
整理得ax2+(2a﹣2)x+2﹣3a=0,
∴Δ=(2a﹣2)2﹣4a(2﹣3a)=4a2+4﹣8a﹣8a+12a2=16a2﹣16a+4=(4a﹣2)2=0,
∴,b=1,,
∴y3的解折式为;
(3)k1 k2是定值,k1 k2=﹣4,理由如下:
∵l1与l2的交点P的纵坐标为5,
令P(t,5),
∴直线l1:y=k1x+m1=k1t+m1=5、直线l2:y2=k2x+m2=k2t+m2=5,
∴m1=5﹣k1t、直线l2:m2=5﹣k2t,
∴直线l1:y=k1x﹣k1t+5、直线l2:y2=k2x﹣k2t+5,
联立得x2+(k1﹣2)x﹣k1t+2=0,
由抛物线L的切线得:,
同理可得,
∴k1,k2为x2+(4t﹣4)x﹣4=0的两根,
∴k1 k2=﹣4.
11.如图,抛物线y=ax2+bx+3与x轴相交于A、B两点,与y轴相交于点C,已知B点的坐标为(6,0),抛物线的对称轴为直线x=2,点D是BC上方抛物线上的一个动点.
(1)求这个抛物线的解析式;
(2)当△BCD的面积为时,求点D的坐标;
(3)是否存在点D,使得∠DCB=2∠ABC?若存在,请求出点D的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法列方程组求解抛物线的解析式即可;
(2)如图,连接OD,设D(x,﹣x2+x+3),令x=0,则y=3,即C(0,3),而B(6,0),再分别表示S△BOC,S△DOC,S△BOD,再利用△BCD的面积为列方程求解即可;
(3)过D作DQ∥y轴交BC于Q,过C作CF⊥DQ于F,点D作DE⊥BC,垂足为点E,则CF∥x轴,可得∠FCB=∠ABC,证明CD=CQ,DF=FQ,设D(x,﹣x2+x+3),则Q(x,﹣x+3),F(x,3),再列方程求解即可.
解:(1)∵B点的坐标为(6,0),抛物线y=ax2+bx+3的对称轴为直线x=2,
∴,
解得:,
所以抛物线的解析式为y=﹣x2+x+3;
(2)连接OD,过点D作DE⊥OB于点E,如图,
设D(x,﹣x2+x+3),
∵点D是BC上方抛物线上的一个动点,
∴0<x<6.
∴DE=﹣x2+x+3,OE=x,
令x=0,则y=3,
∴C(0,3),
∴OC=3.
∵B(6,0),
∴OB=6.
∵S△BCD=S△DCO+S△DOB﹣S△OBC,△BCD的面积为,
∴×OC OE+×OB DE﹣×OB OC=,
∴×3×x+×6×(﹣x2+x+3)﹣×6×3=,
整理得:x2﹣6x+5=0.
解得:x=1或x=5,
∴D(1,)或(5,);
(3)存在点D,使得∠DCB=2∠ABC,理由:
过D作DQ∥y轴交BC于Q,交OB于点G,过C作CF⊥DQ于F,点D作DE⊥BC,垂足为点E,如图,
当∠DCB=2∠ABC时,
∵CF∥x轴,
∴∠FCB=∠ABC,
∴∠DCB=2∠FCB,
∴∠DCF=∠BCF,
在△DCF和△QCF中,
,
∴△DCF≌△QCF(ASA).
∴CD=CQ,DF=FQ,
设BC的解析式为:y=mx+n,
∴,
解得:,
∴直线BC的解析式y=﹣x+3
设D(x,﹣x2+x+3),
∵点D是BC上方抛物线上的一个动点,
∴0<x<6.
∴DG=﹣x2+x+3,OG=x,
则Q(x,﹣x+3),F(x,3),
∴FG=3,QG=﹣x+3.
∴DF=DG﹣FG=(﹣x2+x+3)﹣3=﹣x2+x,
FQ=FG﹣QG=3﹣(﹣x+3)=x,
∴﹣x2+x=x,
解得:x1=2,x2=0(不符合题意,舍去),
∴x=2.
∴D(2,4).
12.如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A'B'O.
(1)有一条抛物线经过点A',B',B,求该抛物线的解析式.
(2)设该抛物线的一个动点P的横坐标为t.
①当0<t<2时,求四边形ABPB'的面积S与t的函数关系式,并求出S的最大值;
②点Q是直线AB上的一个动点,若以AB'为边,点A,B',Q,P为顶点的四边形是平行四边形,请求出所有符合条件的t的值.
【分析】(1)利用旋转的性质得出A′(﹣1,0),B′(0,2),再利用待定系数法求二次函数解析式即可;
(2)①利用S四边形ABPB'=S△B′OP+S△PBO﹣S△AOB,可得四边形ABPB'的面积S与t的函数关系式,根据二次函数的性质即可求解;
②分四边形AB'PQ是平行四边形、四边形AB'QP是平行四边形两种情况,利用平行四边形的性质分别求解即可.
解:(1)△A′B′O是由△ABO绕原点O逆时针旋转90°得到的,
又A(0,1),B(2,0),O(0,0),
∴A′(﹣1,0),B′(0,2),
∵A′(﹣1,0),B′(0,2),B(2,0),
设抛物线的解析式为:y=a(x+1)(x﹣2)
将B′(0,2)代入得出:2=a(0+1)(0﹣2),
解得:a=﹣1,
故满足条件的抛物线的解析式为y=﹣(x+1)(x﹣2)=﹣x2+x+2;
(2)①如图:连接OP,
∵该抛物线的一个动点P的横坐标为t.
∴P(t,﹣t2+t+2),(0<t<2).
∵A(0,1),B(2,0),B′(0,2),
∴S四边形ABPB'=S△B′OP+S△PBO﹣S△AOB
=×2t+×2(﹣t2+t+2)﹣×2×1
=﹣t2+2t+1,
∴四边形ABPB'的面积S与t的函数关系式为S=﹣t2+2t+1(0<t<2),
∵S=﹣t2+2t+1=﹣(t﹣1)2+2,
∴当t=1时,S的最大值为2;
②如图,当四边形AB'PQ是平行四边形时,
∵四边形AB'PQ是平行四边形,
∴AB′∥PQ,AB′=PQ,
∵A(0,1),B′(0,2),
∴AB′=1,
设AB的解析式为y=kx+n,
∵A(0,1),B(2,0),
∴,解得,
∴AB的解析式为y=﹣x+1,
∵P(t,﹣t2+t+2),
∴Q(t,﹣t+1),
则PQ=﹣t2+t+2﹣(﹣t+1)=﹣t2+t+1=﹣(t﹣)2+=1,
解得t=0(舍去)或t=;
当四边形AB'QP是平行四边形时,
∴AB′∥PQ,AB′=PQ,
则PQ=﹣t+1﹣(﹣t2+t+2)=t2﹣t﹣1=(t﹣)2﹣=1,
解得t=或,
故所有符合条件的t的值为或或.
内容提要
(一)关于等腰三角形找点(作点)和求点的不同
(二)关于直角三角形找点和求点的方法
知识点拓展详解
(一)关于等腰三角形找点(作点)和求点的不同,
1、等腰三角形找点(作点)方法:以已知边为边长,作等腰三角形,运用两园一线法,在图上找出存在点的个数,只找不求。
2、等腰三角形求点方法:以已知边为边长,在抛物线或坐标轴或对称轴上找点,与已知点构成等腰三角形,先设所求点的坐标,然后根据两点间的距离公式求出三点间的线段长度,然后分顶点进行讨论,
(二)关于直角三角形找点和求点的方法
1、直角三角形找点(作点)方法:以已知边为边长,作直角三角形,运用两线一园法,在图上找出存在点的个数,只找不求。所谓的两线就是指以已知边为直角边,过已知边的两个端点分别作垂线与抛物线或坐标轴或对称轴的交点,就是所求的点;一圆就是以已知边为直径,以已知边的中点作圆,与抛物线或坐标轴或对称轴的交点即为所求的点。
2、具体方法
(1)121k k ;(2)三角形全等(注意寻找特殊角,如30°、60°、45°、90°)
(3)三角形相似;经常利用一线三等角模型
(4)勾股定理;
当题目中出现了特殊角时,优先考虑全等法
最新典型例题——教你解题
例题1.如图,抛物线y=x2﹣x﹣的图象与x轴交于点A,B,与y轴交于点C,顶点为D,以AB为直径在x轴上方画半圆交y轴于点E,圆心为I,P是半圆上一动点,连接DP,点Q为PD的中点.下列四种说法:①点C在⊙I上;②IQ⊥PD;③当点P沿半圆从点B运动至点A时,点Q运动的路径长为π;④线段BQ的长可以是3.2.
其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
【思路点拨】由抛物线y=x2﹣x﹣得A(﹣1,0),B(3,0),C(0,﹣),可得I(1,0),顶点D(1,﹣2),
①根据勾股定理求出IC,即可求解;
②根据垂径定理即可求解;
③点P的运动轨迹为以I为圆心的半圆,则点Q的运动轨迹为以R为圆心的半圆,即可求解;
④根据勾股定理即可求解.
【归纳总结】将函数知识与方程、几何知识有机地结合在一起.这类试题一般难度较大.解这类问题关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.
最新典型例题2.
如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc<0;③a+b≥am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【思路点拨】根据已知点的特点可求对称轴为直线x=1,则b=﹣2a;由函数的图象可知,a<0,c>0,再由b=﹣2a可知b>0;当x=1时,函数有最大值a+b+c;再由铅锤法求△BCQ的面积,从而确定当m=2时,三角形面积有最大值.
提高同步练习
一.选择题
1.如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点,抛物线的顶点为D,点C为AB的中点,以C为圆心,AC长为半径在x轴的上方作一个半圆,点E为半圆上一动点,连接DE,取DE的中点F,当点E沿着半圆从点A运动至点B的过程中,线段AF的最小值为( )
A. B. C. D.
2.如图,在平面直角坐标系中,抛物线y=与x轴的正半轴交于点A,B点为抛物线的顶点,C点为该抛物线对称轴上一点,则3BC+5AC的最小值为( )
A.24 B.25 C.30 D.36
3.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc>0;③a+b>am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=1,n=a+b+c,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,在△ABC中,∠ACB=90°,∠ABC=45°,BC=4,D为AC上一点,CD=.若E为AB边上一动点,连接DE,设BE=x,DE2=y,则y关于x的函数图象大致为( )
A. B. C. D.
5.设M为抛物线y=(x﹣1)2的顶点,点A、B为该抛物线上的两个动点,且MA⊥MB.连接点A、B,过M作MC⊥AB于点C,则点C到y轴距离的最大值( )
A. B. C. D.2
二.填空题(共4小题)
6.在平面直角坐标系中,抛物线y=x2﹣bx+c(b>0,b、c为常数)的顶点为A,与y轴交于点B,点B关于抛物线对称轴的对称点为C.若△ABC是等腰直角三角形,则BC的长为 .
7.如图,已知二次函数y=﹣x2+(a+1)x﹣a的图象与x轴交于A、B两点(点A位于点B的左侧),与y轴交于点C.已知△BAC的面积是6,若在抛物线上存在一点P(与点C不重合),使S△ABP=S△ABC,则点P的坐标为 .
8.如图,在平面直角坐标系中,点 A、点B均在抛物线y=x2上,且AB∥x轴,点 C、点D为线段AB的三等分点,以CD为边向下作矩形CDEF,矩形CDEF的顶点 E、F均在此抛物线上,若矩形CDEF的面积为2,则AB的长为 .
9.抛物线交x轴负半轴于点A,点B是抛物线上一动点,且点B在第二象限,以AB为边,作等腰直角三角形ABP.其中∠ABP=90°,当点P恰好在y轴上时,点P的坐标为 .
三.解答题(共3小题)
10.抛物线线L:y=ax2+bx+c(a≠0)与直线l:y=kx+m(k≠0)有且只有一个交点,我们就称此直线l与抛物线L的相切.直线l叫做抛物线L的切线,交点叫做抛物线L的切点.
(1)若点A为抛物线y=x2﹣2x+4与y轴的交点,求以点A为切点的该抛物线的切线的解析式;
(2)已知一次函数y1=2x,二次函数y2=x2+1,是否存在二次函数y3=ax2+bx+c,其图象经过点(﹣3,2),使得直线y1=2x与y2=x2+1,y3=ax2+bx+c都相切于同一点?若存在,求出y3的解析式;若不存在,请说明理由;
(3)已知直线l1:y=k1x+m1(k1≠0)、直线l2:y2=k2x+m2(k2≠0)是抛物线y=﹣x2+2x+3的两条切线,当l1与l2的交点P的纵坐标为5时,试判断k1 k2是否为定值,并说明理由.
11.如图,抛物线y=ax2+bx+3与x轴相交于A、B两点,与y轴相交于点C,已知B点的坐标为(6,0),抛物线的对称轴为直线x=2,点D是BC上方抛物线上的一个动点.
(1)求这个抛物线的解析式;
(2)当△BCD的面积为时,求点D的坐标;
(3)是否存在点D,使得∠DCB=2∠ABC?若存在,请求出点D的坐标;若不存在,请说明理由.
12.如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A'B'O.
(1)有一条抛物线经过点A',B',B,求该抛物线的解析式.
(2)设该抛物线的一个动点P的横坐标为t.
①当0<t<2时,求四边形ABPB'的面积S与t的函数关系式,并求出S的最大值;
②点Q是直线AB上的一个动点,若以AB'为边,点A,B',Q,P为顶点的四边形是平行四边形,请求出所有符合条件的t的值.
参考答案与试题解析
【教你解题】
最新典型例题1:如图,抛物线y=x2﹣x﹣的图象与x轴交于点A,B,与y轴交于点C,顶点为D,以AB为直径在x轴上方画半圆交y轴于点E,圆心为I,P是半圆上一动点,连接DP,点Q为PD的中点.下列四种说法:
①点C在⊙I上;
②IQ⊥PD;
③当点P沿半圆从点B运动至点A时,点Q运动的路径长为π;
④线段BQ的长可以是3.2.
其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
解:抛物线y=x2﹣x﹣的图象与坐标轴交于点A,B,C,
∴A(﹣1,0),B(3,0),C(0,﹣),
∴点I(1,0),⊙I的半径为2,
∵y=x2﹣x﹣=(x﹣1)2﹣2,
∴顶点D的坐标为:(1,﹣2),
∴ID=2,
∴点D在⊙I上.
①IC===≠2,故点C不在⊙I上,故①不正确;
②∵圆心为I,P是半圆上一动点,点D在⊙I上,点Q为PD的中点.
∴IQ⊥PD,故②正确;
③图中实点G、Q、I、F是点N运动中所处的位置,
则GF是等腰直角三角形的中位线,GF=AB=2,ID交GF于点R,则四边形GDFI为正方形,
当点P在半圆任意位置时,中点为Q,连接IQ,则IQ⊥PD,连接QR,
则QR=ID=IR=RD=RG=RF=GF=1,则点Q的运动轨迹为以R为圆心的半圆,
则Q运动的路径长=×2πr=π,故③正确;
④由③得,当点Q运动到点G的位置时,BQ的长最大,
最大值为=<3.2,
∴线段BQ的长不可以是3.2,故④不正确.
故正确说法有:②③.
故选:B.
最新典型例题2.如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc<0;③a+b≥am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
解:∵抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),B(4,0),
∴对称轴为直线x==1,
∴﹣=1,
∴2a=﹣b,
∴2a+b=0,故①正确,符合题意;
∵抛物线开口向下,
∴a<0,
∴b=﹣2a>0,
∵抛物线交y轴的正半轴,
∴c>0,
∴abc<0,故②正确,符合题意;
∵抛物线的对称轴x=1,开口向下,
∴x=1时,y有最大值,最大值=a+b+c.
∴a+b+c≥am2+bm+c(m为任意实数),
∴a+b≥am2+bm(m为任意实数),故③正确,符合题意;
④∵C(0,c),
设直线BC的解析式为y=kx+t,
∴,
解得,
∴y=﹣x+c,
将点A(﹣2,0)代入y=ax2﹣2ax+c,
∴c=﹣8a.
∴y=ax2﹣2ax﹣8a.
过点Q作QN∥y轴交BC于点P,
∵Q(m,n),
∴P(m,2am﹣8a),
∴PQ=n﹣2am+8a.
∴S△QBC=×4×(n﹣2am+8a)=2(n﹣2am+8a),
∵n=am2﹣2am﹣8a,
∴S△QBC=2(am2﹣4am)=2a(m﹣2)2﹣8a.
∴当m=2时,△QBC的面积最大,
故④正确,符合题意;
故选:D.
提高同步练习
一.选择题
1.如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点,抛物线的顶点为D,点C为AB的中点,以C为圆心,AC长为半径在x轴的上方作一个半圆,点E为半圆上一动点,连接DE,取DE的中点F,当点E沿着半圆从点A运动至点B的过程中,线段AF的最小值为( )
A. B. C. D.
【分析】由题意可知E点在以C为圆心,2为半径的半圆上,则F点在以G(1,﹣2)为圆心,1为半径的半圆上,AF的最小值为AG﹣1,求出AG即可求解.
解:连接AD、AE,
令y=0,则x2﹣2x﹣3=0,
解得x=3或x=﹣1,
∴A(﹣1,0),B(3,0),
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点D(1,﹣4),
∴AD的中点为H(0,﹣2),
连接HF,
∵F是DE的中点,
∴HF∥AE,HF=AE,
∵AB=4,C(2,0),
∴E点在以C为圆心,2为半径的半圆上,
∴F点在以G(1,﹣2)为圆心,1为半径的半圆上,
∴AG=2,
∴AF的最小值为2﹣1,
故选:C.
2.如图,在平面直角坐标系中,抛物线y=与x轴的正半轴交于点A,B点为抛物线的顶点,C点为该抛物线对称轴上一点,则3BC+5AC的最小值为( )
A.24 B.25 C.30 D.36
【分析】连接OB,过C点作CM⊥OB于M点,过A点作AN⊥OB于N点,抛物线的对称轴与x轴交于点D,先求出抛物线与坐标轴的交点坐标,继而得出BD、OA、OD,再证明△OBD∽△CBM,△OBD∽△OAN,进而可得3BC+5AC=5MC+5AC=5(AC+CM),当A、C、M三点共线,且三点连线垂直OB时,AC+CM最小,根据求出AN,AC+CM最小值即为AN,则问题得解.
解:连接OB,过C点作CM⊥OB于M点,过A点作AN⊥OB于N点,抛物线的对称轴与x轴交于点D,如图,
令y=0,得方程,
解得:x1=0,x2=6,
∴A点坐标为(6,0),即OA=6,
将配成顶点式得:,
∴B点坐标为(3,4),
∴BD=4,OD=3,
∵CM⊥OB,AN⊥OB,
∴∠BMC=∠ANO=90°,
根据抛物线对称轴的性质可知BD⊥OA,
∴∠BDO=90°,
在Rt△BDO中,
利用勾股定理得,
∵∠OBD=∠CBM,∠BDO=∠BMC=90°,
∴△OBD∽△CBM,
同理可证得△OBD∽△OAN,
∴,,
∴,即3BC=5MC,
∴3BC+5AC=5MC+5AC=5(AC+CM),
∵当A、C、M三点共线,且三点连线垂直OB时,AC+CM最小,
∴AC+CM最小值为AN,如图所示,
∵,
∴,
∴AC+CM最小值,
∴即3BC+5AC=5(AC+CM)=24.
故选:A.
3.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc>0;③a+b>am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=1,n=a+b+c,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据已知点的特点可求对称轴为直线x=1,则b=﹣2a;由函数的图象可知,a<0,c>0,再由b=﹣2a可知b>0;当x=1时,函数有最大值a+b+c;再由铅锤法求△BCQ的面积,从而确定当m=2时,三角形面积有最大值.
解:∵抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),B(4,0),
∴对称轴为直线x==1,
∴﹣=1,
∴2a=﹣b,
∴2a+b=0,故①正确,符合题意;
∵抛物线开口向下,
∴a<0,
∴b=﹣2a>0,
∵抛物线交y轴的正半轴,
∴c>0,
∴abc<0,故②错误,不符合题意;
∵抛物线的对称轴x=1,开口向下,
∴x=1时,y有最大值,最大值=a+b+c,
∴a+b+c≥am2+bm+c(m为任意实数),
∴a+b≥am2+bm(m为任意实数),故③错误,不符合题意;
④∵C(0,c),
设直线BC的解析式为y=kx+t,
∴,
解得,
∴y=﹣x+c,
将点A(﹣2,0)代入y=ax2﹣2ax+c,
∴c=﹣8a,
∴y=ax2﹣2ax﹣8a,
过点Q作QN∥y轴交BC于点P,
∵Q(m,n),
∴P(m,2am﹣8a),
∴PQ=n﹣2am+8a,
∴S△QBC=4×(n﹣2am+8a)=2(n﹣2am+8a),
∵n=am2﹣2am﹣8a,
∴S△QBC=2(am2﹣4am)=2a(m﹣2)2﹣8a,
∴当m=2时,△QBC的面积最大,
故④不正确,不符合题意;
故选:A.
4.如图,在△ABC中,∠ACB=90°,∠ABC=45°,BC=4,D为AC上一点,CD=.若E为AB边上一动点,连接DE,设BE=x,DE2=y,则y关于x的函数图象大致为( )
A. B. C. D.
【分析】过点D作DF⊥AB于点F,利用等腰直角三角形的性质求得线段AF,DF,AB的长度,利用含x的代数式表示出EF,再利用勾股定理即可求得y与x的函数解析式,利用二次函数的性质结合自变量x的取值范围即可得出结论.
解:过点D作DF⊥AB于点F,如图,
∵∠ACB=90°,∠ABC=45°,BC=4,
∴AB==8,∠A=45°,
∵DF⊥AB,
∴AF=DF=AD,
∵AC=BC=4,CD=,
∴AD=3,
∴AF=DF=3.
∴BF=AB﹣AF=5,
∵BE=x,
∴当点E在点F的下方时,EE=5﹣x,
当点E在点F的上方时,EF=x﹣5,
∵DE2=EF2+DF2,
∴y=(5﹣x)2+32=x2﹣10x+34(0≤x≤5)或y=(x﹣5)2+32=x2﹣10x+34(5<x≤8),
∴当0≤x≤5时,y有最大值为34,最小值为9,
当5<x≤8时,y有最大值为34,此时x=8,
又∵y=(5﹣x)2+32=x2﹣10x+34(0≤x≤5)或y=(x﹣5)2+32=x2﹣10x+34(5<x≤8)的图象为抛物线的一部分,
故选:C.
5.设M为抛物线y=(x﹣1)2的顶点,点A、B为该抛物线上的两个动点,且MA⊥MB.连接点A、B,过M作MC⊥AB于点C,则点C到y轴距离的最大值( )
A. B. C. D.2
【分析】如图,以M为原点建立新坐标系.过点B作BE⊥x轴于点E,过点A作AD⊥x轴于点D,AH⊥BE于点H,交y′轴于点G,设AB交y′轴于点K.首先证明直线AB经过定点K(0,1),判断出点C的运动轨迹,可得结论.
解:如图,以M为原点建立新坐标系.过点B作BE⊥x轴于点E,过点A作AD⊥x轴于点D,AH⊥BE于点H,交y′轴于点G,设AB交y′轴于点K.
则抛物线在新坐标系下的解析式y′=x2,顶点M(0,0).
设MD=a,ME=b,K(0,m),则AD=a2,BE=b2,
∵KG∥BH,
∴=,
∴=,
∴m=ab,
∵AM⊥MB,
∴∠AMB=∠ADM=∠BEM=90°,
∴∠AMD+∠BME=90°,∠BME+∠EBM=90°,
∴∠AMD=∠MBE,
∴△ADM∽△MEB,
∴=,
∴=,
∴ab=1,
∴m=1,
∴K(0,1),
∴MK=1,
∵AC⊥AB,
∴∠MCK=90°,
∴点C的运动轨迹是以MK为直径的圆,
∴当点C在y′的右边侧,到y′轴的距离为时,点C到y轴的距离最大,最大值为1+=.
故选:B.
二.填空题(共4小题)
6.在平面直角坐标系中,抛物线y=x2﹣bx+c(b>0,b、c为常数)的顶点为A,与y轴交于点B,点B关于抛物线对称轴的对称点为C.若△ABC是等腰直角三角形,则BC的长为 8 .
【分析】分别求出A(2b,c﹣b2),B(0,c),C(4b,c),再由等腰直角三角形斜边的中线等于斜边的一半,建立方程4b=2(c﹣c+b2),求出b的值即可求解.
解:∵y=x2﹣bx+c=(x﹣2b)2+c﹣b2,
∴顶点A(2b,c﹣b2),对称轴为直线x=2b,
当x=0时,y=c,
∴B(0,c),
∵点B关于抛物线对称轴的对称点为C,
∴C(4b,c),
∵△ABC是等腰直角三角形,
∴4b=2(c﹣c+b2),
解得b=0或b=2,
∵b>0,
∴b=2,
∴BC=8,
故答案为:8.
7.如图,已知二次函数y=﹣x2+(a+1)x﹣a的图象与x轴交于A、B两点(点A位于点B的左侧),与y轴交于点C.已知△BAC的面积是6,若在抛物线上存在一点P(与点C不重合),使S△ABP=S△ABC,则点P的坐标为 (﹣2,3)或(﹣1+,﹣3)或(﹣1﹣,﹣3) .
【分析】由y=﹣x2+(a+1)x﹣a,令y=0,即﹣x2+(a+1)x﹣a=0,可求出A、B坐标结合三角形的面积,解出a=﹣3;然后根据题意P的纵坐标为±3,分别代入解析式即可求得横坐标,从而求得P的坐标.
解:∵y=﹣x2+(a+1)x﹣a,
令x=0,则y=﹣a,
∴C(0,﹣a),
令y=0,即﹣x2+(a+1)x﹣a=0,
解得x1=a,x2=1,
由图象知:a<0,
∴A(a,0),B(1,0),
∵S△ABC=6,
∴(1﹣a)(﹣a)=6,
解得:a=﹣3,(a=4舍去);
∵a=﹣3,
∴y=﹣x2﹣2x+3,C(0,3),
∵S△ABP=S△ABC.
∴P点的纵坐标为±3,
把y=3代入y=﹣x2﹣2x+3得﹣x2﹣2x+3=3,解得x=﹣2或x=0(与点C重合,舍去);
把y=﹣3代入y=﹣x2﹣2x+3得﹣x2﹣2x+3=﹣3,解得x=﹣1+或x=﹣1﹣,
∴P点的坐标为(﹣2,3)或(﹣1+,﹣3)或(﹣1﹣,﹣3).
故答案为:(﹣2,3)或(﹣1+,﹣3)或(﹣1﹣,﹣3).
8.如图,在平面直角坐标系中,点 A、点B均在抛物线y=x2上,且AB∥x轴,点 C、点D为线段AB的三等分点,以CD为边向下作矩形CDEF,矩形CDEF的顶点 E、F均在此抛物线上,若矩形CDEF的面积为2,则AB的长为 3 .
【分析】设A(a,a2),则B(﹣a,a2),利用抛物线的对称性和点的坐标的特征得到AB=2a,点 A、点B到x轴的距离为a2,利用矩形的性质得到点 C、点D关于y轴对称,HD=HC=a,则E(﹣a,),F(a,),利用矩形的面积公式可得到关于a的方程,利用立方根的意义即可求得a值,则结论可求.
解:抛物线y=x2的对称轴为y轴,
∵点 A、点B均在抛物线y=x2上,且AB∥x轴,
∴点 A、点B关于y轴对称,
设A(a,a2),则B(﹣a,a2),a>0.
∴AB=2a,点 A、点B到x轴的距离为a2.
∵点 C、点D为线段AB的三等分点,
∴CD=a.
设CD与y轴交于点H,
由题意,点 C、点D关于y轴对称,
∴HD=HC=a,
∵矩形CDEF的顶点 E、F均在此抛物线上,
∴E(﹣a,),F(a,),
∵EF∥x轴,
∴点 E、F到x轴的距离为2,
∵AB∥x轴,
∴DE=CF=,
∵矩形CDEF的面积为2,
∴CD CF=2,
∴a =2,
∴,
∴a=.
∴AB=2a=3.
故答案为:3.
9.抛物线交x轴负半轴于点A,点B是抛物线上一动点,且点B在第二象限,以AB为边,作等腰直角三角形ABP.其中∠ABP=90°,当点P恰好在y轴上时,点P的坐标为 (0,1) .
【分析】如图,过点A作AC⊥x轴,过点B作CD⊥y轴于点D,交AC于点C,可证△ABC≌△BPD(AAS),AC=BD,BC=PD,设B(t,﹣t2﹣t+2),可得BD=﹣t,BC=t﹣(﹣3)=t+3,AC=﹣t2﹣t+2,D(0,﹣t2﹣t+2),建立方程求解即可得出答案.
解:如图,过点A作AC⊥x轴,过点B作CD⊥y轴于点D,交AC于点C,
则∠ACB=∠BDP=90°,
∴∠ABC+∠BAC=90°,
∵∠ABP=90°,
∴∠ABC+∠PBD=90°,
∴∠BAC=∠PBD,
∵△ABP是等腰直角三角形,
∴AB=BP,
∴△ABC≌△BPD(AAS),
∴AC=BD,BC=PD,
∵y=﹣x2﹣x+2,
当y=0时,﹣x2﹣x+2=0,
解得:x1=﹣3,x2=1,
∴A(﹣3,0),
设B(t,﹣t2﹣t+2),
则BD=﹣t,BC=t﹣(﹣3)=t+3,AC=﹣t2﹣t+2,D(0,﹣t2﹣t+2),
∴﹣t2﹣t+2=﹣t,
解得:t=﹣2或,
∵点B在第二象限,
∴t=﹣2,
∴B(﹣2,2),D(0,2),BC=DP=1,
∴P(0,1);
故答案为:(0,1).
三.解答题(共3小题)
10.抛物线线L:y=ax2+bx+c(a≠0)与直线l:y=kx+m(k≠0)有且只有一个交点,我们就称此直线l与抛物线L的相切.直线l叫做抛物线L的切线,交点叫做抛物线L的切点.
(1)若点A为抛物线y=x2﹣2x+4与y轴的交点,求以点A为切点的该抛物线的切线的解析式;
(2)已知一次函数y1=2x,二次函数y2=x2+1,是否存在二次函数y3=ax2+bx+c,其图象经过点(﹣3,2),使得直线y1=2x与y2=x2+1,y3=ax2+bx+c都相切于同一点?若存在,求出y3的解析式;若不存在,请说明理由;
(3)已知直线l1:y=k1x+m1(k1≠0)、直线l2:y2=k2x+m2(k2≠0)是抛物线y=﹣x2+2x+3的两条切线,当l1与l2的交点P的纵坐标为5时,试判断k1 k2是否为定值,并说明理由.
【分析】(1)联立得x2﹣(k+2)x=0,根据“抛物线的切点”的定义即可求解;
(2)联立得x2﹣2x+1=0,可得切点为(1,2),根据直线y1=2x与y2=x2+1,y3=ax2+bx+c都相切于同一点,可得经过点(﹣3,2),(1,2),利用待定系数法得,联立得ax2+(2a﹣2)x+2﹣3a=0,由Δ=(2a﹣2)2﹣4a(2﹣3a)=4a2+4﹣8a﹣8a+12a2=16a2﹣16a+4=(4a﹣2)2=0,可得,b=1,,即可得y3的解折式为;
(3)由l1与l2的交点P的纵坐标为5,令P(t,5),则直线l1:y=k1x﹣k1t+5、直线l2:y2=k2x﹣k2t+5,根据“抛物线的切点”的定义得k12+(4t﹣4)k1﹣4=0,,即k1,k2为x2+(4t﹣4)x﹣4=0的两根,由根与系数的关系可得k1 k2=﹣4.
解:(1)∵点A为抛物线y=x2﹣2x+4与y轴的交点,A为切点,
∴A(0,4),
设过点A的切线的解析式为y=kx+4,
联立,
整理得x2﹣(k+2)x=0,
解得x1=0,x2=k+2,
由“抛物线的切点”的定义得,
∴k+2=0,
∴k=﹣2,
∴以点A为切点的该抛物线的切线的解析式为y=﹣2x+4;
(2)∵直线y1=2x与相切,
联立,
整理得x2﹣2x+1=0,
解得x=1,
∴切点为(1,2),
又∵直线y1=2x与y2=x2+1,y3=ax2+bx+c都相切于同一点,
∴经过点(﹣3,2),(1,2),
∴,解得,
∴,
联立,
整理得ax2+(2a﹣2)x+2﹣3a=0,
∴Δ=(2a﹣2)2﹣4a(2﹣3a)=4a2+4﹣8a﹣8a+12a2=16a2﹣16a+4=(4a﹣2)2=0,
∴,b=1,,
∴y3的解折式为;
(3)k1 k2是定值,k1 k2=﹣4,理由如下:
∵l1与l2的交点P的纵坐标为5,
令P(t,5),
∴直线l1:y=k1x+m1=k1t+m1=5、直线l2:y2=k2x+m2=k2t+m2=5,
∴m1=5﹣k1t、直线l2:m2=5﹣k2t,
∴直线l1:y=k1x﹣k1t+5、直线l2:y2=k2x﹣k2t+5,
联立得x2+(k1﹣2)x﹣k1t+2=0,
由抛物线L的切线得:,
同理可得,
∴k1,k2为x2+(4t﹣4)x﹣4=0的两根,
∴k1 k2=﹣4.
11.如图,抛物线y=ax2+bx+3与x轴相交于A、B两点,与y轴相交于点C,已知B点的坐标为(6,0),抛物线的对称轴为直线x=2,点D是BC上方抛物线上的一个动点.
(1)求这个抛物线的解析式;
(2)当△BCD的面积为时,求点D的坐标;
(3)是否存在点D,使得∠DCB=2∠ABC?若存在,请求出点D的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法列方程组求解抛物线的解析式即可;
(2)如图,连接OD,设D(x,﹣x2+x+3),令x=0,则y=3,即C(0,3),而B(6,0),再分别表示S△BOC,S△DOC,S△BOD,再利用△BCD的面积为列方程求解即可;
(3)过D作DQ∥y轴交BC于Q,过C作CF⊥DQ于F,点D作DE⊥BC,垂足为点E,则CF∥x轴,可得∠FCB=∠ABC,证明CD=CQ,DF=FQ,设D(x,﹣x2+x+3),则Q(x,﹣x+3),F(x,3),再列方程求解即可.
解:(1)∵B点的坐标为(6,0),抛物线y=ax2+bx+3的对称轴为直线x=2,
∴,
解得:,
所以抛物线的解析式为y=﹣x2+x+3;
(2)连接OD,过点D作DE⊥OB于点E,如图,
设D(x,﹣x2+x+3),
∵点D是BC上方抛物线上的一个动点,
∴0<x<6.
∴DE=﹣x2+x+3,OE=x,
令x=0,则y=3,
∴C(0,3),
∴OC=3.
∵B(6,0),
∴OB=6.
∵S△BCD=S△DCO+S△DOB﹣S△OBC,△BCD的面积为,
∴×OC OE+×OB DE﹣×OB OC=,
∴×3×x+×6×(﹣x2+x+3)﹣×6×3=,
整理得:x2﹣6x+5=0.
解得:x=1或x=5,
∴D(1,)或(5,);
(3)存在点D,使得∠DCB=2∠ABC,理由:
过D作DQ∥y轴交BC于Q,交OB于点G,过C作CF⊥DQ于F,点D作DE⊥BC,垂足为点E,如图,
当∠DCB=2∠ABC时,
∵CF∥x轴,
∴∠FCB=∠ABC,
∴∠DCB=2∠FCB,
∴∠DCF=∠BCF,
在△DCF和△QCF中,
,
∴△DCF≌△QCF(ASA).
∴CD=CQ,DF=FQ,
设BC的解析式为:y=mx+n,
∴,
解得:,
∴直线BC的解析式y=﹣x+3
设D(x,﹣x2+x+3),
∵点D是BC上方抛物线上的一个动点,
∴0<x<6.
∴DG=﹣x2+x+3,OG=x,
则Q(x,﹣x+3),F(x,3),
∴FG=3,QG=﹣x+3.
∴DF=DG﹣FG=(﹣x2+x+3)﹣3=﹣x2+x,
FQ=FG﹣QG=3﹣(﹣x+3)=x,
∴﹣x2+x=x,
解得:x1=2,x2=0(不符合题意,舍去),
∴x=2.
∴D(2,4).
12.如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A'B'O.
(1)有一条抛物线经过点A',B',B,求该抛物线的解析式.
(2)设该抛物线的一个动点P的横坐标为t.
①当0<t<2时,求四边形ABPB'的面积S与t的函数关系式,并求出S的最大值;
②点Q是直线AB上的一个动点,若以AB'为边,点A,B',Q,P为顶点的四边形是平行四边形,请求出所有符合条件的t的值.
【分析】(1)利用旋转的性质得出A′(﹣1,0),B′(0,2),再利用待定系数法求二次函数解析式即可;
(2)①利用S四边形ABPB'=S△B′OP+S△PBO﹣S△AOB,可得四边形ABPB'的面积S与t的函数关系式,根据二次函数的性质即可求解;
②分四边形AB'PQ是平行四边形、四边形AB'QP是平行四边形两种情况,利用平行四边形的性质分别求解即可.
解:(1)△A′B′O是由△ABO绕原点O逆时针旋转90°得到的,
又A(0,1),B(2,0),O(0,0),
∴A′(﹣1,0),B′(0,2),
∵A′(﹣1,0),B′(0,2),B(2,0),
设抛物线的解析式为:y=a(x+1)(x﹣2)
将B′(0,2)代入得出:2=a(0+1)(0﹣2),
解得:a=﹣1,
故满足条件的抛物线的解析式为y=﹣(x+1)(x﹣2)=﹣x2+x+2;
(2)①如图:连接OP,
∵该抛物线的一个动点P的横坐标为t.
∴P(t,﹣t2+t+2),(0<t<2).
∵A(0,1),B(2,0),B′(0,2),
∴S四边形ABPB'=S△B′OP+S△PBO﹣S△AOB
=×2t+×2(﹣t2+t+2)﹣×2×1
=﹣t2+2t+1,
∴四边形ABPB'的面积S与t的函数关系式为S=﹣t2+2t+1(0<t<2),
∵S=﹣t2+2t+1=﹣(t﹣1)2+2,
∴当t=1时,S的最大值为2;
②如图,当四边形AB'PQ是平行四边形时,
∵四边形AB'PQ是平行四边形,
∴AB′∥PQ,AB′=PQ,
∵A(0,1),B′(0,2),
∴AB′=1,
设AB的解析式为y=kx+n,
∵A(0,1),B(2,0),
∴,解得,
∴AB的解析式为y=﹣x+1,
∵P(t,﹣t2+t+2),
∴Q(t,﹣t+1),
则PQ=﹣t2+t+2﹣(﹣t+1)=﹣t2+t+1=﹣(t﹣)2+=1,
解得t=0(舍去)或t=;
当四边形AB'QP是平行四边形时,
∴AB′∥PQ,AB′=PQ,
则PQ=﹣t+1﹣(﹣t2+t+2)=t2﹣t﹣1=(t﹣)2﹣=1,
解得t=或,
故所有符合条件的t的值为或或.
同课章节目录
