【新课标】24.8进球路线与最佳射门角 课件(共36张PPT)
文档属性
| 名称 | 【新课标】24.8进球路线与最佳射门角 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 00:00:00 | ||
图片预览









文档简介
(共36张PPT)
24.8进球路线与最佳射门角
沪科版 九年级下
教学内容分析
本节在学习圆心角和圆周角的基础上,研究足球进球路线与最佳射门角的问题,学会综合运用圆的知识来解决简单的实际问题。
教学目标
1.了解足球运动场上跑动线路中射门角的变化,掌握最佳射门角与圆的关系;(重点)
2.综合应用已学知识解决简单的实际问题,增强应用知识,提高实践能力;(难点)
3.体验数学知识与日常生活之间的密切联系,感受数学来源于生活也反作用于生活。
核心素养分析
本节在学习圆心角和圆周角等圆的知识基础上,研究足球进球路线与最佳射门角的问题,培养了学生解决实际问题的能力,感受数学来源于生活,又反作用生活。
新知导入
你看过世界杯足球赛吗?听过球场顺口溜吗?
球场顺口溜:
冲向球门跑,
越近就越好;
歪着球门跑,
射点要选好!
新知讲解
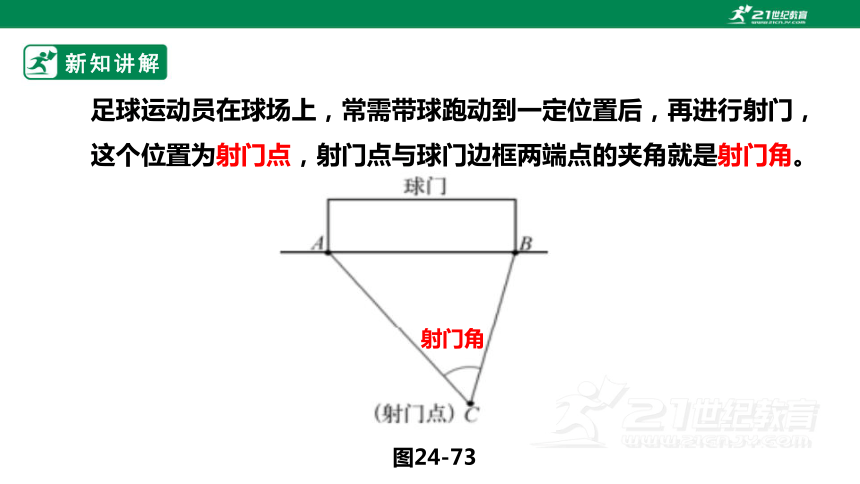
足球运动员在球场上,常需带球跑动到一定位置后,再进行射门,这个位置为射门点,射门点与球门边框两端点的夹角就是射门角。
图24-73
射门角
新知讲解
如图24-73,如果点A、B表示球门边框(不考虑球门的高度)的两端点,点C表示射门点,连接AC,BC,则∠ACB就是射门角。
图24-73
射门角
在不考虑其他因素的情况下,一般地,射门角越大,射门进球的可能性就越大。
新知讲解
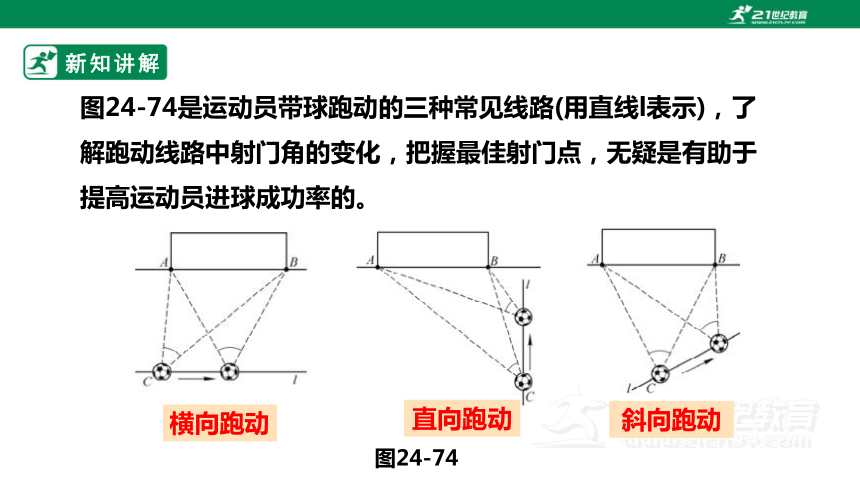
图24-74是运动员带球跑动的三种常见线路(用直线l表示),了解跑动线路中射门角的变化,把握最佳射门点,无疑是有助于提高运动员进球成功率的。
横向跑动
斜向跑动
直向跑动
图24-74
当运动员横向跑动时,射门角度会怎样变化呢?
新知讲解
新知讲解
探究1:横向跑动时,射门角度的变化情况
如图24-75,直线l与球门AB平行,点C表示运动员的位置,
当点C在直线l上由左边(或右边)逐渐向球门的中心靠近时,∠ACB逐渐增大。
图24-75
新知讲解
根据对称性可知,当点C在直线l上移动到离球门中心最近的位置,即线段AB的垂直平分线与直线I的交点C0时,∠AC0B最大。
图24-75
新知讲解
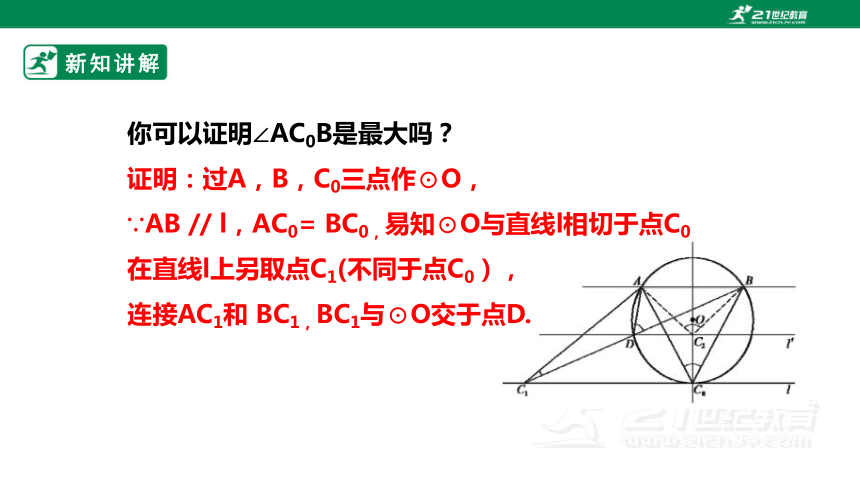
你可以证明∠AC0B是最大吗?
证明:过A,B,C0三点作⊙O,
∵AB // l,AC0= BC0,易知⊙O与直线l相切于点C0
在直线l上另取点C1(不同于点C0),
连接AC1和 BC1,BC1与⊙O交于点D.
新知讲解
则根据圆周角定理∠ADB =∠AC0B.
由外角定理知,∠ADB >∠AC1B,
∴∠AC0B > ∠AC1B.
即点C在直线l上移动时,∠ACB的最大值为∠AC0B.
当直线l向上平移到直线l′时,射门角度是怎么变化呢?
新知讲解
新知讲解
探究2:当直线l向上平移到直线l′时,射门角度是怎么变化呢?
在图24-76中,当直线l向上平移到直线l′时,C0→C2,∠AC0B →∠AC2B,且有∠AC2B > ∠AC0B.
图24-76
新知讲解
当运动员沿直线l横向跑动时,他的位置离球门的中心越近,射门角越大,离球门的中心最近(点C0)时,射门角最大,
我们把点C0称为直线l上的最佳射门点,∠AC0B称为直线I上的最佳射门角.
新知讲解
当直线l向上平移到直线l′时,射门角度是怎么变化呢?
最佳射门角的大小与直线l到AB的距离有关,
由图24-76知,当直线l与AB的距离越近,最佳射门角就越大,射门进球的可能性也就越大.
图24-76
冲向球门跑,越近就越好
新知讲解
如果⊙O过点A,B,而直线AB同侧的三点C1,C0,C2分别在⊙O外,⊙O上和⊙O内,
则有∠AC1B< ∠AC0B< ∠AC2B.
在弦的同侧,同弦所对的圆外角α、圆周角β和圆内角θ的大小关系为圆外角α<圆周角β<圆内角θ。
新知讲解
问题1:如图24-77,当运动员直向跑动时,球门AB与直线l垂直,点C是运动员的位置
(1)作出过A、B、C三点的圆,猜想当点C在直线l上移动时,直线l与该圆的位置关系;
直线l与该圆相交
A
B
C
D
l
图24-77
新知讲解
(2)当直线l与该圆有怎样的位置关系时,∠ACB是直线l上的最佳射门角;
A
B
C
D
l
l'
直线l与圆相切时,∠ACB是直线l上的最佳射门角
新知讲解
(3)已知AB =m,BD =n,当点C是直线l上的最佳射门点时,求CD的长;
解:如图,过点O作OE⊥AD,连接OB.
∴四边形OEDC是矩形,OE=CD.
在Rt△OEB中,
BE= OB=OC=DE=
由勾股定理得,
CD=OE=
A
B
C
D
图24-77
O.
E
新知讲解
(4)向左平移直线l到直线I',观察直线l上的最佳射门角与直线l'上的最佳射门角之间的大小关系,写出你的结论.
A
B
C
D
l
l'
图24-77
结论:直线I上的最佳射门角比直线I'上的最佳射门角小。
新知讲解
问题2:当运动员直向跑动时,直线l垂直穿过球门AB,点C时运动员的位置.
(1)∠ACB的大小是怎么变化的?
逐渐变大
(2)直线l上还有没有最佳射门点?
说明你的理由.
没有最佳射门点,因为∠ACB逐渐变大。
A
B
C
1.如图,点P在圆外,点M,N都在圆上,则下列角度大小关系正确的是( )
A.∠APB>∠AMB B.∠APB>∠ANB
C.∠APB<∠AMB D.∠ANB>∠AMB
课堂练习
C
M
A
B
P
N
新知讲解
解:连接AN,
由圆周角定理得∠AMB=∠ANB
∵∠APB<∠ANB
∴∠APB<∠AMB
故选C
M
A
B
P
N
课堂练习
2.如图,三名足球运动员在不同的位置射门,( )射门进球的可能性最大。
A.A位置
B.B位置
C.C位置
D.以上均可以
B
A
B
C
课堂练习
解:如图
∠C=∠F=∠MEN,
∵∠MBN>∠F,即∠MBN>∠C,
∵∠MEN>∠A,即∠C>∠A,
∴∠MBN>∠C>∠A,故选B.
F
A
B
C
E
M
N
3.如图,足球运动员在球门AB前横向带球准备射门,下列说法正确的是( )
A.在C处射门进球的可能性大
B.在D处射门进球的可能性大
C.在C ,D两处射门进球的可能性一样大
D.无法判断C,D两处哪处进球的可能性大
课堂练习
B
解:通过观察D处的射门角大于C处;
故A,C,D错误,B正确;
故答案为B.
课堂练习
课堂练习
4.探究 斜向跑动时最佳射门点的情况
问题:如图当运动员斜向跑动时,经过球框点A、B、及足球C作⊙O,
1)直线l与⊙O的有哪些位置关系?
2)l与⊙O相切时,最佳射门点及最佳
射门角又在哪里
3)试说明∠ACB、∠ADB、∠AC'B的数量关系
C
E
A
B
O
O'
D
C'
l
课堂练习
解:1)直线l与⊙O相交、相切、相离
2)直线l与⊙O相切时,最佳射门点在C',最佳射门角在∠AC'B
3)∠ACB<∠ADB=∠AC'B
C
E
A
B
O
O'
D
C'
C
课堂总结
进球路线与最佳射门角
2直向跑动时,射门角度的变化情况
1横向跑动时,射门角度的变化情况
板书设计
24.8进球路线与最佳射门角
1.横向跑动
2.直向跑动
作业布置
必做题:课本P67的第1-3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.8进球路线与最佳射门角
沪科版 九年级下
教学内容分析
本节在学习圆心角和圆周角的基础上,研究足球进球路线与最佳射门角的问题,学会综合运用圆的知识来解决简单的实际问题。
教学目标
1.了解足球运动场上跑动线路中射门角的变化,掌握最佳射门角与圆的关系;(重点)
2.综合应用已学知识解决简单的实际问题,增强应用知识,提高实践能力;(难点)
3.体验数学知识与日常生活之间的密切联系,感受数学来源于生活也反作用于生活。
核心素养分析
本节在学习圆心角和圆周角等圆的知识基础上,研究足球进球路线与最佳射门角的问题,培养了学生解决实际问题的能力,感受数学来源于生活,又反作用生活。
新知导入
你看过世界杯足球赛吗?听过球场顺口溜吗?
球场顺口溜:
冲向球门跑,
越近就越好;
歪着球门跑,
射点要选好!
新知讲解
足球运动员在球场上,常需带球跑动到一定位置后,再进行射门,这个位置为射门点,射门点与球门边框两端点的夹角就是射门角。
图24-73
射门角
新知讲解
如图24-73,如果点A、B表示球门边框(不考虑球门的高度)的两端点,点C表示射门点,连接AC,BC,则∠ACB就是射门角。
图24-73
射门角
在不考虑其他因素的情况下,一般地,射门角越大,射门进球的可能性就越大。
新知讲解
图24-74是运动员带球跑动的三种常见线路(用直线l表示),了解跑动线路中射门角的变化,把握最佳射门点,无疑是有助于提高运动员进球成功率的。
横向跑动
斜向跑动
直向跑动
图24-74
当运动员横向跑动时,射门角度会怎样变化呢?
新知讲解
新知讲解
探究1:横向跑动时,射门角度的变化情况
如图24-75,直线l与球门AB平行,点C表示运动员的位置,
当点C在直线l上由左边(或右边)逐渐向球门的中心靠近时,∠ACB逐渐增大。
图24-75
新知讲解
根据对称性可知,当点C在直线l上移动到离球门中心最近的位置,即线段AB的垂直平分线与直线I的交点C0时,∠AC0B最大。
图24-75
新知讲解
你可以证明∠AC0B是最大吗?
证明:过A,B,C0三点作⊙O,
∵AB // l,AC0= BC0,易知⊙O与直线l相切于点C0
在直线l上另取点C1(不同于点C0),
连接AC1和 BC1,BC1与⊙O交于点D.
新知讲解
则根据圆周角定理∠ADB =∠AC0B.
由外角定理知,∠ADB >∠AC1B,
∴∠AC0B > ∠AC1B.
即点C在直线l上移动时,∠ACB的最大值为∠AC0B.
当直线l向上平移到直线l′时,射门角度是怎么变化呢?
新知讲解
新知讲解
探究2:当直线l向上平移到直线l′时,射门角度是怎么变化呢?
在图24-76中,当直线l向上平移到直线l′时,C0→C2,∠AC0B →∠AC2B,且有∠AC2B > ∠AC0B.
图24-76
新知讲解
当运动员沿直线l横向跑动时,他的位置离球门的中心越近,射门角越大,离球门的中心最近(点C0)时,射门角最大,
我们把点C0称为直线l上的最佳射门点,∠AC0B称为直线I上的最佳射门角.
新知讲解
当直线l向上平移到直线l′时,射门角度是怎么变化呢?
最佳射门角的大小与直线l到AB的距离有关,
由图24-76知,当直线l与AB的距离越近,最佳射门角就越大,射门进球的可能性也就越大.
图24-76
冲向球门跑,越近就越好
新知讲解
如果⊙O过点A,B,而直线AB同侧的三点C1,C0,C2分别在⊙O外,⊙O上和⊙O内,
则有∠AC1B< ∠AC0B< ∠AC2B.
在弦的同侧,同弦所对的圆外角α、圆周角β和圆内角θ的大小关系为圆外角α<圆周角β<圆内角θ。
新知讲解
问题1:如图24-77,当运动员直向跑动时,球门AB与直线l垂直,点C是运动员的位置
(1)作出过A、B、C三点的圆,猜想当点C在直线l上移动时,直线l与该圆的位置关系;
直线l与该圆相交
A
B
C
D
l
图24-77
新知讲解
(2)当直线l与该圆有怎样的位置关系时,∠ACB是直线l上的最佳射门角;
A
B
C
D
l
l'
直线l与圆相切时,∠ACB是直线l上的最佳射门角
新知讲解
(3)已知AB =m,BD =n,当点C是直线l上的最佳射门点时,求CD的长;
解:如图,过点O作OE⊥AD,连接OB.
∴四边形OEDC是矩形,OE=CD.
在Rt△OEB中,
BE= OB=OC=DE=
由勾股定理得,
CD=OE=
A
B
C
D
图24-77
O.
E
新知讲解
(4)向左平移直线l到直线I',观察直线l上的最佳射门角与直线l'上的最佳射门角之间的大小关系,写出你的结论.
A
B
C
D
l
l'
图24-77
结论:直线I上的最佳射门角比直线I'上的最佳射门角小。
新知讲解
问题2:当运动员直向跑动时,直线l垂直穿过球门AB,点C时运动员的位置.
(1)∠ACB的大小是怎么变化的?
逐渐变大
(2)直线l上还有没有最佳射门点?
说明你的理由.
没有最佳射门点,因为∠ACB逐渐变大。
A
B
C
1.如图,点P在圆外,点M,N都在圆上,则下列角度大小关系正确的是( )
A.∠APB>∠AMB B.∠APB>∠ANB
C.∠APB<∠AMB D.∠ANB>∠AMB
课堂练习
C
M
A
B
P
N
新知讲解
解:连接AN,
由圆周角定理得∠AMB=∠ANB
∵∠APB<∠ANB
∴∠APB<∠AMB
故选C
M
A
B
P
N
课堂练习
2.如图,三名足球运动员在不同的位置射门,( )射门进球的可能性最大。
A.A位置
B.B位置
C.C位置
D.以上均可以
B
A
B
C
课堂练习
解:如图
∠C=∠F=∠MEN,
∵∠MBN>∠F,即∠MBN>∠C,
∵∠MEN>∠A,即∠C>∠A,
∴∠MBN>∠C>∠A,故选B.
F
A
B
C
E
M
N
3.如图,足球运动员在球门AB前横向带球准备射门,下列说法正确的是( )
A.在C处射门进球的可能性大
B.在D处射门进球的可能性大
C.在C ,D两处射门进球的可能性一样大
D.无法判断C,D两处哪处进球的可能性大
课堂练习
B
解:通过观察D处的射门角大于C处;
故A,C,D错误,B正确;
故答案为B.
课堂练习
课堂练习
4.探究 斜向跑动时最佳射门点的情况
问题:如图当运动员斜向跑动时,经过球框点A、B、及足球C作⊙O,
1)直线l与⊙O的有哪些位置关系?
2)l与⊙O相切时,最佳射门点及最佳
射门角又在哪里
3)试说明∠ACB、∠ADB、∠AC'B的数量关系
C
E
A
B
O
O'
D
C'
l
课堂练习
解:1)直线l与⊙O相交、相切、相离
2)直线l与⊙O相切时,最佳射门点在C',最佳射门角在∠AC'B
3)∠ACB<∠ADB=∠AC'B
C
E
A
B
O
O'
D
C'
C
课堂总结
进球路线与最佳射门角
2直向跑动时,射门角度的变化情况
1横向跑动时,射门角度的变化情况
板书设计
24.8进球路线与最佳射门角
1.横向跑动
2.直向跑动
作业布置
必做题:课本P67的第1-3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
