图形的平移与旋转单元综合检测(附答案)
文档属性
| 名称 | 图形的平移与旋转单元综合检测(附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 316.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-18 00:00:00 | ||
图片预览

文档简介
单元综合检测(三)
第三章
(45分钟 100分)
一、选择题(每小题4分,共28分)
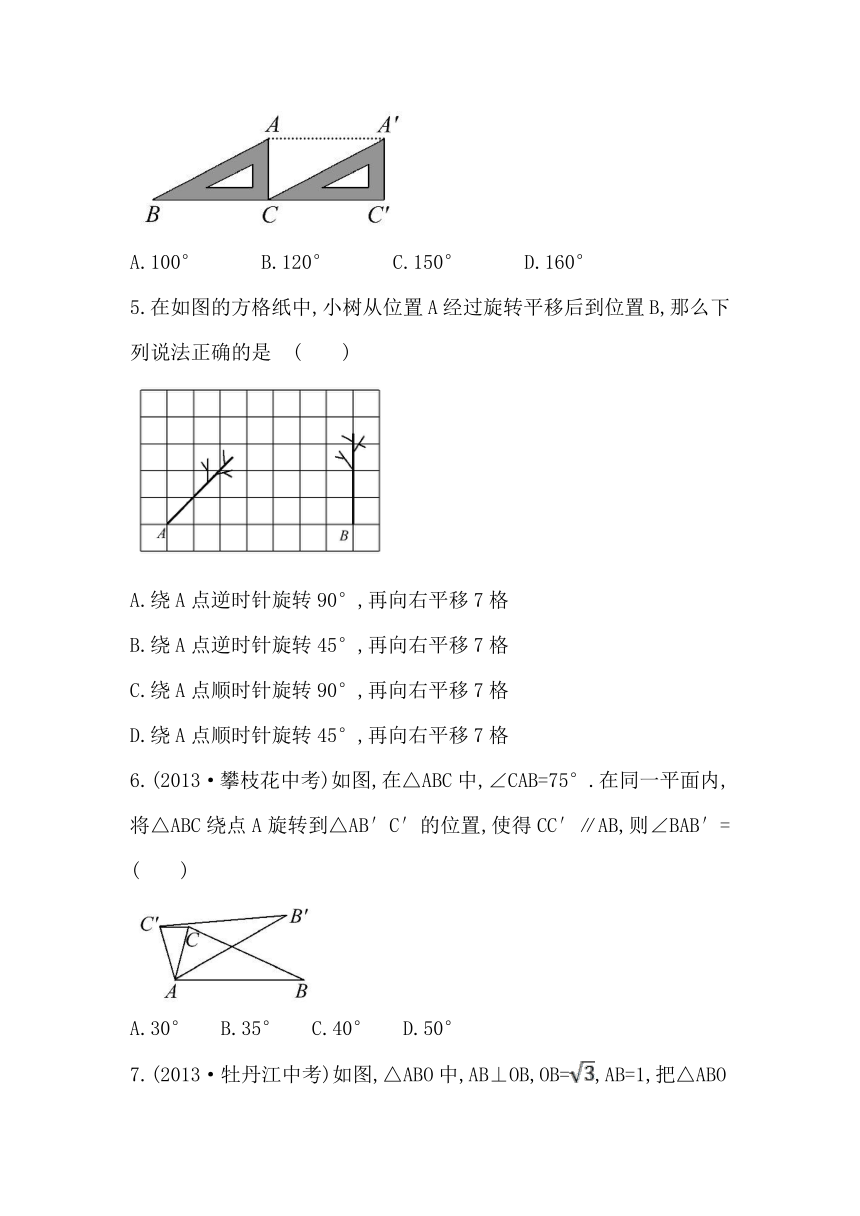
1.(2013·眉山中考)下列图形是中心对称图形的是 ( )
2.如图,△DEF经过怎样的平移得到△ABC ( )
A.把△DEF向左平移4个单位,再向下平移2个单位
B.把△DEF向右平移4个单位,再向下平移2个单位
C.把△DEF向右平移4个单位,再向上平移2个单位
D.把△DEF向左平移4个单位,再向上平移2个单位
3.(2013·潍坊中考)下面的图形是天气预报中的图标,其中既是轴对称图形又是中心对称图形的是 ( )
4.如图,将直角三角板ABC沿BC方向平移,得到△A′CC′.已知∠B=30°,∠ACB=90°,则∠BAA′的度数为 ( )
A.100° B.120° C.150° D.160°
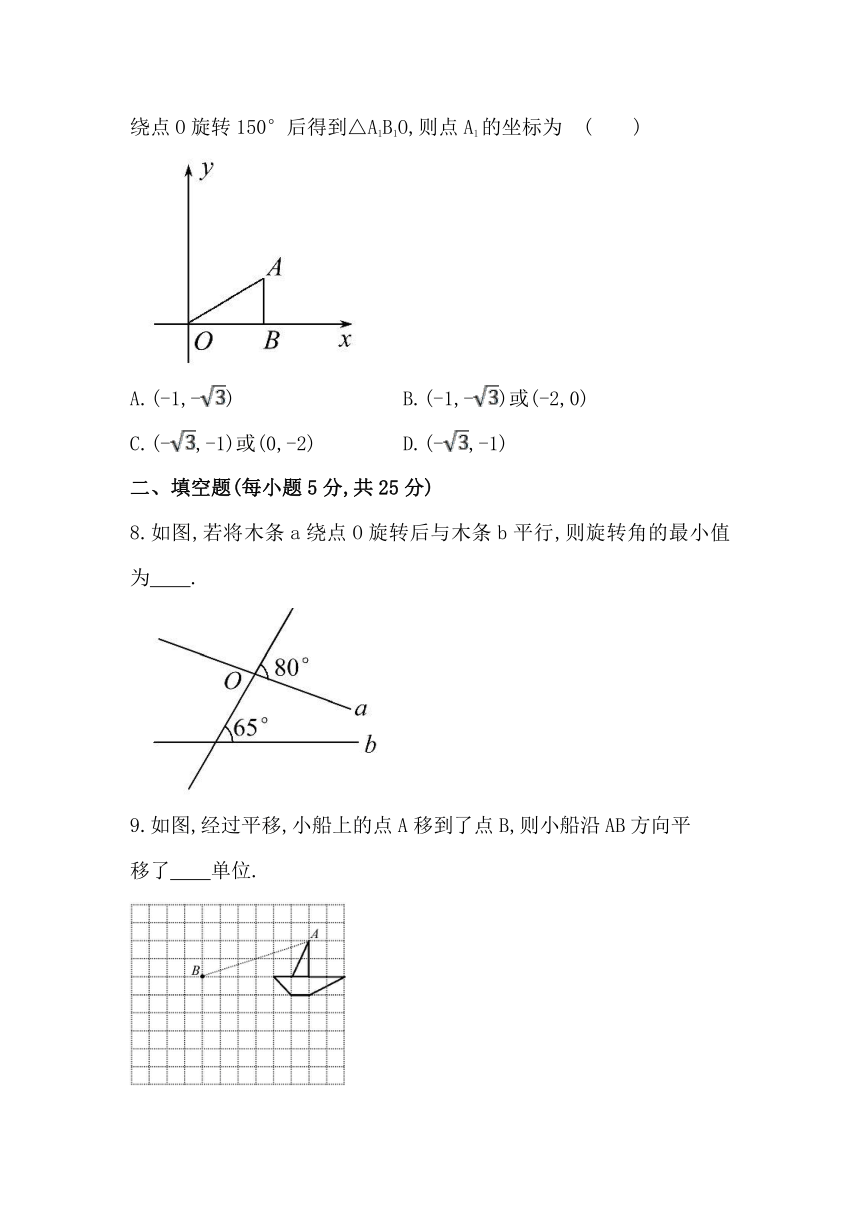
5.在如图的方格纸中,小树从位置A经过旋转平移后到位置B,那么下列说法正确的是 ( )
A.绕A点逆时针旋转90°,再向右平移7格
B.绕A点逆时针旋转45°,再向右平移7格
C.绕A点顺时针旋转90°,再向右平移7格
D.绕A点顺时针旋转45°,再向右平移7格
6.(2013·攀枝花中考)如图,在△ABC中,∠CAB=75°.在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′= ( )
A.30° B.35° C.40° D.50°
7.(2013·牡丹江中考)如图,△ABO中,AB⊥OB,OB=,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为 ( )
A.(-1,-) B.(-1,-)或(-2,0)
C.(-,-1)或(0,-2) D.(-,-1)
二、填空题(每小题5分,共25分)
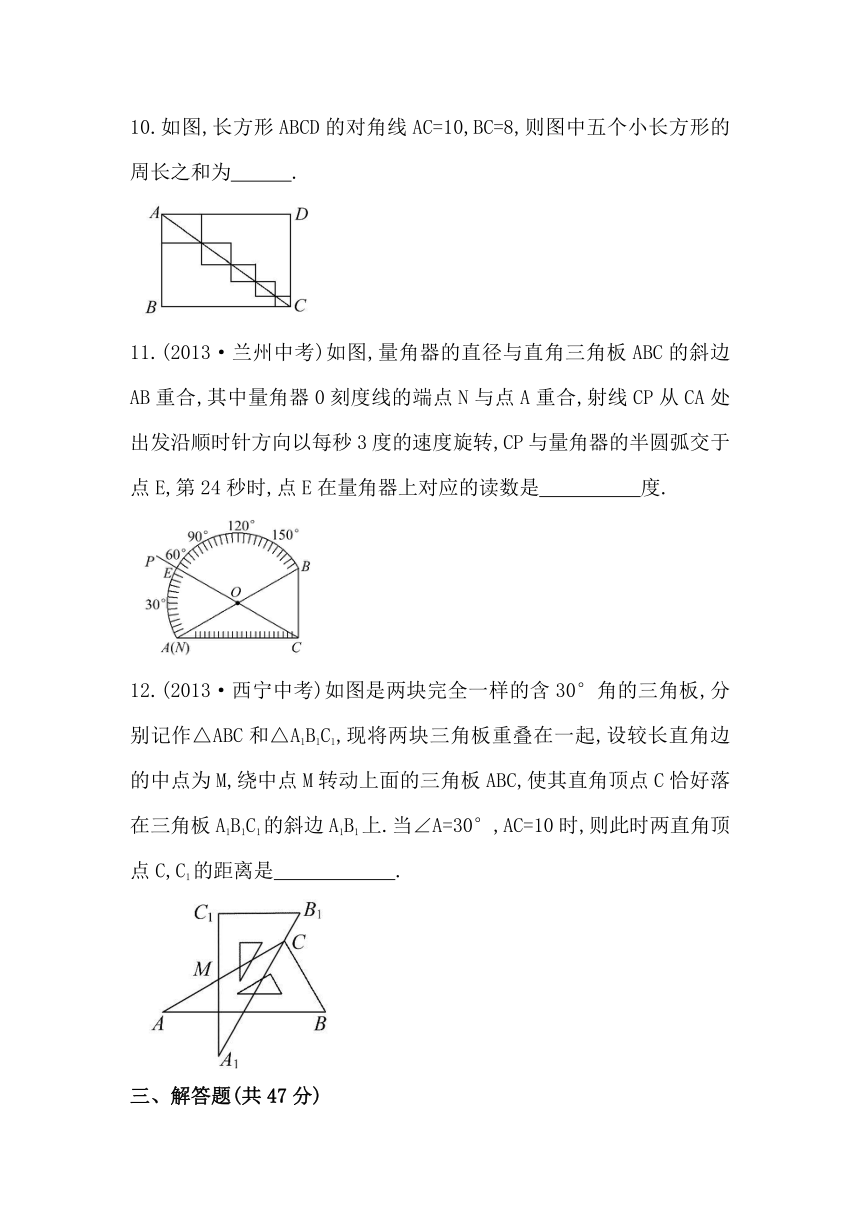
8.如图,若将木条a绕点O旋转后与木条b平行,则旋转角的最小值为 .
9.如图,经过平移,小船上的点A移到了点B,则小船沿AB方向平
移了 单位.
10.如图,长方形ABCD的对角线AC=10,BC=8,则图中五个小长方形的周长之和为 .
11.(2013·兰州中考)如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒时,点E在量角器上对应的读数是 度.
12.(2013·西宁中考)如图是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上.当∠A=30°,AC=10时,则此时两直角顶点C,C1的距离是 .
三、解答题(共47分)
13.(10分)下图中的六边形中的图案是怎样形成的
14.(12分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点
△ABC(顶点是网格线的交点)和点A1.
(1)画出一个格点△A1B1C1,并使它与△ABC全等且A与A1是对应点.
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样旋转而得到的.
15.(12分)已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,
∠EDF绕D点旋转,它的两边分别交AC,CB(或它们的延长线)于E,F.当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证S△DEF+S△CEF=S△ABC.当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立 若成立,请给予证明;若不成立,S△DEF、S△CEF、S△ABC又有怎样的数量关系 请写出你的猜想.
16.(13分)(2013·常州中考)在Rt△ABC中,∠ACB=90°,AC=1,BC=,点O为
Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,按下列要求画图(保留画图痕迹):
以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A,O的对应点分别为点A′,O′),并回答下列问题:
∠ABC= ,∠A′BC= ,OA+OB+OC= .
答案解析
1. B.
2. A.
3. A.
4. C..
5. B.
6 A.
7. B.
8. 15°
9. 2
10. 28
11. 144
12. 5
13. (1)可看作相邻两个图案绕中心旋转180°得到.
(2)可看作图案依次绕中心旋转60°,共旋转5次得到.
(3)可看作图案依次绕中心旋转60°,共旋转5次得到.
(4)可看作图案依次绕中心旋转120°,共旋转2次得到.
14. 1)如图,
答案不唯一
(2)作出图形,AD可以看作是由AB绕A点逆时针旋转90°而得到的.
15.图2成立;图3不成立.
证明图2:过点D作DM⊥AC,DN⊥BC,则∠DME=∠DNF=∠MDN=90°,再证∠MDE=
∠NDF,DM=DN,
故有△DME≌△DNF.所以S△DME=S△DNF.
所以S四边形DMCN=S四边形DECF=S△DEF+S△CEF.
由信息可知S四边形DMCN=S△ABC,
所以S△DEF+S△CEF=S△ABC.
图3不成立,
S△DEF、S△CEF、S△ABC的关系是:
S△DEF-S△CEF=S△ABC.
16.如图:
在Rt△ABC中,∠ACB=90°,AC=1,BC=,
所以∠ABC=30°,
由旋转可知∠AB A′=60°,
又因为∠A′BC=∠ABC+∠AB A′,
所以∠A′BC=90°,
连接OO′,由旋转可知OB=O′B,∠OBO′=60°,
所以△OBO′是正三角形,
所以∠BOO′=∠B O′O=60°,
又因为∠A′O′B=∠AOB=∠COB=120°,
所以CO,OO′,O′A′在一条直线上,
由旋转易得:OA =O′A′,OB=O′B=OO′,
所以OA+OB+OC=CA′,
在Rt△A′BC中,A′B=AB=2,BC=,
所以A′C==.
即OA+OB+OC=.
第三章
(45分钟 100分)
一、选择题(每小题4分,共28分)
1.(2013·眉山中考)下列图形是中心对称图形的是 ( )
2.如图,△DEF经过怎样的平移得到△ABC ( )
A.把△DEF向左平移4个单位,再向下平移2个单位
B.把△DEF向右平移4个单位,再向下平移2个单位
C.把△DEF向右平移4个单位,再向上平移2个单位
D.把△DEF向左平移4个单位,再向上平移2个单位
3.(2013·潍坊中考)下面的图形是天气预报中的图标,其中既是轴对称图形又是中心对称图形的是 ( )
4.如图,将直角三角板ABC沿BC方向平移,得到△A′CC′.已知∠B=30°,∠ACB=90°,则∠BAA′的度数为 ( )
A.100° B.120° C.150° D.160°
5.在如图的方格纸中,小树从位置A经过旋转平移后到位置B,那么下列说法正确的是 ( )
A.绕A点逆时针旋转90°,再向右平移7格
B.绕A点逆时针旋转45°,再向右平移7格
C.绕A点顺时针旋转90°,再向右平移7格
D.绕A点顺时针旋转45°,再向右平移7格
6.(2013·攀枝花中考)如图,在△ABC中,∠CAB=75°.在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′= ( )
A.30° B.35° C.40° D.50°
7.(2013·牡丹江中考)如图,△ABO中,AB⊥OB,OB=,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为 ( )
A.(-1,-) B.(-1,-)或(-2,0)
C.(-,-1)或(0,-2) D.(-,-1)
二、填空题(每小题5分,共25分)
8.如图,若将木条a绕点O旋转后与木条b平行,则旋转角的最小值为 .
9.如图,经过平移,小船上的点A移到了点B,则小船沿AB方向平
移了 单位.
10.如图,长方形ABCD的对角线AC=10,BC=8,则图中五个小长方形的周长之和为 .
11.(2013·兰州中考)如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒时,点E在量角器上对应的读数是 度.
12.(2013·西宁中考)如图是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上.当∠A=30°,AC=10时,则此时两直角顶点C,C1的距离是 .
三、解答题(共47分)
13.(10分)下图中的六边形中的图案是怎样形成的
14.(12分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点
△ABC(顶点是网格线的交点)和点A1.
(1)画出一个格点△A1B1C1,并使它与△ABC全等且A与A1是对应点.
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样旋转而得到的.
15.(12分)已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,
∠EDF绕D点旋转,它的两边分别交AC,CB(或它们的延长线)于E,F.当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证S△DEF+S△CEF=S△ABC.当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立 若成立,请给予证明;若不成立,S△DEF、S△CEF、S△ABC又有怎样的数量关系 请写出你的猜想.
16.(13分)(2013·常州中考)在Rt△ABC中,∠ACB=90°,AC=1,BC=,点O为
Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,按下列要求画图(保留画图痕迹):
以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A,O的对应点分别为点A′,O′),并回答下列问题:
∠ABC= ,∠A′BC= ,OA+OB+OC= .
答案解析
1. B.
2. A.
3. A.
4. C..
5. B.
6 A.
7. B.
8. 15°
9. 2
10. 28
11. 144
12. 5
13. (1)可看作相邻两个图案绕中心旋转180°得到.
(2)可看作图案依次绕中心旋转60°,共旋转5次得到.
(3)可看作图案依次绕中心旋转60°,共旋转5次得到.
(4)可看作图案依次绕中心旋转120°,共旋转2次得到.
14. 1)如图,
答案不唯一
(2)作出图形,AD可以看作是由AB绕A点逆时针旋转90°而得到的.
15.图2成立;图3不成立.
证明图2:过点D作DM⊥AC,DN⊥BC,则∠DME=∠DNF=∠MDN=90°,再证∠MDE=
∠NDF,DM=DN,
故有△DME≌△DNF.所以S△DME=S△DNF.
所以S四边形DMCN=S四边形DECF=S△DEF+S△CEF.
由信息可知S四边形DMCN=S△ABC,
所以S△DEF+S△CEF=S△ABC.
图3不成立,
S△DEF、S△CEF、S△ABC的关系是:
S△DEF-S△CEF=S△ABC.
16.如图:
在Rt△ABC中,∠ACB=90°,AC=1,BC=,
所以∠ABC=30°,
由旋转可知∠AB A′=60°,
又因为∠A′BC=∠ABC+∠AB A′,
所以∠A′BC=90°,
连接OO′,由旋转可知OB=O′B,∠OBO′=60°,
所以△OBO′是正三角形,
所以∠BOO′=∠B O′O=60°,
又因为∠A′O′B=∠AOB=∠COB=120°,
所以CO,OO′,O′A′在一条直线上,
由旋转易得:OA =O′A′,OB=O′B=OO′,
所以OA+OB+OC=CA′,
在Rt△A′BC中,A′B=AB=2,BC=,
所以A′C==.
即OA+OB+OC=.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
