2023年中考数学二轮复习压轴题专题讲义 第八讲“辅助圆”模型求最值模型专题(含答案)
文档属性
| 名称 | 2023年中考数学二轮复习压轴题专题讲义 第八讲“辅助圆”模型求最值模型专题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 909.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 15:08:35 | ||
图片预览

文档简介
第八讲 “辅助圆”模型求最值模型(专题讲义)
内容提要
隐圆模型
(1)动点到定点定长模型
(2)直角圆周角模型
(3)定边对定角模型
(4)四点共圆模型①
(5)四点共圆模型②
知识点拓展详解
隐圆模型
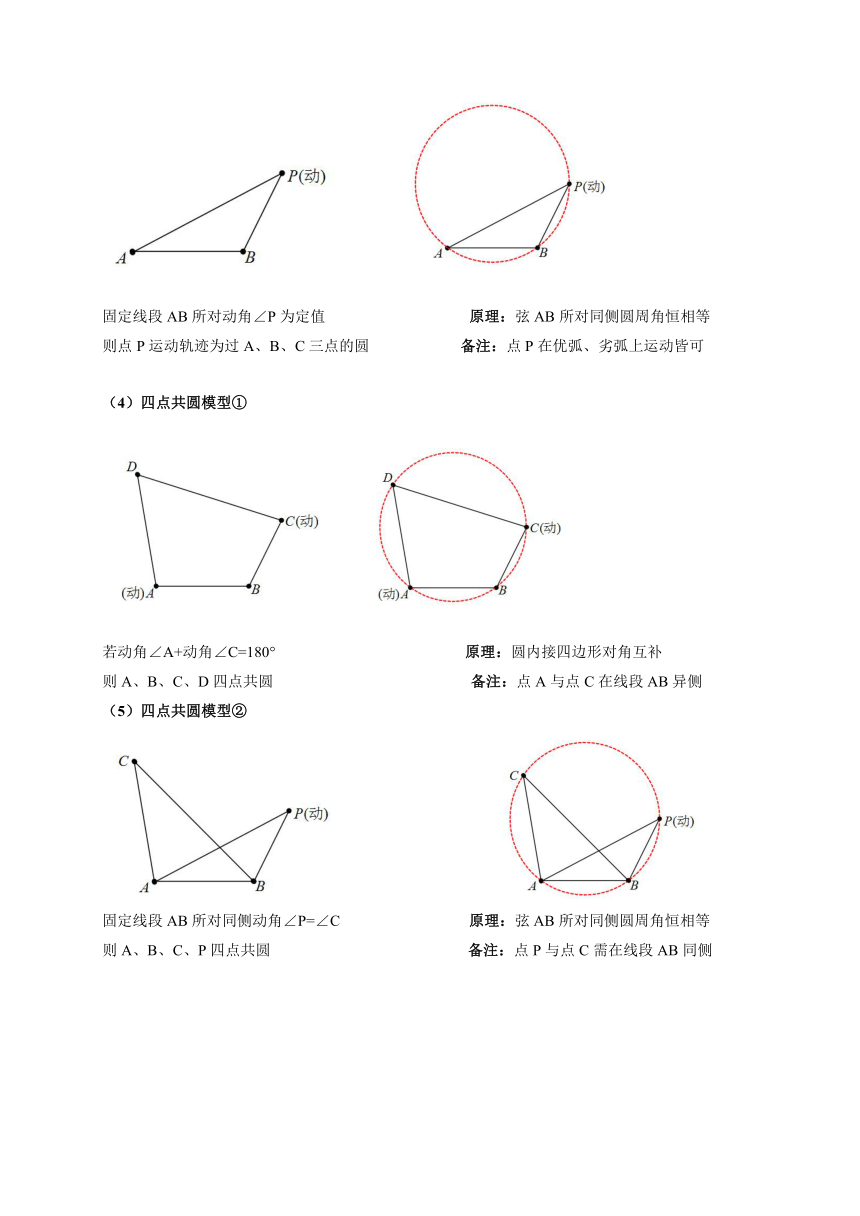
(1)动点到定点定长模型(共顶点的三条等线段)
若P为动点,但AB=AC=AP 原理:圆A中,AB=AC=AP
则B、C、P三点共圆,A圆心,AB半径 备注:常转全等或相似证明出定长
(2)直角圆周角模型
固定线段AB所对动角∠C恒为90° 原理:圆O中,圆周角为90°所对弦是直径
则A、B、C三点共圆,AB为直径 备注:常通过互余转换等证明出动角恒为直角
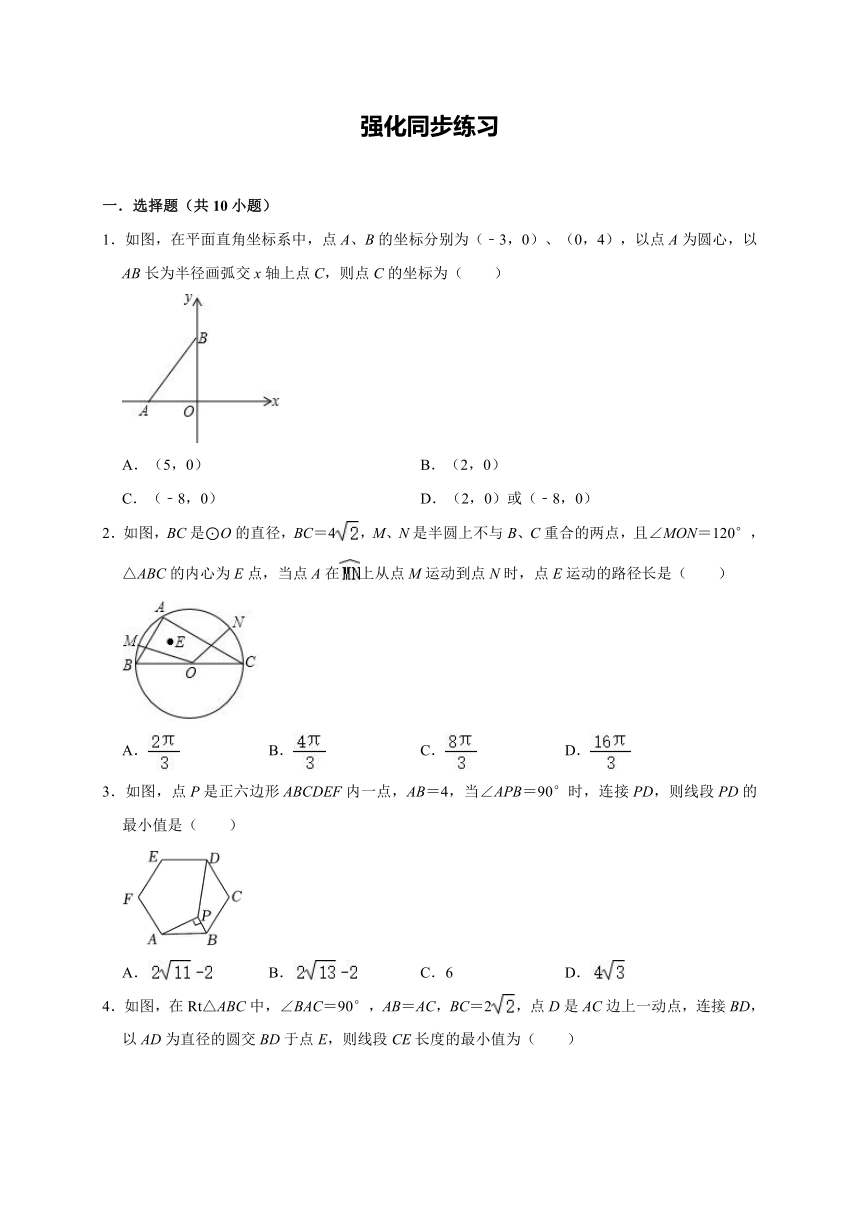
(3)定边对定角模型
固定线段AB所对动角∠P为定值 原理:弦AB所对同侧圆周角恒相等
则点P运动轨迹为过A、B、C三点的圆 备注:点P在优弧、劣弧上运动皆可
(4)四点共圆模型①
若动角∠A+动角∠C=180° 原理:圆内接四边形对角互补
则A、B、C、D四点共圆 备注:点A与点C在线段AB异侧
(5)四点共圆模型②
固定线段AB所对同侧动角∠P=∠C 原理:弦AB所对同侧圆周角恒相等
则A、B、C、P四点共圆 备注:点P与点C需在线段AB同侧
强化同步练习
一.选择题(共10小题)
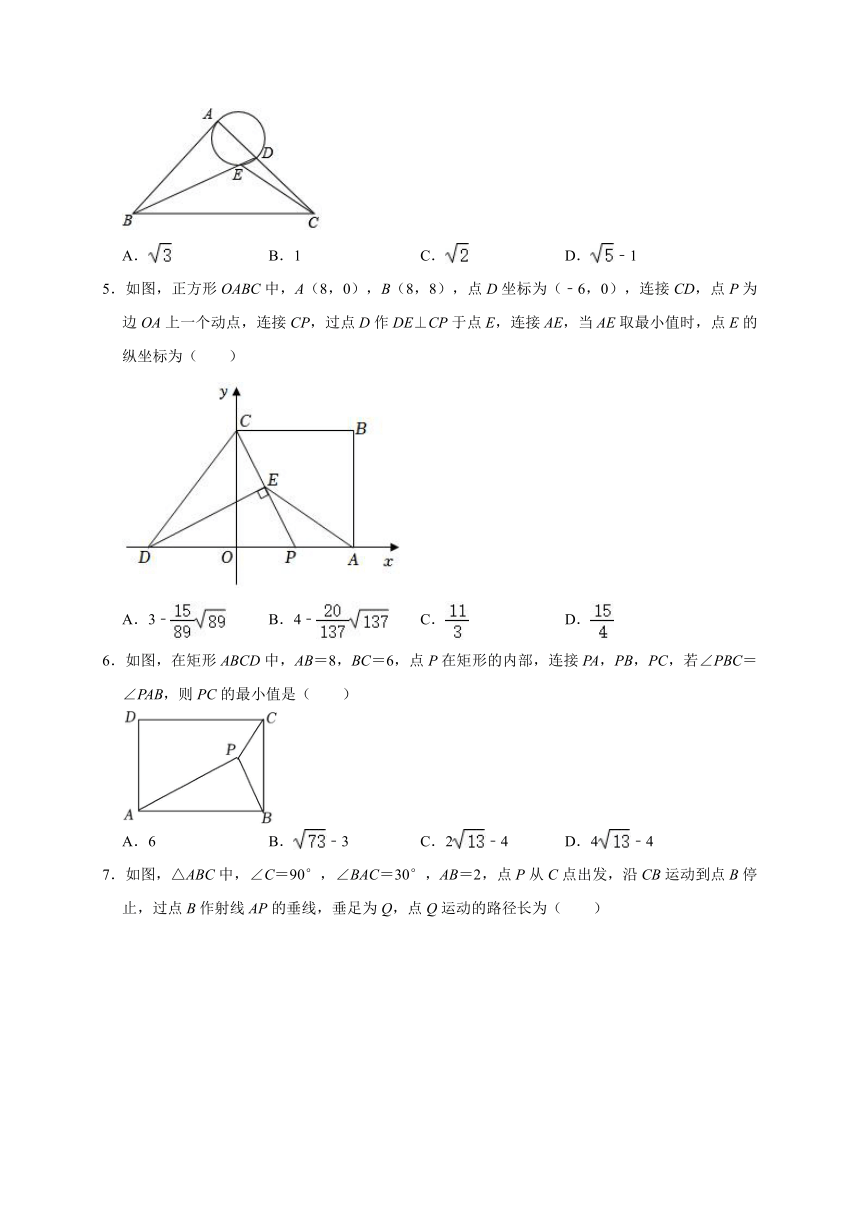
1.如图,在平面直角坐标系中,点A、B的坐标分别为(﹣3,0)、(0,4),以点A为圆心,以AB长为半径画弧交x轴上点C,则点C的坐标为( )
A.(5,0) B.(2,0)
C.(﹣8,0) D.(2,0)或(﹣8,0)
2.如图,BC是⊙O的直径,BC=4,M、N是半圆上不与B、C重合的两点,且∠MON=120°,△ABC的内心为E点,当点A在上从点M运动到点N时,点E运动的路径长是( )
A. B. C. D.
3.如图,点P是正六边形ABCDEF内一点,AB=4,当∠APB=90°时,连接PD,则线段PD的最小值是( )
A. B. C.6 D.
4.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
A. B.1 C. D.﹣1
5.如图,正方形OABC中,A(8,0),B(8,8),点D坐标为(﹣6,0),连接CD,点P为边OA上一个动点,连接CP,过点D作DE⊥CP于点E,连接AE,当AE取最小值时,点E的纵坐标为( )
A.3﹣ B.4﹣ C. D.
6.如图,在矩形ABCD中,AB=8,BC=6,点P在矩形的内部,连接PA,PB,PC,若∠PBC=∠PAB,则PC的最小值是( )
A.6 B.﹣3 C.2﹣4 D.4﹣4
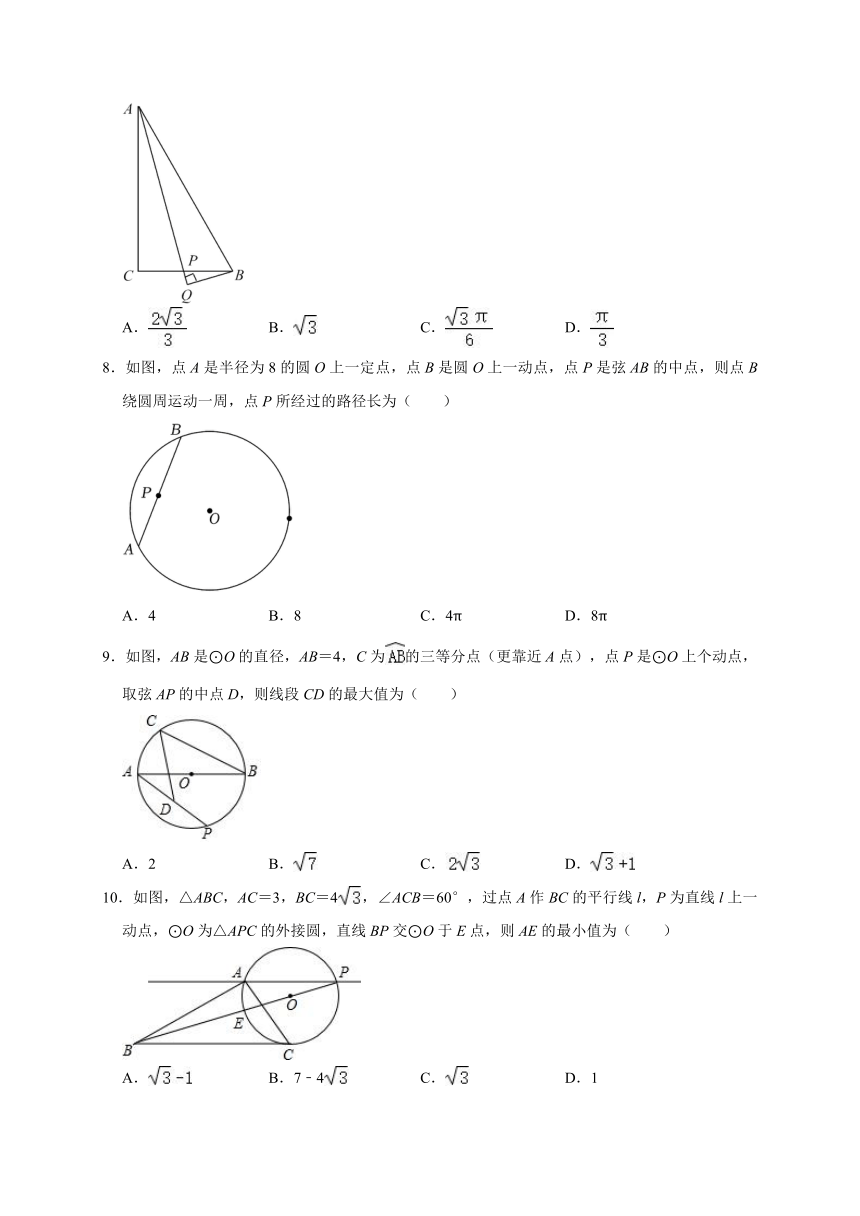
7.如图,△ABC中,∠C=90°,∠BAC=30°,AB=2,点P从C点出发,沿CB运动到点B停止,过点B作射线AP的垂线,垂足为Q,点Q运动的路径长为( )
A. B. C. D.
8.如图,点A是半径为8的圆O上一定点,点B是圆O上一动点,点P是弦AB的中点,则点B绕圆周运动一周,点P所经过的路径长为( )
A.4 B.8 C.4π D.8π
9.如图,AB是⊙O的直径,AB=4,C为的三等分点(更靠近A点),点P是⊙O上个动点,取弦AP的中点D,则线段CD的最大值为( )
A.2 B. C. D.
10.如图,△ABC,AC=3,BC=4,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为( )
A. B.7﹣4 C. D.1
二.填空题(共4小题)
11.如图,在△ABC中,AC=4,BC=9,∠ACB=60°,AM∥BC,点P在射线AM上运动,连BP交△APC的外接圆于点E,则AE的最小值为 .
12.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,点E是AC的中点,点F是斜边AB上任意一点,连接EF,将△AEF沿EF对折得到△DEF,连接DB,则△BDF周长的最小值是 .
13.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为 .
14.如图,在锐角三角形ABC中,BC=8,sinA=,BN⊥AC于点N,CM⊥AB于点M,连接MN,则△AMN面积的最大值是 .
三.解答题(共4小题)
15.阅读下列材料,并完成相应的任务.
西姆松定理是一个平面几何定理,其表述为:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线的垂线,则三垂足共线(此线常称为西姆松线). 某数学兴趣小组的同学们尝试证明该定理. 如图(1),已知△ABC内接于⊙O,点P在⊙O上(不与点A,B,C重合),过点P分别作AB,BC,AC的垂线,垂足分别为点D,E,F.求证:点D,E,F在同一条直线上. 如下是他们的证明过程(不完整): 如图(1),连接PB,PC,DE,EF,取PC的中点Q,连接QE.QF, 则EQ=FQ=PC=PQ=CQ,(依据1) ∵点E,F,P,C四点共圆, ∴∠FCP+∠FEP=180°.(依据2) 又∵∠ACP+∠ABP=180°, ∴∠FEP=∠ABP. 同上可得点B,D,P,E四点共圆, ……
任务:
(1)填空:
①依据1指的是中点的定义及 ;
②依据2指的是 .
(2)请将证明过程补充完整.
(3)善于思考的小虎发现当点P是的中点时,BD=CF,请你利用图(2)证明该结论的正确性.
16.如图,已知AB⊥MN于点B,且AB=10cm,将线段AB绕点B按逆时针方向旋转角α(0≤α≤360°)得到线段BC,过点C作CD⊥MN于点D,⊙O是△BCD的内切圆,直线AO、BC相交于点H.
(1)若α=60°,则CD= cm.
(2)若AO⊥BC
①点H与⊙O的位置关系是 ;
A.点H在⊙O外
B.点H在⊙O上
C.点H在⊙O内
②求线段AO的长度.
(3)线段AB绕点B按逆时针方向旋转90°,求点O运动的路径长.
17.如图,在平面直角坐标系中,点M在x轴负半轴上,⊙M与x轴交于A、B两点(A在B的左侧),与y轴交于C、D两点(点C在y轴正半轴上),且,点B的坐标为(3,0),点P为优弧CAD上的一个动点,连结CP,过点M作ME⊥CP于点E,交BP于点N,连结AN.
(1)求⊙M的半径长;
(2)当BP平分∠ABC时,求点P的坐标;
(3)当点P运动时,求线段AN的最小值.
18.在等腰直角△ABC中,∠ACB=90°,D是线段BC上一点,延长BC至点E,使得CE=CD,过点E作EG⊥AD于点G,交AB于点F.
(1)如图1,连接CG,若AD平分∠BAC,CG=2,求BC的长;
(2)如图2,H是平面内一点,连接AH、DH,DA平分∠EDH,∠BAH=2∠CAD,用等式表示线段BD、BF、DH之间的数量关系,并证明;
(3)如图3,在第(2)问的条件下,CD=2,AC=3,点M为平面内一点,连接BM、DM,满足∠AMD=2∠H,当BM最小时,将△BDM沿着BD翻折到同一平面内得△BDM’,过点E作EK⊥BE,交直线DM’于点K,直接写出线段EK的长度.
参考答案与试题解析
一.选择题(共10小题)
1.如图,在平面直角坐标系中,点A、B的坐标分别为(﹣3,0)、(0,4),以点A为圆心,以AB长为半径画弧交x轴上点C,则点C的坐标为( )
A.(5,0) B.(2,0)
C.(﹣8,0) D.(2,0)或(﹣8,0)
解:∵点A、B的坐标分别为(﹣3,0)、(0,4),
∴OA=3,OB=4,
∴AB==5,
∴AC′=5,AC=5,
∴C′点坐标为(2,0);C点坐标为(﹣8,0).
故选:D.
2.如图,BC是⊙O的直径,BC=4,M、N是半圆上不与B、C重合的两点,且∠MON=120°,△ABC的内心为E点,当点A在上从点M运动到点N时,点E运动的路径长是( )
A. B. C. D.
解:如图,连接BE、CE,
∵∠BAC=90°,E是内心,
∴∠BEC=135°,
∴点E在以P为圆心的PC为半径的圆上运动(轨迹是),在⊙P上取一点M′,连接BM′、CM′,则∠M′=180°﹣135°=45°,∠BPC=2∠M′=90°,
∴△BCP是等腰直角三角形,
∵BC=4,
∴PB=PC=4,
∵∠HPC=2∠HBC=∠NBC=∠NOC,同理∠GPB=∠MOB,
∴∠HPC+∠GPB=(∠NOC+∠MOB)=30°,
∴∠GPH=60°,
∴点E运动的路径长是=π,
故选:B.
3.如图,点P是正六边形ABCDEF内一点,AB=4,当∠APB=90°时,连接PD,则线段PD的最小值是( )
A. B. C.6 D.
解:∵AB=4,∠APB=90°,
∴点P在以AB为直径的圆弧上,
如图,取AB的中点O,连接OD,当O、P、D三点共线时,PD有最小值,
连接BD,过点C作CH⊥BD于点H,
∵点O为AB的中点,
∴OA=OB=OP=4÷2=2,
∵正六边形的每个内角为180°×(6﹣2)÷6=120°,
∵CD=CB,
∴∠CBD=(180°﹣120°)÷2=30°,BD=2BH,
∴∠OBD=120°﹣30°=90°,
在Rt△CBH中,CH==2,BH=,
∴BD=,
在Rt△OBD中,OD==,
∴PD的最小值为OD﹣OP=.
故选:B.
4.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
A. B.1 C. D.﹣1
解:连接AE,
∵以AD为直径的圆交BD于点E,
∴∠AED=90°,
∴点E在以AB为直径的圆O上,
连接OE,OC,
则CE≥OC﹣OE,
∵∠BAC=90°,AB=AC,
∴AC=AB=BC=2,
由勾股定理得,OC==,
∴线段CE长度的最小值为﹣1,
故选:D.
5.如图,正方形OABC中,A(8,0),B(8,8),点D坐标为(﹣6,0),连接CD,点P为边OA上一个动点,连接CP,过点D作DE⊥CP于点E,连接AE,当AE取最小值时,点E的纵坐标为( )
A.3﹣ B.4﹣ C. D.
解:∵DE⊥CP,
∴∠DEC=90°,
取CD中点F(﹣3,4),则点E的运动轨迹在以点F为圆心,半径FD=FC=FE=5的圆弧上,
连接AF,交⊙M于点E,此时AE最小,
过点F作FM⊥x轴于点M,过点E作EN⊥x轴于点N,则AM=11,FM=4,∠FMA=∠ENA=90°,
在Rt△AFM中,AF==,
∵∠FMA=∠ENA=90°,
∴FM∥EN,
∴,即,
∴EN=4﹣.
故选:B.
6.如图,在矩形ABCD中,AB=8,BC=6,点P在矩形的内部,连接PA,PB,PC,若∠PBC=∠PAB,则PC的最小值是( )
A.6 B.﹣3 C.2﹣4 D.4﹣4
解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PBC=∠PAB,
∴∠PAB+∠PBA=90°,
∴∠APB=90°,
∴点P在以AB为直径的圆上运动,设圆心为O,连接OC交⊙O于P,此时PC最小,
∵OC===2,
∴PC的最小值为2﹣4,
故选:C.
7.如图,△ABC中,∠C=90°,∠BAC=30°,AB=2,点P从C点出发,沿CB运动到点B停止,过点B作射线AP的垂线,垂足为Q,点Q运动的路径长为( )
A. B. C. D.
解:∵AQ⊥BQ,
∴点Q在以AB为直径的⊙O上运动,运动路径为,连接OC,
∵∠ACB=90°,OA=OB,
∴CO=OA=1,
∴∠COB=2∠CAB=60°,
∴的长为,
故选:D.
8.如图,点A是半径为8的圆O上一定点,点B是圆O上一动点,点P是弦AB的中点,则点B绕圆周运动一周,点P所经过的路径长为( )
A.4 B.8 C.4π D.8π
解:连接OP,OA,
∵点P为AB的中点,
∴∠OPA=90°,
∴点P在以OA为直径的圆上运动,
∵OA=8,
∴点P的运动路径长为:2π×4=8π,
故选:D.
9.如图,AB是⊙O的直径,AB=4,C为的三等分点(更靠近A点),点P是⊙O上个动点,取弦AP的中点D,则线段CD的最大值为( )
A.2 B. C. D.
解:如图,连接OD,OC,
∵AD=DP,
∴OD⊥PA,
∴∠ADO=90°,
∴点D的运动轨迹为以AO为直径的⊙K,连接CK,AC,
当点D在CK的延长线上时,CD的值最大,
∵C为的三等分点,
∴∠AOC=60°,
∴△AOC是等边三角形,
∴CK⊥OA,
在Rt△OCK中,∵∠COA=60°,OC=2,OK=1,
∴CK==,
∵DK=OA=1,
∴CD=+1,
∴CD的最大值为+1,
故选:D.
10.如图,△ABC,AC=3,BC=4,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为( )
A. B.7﹣4 C. D.1
解:如图,连接CE.
∵AP∥BC,
∴∠PAC=∠ACB=60°,
∴∠CEP=∠CAP=60°,
∴∠BEC=120°,
∴点E在以O'为圆心,O'B为半径的上运动,
连接O'A交于E′,此时AE′的值最小.此时⊙O与⊙O'交点为E'.
∵∠BE'C=120°
∴所对圆周角为60°,
∴∠BOC=2×60°=120°,
∵△BO′C是等腰三角形,BC=4,
∴O′B=O′C=4,
∵∠ACB=60°,∠BCO'=30°,
∴∠ACO'=90°
∴O'A==5,
∴AE′=O'A﹣O'E′=5﹣4=1.
故选:D.
二.填空题(共4小题)
11.如图,在△ABC中,AC=4,BC=9,∠ACB=60°,AM∥BC,点P在射线AM上运动,连BP交△APC的外接圆于点E,则AE的最小值为 2 .
解:如图,连接CE.
∵AM∥BC,
∴∠MAC=∠ACB=60°,
∴∠CEP=∠CAP=60°,
∴∠BEC=120°,
∴点E在以O为圆心,OB为半径的上运动(△BOC是等腰三角形,∠BOC=120°,OB=OC=3),连接OA交于E′,此时AE′的值最小.
∵∠ACB=60°,∠BCO=30°,
∴∠ACO=90°,
∴OA==5,
∴AE′=OA﹣OE′=5﹣3=2,
∴AE的最小值为2.
故答案为:2.
12.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,点E是AC的中点,点F是斜边AB上任意一点,连接EF,将△AEF沿EF对折得到△DEF,连接DB,则△BDF周长的最小值是 4+ .
解:在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,
∴AB=4,
∴AC===,
如图,以点E为圆心,AE为半径作圆,连接BE,交⊙E于点D′,
此时BD的长度最小,
∵将△AEF沿EF对折得到△DEF,且点E是AC的中点,
∴AF=D′F,AE=A′E=,
∵C△BD′F=D′F+FB+BD′=AF+FB+BD′=AB+BD′,
∴此时△BDF的周长最小,
过E作EM⊥AB于点M,
∴EM==,
由勾股定理可得AM===,
∴BM=AB﹣AM=,
由勾股定理可得BE===,
∴BD′=BE﹣ED′=,
∴△BDF周长的最小值是4+.
故答案为:4+.
13.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为 .
解:∵CF⊥AE,
∴∠AFC=90°,
∴点F在以AC为直径的圆上运动,
以AC为直径画半圆AC,连接OA,
当点E与B重合时,此时点F与G重合,
当点E与D重合时,此时点F与A重合,
∴点E从点B出发顺时针运动到点D时,点F所经过的路径长为的长,
∵点G为OD的中点,
∴OG=OD=OA=2,
∵OG⊥AB,
∴∠AOG=60°,AG=2,
∵OA=OC,
∴∠ACG=30°,
∴AC=2AG=4,
∴所在圆的半径为2,圆心角为60°,
∴的长为,
故答案为:.
14.如图,在锐角三角形ABC中,BC=8,sinA=,BN⊥AC于点N,CM⊥AB于点M,连接MN,则△AMN面积的最大值是 .
解:画出△ABC的外接圆⊙O,连接OB,
∵BC=8,sinA=,
∴点A在优弧BC上运动,
当A'O⊥BC时,△A'BC的面积最大,
∴BH=4,
∵∠BOH=∠BAC,
∴BO=5,OH=3,
∴AH=8,cos∠BOH=,
∴S△ABC最大为=32,
由勾股定理得,A'B=A'C=4,
∵CM⊥AB,
∴cos∠MAC=,
∴AM=,
同理AN=,
∴AM=AN,
∴△AMN∽△ABC,
∴,
∴,
∴S△AMN=,
故答案为:.
三.解答题(共4小题)
15.阅读下列材料,并完成相应的任务.
西姆松定理是一个平面几何定理,其表述为:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线的垂线,则三垂足共线(此线常称为西姆松线). 某数学兴趣小组的同学们尝试证明该定理. 如图(1),已知△ABC内接于⊙O,点P在⊙O上(不与点A,B,C重合),过点P分别作AB,BC,AC的垂线,垂足分别为点D,E,F.求证:点D,E,F在同一条直线上. 如下是他们的证明过程(不完整): 如图(1),连接PB,PC,DE,EF,取PC的中点Q,连接QE.QF, 则EQ=FQ=PC=PQ=CQ,(依据1) ∵点E,F,P,C四点共圆, ∴∠FCP+∠FEP=180°.(依据2) 又∵∠ACP+∠ABP=180°, ∴∠FEP=∠ABP. 同上可得点B,D,P,E四点共圆, ……
任务:
(1)填空:
①依据1指的是中点的定义及 直角三角形斜边上的中线等于斜边的一半 ;
②依据2指的是 圆内接四边形对角互补 .
(2)请将证明过程补充完整.
(3)善于思考的小虎发现当点P是的中点时,BD=CF,请你利用图(2)证明该结论的正确性.
(1)解:①依据1指的是中点的定义及直角三角形斜边上的中线等于斜边的一半,
②依据2指的是圆内接四边形对角互补,
故答案为:①直角三角形斜边上的中线等于斜边的一半;②圆内接四边形对角互补;
(2)解:如图(1),连接PB,PC,DE,EF,取PC的中点Q,连接QE.QF,
则EQ=FQ=PC=PQ=CQ,
∴点E,F,P,C四点共圆,
∴∠FCP+∠FEP=180°,
又∵∠ACP+∠ABP=180°,
∴∠FEP=∠ABP,
同上可得点B,D,P,E四点共圆,
∴∠DBP=∠DEP,
∵∠ABP+∠DBP=180°,
∴∠FEP+∠DEP=180°,
∴点D,E,F在同一直线上;
(3)证明:如图,连接PA,PB,PC,
∵点P是的中点,
∴,
∴BP=PC,∠PAD=∠PAC,
又∵PD⊥AD,PF⊥AC,
∴PD=PF,
∴Rt△PBD≌Rt△PCF(HL),
∴BD=CF.
16.如图,已知AB⊥MN于点B,且AB=10cm,将线段AB绕点B按逆时针方向旋转角α(0≤α≤360°)得到线段BC,过点C作CD⊥MN于点D,⊙O是△BCD的内切圆,直线AO、BC相交于点H.
(1)若α=60°,则CD= 5 cm.
(2)若AO⊥BC
①点H与⊙O的位置关系是 B ;
A.点H在⊙O外
B.点H在⊙O上
C.点H在⊙O内
②求线段AO的长度.
(3)线段AB绕点B按逆时针方向旋转90°,求点O运动的路径长.
解:(1)∵线段AB绕点B按逆时针方向旋转角α(0≤α≤360°)得到线段BC,
∴BC=BA=10cm,
当α=60°时,∠CBD=30°,
∴CD=BC=5cm,
故答案为:5;
(2)①当AO⊥BC时,
则OH⊥BC,
若⊙O与BC相切于P,
则OP⊥BC,
∴点P与H重合,
∴点H在⊙O上,
故选:B;
②延长AO交BD于E,
∵AO⊥BC,
∴∠A=∠CBD=90°﹣α,
∵⊙O是△BCD的内切圆,
∴BO平分∠CBD,
∴∠OBC=∠CBD=45°﹣α,
∴∠AOB=90°﹣∠OBC=90°﹣(45°﹣α)=45°+α,
∵∠ABO=∠ABC+∠CBO=α+45°﹣α=45°+α,
∴∠AOB=∠ABO,
∴AO=AB=10cm;
(3)如图,在直线BD上取BG=BC,连接OG,以BG为斜边在等腰直角△BFG,
∵∠OBG=∠OBC,OB=OB,
∴△BOG≌△BOC(SAS),
∴∠BOC=∠BOG,
∵∠BCD+∠CBD=90°,
∴∠BCO+∠OBC=45°,
∴∠BOC=135°,
∴∠BOG=135°,
∴点O在以F为圆心、BF为半径的圆上运动,
∵BG=BC=10cm,
∴BF=5cm,
∴当线段AB绕点B按逆时针方向旋转90°时,O运动的路径长为=(cm).
17.如图,在平面直角坐标系中,点M在x轴负半轴上,⊙M与x轴交于A、B两点(A在B的左侧),与y轴交于C、D两点(点C在y轴正半轴上),且,点B的坐标为(3,0),点P为优弧CAD上的一个动点,连结CP,过点M作ME⊥CP于点E,交BP于点N,连结AN.
(1)求⊙M的半径长;
(2)当BP平分∠ABC时,求点P的坐标;
(3)当点P运动时,求线段AN的最小值.
解:(1)如图,连接CM,
∵CD=2OM,
∴OM,
∵CD⊥MB,
∴CM==2OM,
∴∠MCO=30°,∠CMO=60°,
∵MC=MB,
∴△CMB为等边三角形,
∵B(3,0),
∴OB=3,
∴MB=2OB=6,
∴⊙M的半径长为6;
(2)连接AP,过点P作PF⊥AB于F,
∵AB为⊙M的直径,AB=2MB=12,
∴∠APB=90°,
∴△APB为直角三角形,
由(1)得△CMB是等边三角形,
∵BP平分∠ABC,
∴∠ABP=30°,
∴AP=,
∴BP==6,
在Rt△PFB中,由∠ABP=30°,
∴PF=,
∴BF==9,
∴OF=BF﹣OB=6,
∴OF=6,PF=3,
∴P(﹣6,3);
(3)∵CD垂直平分MB,
∴在OC上取点G,使∠GMB=30°,连接GM,GB,
∵ME⊥PC,
∴∠PEM=90°,
∵∠CPB=∠CMB=30°,
∴∠PNE=∠BNM=60°,
∴BM=6,
∴点N在以G为圆心,GM为半径的圆上,连接AG,此时AN的最小值为AG﹣GM,
∵BM=6,∠GMB=30°,
∴OG=,GM=2,
在Rt△AOG中,由勾股定理得,AG=,
∴AN的最小值为2﹣2.
18.在等腰直角△ABC中,∠ACB=90°,D是线段BC上一点,延长BC至点E,使得CE=CD,过点E作EG⊥AD于点G,交AB于点F.
(1)如图1,连接CG,若AD平分∠BAC,CG=2,求BC的长;
(2)如图2,H是平面内一点,连接AH、DH,DA平分∠EDH,∠BAH=2∠CAD,用等式表示线段BD、BF、DH之间的数量关系,并证明;
(3)如图3,在第(2)问的条件下,CD=2,AC=3,点M为平面内一点,连接BM、DM,满足∠AMD=2∠H,当BM最小时,将△BDM沿着BD翻折到同一平面内得△BDM’,过点E作EK⊥BE,交直线DM’于点K,直接写出线段EK的长度.
解:(1)如图1,过点D作DQ⊥AB于Q,
∵AD平分∠BAC,DC⊥AC,DQ⊥AB,
∴DQ=DC=2,
∵△ABC是等腰直角三角形,
∴∠B=∠BAC=45°,
∵∠BQD=90,
∴△BDQ是等腰直角三角形,
∴BD=DQ=2,
∴BC=BD+DC=2+2;
(2)BD+BF=DH;理由如下:
如图2,在线段HD上取点N,连接AN,使∠HAN=∠BAD,过点F作FT⊥BC于T,连接AE,
∵CE=CD,∠ACE=∠ACB=90°,AC=AC,
∴△ACE≌△ACD(SAS),
∴∠AEC=∠ADC,∠CAE=∠CAD,AE=AD,
∴∠DAE=2∠CAD,
∵EG⊥AD,
∴∠FET+∠ADC=90°,
∵∠CAD+∠ADC=90°,
∴∠FET=∠CAD,
∵∠AFE=∠FET+∠B=∠CAD+45°,∠EAF=∠CAE+∠BAC=∠CAD+45°,
∴∠AFE=∠EAF,
∴AE=EF=AD,
在△CAD和△TEF中,
,
∴△CAD≌△TEF(AAS),
∴FT=CD=DE,∠ADE=∠AED,
∵△BET是等腰直角三角形,
∴BF=FT=DE,
∴DE=BF,
∵DA平分∠EDH,
∴∠ADH=∠ADE=∠AED,
∵∠ADE+∠AED+∠DAE=180°,∠ADE+∠ADH+∠BDH=180°,
∴∠DAE=∠BDH,
∵∠BAH=2∠CAD,
∴∠BAH=∠BDH,
∵∠BAH+∠H=∠BDH+∠B,
∴∠H=∠B=45°,
∵∠AND=∠HAN+∠H=∠BAD+45°=∠ADE=∠ADH,
∴AN=AD,
∴AN=AE,
在△AHN和△ABD中,
,
∴△AHN≌△ABD(AAS),
∴HN=BD,
∵∠DAH=∠BAD+∠BAH=∠NAN+∠DAN,
∴∠DAN=∠BAH=∠DAE,
在△ADN和△ADE中,
,
∴△ADN≌△ADE(SAS),
∴DN=DE,
∴DN=BF,
∵HN+DN=DH,
∴BD+BF=DH;
(3)由(2)知∠H=45°,
如图3,以AD为直径作⊙O,
∵∠AMD=2∠H,
∴∠AMD=90°,
∴点M在⊙O上,
∴当BM最小时,点M为线段OB与⊙O的交点,
如图4,连接OB交⊙O于M,作点M关于BD的对称点M′,连接MM′交BD于L,过点O作OP⊥BC于P,
则OP=AC=,PD=CD=1,BD=BC﹣CD=1,
∴BP=2,
在Rt△ACD中,AD==,
∴OM=,
在Rt△BOP中,OB===,
∴BM=OB﹣OM=﹣=,
∵M与M′关于BD对称,
∴MM′⊥BD,ML=M′L,
∵∠BLM=∠BPO=90°,∠MBL=∠OBP,
∴△BML∽△BOP,
∴==,即==,
∴ML=,BL=,
∴M′L=,DL=BD﹣BL=1﹣=,
∵EK⊥BE,
∴∠DEK=∠DLM′=90°,
∵∠EDK=∠M′DL,
∴△DEK∽△DLM′,
∴=,
∵DE=2CD=4,
∴=,
∴EK=.
内容提要
隐圆模型
(1)动点到定点定长模型
(2)直角圆周角模型
(3)定边对定角模型
(4)四点共圆模型①
(5)四点共圆模型②
知识点拓展详解
隐圆模型
(1)动点到定点定长模型(共顶点的三条等线段)
若P为动点,但AB=AC=AP 原理:圆A中,AB=AC=AP
则B、C、P三点共圆,A圆心,AB半径 备注:常转全等或相似证明出定长
(2)直角圆周角模型
固定线段AB所对动角∠C恒为90° 原理:圆O中,圆周角为90°所对弦是直径
则A、B、C三点共圆,AB为直径 备注:常通过互余转换等证明出动角恒为直角
(3)定边对定角模型
固定线段AB所对动角∠P为定值 原理:弦AB所对同侧圆周角恒相等
则点P运动轨迹为过A、B、C三点的圆 备注:点P在优弧、劣弧上运动皆可
(4)四点共圆模型①
若动角∠A+动角∠C=180° 原理:圆内接四边形对角互补
则A、B、C、D四点共圆 备注:点A与点C在线段AB异侧
(5)四点共圆模型②
固定线段AB所对同侧动角∠P=∠C 原理:弦AB所对同侧圆周角恒相等
则A、B、C、P四点共圆 备注:点P与点C需在线段AB同侧
强化同步练习
一.选择题(共10小题)
1.如图,在平面直角坐标系中,点A、B的坐标分别为(﹣3,0)、(0,4),以点A为圆心,以AB长为半径画弧交x轴上点C,则点C的坐标为( )
A.(5,0) B.(2,0)
C.(﹣8,0) D.(2,0)或(﹣8,0)
2.如图,BC是⊙O的直径,BC=4,M、N是半圆上不与B、C重合的两点,且∠MON=120°,△ABC的内心为E点,当点A在上从点M运动到点N时,点E运动的路径长是( )
A. B. C. D.
3.如图,点P是正六边形ABCDEF内一点,AB=4,当∠APB=90°时,连接PD,则线段PD的最小值是( )
A. B. C.6 D.
4.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
A. B.1 C. D.﹣1
5.如图,正方形OABC中,A(8,0),B(8,8),点D坐标为(﹣6,0),连接CD,点P为边OA上一个动点,连接CP,过点D作DE⊥CP于点E,连接AE,当AE取最小值时,点E的纵坐标为( )
A.3﹣ B.4﹣ C. D.
6.如图,在矩形ABCD中,AB=8,BC=6,点P在矩形的内部,连接PA,PB,PC,若∠PBC=∠PAB,则PC的最小值是( )
A.6 B.﹣3 C.2﹣4 D.4﹣4
7.如图,△ABC中,∠C=90°,∠BAC=30°,AB=2,点P从C点出发,沿CB运动到点B停止,过点B作射线AP的垂线,垂足为Q,点Q运动的路径长为( )
A. B. C. D.
8.如图,点A是半径为8的圆O上一定点,点B是圆O上一动点,点P是弦AB的中点,则点B绕圆周运动一周,点P所经过的路径长为( )
A.4 B.8 C.4π D.8π
9.如图,AB是⊙O的直径,AB=4,C为的三等分点(更靠近A点),点P是⊙O上个动点,取弦AP的中点D,则线段CD的最大值为( )
A.2 B. C. D.
10.如图,△ABC,AC=3,BC=4,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为( )
A. B.7﹣4 C. D.1
二.填空题(共4小题)
11.如图,在△ABC中,AC=4,BC=9,∠ACB=60°,AM∥BC,点P在射线AM上运动,连BP交△APC的外接圆于点E,则AE的最小值为 .
12.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,点E是AC的中点,点F是斜边AB上任意一点,连接EF,将△AEF沿EF对折得到△DEF,连接DB,则△BDF周长的最小值是 .
13.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为 .
14.如图,在锐角三角形ABC中,BC=8,sinA=,BN⊥AC于点N,CM⊥AB于点M,连接MN,则△AMN面积的最大值是 .
三.解答题(共4小题)
15.阅读下列材料,并完成相应的任务.
西姆松定理是一个平面几何定理,其表述为:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线的垂线,则三垂足共线(此线常称为西姆松线). 某数学兴趣小组的同学们尝试证明该定理. 如图(1),已知△ABC内接于⊙O,点P在⊙O上(不与点A,B,C重合),过点P分别作AB,BC,AC的垂线,垂足分别为点D,E,F.求证:点D,E,F在同一条直线上. 如下是他们的证明过程(不完整): 如图(1),连接PB,PC,DE,EF,取PC的中点Q,连接QE.QF, 则EQ=FQ=PC=PQ=CQ,(依据1) ∵点E,F,P,C四点共圆, ∴∠FCP+∠FEP=180°.(依据2) 又∵∠ACP+∠ABP=180°, ∴∠FEP=∠ABP. 同上可得点B,D,P,E四点共圆, ……
任务:
(1)填空:
①依据1指的是中点的定义及 ;
②依据2指的是 .
(2)请将证明过程补充完整.
(3)善于思考的小虎发现当点P是的中点时,BD=CF,请你利用图(2)证明该结论的正确性.
16.如图,已知AB⊥MN于点B,且AB=10cm,将线段AB绕点B按逆时针方向旋转角α(0≤α≤360°)得到线段BC,过点C作CD⊥MN于点D,⊙O是△BCD的内切圆,直线AO、BC相交于点H.
(1)若α=60°,则CD= cm.
(2)若AO⊥BC
①点H与⊙O的位置关系是 ;
A.点H在⊙O外
B.点H在⊙O上
C.点H在⊙O内
②求线段AO的长度.
(3)线段AB绕点B按逆时针方向旋转90°,求点O运动的路径长.
17.如图,在平面直角坐标系中,点M在x轴负半轴上,⊙M与x轴交于A、B两点(A在B的左侧),与y轴交于C、D两点(点C在y轴正半轴上),且,点B的坐标为(3,0),点P为优弧CAD上的一个动点,连结CP,过点M作ME⊥CP于点E,交BP于点N,连结AN.
(1)求⊙M的半径长;
(2)当BP平分∠ABC时,求点P的坐标;
(3)当点P运动时,求线段AN的最小值.
18.在等腰直角△ABC中,∠ACB=90°,D是线段BC上一点,延长BC至点E,使得CE=CD,过点E作EG⊥AD于点G,交AB于点F.
(1)如图1,连接CG,若AD平分∠BAC,CG=2,求BC的长;
(2)如图2,H是平面内一点,连接AH、DH,DA平分∠EDH,∠BAH=2∠CAD,用等式表示线段BD、BF、DH之间的数量关系,并证明;
(3)如图3,在第(2)问的条件下,CD=2,AC=3,点M为平面内一点,连接BM、DM,满足∠AMD=2∠H,当BM最小时,将△BDM沿着BD翻折到同一平面内得△BDM’,过点E作EK⊥BE,交直线DM’于点K,直接写出线段EK的长度.
参考答案与试题解析
一.选择题(共10小题)
1.如图,在平面直角坐标系中,点A、B的坐标分别为(﹣3,0)、(0,4),以点A为圆心,以AB长为半径画弧交x轴上点C,则点C的坐标为( )
A.(5,0) B.(2,0)
C.(﹣8,0) D.(2,0)或(﹣8,0)
解:∵点A、B的坐标分别为(﹣3,0)、(0,4),
∴OA=3,OB=4,
∴AB==5,
∴AC′=5,AC=5,
∴C′点坐标为(2,0);C点坐标为(﹣8,0).
故选:D.
2.如图,BC是⊙O的直径,BC=4,M、N是半圆上不与B、C重合的两点,且∠MON=120°,△ABC的内心为E点,当点A在上从点M运动到点N时,点E运动的路径长是( )
A. B. C. D.
解:如图,连接BE、CE,
∵∠BAC=90°,E是内心,
∴∠BEC=135°,
∴点E在以P为圆心的PC为半径的圆上运动(轨迹是),在⊙P上取一点M′,连接BM′、CM′,则∠M′=180°﹣135°=45°,∠BPC=2∠M′=90°,
∴△BCP是等腰直角三角形,
∵BC=4,
∴PB=PC=4,
∵∠HPC=2∠HBC=∠NBC=∠NOC,同理∠GPB=∠MOB,
∴∠HPC+∠GPB=(∠NOC+∠MOB)=30°,
∴∠GPH=60°,
∴点E运动的路径长是=π,
故选:B.
3.如图,点P是正六边形ABCDEF内一点,AB=4,当∠APB=90°时,连接PD,则线段PD的最小值是( )
A. B. C.6 D.
解:∵AB=4,∠APB=90°,
∴点P在以AB为直径的圆弧上,
如图,取AB的中点O,连接OD,当O、P、D三点共线时,PD有最小值,
连接BD,过点C作CH⊥BD于点H,
∵点O为AB的中点,
∴OA=OB=OP=4÷2=2,
∵正六边形的每个内角为180°×(6﹣2)÷6=120°,
∵CD=CB,
∴∠CBD=(180°﹣120°)÷2=30°,BD=2BH,
∴∠OBD=120°﹣30°=90°,
在Rt△CBH中,CH==2,BH=,
∴BD=,
在Rt△OBD中,OD==,
∴PD的最小值为OD﹣OP=.
故选:B.
4.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
A. B.1 C. D.﹣1
解:连接AE,
∵以AD为直径的圆交BD于点E,
∴∠AED=90°,
∴点E在以AB为直径的圆O上,
连接OE,OC,
则CE≥OC﹣OE,
∵∠BAC=90°,AB=AC,
∴AC=AB=BC=2,
由勾股定理得,OC==,
∴线段CE长度的最小值为﹣1,
故选:D.
5.如图,正方形OABC中,A(8,0),B(8,8),点D坐标为(﹣6,0),连接CD,点P为边OA上一个动点,连接CP,过点D作DE⊥CP于点E,连接AE,当AE取最小值时,点E的纵坐标为( )
A.3﹣ B.4﹣ C. D.
解:∵DE⊥CP,
∴∠DEC=90°,
取CD中点F(﹣3,4),则点E的运动轨迹在以点F为圆心,半径FD=FC=FE=5的圆弧上,
连接AF,交⊙M于点E,此时AE最小,
过点F作FM⊥x轴于点M,过点E作EN⊥x轴于点N,则AM=11,FM=4,∠FMA=∠ENA=90°,
在Rt△AFM中,AF==,
∵∠FMA=∠ENA=90°,
∴FM∥EN,
∴,即,
∴EN=4﹣.
故选:B.
6.如图,在矩形ABCD中,AB=8,BC=6,点P在矩形的内部,连接PA,PB,PC,若∠PBC=∠PAB,则PC的最小值是( )
A.6 B.﹣3 C.2﹣4 D.4﹣4
解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PBC=∠PAB,
∴∠PAB+∠PBA=90°,
∴∠APB=90°,
∴点P在以AB为直径的圆上运动,设圆心为O,连接OC交⊙O于P,此时PC最小,
∵OC===2,
∴PC的最小值为2﹣4,
故选:C.
7.如图,△ABC中,∠C=90°,∠BAC=30°,AB=2,点P从C点出发,沿CB运动到点B停止,过点B作射线AP的垂线,垂足为Q,点Q运动的路径长为( )
A. B. C. D.
解:∵AQ⊥BQ,
∴点Q在以AB为直径的⊙O上运动,运动路径为,连接OC,
∵∠ACB=90°,OA=OB,
∴CO=OA=1,
∴∠COB=2∠CAB=60°,
∴的长为,
故选:D.
8.如图,点A是半径为8的圆O上一定点,点B是圆O上一动点,点P是弦AB的中点,则点B绕圆周运动一周,点P所经过的路径长为( )
A.4 B.8 C.4π D.8π
解:连接OP,OA,
∵点P为AB的中点,
∴∠OPA=90°,
∴点P在以OA为直径的圆上运动,
∵OA=8,
∴点P的运动路径长为:2π×4=8π,
故选:D.
9.如图,AB是⊙O的直径,AB=4,C为的三等分点(更靠近A点),点P是⊙O上个动点,取弦AP的中点D,则线段CD的最大值为( )
A.2 B. C. D.
解:如图,连接OD,OC,
∵AD=DP,
∴OD⊥PA,
∴∠ADO=90°,
∴点D的运动轨迹为以AO为直径的⊙K,连接CK,AC,
当点D在CK的延长线上时,CD的值最大,
∵C为的三等分点,
∴∠AOC=60°,
∴△AOC是等边三角形,
∴CK⊥OA,
在Rt△OCK中,∵∠COA=60°,OC=2,OK=1,
∴CK==,
∵DK=OA=1,
∴CD=+1,
∴CD的最大值为+1,
故选:D.
10.如图,△ABC,AC=3,BC=4,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为( )
A. B.7﹣4 C. D.1
解:如图,连接CE.
∵AP∥BC,
∴∠PAC=∠ACB=60°,
∴∠CEP=∠CAP=60°,
∴∠BEC=120°,
∴点E在以O'为圆心,O'B为半径的上运动,
连接O'A交于E′,此时AE′的值最小.此时⊙O与⊙O'交点为E'.
∵∠BE'C=120°
∴所对圆周角为60°,
∴∠BOC=2×60°=120°,
∵△BO′C是等腰三角形,BC=4,
∴O′B=O′C=4,
∵∠ACB=60°,∠BCO'=30°,
∴∠ACO'=90°
∴O'A==5,
∴AE′=O'A﹣O'E′=5﹣4=1.
故选:D.
二.填空题(共4小题)
11.如图,在△ABC中,AC=4,BC=9,∠ACB=60°,AM∥BC,点P在射线AM上运动,连BP交△APC的外接圆于点E,则AE的最小值为 2 .
解:如图,连接CE.
∵AM∥BC,
∴∠MAC=∠ACB=60°,
∴∠CEP=∠CAP=60°,
∴∠BEC=120°,
∴点E在以O为圆心,OB为半径的上运动(△BOC是等腰三角形,∠BOC=120°,OB=OC=3),连接OA交于E′,此时AE′的值最小.
∵∠ACB=60°,∠BCO=30°,
∴∠ACO=90°,
∴OA==5,
∴AE′=OA﹣OE′=5﹣3=2,
∴AE的最小值为2.
故答案为:2.
12.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,点E是AC的中点,点F是斜边AB上任意一点,连接EF,将△AEF沿EF对折得到△DEF,连接DB,则△BDF周长的最小值是 4+ .
解:在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,
∴AB=4,
∴AC===,
如图,以点E为圆心,AE为半径作圆,连接BE,交⊙E于点D′,
此时BD的长度最小,
∵将△AEF沿EF对折得到△DEF,且点E是AC的中点,
∴AF=D′F,AE=A′E=,
∵C△BD′F=D′F+FB+BD′=AF+FB+BD′=AB+BD′,
∴此时△BDF的周长最小,
过E作EM⊥AB于点M,
∴EM==,
由勾股定理可得AM===,
∴BM=AB﹣AM=,
由勾股定理可得BE===,
∴BD′=BE﹣ED′=,
∴△BDF周长的最小值是4+.
故答案为:4+.
13.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为 .
解:∵CF⊥AE,
∴∠AFC=90°,
∴点F在以AC为直径的圆上运动,
以AC为直径画半圆AC,连接OA,
当点E与B重合时,此时点F与G重合,
当点E与D重合时,此时点F与A重合,
∴点E从点B出发顺时针运动到点D时,点F所经过的路径长为的长,
∵点G为OD的中点,
∴OG=OD=OA=2,
∵OG⊥AB,
∴∠AOG=60°,AG=2,
∵OA=OC,
∴∠ACG=30°,
∴AC=2AG=4,
∴所在圆的半径为2,圆心角为60°,
∴的长为,
故答案为:.
14.如图,在锐角三角形ABC中,BC=8,sinA=,BN⊥AC于点N,CM⊥AB于点M,连接MN,则△AMN面积的最大值是 .
解:画出△ABC的外接圆⊙O,连接OB,
∵BC=8,sinA=,
∴点A在优弧BC上运动,
当A'O⊥BC时,△A'BC的面积最大,
∴BH=4,
∵∠BOH=∠BAC,
∴BO=5,OH=3,
∴AH=8,cos∠BOH=,
∴S△ABC最大为=32,
由勾股定理得,A'B=A'C=4,
∵CM⊥AB,
∴cos∠MAC=,
∴AM=,
同理AN=,
∴AM=AN,
∴△AMN∽△ABC,
∴,
∴,
∴S△AMN=,
故答案为:.
三.解答题(共4小题)
15.阅读下列材料,并完成相应的任务.
西姆松定理是一个平面几何定理,其表述为:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线的垂线,则三垂足共线(此线常称为西姆松线). 某数学兴趣小组的同学们尝试证明该定理. 如图(1),已知△ABC内接于⊙O,点P在⊙O上(不与点A,B,C重合),过点P分别作AB,BC,AC的垂线,垂足分别为点D,E,F.求证:点D,E,F在同一条直线上. 如下是他们的证明过程(不完整): 如图(1),连接PB,PC,DE,EF,取PC的中点Q,连接QE.QF, 则EQ=FQ=PC=PQ=CQ,(依据1) ∵点E,F,P,C四点共圆, ∴∠FCP+∠FEP=180°.(依据2) 又∵∠ACP+∠ABP=180°, ∴∠FEP=∠ABP. 同上可得点B,D,P,E四点共圆, ……
任务:
(1)填空:
①依据1指的是中点的定义及 直角三角形斜边上的中线等于斜边的一半 ;
②依据2指的是 圆内接四边形对角互补 .
(2)请将证明过程补充完整.
(3)善于思考的小虎发现当点P是的中点时,BD=CF,请你利用图(2)证明该结论的正确性.
(1)解:①依据1指的是中点的定义及直角三角形斜边上的中线等于斜边的一半,
②依据2指的是圆内接四边形对角互补,
故答案为:①直角三角形斜边上的中线等于斜边的一半;②圆内接四边形对角互补;
(2)解:如图(1),连接PB,PC,DE,EF,取PC的中点Q,连接QE.QF,
则EQ=FQ=PC=PQ=CQ,
∴点E,F,P,C四点共圆,
∴∠FCP+∠FEP=180°,
又∵∠ACP+∠ABP=180°,
∴∠FEP=∠ABP,
同上可得点B,D,P,E四点共圆,
∴∠DBP=∠DEP,
∵∠ABP+∠DBP=180°,
∴∠FEP+∠DEP=180°,
∴点D,E,F在同一直线上;
(3)证明:如图,连接PA,PB,PC,
∵点P是的中点,
∴,
∴BP=PC,∠PAD=∠PAC,
又∵PD⊥AD,PF⊥AC,
∴PD=PF,
∴Rt△PBD≌Rt△PCF(HL),
∴BD=CF.
16.如图,已知AB⊥MN于点B,且AB=10cm,将线段AB绕点B按逆时针方向旋转角α(0≤α≤360°)得到线段BC,过点C作CD⊥MN于点D,⊙O是△BCD的内切圆,直线AO、BC相交于点H.
(1)若α=60°,则CD= 5 cm.
(2)若AO⊥BC
①点H与⊙O的位置关系是 B ;
A.点H在⊙O外
B.点H在⊙O上
C.点H在⊙O内
②求线段AO的长度.
(3)线段AB绕点B按逆时针方向旋转90°,求点O运动的路径长.
解:(1)∵线段AB绕点B按逆时针方向旋转角α(0≤α≤360°)得到线段BC,
∴BC=BA=10cm,
当α=60°时,∠CBD=30°,
∴CD=BC=5cm,
故答案为:5;
(2)①当AO⊥BC时,
则OH⊥BC,
若⊙O与BC相切于P,
则OP⊥BC,
∴点P与H重合,
∴点H在⊙O上,
故选:B;
②延长AO交BD于E,
∵AO⊥BC,
∴∠A=∠CBD=90°﹣α,
∵⊙O是△BCD的内切圆,
∴BO平分∠CBD,
∴∠OBC=∠CBD=45°﹣α,
∴∠AOB=90°﹣∠OBC=90°﹣(45°﹣α)=45°+α,
∵∠ABO=∠ABC+∠CBO=α+45°﹣α=45°+α,
∴∠AOB=∠ABO,
∴AO=AB=10cm;
(3)如图,在直线BD上取BG=BC,连接OG,以BG为斜边在等腰直角△BFG,
∵∠OBG=∠OBC,OB=OB,
∴△BOG≌△BOC(SAS),
∴∠BOC=∠BOG,
∵∠BCD+∠CBD=90°,
∴∠BCO+∠OBC=45°,
∴∠BOC=135°,
∴∠BOG=135°,
∴点O在以F为圆心、BF为半径的圆上运动,
∵BG=BC=10cm,
∴BF=5cm,
∴当线段AB绕点B按逆时针方向旋转90°时,O运动的路径长为=(cm).
17.如图,在平面直角坐标系中,点M在x轴负半轴上,⊙M与x轴交于A、B两点(A在B的左侧),与y轴交于C、D两点(点C在y轴正半轴上),且,点B的坐标为(3,0),点P为优弧CAD上的一个动点,连结CP,过点M作ME⊥CP于点E,交BP于点N,连结AN.
(1)求⊙M的半径长;
(2)当BP平分∠ABC时,求点P的坐标;
(3)当点P运动时,求线段AN的最小值.
解:(1)如图,连接CM,
∵CD=2OM,
∴OM,
∵CD⊥MB,
∴CM==2OM,
∴∠MCO=30°,∠CMO=60°,
∵MC=MB,
∴△CMB为等边三角形,
∵B(3,0),
∴OB=3,
∴MB=2OB=6,
∴⊙M的半径长为6;
(2)连接AP,过点P作PF⊥AB于F,
∵AB为⊙M的直径,AB=2MB=12,
∴∠APB=90°,
∴△APB为直角三角形,
由(1)得△CMB是等边三角形,
∵BP平分∠ABC,
∴∠ABP=30°,
∴AP=,
∴BP==6,
在Rt△PFB中,由∠ABP=30°,
∴PF=,
∴BF==9,
∴OF=BF﹣OB=6,
∴OF=6,PF=3,
∴P(﹣6,3);
(3)∵CD垂直平分MB,
∴在OC上取点G,使∠GMB=30°,连接GM,GB,
∵ME⊥PC,
∴∠PEM=90°,
∵∠CPB=∠CMB=30°,
∴∠PNE=∠BNM=60°,
∴BM=6,
∴点N在以G为圆心,GM为半径的圆上,连接AG,此时AN的最小值为AG﹣GM,
∵BM=6,∠GMB=30°,
∴OG=,GM=2,
在Rt△AOG中,由勾股定理得,AG=,
∴AN的最小值为2﹣2.
18.在等腰直角△ABC中,∠ACB=90°,D是线段BC上一点,延长BC至点E,使得CE=CD,过点E作EG⊥AD于点G,交AB于点F.
(1)如图1,连接CG,若AD平分∠BAC,CG=2,求BC的长;
(2)如图2,H是平面内一点,连接AH、DH,DA平分∠EDH,∠BAH=2∠CAD,用等式表示线段BD、BF、DH之间的数量关系,并证明;
(3)如图3,在第(2)问的条件下,CD=2,AC=3,点M为平面内一点,连接BM、DM,满足∠AMD=2∠H,当BM最小时,将△BDM沿着BD翻折到同一平面内得△BDM’,过点E作EK⊥BE,交直线DM’于点K,直接写出线段EK的长度.
解:(1)如图1,过点D作DQ⊥AB于Q,
∵AD平分∠BAC,DC⊥AC,DQ⊥AB,
∴DQ=DC=2,
∵△ABC是等腰直角三角形,
∴∠B=∠BAC=45°,
∵∠BQD=90,
∴△BDQ是等腰直角三角形,
∴BD=DQ=2,
∴BC=BD+DC=2+2;
(2)BD+BF=DH;理由如下:
如图2,在线段HD上取点N,连接AN,使∠HAN=∠BAD,过点F作FT⊥BC于T,连接AE,
∵CE=CD,∠ACE=∠ACB=90°,AC=AC,
∴△ACE≌△ACD(SAS),
∴∠AEC=∠ADC,∠CAE=∠CAD,AE=AD,
∴∠DAE=2∠CAD,
∵EG⊥AD,
∴∠FET+∠ADC=90°,
∵∠CAD+∠ADC=90°,
∴∠FET=∠CAD,
∵∠AFE=∠FET+∠B=∠CAD+45°,∠EAF=∠CAE+∠BAC=∠CAD+45°,
∴∠AFE=∠EAF,
∴AE=EF=AD,
在△CAD和△TEF中,
,
∴△CAD≌△TEF(AAS),
∴FT=CD=DE,∠ADE=∠AED,
∵△BET是等腰直角三角形,
∴BF=FT=DE,
∴DE=BF,
∵DA平分∠EDH,
∴∠ADH=∠ADE=∠AED,
∵∠ADE+∠AED+∠DAE=180°,∠ADE+∠ADH+∠BDH=180°,
∴∠DAE=∠BDH,
∵∠BAH=2∠CAD,
∴∠BAH=∠BDH,
∵∠BAH+∠H=∠BDH+∠B,
∴∠H=∠B=45°,
∵∠AND=∠HAN+∠H=∠BAD+45°=∠ADE=∠ADH,
∴AN=AD,
∴AN=AE,
在△AHN和△ABD中,
,
∴△AHN≌△ABD(AAS),
∴HN=BD,
∵∠DAH=∠BAD+∠BAH=∠NAN+∠DAN,
∴∠DAN=∠BAH=∠DAE,
在△ADN和△ADE中,
,
∴△ADN≌△ADE(SAS),
∴DN=DE,
∴DN=BF,
∵HN+DN=DH,
∴BD+BF=DH;
(3)由(2)知∠H=45°,
如图3,以AD为直径作⊙O,
∵∠AMD=2∠H,
∴∠AMD=90°,
∴点M在⊙O上,
∴当BM最小时,点M为线段OB与⊙O的交点,
如图4,连接OB交⊙O于M,作点M关于BD的对称点M′,连接MM′交BD于L,过点O作OP⊥BC于P,
则OP=AC=,PD=CD=1,BD=BC﹣CD=1,
∴BP=2,
在Rt△ACD中,AD==,
∴OM=,
在Rt△BOP中,OB===,
∴BM=OB﹣OM=﹣=,
∵M与M′关于BD对称,
∴MM′⊥BD,ML=M′L,
∵∠BLM=∠BPO=90°,∠MBL=∠OBP,
∴△BML∽△BOP,
∴==,即==,
∴ML=,BL=,
∴M′L=,DL=BD﹣BL=1﹣=,
∵EK⊥BE,
∴∠DEK=∠DLM′=90°,
∵∠EDK=∠M′DL,
∴△DEK∽△DLM′,
∴=,
∵DE=2CD=4,
∴=,
∴EK=.
同课章节目录
