2023年中考数学复习 第九讲函数与面积定值最值问题专题(压轴题专题讲义)(含答案)
文档属性
| 名称 | 2023年中考数学复习 第九讲函数与面积定值最值问题专题(压轴题专题讲义)(含答案) | 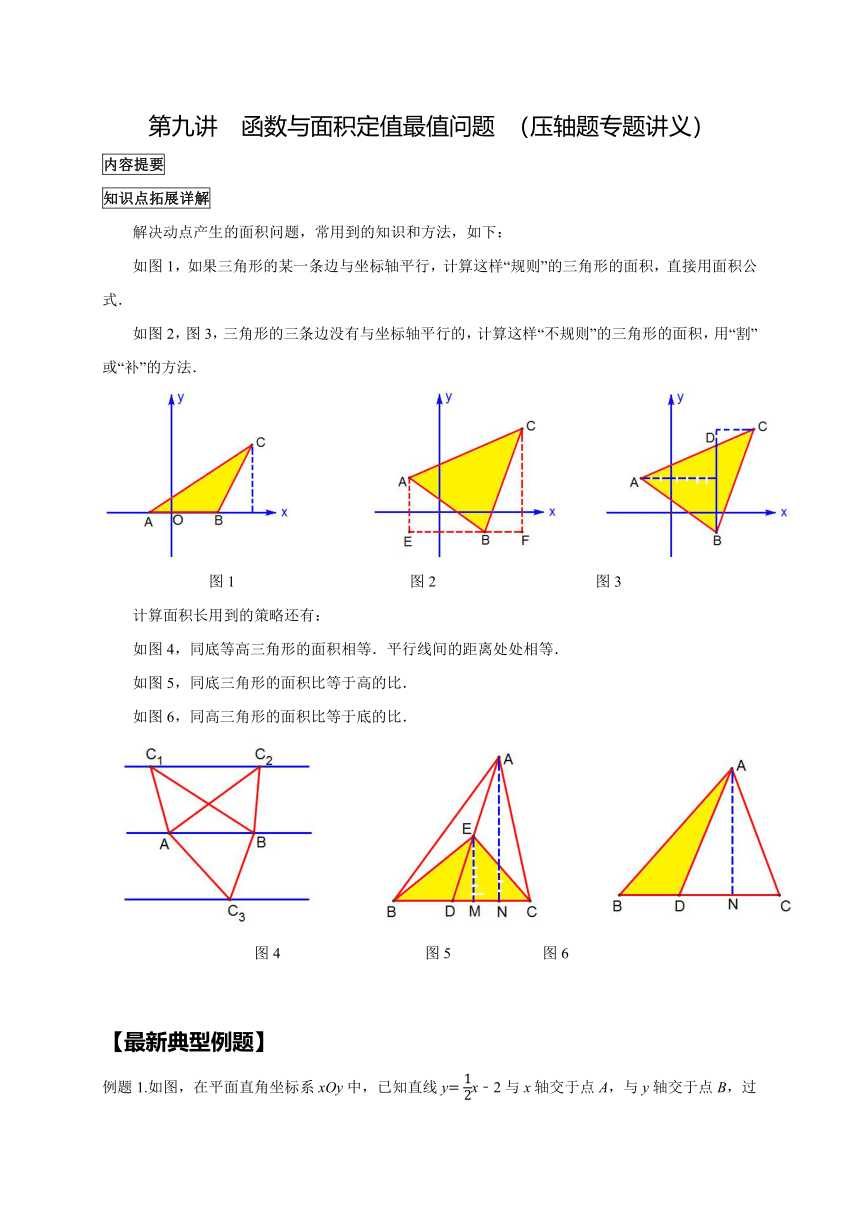 | |
| 格式 | docx | ||
| 文件大小 | 1019.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 15:16:19 | ||
图片预览




文档简介
第九讲 函数与面积定值最值问题 (压轴题专题讲义)
内容提要
知识点拓展详解
解决动点产生的面积问题,常用到的知识和方法,如下:
如图1,如果三角形的某一条边与坐标轴平行,计算这样“规则”的三角形的面积,直接用面积公式.
如图2,图3,三角形的三条边没有与坐标轴平行的,计算这样“不规则”的三角形的面积,用“割”或“补”的方法.
图1 图2 图3
计算面积长用到的策略还有:
如图4,同底等高三角形的面积相等.平行线间的距离处处相等.
如图5,同底三角形的面积比等于高的比.
如图6,同高三角形的面积比等于底的比.
图4 图5 图6
【最新典型例题】
例题1.如图,在平面直角坐标系xOy中,已知直线yx﹣2与x轴交于点A,与y轴交于点B,过A、B两点的抛物线y=ax2+bx+c与x轴交于另一点C(﹣1,0).
(1)求抛物线的解析式;
(2)在抛物线上是否存在一点P,使S△PAB=S△OAB?若存在,请求出点P的坐标,若不存在,请说明理由;
(3)点M为直线AB下方抛物线上一点,点N为y轴上一点,当△MAB的面积最大时,求MNON的最小值.
【分析】(1)先求出点A,点B坐标,利用待定系数法可求解析式;
(2)分两种情况讨论,利用平行线之间的距离相等,可求OP解析式,EP''的解析式,联立方程组可求解;
(3)过点M作MF⊥AC,交AB于F,设点M(m,m2m﹣2),则点F(m,m﹣2),可求MF的长,由三角形面积公式可求△MAB的面积=﹣(m﹣2)2+4,利用二次函数的性质可求点M坐标,过点O作∠KOB=30°,过点N作KN⊥OK于K点,过点M作MP⊥OK于P,延长MF交直线KO于Q,由直角三角形的性质可得KNON,可得MNON=MN+KN,则当点M,点N,点K三点共线,且垂直于OK时,MNON有最小值,即最小值为MP,由直角三角形的性质可求解.
【解析】(1)∵直线yx﹣2与x轴交于点A,与y轴交于点B,
∴点A(4,0),点B(0,﹣2),
设抛物线解析式为:y=a(x+1)(x﹣4),
∴﹣2=﹣4a,
∴a,
∴抛物线解析式为:y(x+1)(x﹣4)x2x﹣2;
(2)如图1,当点P在直线AB上方时,过点O作OP∥AB,交抛物线于点P,
∵OP∥AB,
∴△ABP和△ABO是等底等高的两个三角形,
∴S△PAB=S△ABO,
∵OP∥AB,
∴直线PO的解析式为yx,
联立方程组可得,
解得:或,
∴点P(2+2,1)或(2﹣2,1);
当点P''在直线AB下方时,在OB的延长线上截取BE=OB=2,过点E作EP''∥AB,交抛物线于点P'',连接AP'',BP'',
∴AB∥EP''∥OP,OB=BE,
∴S△AP''B=S△ABO,
∵EP''∥AB,且过点E(0,﹣4),
∴直线EP''解析式为yx﹣4,
联立方程组可得,
解得,
∴点P''(2,﹣3),
综上所述:点P坐标为(2+2,1)或(2﹣2,1)或(2,﹣3);
(3)如图2,过点M作MF⊥AC,交AB于F,
设点M(m,m2m﹣2),则点F(m,m﹣2),
∴MFm﹣2﹣(m2m﹣2)(m﹣2)2+2,
∴△MAB的面积4×[(m﹣2)2+2]=﹣(m﹣2)2+4,
∴当m=2时,△MAB的面积有最大值,
∴点M(2,﹣3),
如图3,过点O作∠KOB=30°,过点N作KN⊥OK于K点,过点M作MP⊥OK于P,延长MF交直线KO于Q,
∵∠KOB=30°,KN⊥OK,∴KNON,∴MNON=MN+KN,
∴当点M,点N,点K三点共线,且垂直于OK时,MNON有最小值,即最小值为MP,
∵∠KOB=30°,∴直线OK解析式为yx,当x=2时,点Q(2,2),
∴QM=23,∵OB∥QM,∴∠PQM=∠PON=30°,∴PMQM,
∴MNON的最小值为.
强化同步练习
一.选择题(共4小题)
1.如图,矩形OABC的长OA=,宽OC=1,将△AOC沿AC翻折得△APC,可得下列结论:①∠PCB=30°;②点P的坐标是();③若P、C两点在抛物线上,则b的值是,c的值是1;④在③中的抛物线CP段(不包括C、P两点)上,存在一点Q,使四边形QCAP的面积最大,最大值为.其中正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
2.如图,矩形ABCD中,E是AB的中点,将△ADE沿DE翻折,点A落在点F处,tan∠CDE=.设AB=x,△ABF的面积为y,则y与x的函数图象大致为( )
A. B.
C. D.
3.如图,小明设计了一个电子游戏,一个跳蚤从横坐标为t(t>0)的P1点开始按点的横坐标依次增加1的规律,在抛物线y=ax2上向右跳动,得到P1,P2,P3,这时△P1P2P3面积为( )
A.a B.2a C.3a D.4a
4.如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc<0;③a+b≥am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题)
5.如图,点A是抛物线y=2x2﹣3x+2上的动点.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为 .
6.如图在矩形ABCD中,AB=12cm,AD=4cm,点P,Q分别从A,B同时出发,P在AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度运动,当点Q到达点C时,两点同时停止运动,则当运动 秒时,△PBQ的面积最大值为 cm2.
7.如图,在平面直角坐标系中,点 A、点B均在抛物线y=x2上,且AB∥x轴,点 C、点D为线段AB的三等分点,以CD为边向下作矩形CDEF,矩形CDEF的顶点 E、F均在此抛物线上,若矩形CDEF的面积为2,则AB的长为 .
8.如图,抛物线y=x2﹣4的顶点为点P,直线y=1与抛物线相交于A,B两点,则△APB的面积是 .
9.如图,抛物线y=﹣x2+2x+c交x轴于点A(﹣1,0)、B,交y轴于点C,D为抛物线的顶点.
(1)点D坐标为 ;
(2)点C关于抛物线对称轴的对称点为E点,点M是抛物线对称轴上一点,且△DMB和△BCE相似,点M坐标为 .
10.已知点A(2,4),B(0,1),点M在抛物线y=x2上运动,则AM+BM的最小值为 .
11.已知二次函数y=x﹣2与x轴交于A、B两点,与y轴交于点C.
(1)如图1,点P为抛物线上B、C两点间一动点,连接BP,连接AP、BC交于点Q,则的最大值为 .
(2)如图2,将抛物线沿射线CB方向平移,点C平移至点C1处,且OC1=OC,动点M在平移后抛物线的对称轴上,当△C1BM为直角三角形时,点M的坐标为 .
三.解答题(共4小题)
12.如图1,在平面直角坐标系中,抛物线与x轴分别交于A,B两点,与y轴交于C点,其中B(4,0),C(0,2).
(1)求该抛物线的函数表达式;
(2)点P为直线BC上方抛物线上的任意一点,过P作PD∥AC交直线BC于D,作PE∥x轴交直线BC于E,求的最大值,并求此时P的坐标;
(3)如图2,在(2)中取得最大值的条件下,将该抛物线沿着水平方向右平移2个单位长度,点F为点P的对应点,M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点C,F,M,N为顶点的四边形是平行四边形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
13.如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)和B(﹣1,0)两点,与y轴交于点C,点P是直线AC下方的抛物线上一动点.
(1)求抛物线的解析式:
(2)过点P作PF⊥直线AC于点F,过点P作PD⊥x轴于点D,交直线AC于点E,求PF的最大值及此时点P的坐标;
(3)取(2)中PF最大值时的P点,在坐标平面内是否存在点Q,使得以点A、C、P、Q为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标,若不存在,请说明理由.
14.如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2).
(1)求二次函数的解析式;
(2)点P在该二次函数图象的对称轴上,且使|PB﹣PC|最大,求点P的坐标;
(3)若点M为该二次函数图象在第四象限内一个动点,当点M运动到何处时,四边形ACMB的面积最大?求出此时点M的坐标及四边形ACMB面积的最大值.
15.如图,抛物线y=﹣x2+4x+5与x轴交于点A和点B,与y轴交于点C.
(1)求出A、B、C三点的坐标;
(2)将抛物线y=﹣x2+4x+5图象x轴上方部分沿x轴向下翻折,保留抛物线与x轴的交点和x轴下方图象,得到的新图象记作M,图象M与直线y=t恒有四个交点,从左到右四个交点依次记为D,E,F,G.若以EF为直径作圆,该圆记作图象N.
①在图象M上找一点P,使得△PAB的面积为3,求出点P的坐标;
②当图象N与x轴相离时,直接写出t的取值范围.
参考答案与试题解析
一.选择题(共4小题)
1.如图,矩形OABC的长OA=,宽OC=1,将△AOC沿AC翻折得△APC,可得下列结论:①∠PCB=30°;②点P的坐标是();③若P、C两点在抛物线上,则b的值是,c的值是1;④在③中的抛物线CP段(不包括C、P两点)上,存在一点Q,使四边形QCAP的面积最大,最大值为.其中正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
【解答】解:在Rt△OAC中,OA=,OC=1,则∠OAC=30°,∠OCA=60°;
根据折叠的性质知:OA=AP=,∠ACO=∠ACP=60°;
①∵∠BCA=∠OAC=30°,且∠ACP=60°,
∴∠PCB=30°,故①正确;
②过P作PD⊥OA于D;
Rt△PAD中,∠PAD=60°,AP=;
∴OD=AD=,PD=,
所以P(,),故②正确;
③将P、C代入抛物线的解析式中,得:
,
解得;
故③错误;
④过Q作QM∥y轴,交CP于M;
由③知y=﹣x2+x+1,
由P(,),C(0,1)易求得直线PC:y=x+1;
设M(a,a+1),
则Q(a,﹣a2+a+1),则:
QM=﹣a2+a+1﹣(a+1)=﹣a2+a,
故S△QPC=QM |xP|=×(﹣a2+a)×=﹣a2+a,
由于S△APC=S△AOC=,
故四边形QCAP的面积S=S△QPC+S△APC=﹣a2+a+,
则Smax==;
故④正确;
所以正确的结论为①②④.
故选:B.
2.如图,矩形ABCD中,E是AB的中点,将△ADE沿DE翻折,点A落在点F处,tan∠CDE=.设AB=x,△ABF的面积为y,则y与x的函数图象大致为( )
A. B.
C. D.
【解答】解:设AB=x,AE=BE=x,
由折叠可知,EF=AE=BE=x,
则∠AFB=90°,
∵AB∥CD,
∴∠CDE=∠AED,
由tan∠CDE=得tan∠AED=,
设AD=x,AE=x,
∴DE=x
因为F、A关于DE对称,
∴AF⊥DE,
∴∠ADE=∠FAB,
∴△FAB∽△ADE,
∴,
∴,
该函数为经过原点的二次函数,
故选:C.
3.如图,小明设计了一个电子游戏,一个跳蚤从横坐标为t(t>0)的P1点开始按点的横坐标依次增加1的规律,在抛物线y=ax2上向右跳动,得到P1,P2,P3,这时△P1P2P3面积为( )
A.a B.2a C.3a D.4a
【解答】解:作P1A⊥x轴,P2B⊥x轴,P3C⊥x轴,垂足分别为A,B,C.
由题意得:A(t,0),B(t+1,0),C(t+2,0),
P1(t,at2),P2(t+1,at2+2at+a),P3(t+2,at2+4at+4a);
则:△P1P2P3的面积S=S梯形P1ACP3﹣S梯形P1ABP2﹣S梯形P2BCP3=(at2+at2+4at+4a)×2﹣(at2+at2+2at+a)﹣(at2+2at+a+at2+4at+4a)
=a.
故选:A.
4.如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc<0;③a+b≥am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),B(4,0),
∴对称轴为直线x==1,
∴﹣=1,
∴2a=﹣b,
∴2a+b=0,故①正确,符合题意;
∵抛物线开口向下,
∴a<0,
∴b=﹣2a>0,
∵抛物线交y轴的正半轴,
∴c>0,
∴abc<0,故②正确,符合题意;
∵抛物线的对称轴x=1,开口向下,
∴x=1时,y有最大值,最大值=a+b+c.
∴a+b+c≥am2+bm+c(m为任意实数),
∴a+b≥am2+bm(m为任意实数),故③正确,符合题意;
④∵C(0,c),
设直线BC的解析式为y=kx+t,
∴,
解得,
∴y=﹣x+c,
将点A(﹣2,0)代入y=ax2﹣2ax+c,
∴c=﹣8a.
∴y=ax2﹣2ax﹣8a.
过点Q作QN∥y轴交BC于点P,
∵Q(m,n),
∴P(m,2am﹣8a),
∴PQ=n﹣2am+8a.
∴S△QBC=×4×(n﹣2am+8a)=2(n﹣2am+8a),
∵n=am2﹣2am﹣8a,
∴S△QBC=2(am2﹣4am)=2a(m﹣2)2﹣8a.
∴当m=2时,△QBC的面积最大,
故④正确,符合题意;
故选:D.
二.填空题(共7小题)
5.如图,点A是抛物线y=2x2﹣3x+2上的动点.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为 .
【解答】解:∵四边形ABCD为矩形,
∴BD=AC,
∵y=2x2﹣3x+2=2(x﹣)2+,
∴抛物线顶点坐标为(,),
∴AC最小值为,
故答案为:.
6.如图在矩形ABCD中,AB=12cm,AD=4cm,点P,Q分别从A,B同时出发,P在AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度运动,当点Q到达点C时,两点同时停止运动,则当运动 3 秒时,△PBQ的面积最大值为 9 cm2.
【解答】解:设当运动x秒时,△PBQ的面积为ycm2,
可得y=x(12﹣2x),
整理得y=﹣(x﹣3)2+9(0<x≤4),
∵a=﹣1<0,
∴当x=3时,y取最大值9,
故答案为:3,9.
7.如图,在平面直角坐标系中,点 A、点B均在抛物线y=x2上,且AB∥x轴,点 C、点D为线段AB的三等分点,以CD为边向下作矩形CDEF,矩形CDEF的顶点 E、F均在此抛物线上,若矩形CDEF的面积为2,则AB的长为 3 .
【解答】解:抛物线y=x2的对称轴为y轴,
∵点 A、点B均在抛物线y=x2上,且AB∥x轴,
∴点 A、点B关于y轴对称,
设A(a,a2),则B(﹣a,a2),a>0.
∴AB=2a,点 A、点B到x轴的距离为a2.
∵点 C、点D为线段AB的三等分点,
∴CD=a.
设CD与y轴交于点H,
由题意,点 C、点D关于y轴对称,
∴HD=HC=a,
∵矩形CDEF的顶点 E、F均在此抛物线上,
∴E(﹣a,),F(a,),
∵EF∥x轴,
∴点 E、F到x轴的距离为2,
∵AB∥x轴,
∴DE=CF=,
∵矩形CDEF的面积为2,
∴CD CF=2,
∴a =2,
∴,
∴a=.
∴AB=2a=3.
故答案为:3.
8.如图,抛物线y=x2﹣4的顶点为点P,直线y=1与抛物线相交于A,B两点,则△APB的面积是 5 .
【解答】解:当y=1时,
1=x2﹣4,
解得:x=±,
∴A,B两点分别为(﹣,1),(,1),
∴AB=2,
根据题意P点为(0,﹣4),
∴△APB的高为1﹣(﹣4)=5,
∴△APB的面积是×2×5=5.
故答案为:5.
9.如图,抛物线y=﹣x2+2x+c交x轴于点A(﹣1,0)、B,交y轴于点C,D为抛物线的顶点.
(1)点D坐标为 (1,4) ;
(2)点C关于抛物线对称轴的对称点为E点,点M是抛物线对称轴上一点,且△DMB和△BCE相似,点M坐标为 (1,﹣2)或(1,) .
解:(1)∵抛物线y=﹣x2+2x+c交x轴于点A(﹣1,0),
∴﹣1﹣2+c=0.
∴c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
∵y=﹣(x﹣1)2+4,
∴D(1,4).
故答案为:(1,4);
(2)∵y=﹣(x﹣1)2+4,
∴抛物线的对称轴为直线x=1.
∴OF=1,DF=4.
令x=0,则y=3,
∴C(0,3).
∴E(2,3)
∴OC=3,CE=2.
令y=0,则﹣x2+2x+3=0.
解得:x=﹣1或3.
∴B(3,0).
∴OB=3.
∴OB=OC.
∴∠OCB=∠OBC=45°.
∵CE∥OB,
∴∠C=45°.
由于点M是抛物线对称轴上一点,且△DMB和△BCE相似,
此时有两种情况:在DF上取点M,M′,连接BM,BM′,如图,
当△DMB∽△BCE时,
∴∠M=∠C=45°.
∵FM⊥OB,
∴BF=FM.
∵BF=OB﹣OF=2,
∴FM=2.
∴M(1,﹣2).
当△DM′B∽△BEC时,
∴.
∵DB==2,BC==3,
∴.
∴BM′=.
∴M′F=.
∴M′(1,).
综上,点M坐标为(1,﹣2)或(1,).
故答案为:(1,﹣2)或(1,).
10.已知点A(2,4),B(0,1),点M在抛物线y=x2上运动,则AM+BM的最小值为 5 .
解:设点M(m,m2),
则点M到x轴距离为m2,BM==m2+1,
∴点M到点B的距离与点M到直线y=﹣1的距离相等,
∵点A横坐标为x=2,
∴点M为直线x=2与抛物线交点,
如图,设直线x=2与直线y=﹣1交点B'(2,﹣1),
∴AB'为AM+BM最小值,AB'=4﹣(﹣1)=5,
故答案为:5.
11.已知二次函数y=x﹣2与x轴交于A、B两点,与y轴交于点C.
(1)如图1,点P为抛物线上B、C两点间一动点,连接BP,连接AP、BC交于点Q,则的最大值为 .
(2)如图2,将抛物线沿射线CB方向平移,点C平移至点C1处,且OC1=OC,动点M在平移后抛物线的对称轴上,当△C1BM为直角三角形时,点M的坐标为 (,﹣)或(,)或(,)或(,) .
解:(1)令x=0,则y=﹣2,
∴C(0,﹣2),
令y=0,则x﹣2=0,
∴x=4或x=﹣1,
∴A(﹣1,0),B(4,0),
设BC的解析式为y=kx+b,
∴
∴,
∴y=x﹣2,
设P(t,t2﹣t﹣2),则F(t,t﹣2),E(﹣1,﹣),
∴PF=﹣t2+2t,AE=,
如图1,过点P作PF⊥x轴交BC于点F,过点A作AE⊥x轴交BC于点E,
∵PF∥AE,
∴=,
∵=,
∴=﹣(t﹣2)2+,
当t=2时,的最大值为,
故答案为:;
(2)由抛物线沿射线CB方向平移,设向右平移m个单位,则向上平移m个单位,
∴平移后C1(m,﹣2+m),
∵OC1=OC,
∴2=,
∴m=0(舍)或m=,
∴C1(,﹣),
∴平移后的抛物线解析式为y=(x﹣)2﹣,
∴对称轴为直线x=,
设M(,n),
①如图2,当∠BC1M=90°时,
过点C1作C1R⊥x轴交于R,过点M作MS⊥RC1交于S点,
∵∠RC1B+∠RBC1=90°,∠RC1B+∠SC1M=90°,
∴∠RBC1=∠SC1M,
∴△RBC1∽△SC1M,
∴=,
∵RB=,RC1=,SC1=﹣n﹣,SM=,
∴=,
∴n=﹣,
∴M(,﹣);
②如图3,当∠BMC1=90°,M点在x轴上方时,
过点M作MK∥x轴,过点B作BK⊥MK交于K,过点C1作C1L⊥MK交于L,
∵∠KMB+∠MBK=90°,∠KMB+∠LMC1=90°,
∴∠KBM=∠LMC1,
∴△MKB∽△C1LM,
∴=,
∵MK=,BK=n,LM=,LC1=n+,
∴=,
∴n=,
∴M(,);
③如图4,当∠BMC1=90°,M点在x轴下方时,
过点M作MU∥x轴,过点B作BV⊥MU交于V,过点C1作C1U⊥MU交于U,
∵∠VMB+∠MBV=90°,∠VMB+∠UMC1=90°,
∴∠VBM=∠UMC1,
∴△MVB∽△C1UM,
∴=,
∵MV=,BV=﹣n,UM=,UC1=﹣n﹣,
∴=,
∴n=,
∴M(,);
④如图5,当∠MBC1=90°时,
过点B作GH⊥x轴,过点M作MG⊥GH交于G,过点C1作C1H⊥GH交于H,
∵∠GMB+∠MBG=90°,∠GMB+∠HMC1=90°,
∴∠GBM=∠HMC1,
∴△MGB∽△C1HM,
∴=,
∵MG=,BG=n,BH=,HC1=,
∴=,
∴n=,
∴M(,);
综上所述:M点坐标为(,﹣)或(,)或(,)或(,),
故答案为:(,﹣)或(,)或(,)或(,).
三.解答题(共4小题)
12.如图1,在平面直角坐标系中,抛物线与x轴分别交于A,B两点,与y轴交于C点,其中B(4,0),C(0,2).
(1)求该抛物线的函数表达式;
(2)点P为直线BC上方抛物线上的任意一点,过P作PD∥AC交直线BC于D,作PE∥x轴交直线BC于E,求的最大值,并求此时P的坐标;
(3)如图2,在(2)中取得最大值的条件下,将该抛物线沿着水平方向右平移2个单位长度,点F为点P的对应点,M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点C,F,M,N为顶点的四边形是平行四边形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
解:(1)把B(4,0),C(0,2)代入y=﹣x2+bx+c得:
,
解得,
∴抛物线的函数表达式为y=﹣x2+x+2;
(2)如图,过点P作PQ∥y轴交BC于Q,过A作AH∥BC交y轴于H,
∵PE∥x轴,
∴PE⊥PQ,∠PEQ=∠OBC,
∴∠EPQ=∠BOC,
∴△PEQ∽△OBC,
∵PD∥AC,AH∥BC,
∴∠PQD=∠OCQ=∠CHA,∠PDE=∠ACD,∠ACD+∠CAH=∠PDE+∠PDQ=180°,
∴∠PDQ=∠CAH,
∴△PDQ∽△CAH,
∵y=﹣x2+x+2与x轴分别交于A,B两点,B(4,0),
∴A(﹣2,0),
∵C(0,2),
∴OC=2,OB=4,OA=2,AC=2,
∴,,
∴PE=2PQ,
∵∠OCQ=∠CHA,
∴tan∠OCQ=tan∠OHA,
∴,即,
∴OH=1,
∴CH=3,
∴,
∴,
∴,
∴当PQ取得最大值时,有最大值
设直线CB的解析式为y=kx+p,
则,解得:,
∴直线CB的解析式为,
设,则,
∴=﹣(t﹣2)2+1,
∵,开口向下
∴当t=2时,PQ取得最大值1,此时P(2,2),
∴的最大值为,此时P(2,2);
(3)由题意得:平移后抛物线解析式为,F(4,2),
∵抛物线的对称轴为直线x=3,
∴设,
分情况讨论:
①当CF为对角线时,则3+n=0+4,
解得:n=1,
∴;
②当CM为对角线时,n+4=0+3,
解得:n=﹣1,
∴
③当CN为对角线时,n+0=4+3,
解得:n=7,
∴,
综上所述,点N的坐标为:,,.
13.如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)和B(﹣1,0)两点,与y轴交于点C,点P是直线AC下方的抛物线上一动点.
(1)求抛物线的解析式:
(2)过点P作PF⊥直线AC于点F,过点P作PD⊥x轴于点D,交直线AC于点E,求PF的最大值及此时点P的坐标;
(3)取(2)中PF最大值时的P点,在坐标平面内是否存在点Q,使得以点A、C、P、Q为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标,若不存在,请说明理由.
解:(1)将A(4,0)、B(﹣1,0)代入y=ax2+bx﹣4,
∴,
解得,
∴y=x2﹣3x﹣4;
(2)∵y=x2﹣3x﹣4与y轴交于点C,
∴点C的坐标为(0,﹣4),
设直线AC的解析式为y=kx﹣4,
∵直线AC经过点A(4,0),
∴0=4k﹣4,
解得:k=1,
∴直线AC的解析式为y=x﹣4,
设点P(x,x2﹣3x﹣4),则E(x,x﹣4),
∴PE=x﹣4﹣x2+3x+4=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,PE最大,最大值是4.
∵A(4,0),C(0,﹣4),
∴OA=OC,
∴∠OCA=45°,
∵PD⊥x轴,
∴∠CEP=∠OCA=45°,
∵PF⊥AC,
∴△PFE是等腰直角三角形,
∴PF=PE,
∴PE+PF=PE+PE=PE,
∴PE+PF的最大值为4,此时点P的坐标为(2,﹣6);
(3)①当CP为对角线时,由中点坐标公式得(2+0)=(m+4)且(﹣4﹣6)=(n+0),
解得,
∴点Q的坐标为(﹣2,﹣10);
②当AC为对角线时,
同理可得:(2+m)=(0+4)且(n﹣6)=(﹣4+0),
解得,
∴点Q的坐标为(2,2);
③当AP是对角线时,
同理可得:(0+m)=(2+4)且(0﹣6)=(n﹣4),
解得,
∴点Q的坐标为(6,﹣2);
故存在,点Q的坐标为(﹣2,﹣10)或(2,2)或(6,﹣2).
14.如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2).
(1)求二次函数的解析式;
(2)点P在该二次函数图象的对称轴上,且使|PB﹣PC|最大,求点P的坐标;
(3)若点M为该二次函数图象在第四象限内一个动点,当点M运动到何处时,四边形ACMB的面积最大?求出此时点M的坐标及四边形ACMB面积的最大值.
解:(1)将A(﹣1,0),B(2,0),C(0,﹣2)代入y=ax2+bx+c,
∴,
解得,
∴y=x2﹣x﹣2;
(2)∵y=x2﹣x﹣2=(x﹣)2﹣,
∴抛物线的对称轴为直线x=,
作C点关于对称轴的对称点C',连接BC'与对称轴交于点P,
∵CP=C'P,
∴|PB﹣PC|=|PB﹣PC'|≤BC',此时|PB﹣PC|有最大值,
∵C(0,﹣2),
∴C'(1,﹣2),
设直线BC'的解析式为y=kx+m,
∴,
解得,
∴y=2x﹣4,
∴P(,﹣3);
(3)过点M作MN∥y轴交BC于点N,
∵B(2,0),C(0,﹣2),
∴直线BC的解析式为y=x﹣2,
设M(t,t2﹣t﹣2),则N(t,t﹣2),
∴MN=t﹣2﹣(t2﹣t﹣2)=﹣t2+2t,
∴S△BCM=2×(﹣t2+2t)=﹣t2+2t,
∵S△ABC=3×2=3,
∴S四边形ACMB=3﹣t2+2t=﹣(t﹣1)2+4,
当t=1时,四边形ACMB的面积最大值为4,
此时M(1,﹣2).
15.如图,抛物线y=﹣x2+4x+5与x轴交于点A和点B,与y轴交于点C.
(1)求出A、B、C三点的坐标;
(2)将抛物线y=﹣x2+4x+5图象x轴上方部分沿x轴向下翻折,保留抛物线与x轴的交点和x轴下方图象,得到的新图象记作M,图象M与直线y=t恒有四个交点,从左到右四个交点依次记为D,E,F,G.若以EF为直径作圆,该圆记作图象N.
①在图象M上找一点P,使得△PAB的面积为3,求出点P的坐标;
②当图象N与x轴相离时,直接写出t的取值范围.
解:(1)令x=0,则y=5,
∴C(0,5),
令y=0,则﹣x2+4x+5=0,
解得x=5或x=﹣1,
∴A(﹣1,0),B(5,0);
(2)①设P点的纵坐标为m,
∵△PAB的面积为3,
∴6(﹣m)=3,
解得m=﹣1,
当﹣x2+4x+5=﹣1时,解得x=2+或x=2﹣,
∴P(2+,﹣1)或(2﹣,﹣1);
当﹣x2+4x+5=1时,解得x=2+或x=2﹣,
∴P(2+,﹣1)或(2﹣,﹣1);
综上所述:P点坐标为(2+,﹣1)或(2﹣,﹣1)或(2+,﹣1)或(2﹣,﹣1);
②∵y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴抛物线的顶点为(2,9),
∵图象M与直线y=t恒有四个交点,
∴﹣9<t≤0,
当﹣x2+4x+5=﹣t时,解得x=2+或x=2﹣,
∴E(2﹣,t),F(2+,t),
∴EF=2,
当=﹣t时,解得t=,
∵t<0,
∴t=,此时图象N与x轴相切,
∴﹣9<t<时,图象N与x轴相离.
内容提要
知识点拓展详解
解决动点产生的面积问题,常用到的知识和方法,如下:
如图1,如果三角形的某一条边与坐标轴平行,计算这样“规则”的三角形的面积,直接用面积公式.
如图2,图3,三角形的三条边没有与坐标轴平行的,计算这样“不规则”的三角形的面积,用“割”或“补”的方法.
图1 图2 图3
计算面积长用到的策略还有:
如图4,同底等高三角形的面积相等.平行线间的距离处处相等.
如图5,同底三角形的面积比等于高的比.
如图6,同高三角形的面积比等于底的比.
图4 图5 图6
【最新典型例题】
例题1.如图,在平面直角坐标系xOy中,已知直线yx﹣2与x轴交于点A,与y轴交于点B,过A、B两点的抛物线y=ax2+bx+c与x轴交于另一点C(﹣1,0).
(1)求抛物线的解析式;
(2)在抛物线上是否存在一点P,使S△PAB=S△OAB?若存在,请求出点P的坐标,若不存在,请说明理由;
(3)点M为直线AB下方抛物线上一点,点N为y轴上一点,当△MAB的面积最大时,求MNON的最小值.
【分析】(1)先求出点A,点B坐标,利用待定系数法可求解析式;
(2)分两种情况讨论,利用平行线之间的距离相等,可求OP解析式,EP''的解析式,联立方程组可求解;
(3)过点M作MF⊥AC,交AB于F,设点M(m,m2m﹣2),则点F(m,m﹣2),可求MF的长,由三角形面积公式可求△MAB的面积=﹣(m﹣2)2+4,利用二次函数的性质可求点M坐标,过点O作∠KOB=30°,过点N作KN⊥OK于K点,过点M作MP⊥OK于P,延长MF交直线KO于Q,由直角三角形的性质可得KNON,可得MNON=MN+KN,则当点M,点N,点K三点共线,且垂直于OK时,MNON有最小值,即最小值为MP,由直角三角形的性质可求解.
【解析】(1)∵直线yx﹣2与x轴交于点A,与y轴交于点B,
∴点A(4,0),点B(0,﹣2),
设抛物线解析式为:y=a(x+1)(x﹣4),
∴﹣2=﹣4a,
∴a,
∴抛物线解析式为:y(x+1)(x﹣4)x2x﹣2;
(2)如图1,当点P在直线AB上方时,过点O作OP∥AB,交抛物线于点P,
∵OP∥AB,
∴△ABP和△ABO是等底等高的两个三角形,
∴S△PAB=S△ABO,
∵OP∥AB,
∴直线PO的解析式为yx,
联立方程组可得,
解得:或,
∴点P(2+2,1)或(2﹣2,1);
当点P''在直线AB下方时,在OB的延长线上截取BE=OB=2,过点E作EP''∥AB,交抛物线于点P'',连接AP'',BP'',
∴AB∥EP''∥OP,OB=BE,
∴S△AP''B=S△ABO,
∵EP''∥AB,且过点E(0,﹣4),
∴直线EP''解析式为yx﹣4,
联立方程组可得,
解得,
∴点P''(2,﹣3),
综上所述:点P坐标为(2+2,1)或(2﹣2,1)或(2,﹣3);
(3)如图2,过点M作MF⊥AC,交AB于F,
设点M(m,m2m﹣2),则点F(m,m﹣2),
∴MFm﹣2﹣(m2m﹣2)(m﹣2)2+2,
∴△MAB的面积4×[(m﹣2)2+2]=﹣(m﹣2)2+4,
∴当m=2时,△MAB的面积有最大值,
∴点M(2,﹣3),
如图3,过点O作∠KOB=30°,过点N作KN⊥OK于K点,过点M作MP⊥OK于P,延长MF交直线KO于Q,
∵∠KOB=30°,KN⊥OK,∴KNON,∴MNON=MN+KN,
∴当点M,点N,点K三点共线,且垂直于OK时,MNON有最小值,即最小值为MP,
∵∠KOB=30°,∴直线OK解析式为yx,当x=2时,点Q(2,2),
∴QM=23,∵OB∥QM,∴∠PQM=∠PON=30°,∴PMQM,
∴MNON的最小值为.
强化同步练习
一.选择题(共4小题)
1.如图,矩形OABC的长OA=,宽OC=1,将△AOC沿AC翻折得△APC,可得下列结论:①∠PCB=30°;②点P的坐标是();③若P、C两点在抛物线上,则b的值是,c的值是1;④在③中的抛物线CP段(不包括C、P两点)上,存在一点Q,使四边形QCAP的面积最大,最大值为.其中正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
2.如图,矩形ABCD中,E是AB的中点,将△ADE沿DE翻折,点A落在点F处,tan∠CDE=.设AB=x,△ABF的面积为y,则y与x的函数图象大致为( )
A. B.
C. D.
3.如图,小明设计了一个电子游戏,一个跳蚤从横坐标为t(t>0)的P1点开始按点的横坐标依次增加1的规律,在抛物线y=ax2上向右跳动,得到P1,P2,P3,这时△P1P2P3面积为( )
A.a B.2a C.3a D.4a
4.如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc<0;③a+b≥am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题)
5.如图,点A是抛物线y=2x2﹣3x+2上的动点.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为 .
6.如图在矩形ABCD中,AB=12cm,AD=4cm,点P,Q分别从A,B同时出发,P在AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度运动,当点Q到达点C时,两点同时停止运动,则当运动 秒时,△PBQ的面积最大值为 cm2.
7.如图,在平面直角坐标系中,点 A、点B均在抛物线y=x2上,且AB∥x轴,点 C、点D为线段AB的三等分点,以CD为边向下作矩形CDEF,矩形CDEF的顶点 E、F均在此抛物线上,若矩形CDEF的面积为2,则AB的长为 .
8.如图,抛物线y=x2﹣4的顶点为点P,直线y=1与抛物线相交于A,B两点,则△APB的面积是 .
9.如图,抛物线y=﹣x2+2x+c交x轴于点A(﹣1,0)、B,交y轴于点C,D为抛物线的顶点.
(1)点D坐标为 ;
(2)点C关于抛物线对称轴的对称点为E点,点M是抛物线对称轴上一点,且△DMB和△BCE相似,点M坐标为 .
10.已知点A(2,4),B(0,1),点M在抛物线y=x2上运动,则AM+BM的最小值为 .
11.已知二次函数y=x﹣2与x轴交于A、B两点,与y轴交于点C.
(1)如图1,点P为抛物线上B、C两点间一动点,连接BP,连接AP、BC交于点Q,则的最大值为 .
(2)如图2,将抛物线沿射线CB方向平移,点C平移至点C1处,且OC1=OC,动点M在平移后抛物线的对称轴上,当△C1BM为直角三角形时,点M的坐标为 .
三.解答题(共4小题)
12.如图1,在平面直角坐标系中,抛物线与x轴分别交于A,B两点,与y轴交于C点,其中B(4,0),C(0,2).
(1)求该抛物线的函数表达式;
(2)点P为直线BC上方抛物线上的任意一点,过P作PD∥AC交直线BC于D,作PE∥x轴交直线BC于E,求的最大值,并求此时P的坐标;
(3)如图2,在(2)中取得最大值的条件下,将该抛物线沿着水平方向右平移2个单位长度,点F为点P的对应点,M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点C,F,M,N为顶点的四边形是平行四边形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
13.如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)和B(﹣1,0)两点,与y轴交于点C,点P是直线AC下方的抛物线上一动点.
(1)求抛物线的解析式:
(2)过点P作PF⊥直线AC于点F,过点P作PD⊥x轴于点D,交直线AC于点E,求PF的最大值及此时点P的坐标;
(3)取(2)中PF最大值时的P点,在坐标平面内是否存在点Q,使得以点A、C、P、Q为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标,若不存在,请说明理由.
14.如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2).
(1)求二次函数的解析式;
(2)点P在该二次函数图象的对称轴上,且使|PB﹣PC|最大,求点P的坐标;
(3)若点M为该二次函数图象在第四象限内一个动点,当点M运动到何处时,四边形ACMB的面积最大?求出此时点M的坐标及四边形ACMB面积的最大值.
15.如图,抛物线y=﹣x2+4x+5与x轴交于点A和点B,与y轴交于点C.
(1)求出A、B、C三点的坐标;
(2)将抛物线y=﹣x2+4x+5图象x轴上方部分沿x轴向下翻折,保留抛物线与x轴的交点和x轴下方图象,得到的新图象记作M,图象M与直线y=t恒有四个交点,从左到右四个交点依次记为D,E,F,G.若以EF为直径作圆,该圆记作图象N.
①在图象M上找一点P,使得△PAB的面积为3,求出点P的坐标;
②当图象N与x轴相离时,直接写出t的取值范围.
参考答案与试题解析
一.选择题(共4小题)
1.如图,矩形OABC的长OA=,宽OC=1,将△AOC沿AC翻折得△APC,可得下列结论:①∠PCB=30°;②点P的坐标是();③若P、C两点在抛物线上,则b的值是,c的值是1;④在③中的抛物线CP段(不包括C、P两点)上,存在一点Q,使四边形QCAP的面积最大,最大值为.其中正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
【解答】解:在Rt△OAC中,OA=,OC=1,则∠OAC=30°,∠OCA=60°;
根据折叠的性质知:OA=AP=,∠ACO=∠ACP=60°;
①∵∠BCA=∠OAC=30°,且∠ACP=60°,
∴∠PCB=30°,故①正确;
②过P作PD⊥OA于D;
Rt△PAD中,∠PAD=60°,AP=;
∴OD=AD=,PD=,
所以P(,),故②正确;
③将P、C代入抛物线的解析式中,得:
,
解得;
故③错误;
④过Q作QM∥y轴,交CP于M;
由③知y=﹣x2+x+1,
由P(,),C(0,1)易求得直线PC:y=x+1;
设M(a,a+1),
则Q(a,﹣a2+a+1),则:
QM=﹣a2+a+1﹣(a+1)=﹣a2+a,
故S△QPC=QM |xP|=×(﹣a2+a)×=﹣a2+a,
由于S△APC=S△AOC=,
故四边形QCAP的面积S=S△QPC+S△APC=﹣a2+a+,
则Smax==;
故④正确;
所以正确的结论为①②④.
故选:B.
2.如图,矩形ABCD中,E是AB的中点,将△ADE沿DE翻折,点A落在点F处,tan∠CDE=.设AB=x,△ABF的面积为y,则y与x的函数图象大致为( )
A. B.
C. D.
【解答】解:设AB=x,AE=BE=x,
由折叠可知,EF=AE=BE=x,
则∠AFB=90°,
∵AB∥CD,
∴∠CDE=∠AED,
由tan∠CDE=得tan∠AED=,
设AD=x,AE=x,
∴DE=x
因为F、A关于DE对称,
∴AF⊥DE,
∴∠ADE=∠FAB,
∴△FAB∽△ADE,
∴,
∴,
该函数为经过原点的二次函数,
故选:C.
3.如图,小明设计了一个电子游戏,一个跳蚤从横坐标为t(t>0)的P1点开始按点的横坐标依次增加1的规律,在抛物线y=ax2上向右跳动,得到P1,P2,P3,这时△P1P2P3面积为( )
A.a B.2a C.3a D.4a
【解答】解:作P1A⊥x轴,P2B⊥x轴,P3C⊥x轴,垂足分别为A,B,C.
由题意得:A(t,0),B(t+1,0),C(t+2,0),
P1(t,at2),P2(t+1,at2+2at+a),P3(t+2,at2+4at+4a);
则:△P1P2P3的面积S=S梯形P1ACP3﹣S梯形P1ABP2﹣S梯形P2BCP3=(at2+at2+4at+4a)×2﹣(at2+at2+2at+a)﹣(at2+2at+a+at2+4at+4a)
=a.
故选:A.
4.如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0),B(4,0),交y轴的正半轴于点C,对称轴交抛物线于点D,交x轴于点E,则下列结论:①2a+b=0;②abc<0;③a+b≥am2+bm(m为任意实数);④若点Q(m,n)是抛物线上第一象限上的动点,当△QBC的面积最大时,m=2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),B(4,0),
∴对称轴为直线x==1,
∴﹣=1,
∴2a=﹣b,
∴2a+b=0,故①正确,符合题意;
∵抛物线开口向下,
∴a<0,
∴b=﹣2a>0,
∵抛物线交y轴的正半轴,
∴c>0,
∴abc<0,故②正确,符合题意;
∵抛物线的对称轴x=1,开口向下,
∴x=1时,y有最大值,最大值=a+b+c.
∴a+b+c≥am2+bm+c(m为任意实数),
∴a+b≥am2+bm(m为任意实数),故③正确,符合题意;
④∵C(0,c),
设直线BC的解析式为y=kx+t,
∴,
解得,
∴y=﹣x+c,
将点A(﹣2,0)代入y=ax2﹣2ax+c,
∴c=﹣8a.
∴y=ax2﹣2ax﹣8a.
过点Q作QN∥y轴交BC于点P,
∵Q(m,n),
∴P(m,2am﹣8a),
∴PQ=n﹣2am+8a.
∴S△QBC=×4×(n﹣2am+8a)=2(n﹣2am+8a),
∵n=am2﹣2am﹣8a,
∴S△QBC=2(am2﹣4am)=2a(m﹣2)2﹣8a.
∴当m=2时,△QBC的面积最大,
故④正确,符合题意;
故选:D.
二.填空题(共7小题)
5.如图,点A是抛物线y=2x2﹣3x+2上的动点.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为 .
【解答】解:∵四边形ABCD为矩形,
∴BD=AC,
∵y=2x2﹣3x+2=2(x﹣)2+,
∴抛物线顶点坐标为(,),
∴AC最小值为,
故答案为:.
6.如图在矩形ABCD中,AB=12cm,AD=4cm,点P,Q分别从A,B同时出发,P在AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度运动,当点Q到达点C时,两点同时停止运动,则当运动 3 秒时,△PBQ的面积最大值为 9 cm2.
【解答】解:设当运动x秒时,△PBQ的面积为ycm2,
可得y=x(12﹣2x),
整理得y=﹣(x﹣3)2+9(0<x≤4),
∵a=﹣1<0,
∴当x=3时,y取最大值9,
故答案为:3,9.
7.如图,在平面直角坐标系中,点 A、点B均在抛物线y=x2上,且AB∥x轴,点 C、点D为线段AB的三等分点,以CD为边向下作矩形CDEF,矩形CDEF的顶点 E、F均在此抛物线上,若矩形CDEF的面积为2,则AB的长为 3 .
【解答】解:抛物线y=x2的对称轴为y轴,
∵点 A、点B均在抛物线y=x2上,且AB∥x轴,
∴点 A、点B关于y轴对称,
设A(a,a2),则B(﹣a,a2),a>0.
∴AB=2a,点 A、点B到x轴的距离为a2.
∵点 C、点D为线段AB的三等分点,
∴CD=a.
设CD与y轴交于点H,
由题意,点 C、点D关于y轴对称,
∴HD=HC=a,
∵矩形CDEF的顶点 E、F均在此抛物线上,
∴E(﹣a,),F(a,),
∵EF∥x轴,
∴点 E、F到x轴的距离为2,
∵AB∥x轴,
∴DE=CF=,
∵矩形CDEF的面积为2,
∴CD CF=2,
∴a =2,
∴,
∴a=.
∴AB=2a=3.
故答案为:3.
8.如图,抛物线y=x2﹣4的顶点为点P,直线y=1与抛物线相交于A,B两点,则△APB的面积是 5 .
【解答】解:当y=1时,
1=x2﹣4,
解得:x=±,
∴A,B两点分别为(﹣,1),(,1),
∴AB=2,
根据题意P点为(0,﹣4),
∴△APB的高为1﹣(﹣4)=5,
∴△APB的面积是×2×5=5.
故答案为:5.
9.如图,抛物线y=﹣x2+2x+c交x轴于点A(﹣1,0)、B,交y轴于点C,D为抛物线的顶点.
(1)点D坐标为 (1,4) ;
(2)点C关于抛物线对称轴的对称点为E点,点M是抛物线对称轴上一点,且△DMB和△BCE相似,点M坐标为 (1,﹣2)或(1,) .
解:(1)∵抛物线y=﹣x2+2x+c交x轴于点A(﹣1,0),
∴﹣1﹣2+c=0.
∴c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
∵y=﹣(x﹣1)2+4,
∴D(1,4).
故答案为:(1,4);
(2)∵y=﹣(x﹣1)2+4,
∴抛物线的对称轴为直线x=1.
∴OF=1,DF=4.
令x=0,则y=3,
∴C(0,3).
∴E(2,3)
∴OC=3,CE=2.
令y=0,则﹣x2+2x+3=0.
解得:x=﹣1或3.
∴B(3,0).
∴OB=3.
∴OB=OC.
∴∠OCB=∠OBC=45°.
∵CE∥OB,
∴∠C=45°.
由于点M是抛物线对称轴上一点,且△DMB和△BCE相似,
此时有两种情况:在DF上取点M,M′,连接BM,BM′,如图,
当△DMB∽△BCE时,
∴∠M=∠C=45°.
∵FM⊥OB,
∴BF=FM.
∵BF=OB﹣OF=2,
∴FM=2.
∴M(1,﹣2).
当△DM′B∽△BEC时,
∴.
∵DB==2,BC==3,
∴.
∴BM′=.
∴M′F=.
∴M′(1,).
综上,点M坐标为(1,﹣2)或(1,).
故答案为:(1,﹣2)或(1,).
10.已知点A(2,4),B(0,1),点M在抛物线y=x2上运动,则AM+BM的最小值为 5 .
解:设点M(m,m2),
则点M到x轴距离为m2,BM==m2+1,
∴点M到点B的距离与点M到直线y=﹣1的距离相等,
∵点A横坐标为x=2,
∴点M为直线x=2与抛物线交点,
如图,设直线x=2与直线y=﹣1交点B'(2,﹣1),
∴AB'为AM+BM最小值,AB'=4﹣(﹣1)=5,
故答案为:5.
11.已知二次函数y=x﹣2与x轴交于A、B两点,与y轴交于点C.
(1)如图1,点P为抛物线上B、C两点间一动点,连接BP,连接AP、BC交于点Q,则的最大值为 .
(2)如图2,将抛物线沿射线CB方向平移,点C平移至点C1处,且OC1=OC,动点M在平移后抛物线的对称轴上,当△C1BM为直角三角形时,点M的坐标为 (,﹣)或(,)或(,)或(,) .
解:(1)令x=0,则y=﹣2,
∴C(0,﹣2),
令y=0,则x﹣2=0,
∴x=4或x=﹣1,
∴A(﹣1,0),B(4,0),
设BC的解析式为y=kx+b,
∴
∴,
∴y=x﹣2,
设P(t,t2﹣t﹣2),则F(t,t﹣2),E(﹣1,﹣),
∴PF=﹣t2+2t,AE=,
如图1,过点P作PF⊥x轴交BC于点F,过点A作AE⊥x轴交BC于点E,
∵PF∥AE,
∴=,
∵=,
∴=﹣(t﹣2)2+,
当t=2时,的最大值为,
故答案为:;
(2)由抛物线沿射线CB方向平移,设向右平移m个单位,则向上平移m个单位,
∴平移后C1(m,﹣2+m),
∵OC1=OC,
∴2=,
∴m=0(舍)或m=,
∴C1(,﹣),
∴平移后的抛物线解析式为y=(x﹣)2﹣,
∴对称轴为直线x=,
设M(,n),
①如图2,当∠BC1M=90°时,
过点C1作C1R⊥x轴交于R,过点M作MS⊥RC1交于S点,
∵∠RC1B+∠RBC1=90°,∠RC1B+∠SC1M=90°,
∴∠RBC1=∠SC1M,
∴△RBC1∽△SC1M,
∴=,
∵RB=,RC1=,SC1=﹣n﹣,SM=,
∴=,
∴n=﹣,
∴M(,﹣);
②如图3,当∠BMC1=90°,M点在x轴上方时,
过点M作MK∥x轴,过点B作BK⊥MK交于K,过点C1作C1L⊥MK交于L,
∵∠KMB+∠MBK=90°,∠KMB+∠LMC1=90°,
∴∠KBM=∠LMC1,
∴△MKB∽△C1LM,
∴=,
∵MK=,BK=n,LM=,LC1=n+,
∴=,
∴n=,
∴M(,);
③如图4,当∠BMC1=90°,M点在x轴下方时,
过点M作MU∥x轴,过点B作BV⊥MU交于V,过点C1作C1U⊥MU交于U,
∵∠VMB+∠MBV=90°,∠VMB+∠UMC1=90°,
∴∠VBM=∠UMC1,
∴△MVB∽△C1UM,
∴=,
∵MV=,BV=﹣n,UM=,UC1=﹣n﹣,
∴=,
∴n=,
∴M(,);
④如图5,当∠MBC1=90°时,
过点B作GH⊥x轴,过点M作MG⊥GH交于G,过点C1作C1H⊥GH交于H,
∵∠GMB+∠MBG=90°,∠GMB+∠HMC1=90°,
∴∠GBM=∠HMC1,
∴△MGB∽△C1HM,
∴=,
∵MG=,BG=n,BH=,HC1=,
∴=,
∴n=,
∴M(,);
综上所述:M点坐标为(,﹣)或(,)或(,)或(,),
故答案为:(,﹣)或(,)或(,)或(,).
三.解答题(共4小题)
12.如图1,在平面直角坐标系中,抛物线与x轴分别交于A,B两点,与y轴交于C点,其中B(4,0),C(0,2).
(1)求该抛物线的函数表达式;
(2)点P为直线BC上方抛物线上的任意一点,过P作PD∥AC交直线BC于D,作PE∥x轴交直线BC于E,求的最大值,并求此时P的坐标;
(3)如图2,在(2)中取得最大值的条件下,将该抛物线沿着水平方向右平移2个单位长度,点F为点P的对应点,M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点C,F,M,N为顶点的四边形是平行四边形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
解:(1)把B(4,0),C(0,2)代入y=﹣x2+bx+c得:
,
解得,
∴抛物线的函数表达式为y=﹣x2+x+2;
(2)如图,过点P作PQ∥y轴交BC于Q,过A作AH∥BC交y轴于H,
∵PE∥x轴,
∴PE⊥PQ,∠PEQ=∠OBC,
∴∠EPQ=∠BOC,
∴△PEQ∽△OBC,
∵PD∥AC,AH∥BC,
∴∠PQD=∠OCQ=∠CHA,∠PDE=∠ACD,∠ACD+∠CAH=∠PDE+∠PDQ=180°,
∴∠PDQ=∠CAH,
∴△PDQ∽△CAH,
∵y=﹣x2+x+2与x轴分别交于A,B两点,B(4,0),
∴A(﹣2,0),
∵C(0,2),
∴OC=2,OB=4,OA=2,AC=2,
∴,,
∴PE=2PQ,
∵∠OCQ=∠CHA,
∴tan∠OCQ=tan∠OHA,
∴,即,
∴OH=1,
∴CH=3,
∴,
∴,
∴,
∴当PQ取得最大值时,有最大值
设直线CB的解析式为y=kx+p,
则,解得:,
∴直线CB的解析式为,
设,则,
∴=﹣(t﹣2)2+1,
∵,开口向下
∴当t=2时,PQ取得最大值1,此时P(2,2),
∴的最大值为,此时P(2,2);
(3)由题意得:平移后抛物线解析式为,F(4,2),
∵抛物线的对称轴为直线x=3,
∴设,
分情况讨论:
①当CF为对角线时,则3+n=0+4,
解得:n=1,
∴;
②当CM为对角线时,n+4=0+3,
解得:n=﹣1,
∴
③当CN为对角线时,n+0=4+3,
解得:n=7,
∴,
综上所述,点N的坐标为:,,.
13.如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)和B(﹣1,0)两点,与y轴交于点C,点P是直线AC下方的抛物线上一动点.
(1)求抛物线的解析式:
(2)过点P作PF⊥直线AC于点F,过点P作PD⊥x轴于点D,交直线AC于点E,求PF的最大值及此时点P的坐标;
(3)取(2)中PF最大值时的P点,在坐标平面内是否存在点Q,使得以点A、C、P、Q为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标,若不存在,请说明理由.
解:(1)将A(4,0)、B(﹣1,0)代入y=ax2+bx﹣4,
∴,
解得,
∴y=x2﹣3x﹣4;
(2)∵y=x2﹣3x﹣4与y轴交于点C,
∴点C的坐标为(0,﹣4),
设直线AC的解析式为y=kx﹣4,
∵直线AC经过点A(4,0),
∴0=4k﹣4,
解得:k=1,
∴直线AC的解析式为y=x﹣4,
设点P(x,x2﹣3x﹣4),则E(x,x﹣4),
∴PE=x﹣4﹣x2+3x+4=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,PE最大,最大值是4.
∵A(4,0),C(0,﹣4),
∴OA=OC,
∴∠OCA=45°,
∵PD⊥x轴,
∴∠CEP=∠OCA=45°,
∵PF⊥AC,
∴△PFE是等腰直角三角形,
∴PF=PE,
∴PE+PF=PE+PE=PE,
∴PE+PF的最大值为4,此时点P的坐标为(2,﹣6);
(3)①当CP为对角线时,由中点坐标公式得(2+0)=(m+4)且(﹣4﹣6)=(n+0),
解得,
∴点Q的坐标为(﹣2,﹣10);
②当AC为对角线时,
同理可得:(2+m)=(0+4)且(n﹣6)=(﹣4+0),
解得,
∴点Q的坐标为(2,2);
③当AP是对角线时,
同理可得:(0+m)=(2+4)且(0﹣6)=(n﹣4),
解得,
∴点Q的坐标为(6,﹣2);
故存在,点Q的坐标为(﹣2,﹣10)或(2,2)或(6,﹣2).
14.如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2).
(1)求二次函数的解析式;
(2)点P在该二次函数图象的对称轴上,且使|PB﹣PC|最大,求点P的坐标;
(3)若点M为该二次函数图象在第四象限内一个动点,当点M运动到何处时,四边形ACMB的面积最大?求出此时点M的坐标及四边形ACMB面积的最大值.
解:(1)将A(﹣1,0),B(2,0),C(0,﹣2)代入y=ax2+bx+c,
∴,
解得,
∴y=x2﹣x﹣2;
(2)∵y=x2﹣x﹣2=(x﹣)2﹣,
∴抛物线的对称轴为直线x=,
作C点关于对称轴的对称点C',连接BC'与对称轴交于点P,
∵CP=C'P,
∴|PB﹣PC|=|PB﹣PC'|≤BC',此时|PB﹣PC|有最大值,
∵C(0,﹣2),
∴C'(1,﹣2),
设直线BC'的解析式为y=kx+m,
∴,
解得,
∴y=2x﹣4,
∴P(,﹣3);
(3)过点M作MN∥y轴交BC于点N,
∵B(2,0),C(0,﹣2),
∴直线BC的解析式为y=x﹣2,
设M(t,t2﹣t﹣2),则N(t,t﹣2),
∴MN=t﹣2﹣(t2﹣t﹣2)=﹣t2+2t,
∴S△BCM=2×(﹣t2+2t)=﹣t2+2t,
∵S△ABC=3×2=3,
∴S四边形ACMB=3﹣t2+2t=﹣(t﹣1)2+4,
当t=1时,四边形ACMB的面积最大值为4,
此时M(1,﹣2).
15.如图,抛物线y=﹣x2+4x+5与x轴交于点A和点B,与y轴交于点C.
(1)求出A、B、C三点的坐标;
(2)将抛物线y=﹣x2+4x+5图象x轴上方部分沿x轴向下翻折,保留抛物线与x轴的交点和x轴下方图象,得到的新图象记作M,图象M与直线y=t恒有四个交点,从左到右四个交点依次记为D,E,F,G.若以EF为直径作圆,该圆记作图象N.
①在图象M上找一点P,使得△PAB的面积为3,求出点P的坐标;
②当图象N与x轴相离时,直接写出t的取值范围.
解:(1)令x=0,则y=5,
∴C(0,5),
令y=0,则﹣x2+4x+5=0,
解得x=5或x=﹣1,
∴A(﹣1,0),B(5,0);
(2)①设P点的纵坐标为m,
∵△PAB的面积为3,
∴6(﹣m)=3,
解得m=﹣1,
当﹣x2+4x+5=﹣1时,解得x=2+或x=2﹣,
∴P(2+,﹣1)或(2﹣,﹣1);
当﹣x2+4x+5=1时,解得x=2+或x=2﹣,
∴P(2+,﹣1)或(2﹣,﹣1);
综上所述:P点坐标为(2+,﹣1)或(2﹣,﹣1)或(2+,﹣1)或(2﹣,﹣1);
②∵y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴抛物线的顶点为(2,9),
∵图象M与直线y=t恒有四个交点,
∴﹣9<t≤0,
当﹣x2+4x+5=﹣t时,解得x=2+或x=2﹣,
∴E(2﹣,t),F(2+,t),
∴EF=2,
当=﹣t时,解得t=,
∵t<0,
∴t=,此时图象N与x轴相切,
∴﹣9<t<时,图象N与x轴相离.
同课章节目录
