2022—2023学年人教版数学七年级下册5.3 平行线的性质 随堂练习 (无答案)
文档属性
| 名称 | 2022—2023学年人教版数学七年级下册5.3 平行线的性质 随堂练习 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 88.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 21:33:14 | ||
图片预览

文档简介
5.3 平行线的性质(随堂练习)-2022年人教新版数学七年级下册
选择题
.下列命题为真命题的是( )
A.对角线相等的四边形是矩形
B.相似三角形面积之比等于相似比
C.顺次连接矩形各边的中点所得的四边形是正方形
D.两条直线被一组平行线所截,所得的对应线段成比例
.如图是一款手推车的平面示意图,其中AB∥CD,∠1=26°,∠2=74°,那么∠3的度数为( )
A.100° B.132° C.142° D.154°
.如图,a∥b,∠1=60°,则∠2的大小是( )
A.60° B.80° C.100° D.120°
.将45°的直角三角形纸片和矩形纸片按如图方式折叠放在一起,若∠1=31°,则∠2的度数为( )
A.10° B.14° C.20° D.31°
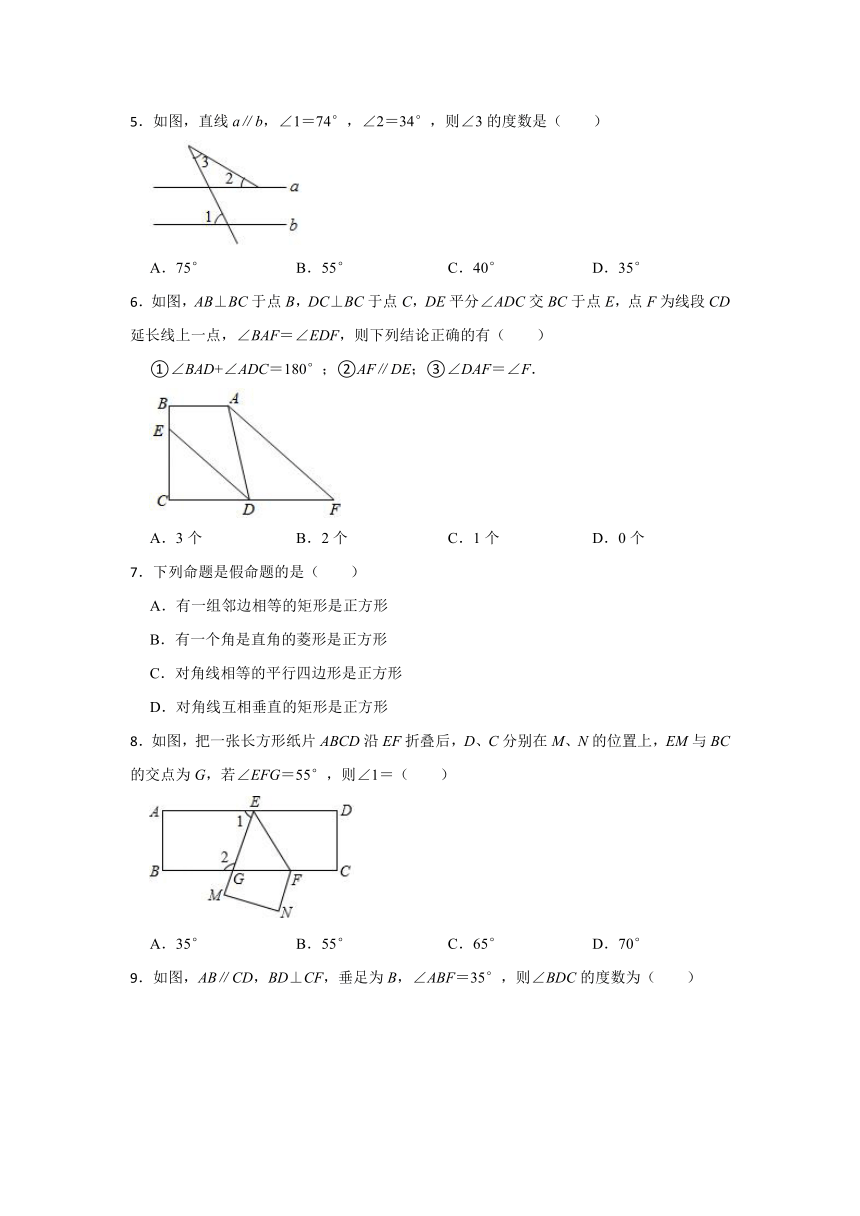
.如图,直线a∥b,∠1=74°,∠2=34°,则∠3的度数是( )
A.75° B.55° C.40° D.35°
.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个 B.2个 C.1个 D.0个
.下列命题是假命题的是( )
A.有一组邻边相等的矩形是正方形
B.有一个角是直角的菱形是正方形
C.对角线相等的平行四边形是正方形
D.对角线互相垂直的矩形是正方形
.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=55°,则∠1=( )
A.35° B.55° C.65° D.70°
.如图,AB∥CD,BD⊥CF,垂足为B,∠ABF=35°,则∠BDC的度数为( )
A.25° B.35° C.45° D.55°
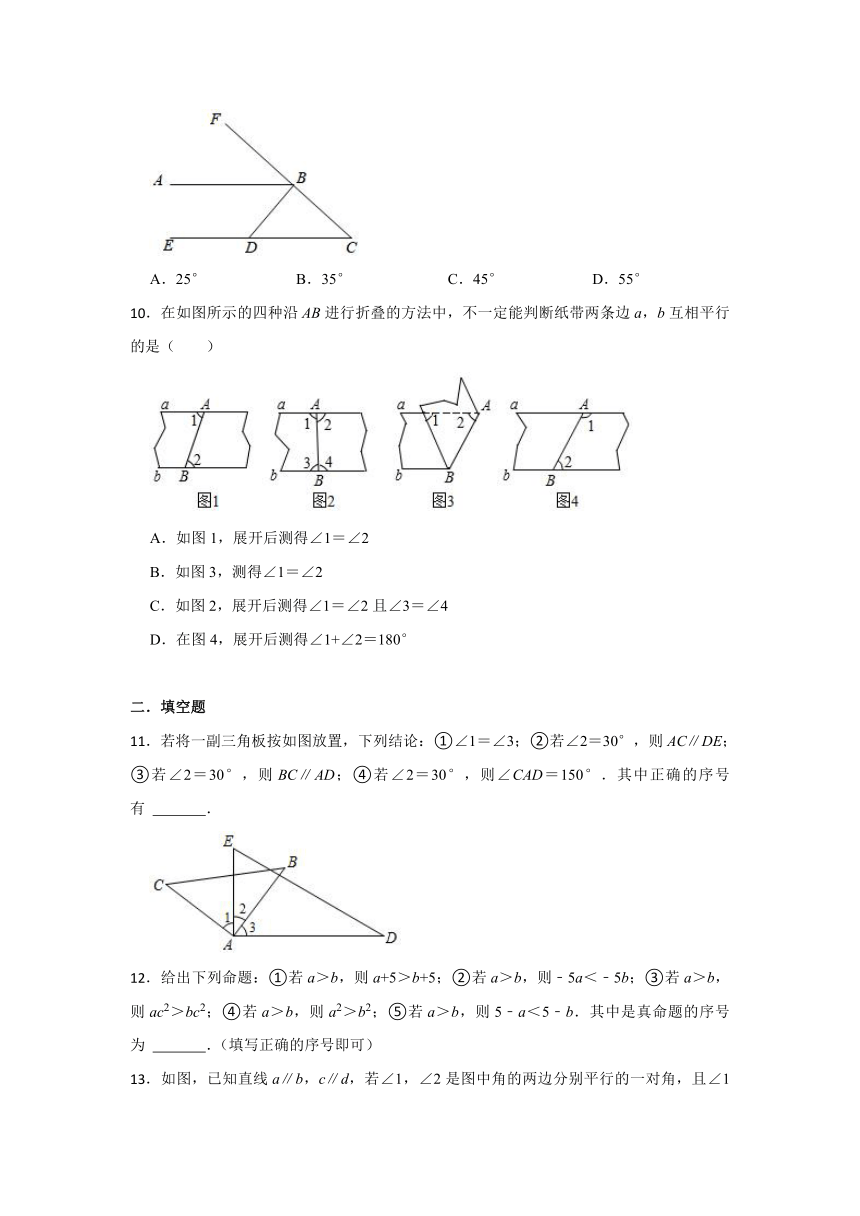
.在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2
B.如图3,测得∠1=∠2
C.如图2,展开后测得∠1=∠2且∠3=∠4
D.在图4,展开后测得∠1+∠2=180°
填空题
.若将一副三角板按如图放置,下列结论:①∠1=∠3;②若∠2=30°,则AC∥DE;③若∠2=30°,则BC∥AD;④若∠2=30°,则∠CAD=150°.其中正确的序号有 .
.给出下列命题:①若a>b,则a+5>b+5;②若a>b,则﹣5a<﹣5b;③若a>b,则ac2>bc2;④若a>b,则a2>b2;⑤若a>b,则5﹣a<5﹣b.其中是真命题的序号为 .(填写正确的序号即可)
.如图,已知直线a∥b,c∥d,若∠1,∠2是图中角的两边分别平行的一对角,且∠1的度数为(2x﹣3)°,∠2的度数为(3x﹣17)°,则x值为 .
.如图:已知点C、D是直线AB上两点,点E,F为平面内两点,且∠ACE+∠FDB=180°,CF平分∠ECB,EH⊥AB于点H交CF于点O.则下列结论正确的是: .
①EF∥AB;②CE∥DF;③∠FDB=2∠CFD;④∠FOE=∠CDF.
.如图,已知AB∥DC∥EO,∠1=70°,∠2=30°,OG平分∠BOD,则∠EOG= .
三.解答题
.如图,在四边形ABCD中,CE⊥AD于E.若( ),( ),则( ).
(1)从①CB=CD,②∠D+∠ABC=180°,③AC平分∠DAB,选择两个作为条件,剩下的一个作为结论,构成一个真命题.并说明理由.条件: , ,结论 ;
(2)在(1)的条件下,若AD=8,DE=2,CE=3,求△ABC的面积.
.如图,MN∥BC,BD⊥DC,∠1=∠2=60°,DC是∠NDE的平分线.
(1)AB与DE平行吗?请说明理由;
(2)试说明∠ABC=∠C;
(3)试说明BD是∠ABC的平分线.
.已知,如图,AD是△ABC的角平分线,DE∥AC,DE交AB于点E,DF∥AB,DF交AC于点F.
求证:DA平分∠EDF.
.在《几何原本》著作中,命题47:在直角三角形中,直角所对的边上的正方形等于夹直角两边上的正方形的和.古代人还没有发明勾股定理,他们如何证明这个命题是真命题.已知△ABC,∠BAC=90°;求证:以BC为边正方形的面积=以BA为边正方形的面积+以AC为边正方形的面积.
现请同学们求证:长方形BDQP的面积=正方形ABMN的面积.
.已知,如图,△ABC中,AB>AC,AF是角平分线,D是AB上一点,且AD=AC,DE∥BC交AC于E,求证:CD平分∠EDF.
选择题
.下列命题为真命题的是( )
A.对角线相等的四边形是矩形
B.相似三角形面积之比等于相似比
C.顺次连接矩形各边的中点所得的四边形是正方形
D.两条直线被一组平行线所截,所得的对应线段成比例
.如图是一款手推车的平面示意图,其中AB∥CD,∠1=26°,∠2=74°,那么∠3的度数为( )
A.100° B.132° C.142° D.154°
.如图,a∥b,∠1=60°,则∠2的大小是( )
A.60° B.80° C.100° D.120°
.将45°的直角三角形纸片和矩形纸片按如图方式折叠放在一起,若∠1=31°,则∠2的度数为( )
A.10° B.14° C.20° D.31°
.如图,直线a∥b,∠1=74°,∠2=34°,则∠3的度数是( )
A.75° B.55° C.40° D.35°
.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个 B.2个 C.1个 D.0个
.下列命题是假命题的是( )
A.有一组邻边相等的矩形是正方形
B.有一个角是直角的菱形是正方形
C.对角线相等的平行四边形是正方形
D.对角线互相垂直的矩形是正方形
.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=55°,则∠1=( )
A.35° B.55° C.65° D.70°
.如图,AB∥CD,BD⊥CF,垂足为B,∠ABF=35°,则∠BDC的度数为( )
A.25° B.35° C.45° D.55°
.在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2
B.如图3,测得∠1=∠2
C.如图2,展开后测得∠1=∠2且∠3=∠4
D.在图4,展开后测得∠1+∠2=180°
填空题
.若将一副三角板按如图放置,下列结论:①∠1=∠3;②若∠2=30°,则AC∥DE;③若∠2=30°,则BC∥AD;④若∠2=30°,则∠CAD=150°.其中正确的序号有 .
.给出下列命题:①若a>b,则a+5>b+5;②若a>b,则﹣5a<﹣5b;③若a>b,则ac2>bc2;④若a>b,则a2>b2;⑤若a>b,则5﹣a<5﹣b.其中是真命题的序号为 .(填写正确的序号即可)
.如图,已知直线a∥b,c∥d,若∠1,∠2是图中角的两边分别平行的一对角,且∠1的度数为(2x﹣3)°,∠2的度数为(3x﹣17)°,则x值为 .
.如图:已知点C、D是直线AB上两点,点E,F为平面内两点,且∠ACE+∠FDB=180°,CF平分∠ECB,EH⊥AB于点H交CF于点O.则下列结论正确的是: .
①EF∥AB;②CE∥DF;③∠FDB=2∠CFD;④∠FOE=∠CDF.
.如图,已知AB∥DC∥EO,∠1=70°,∠2=30°,OG平分∠BOD,则∠EOG= .
三.解答题
.如图,在四边形ABCD中,CE⊥AD于E.若( ),( ),则( ).
(1)从①CB=CD,②∠D+∠ABC=180°,③AC平分∠DAB,选择两个作为条件,剩下的一个作为结论,构成一个真命题.并说明理由.条件: , ,结论 ;
(2)在(1)的条件下,若AD=8,DE=2,CE=3,求△ABC的面积.
.如图,MN∥BC,BD⊥DC,∠1=∠2=60°,DC是∠NDE的平分线.
(1)AB与DE平行吗?请说明理由;
(2)试说明∠ABC=∠C;
(3)试说明BD是∠ABC的平分线.
.已知,如图,AD是△ABC的角平分线,DE∥AC,DE交AB于点E,DF∥AB,DF交AC于点F.
求证:DA平分∠EDF.
.在《几何原本》著作中,命题47:在直角三角形中,直角所对的边上的正方形等于夹直角两边上的正方形的和.古代人还没有发明勾股定理,他们如何证明这个命题是真命题.已知△ABC,∠BAC=90°;求证:以BC为边正方形的面积=以BA为边正方形的面积+以AC为边正方形的面积.
现请同学们求证:长方形BDQP的面积=正方形ABMN的面积.
.已知,如图,△ABC中,AB>AC,AF是角平分线,D是AB上一点,且AD=AC,DE∥BC交AC于E,求证:CD平分∠EDF.
