2022—2023学年北师大版数学八年级上册第3章 位置与坐标 提升训练题(含解析)
文档属性
| 名称 | 2022—2023学年北师大版数学八年级上册第3章 位置与坐标 提升训练题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 84.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 00:00:00 | ||
图片预览




文档简介
第3章 位置与坐标(提升训练题)-北师大版八年级上册
一.选择题
.下列各点在第四象限内的点是( )
A.(2,﹣) B.(﹣2,3) C.(﹣,﹣6) D.(2,3)
.经过点P(﹣4,3)垂直于x轴的直线可以表示为( )
A.直线 x=3 B.直线y=﹣4 C.直线x=﹣4 D.直线 y=3
.在平面直角坐标系中,点A的坐标为(﹣1,3),点B的坐标为(5,3),则线段AB上任意一点的坐标可表示为( )
A.(3,x)(﹣1≤x≤5) B.(x,3)(﹣1≤x≤5)
C.(3,x)(﹣5≤x≤1) D.(x,3)(﹣5≤x≤1)
.若点P(a,2)在第二象限内,则点Q(﹣a,0)在( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
.若点P(﹣3,b)在第二象限内,则b可以是( )
A.﹣2 B.﹣1 C.0 D.2
.根据下列表述,不能确定具体位置的是( )
A.某电影院1号厅的3排4座
B.石家庄市和平路85号
C.某灯落南偏西30°方向
D.东经108°,北纬53°
.在平面直角坐标系中,若点A(m+2,m)在y轴上,则点B(m+5,m﹣1)的坐标为( )
A.(3,﹣3) B.(5,﹣1) C.(3,3) D.(5,1)
.在平面直角坐标系中,若点(3,2)与点(m,﹣2)关于原点对称,则m的值是( )
A.2 B.﹣2 C.3 D.﹣3
.在平面直角坐标系中,位于第四象限的点的坐标是( )
A.(﹣2,1) B.(﹣1,﹣1) C.(0,3) D.(1,﹣2)
.如图,在平面直角坐标系中,A(﹣1,1),B(﹣1,﹣2),C(3,﹣2),D(3,1),一只瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A循环爬行,问第2022秒瓢虫在( )处.
A.(3,﹣2) B.(﹣1,﹣1) C.(1,﹣2) D.(1,1)
二.填空题
.已知y轴上有一动点A(0,a),点B(5,9)是平面直角坐标系中的一点,则线段AB长度的最小值为 .
.已知线段AB∥y轴,点A(1,﹣3),B(m,n),且AB=5时,点B的坐标为 .
.电影院里5排6座记作(5,6),则3排7座记作 .
.在平面直角坐标系中,若点A、B的坐标分别为(0,2)和(n,n+4),则线段AB长的最小值为 .
.直线AB经过两点A(1,3)、B(4,6),该直线与x轴所夹的锐角为a,则a值为 .
三.解答题
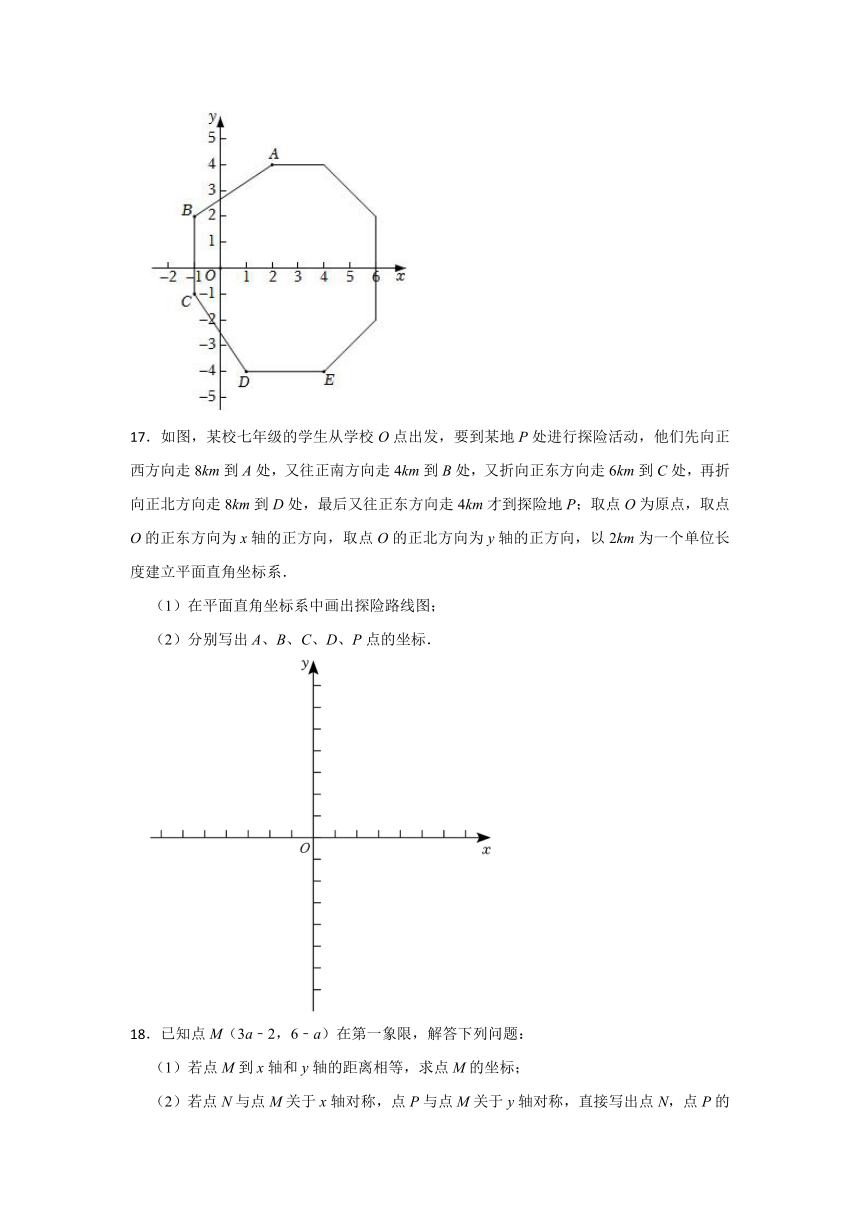
.如图,(1)请说出A,B,C,D,E五点的坐标.
(2)请你观察B,C两点的坐标,你发现什么了吗?线段BC与y轴有什么关系?与x轴呢?由此你能得出什么结论?
(3)进一步观察D,E两点的坐标你发现了什么?
.如图,某校七年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.
(1)在平面直角坐标系中画出探险路线图;
(2)分别写出A、B、C、D、P点的坐标.
.已知点M(3a﹣2,6﹣a)在第一象限,解答下列问题:
(1)若点M到x轴和y轴的距离相等,求点M的坐标;
(2)若点N与点M关于x轴对称,点P与点M关于y轴对称,直接写出点N,点P的坐标.
.已知点P(2a+3,a﹣4).
(1)若点P在x轴上,求点P的坐标;
(2)若点Q(3,2b)在第一象限,PQ∥y轴,且PQ=10,求点Q的坐标;
(3)若点P到x轴的距离比到y轴的距离多2,求点P的坐标.
.对于平面直角坐标系中的点P(a,b),若点P′的坐标为(a+,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k系培圣点”.例如:P(1,4)的“2系培呈点”为P′(1+,2×1+4),P′(3,6).
(1)点P(﹣1,6)的“3系培圣点”P′的坐标为 .
(2)若点P(x,0),x为正整数,点P的“k系培圣点”为P′点,且PP′+OP+2k=7,k为正整数,求k的值.
(3)若关于x的分式方程=2无解,求m的值.
参考答案与试题解析
一.选择题
.【解答】解:A.(2,﹣)在第四象限,故本选项符合题意;
B.(﹣2,3)在第二象限,故本选项不符合题意;
C.(﹣,﹣6)在第三象限,故本选项不符合题意;
D.(2,3)在第一象限,故本选项不符合题意;
故选:A.
.【解答】解:经过点P(﹣4,3)且垂直于x轴的直线可以表示为直线x=﹣4.
故选:C.
.【解答】解:∵点A的坐标为(﹣1,3),点B的坐标为(5,3),A、B两点纵坐标都为3,
∴AB∥x轴,
∴线段AB上任意一点的坐标可表示为(x,3)(﹣1≤x≤5),
故选:B.
.【解答】解:∵点P(a,2)在第二象限内,
∴a<0,
∴﹣a>0,
∴Q(﹣a,0)在x轴正半轴上,
故选:A.
.【解答】解:∵点P(﹣3,b)在第二象限内,
∴b>0,
∵﹣2<0,﹣1<0,0=0,2>0,
∴b可以为2,
故选:D.
.【解答】解:A.某电影院1号厅的3排4座,能确定具体位置,故此选项不合题意;
B.石家庄市和平路85号,能确定具体位置,故此选项不合题意;
C.某灯落南偏西30°方向,不能确定具体位置,故此选项符合题意;
D.东经108°,北纬53°,可以确定具体位置,故此选项不合题意;
故选:C.
.【解答】解:∵点A(m+2,m)在y轴上,
∴m+2=0,
∴m=﹣2,
∵B(m+5,m﹣1),
∴B(3,﹣3),
故选:A.
.【解答】解:∵点(3,2)与点(m,﹣2)关于原点对称,
∴m=﹣3,
故选:D.
.【解答】解:A、(﹣2,1)位于第二象限,故此选项不符合题意;
B、(﹣1,﹣1)位于第三象限,故此选项不符合题意;
C、(0,3)位于y轴上,故此选项不符合题意;
D、(1,﹣2)位于第四象限,故此选项符合题意.
故选:D.
.【解答】解:∵A(﹣1,1),B(﹣1,﹣2),C(3,﹣2),D(3,1),
∴AB=CD=3,AD=BC=4,
∴C矩形ABCD=2(AB+AD)=14,
∵14÷2=7(秒),
∴瓢虫爬行一周需要7秒,
∴2022÷7=288……6,
∴6×2=12,
∴12﹣3﹣4﹣3=2,
∴第2022秒瓢虫在(1,1)处.
故选:D.
二.填空题
.【解答】解:∵点的横坐标的绝对值就是到y轴的距离,
∴点B(5,9)到y轴的距离是5.
∴则线段AB长度的最小值为5.
故答案为:5.
.【解答】解:∵AB∥y轴,点A的坐标为(1,﹣3),
∴点B的横坐标为1,
∵AB=5,
∴点B在点A的上方时,点B的纵坐标为2,点B的坐标为(1,2),
点B在点A的下方时,点B的纵坐标为﹣8,点B的坐标为(1,﹣8),
综上所述,点B的坐标为(1,2)或(1,﹣8).
故答案为:(1,2)或(1,﹣8).
.【解答】解:∵电影院里5排6座记作(5,6),
∴3排7座记作(3,7),
故答案为:(3,7).
.【解答】解:如图,点B在直线y=x+4的图象上,当AB⊥CD时,线段AB最短,
对于y=x+4,
当x=0时,y=4,
当y=0时,x=﹣4,
∴A(﹣4,0),C(0,4),
∴OC=OD=4,
∴AC=OC﹣OA=4﹣2=2,∠C=∠D=45°,
∵AB⊥CD,
∴∠C=∠CAB=45°,
∴AB=BC,
在Rt△ABC中,
AB2+BC2=AC2,
∴2AB2=22,
∴AB=.
故答案为:.
.【解答】解:设这条直线的解析式为y=kx+b(k≠0).
由题意得
∴
∴这条直线的斜率为k=1.
∴该直线与x轴所夹的锐角为a=45°.
故答案为:45°.
三.解答题
.【解答】解:(1)A,B,C,D,E五点的坐标分别为(2,4),(﹣1,2),(﹣1,﹣1),(1,﹣4),(4,﹣4).
(2)通过观察B,C两点的坐标,发现B,C两点的横坐标相同,线段BC与y轴平行,与x轴垂直.
由此可得出:若一直线上的所有点的横坐标均相同,则此直线与y轴平行(或就是y轴),也可以说是与x轴垂直.
(3)通过观察D,E两点的坐标,发现D,E两点的纵坐标相同,线段DE与x轴平行,与y轴垂直.
由此可得出若一直线上的所有点的纵坐标均相同,则此直线与x轴平行(或就是x轴),也可以说是与y轴垂直.
.【解答】解:(1)如图所示;
(
(2)A(﹣4,0);B(﹣4,﹣2);C(﹣1,﹣2);D(﹣1,2);P(1,2).
.【解答】解:(1)由题意得:
3a﹣2=6﹣a,
3a+a=6+2,
4a=8,
a=2,
当a=2时,3a﹣2=4,6﹣a=4,
∴点M的坐标为(4,4);
(2)∵点N与点M关于x轴对称,
∴点N的坐标为(3a﹣2,a﹣6);
∵点P与点M关于y轴对称,
∴点P的坐标为(2﹣3a,6﹣a);
∴点N的坐标为(3a﹣2,a﹣6);点P的坐标为(2﹣3a,6﹣a).
.【解答】解:(1)∵点P在x轴上,
∴a﹣4=0,
∴a=4,
∴2a+3=2×4+3=11,
∴点P的坐标为(11,0);
(2)∵PQ∥y轴,
∴2a+3=3,解得a=0,
∴点P(3,﹣4).
∵点Q(3,2b)在第一象限,且PQ=10,
∴2b﹣(﹣4)=10,
∴2b=6,
∴点Q的坐标(3,6);
(3)∵点P到x轴的距离比到y轴的距离多2,
∴|a﹣4|=|2a+3|+2,
①当a>4时,a﹣4=2a+3+2,
解得a=﹣9,
∴﹣9<4,
a=﹣9不合题意,舍去;
②当﹣<a<4时,4﹣a=2a+3+2,
解得a=﹣,
∴点P的坐标为(,﹣);
③当a<﹣时,4﹣a=﹣2a﹣3+2,
解得a=﹣5;
∴点P的坐标为(﹣7,﹣9);
综上所述,点P的坐标为(,﹣)或(﹣7,﹣9).
.【解答】解:(1)当a=﹣1,b=6,k=3时,﹣1+=1,3×(﹣1)+6=3,
∴点P(﹣1,6)的“3系培圣点”P'的坐标为(1,3),
故答案为:(1,3);
(2)∵点P(x,0),x为正整数,点P的“k系培圣点”为P′点,
∴P′(x,kx),
∴PP′==|kx|,OP=x,
∴|kx|+x+2k=7,
即kx+x+2k=7或﹣kx+x+2k=7,
解得:k=或,
∵k为正整数,
∴k=2或6;
(3)给分式方程两边同时乘以(x﹣3)(x+3),得,
mx2+(12+3m)x+36=0,
∵上述分式方程无解,
∴x2﹣9=0,即x=3或x=﹣3,
①当x=3时,代入mx2+(12+3m)x+36=0,则m=﹣4;
②当x=﹣3时,代入mx2+(12+3m)x+36=0,则9m﹣36﹣9m+36=0(不合题意,舍去),
综上,m=﹣4.
一.选择题
.下列各点在第四象限内的点是( )
A.(2,﹣) B.(﹣2,3) C.(﹣,﹣6) D.(2,3)
.经过点P(﹣4,3)垂直于x轴的直线可以表示为( )
A.直线 x=3 B.直线y=﹣4 C.直线x=﹣4 D.直线 y=3
.在平面直角坐标系中,点A的坐标为(﹣1,3),点B的坐标为(5,3),则线段AB上任意一点的坐标可表示为( )
A.(3,x)(﹣1≤x≤5) B.(x,3)(﹣1≤x≤5)
C.(3,x)(﹣5≤x≤1) D.(x,3)(﹣5≤x≤1)
.若点P(a,2)在第二象限内,则点Q(﹣a,0)在( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
.若点P(﹣3,b)在第二象限内,则b可以是( )
A.﹣2 B.﹣1 C.0 D.2
.根据下列表述,不能确定具体位置的是( )
A.某电影院1号厅的3排4座
B.石家庄市和平路85号
C.某灯落南偏西30°方向
D.东经108°,北纬53°
.在平面直角坐标系中,若点A(m+2,m)在y轴上,则点B(m+5,m﹣1)的坐标为( )
A.(3,﹣3) B.(5,﹣1) C.(3,3) D.(5,1)
.在平面直角坐标系中,若点(3,2)与点(m,﹣2)关于原点对称,则m的值是( )
A.2 B.﹣2 C.3 D.﹣3
.在平面直角坐标系中,位于第四象限的点的坐标是( )
A.(﹣2,1) B.(﹣1,﹣1) C.(0,3) D.(1,﹣2)
.如图,在平面直角坐标系中,A(﹣1,1),B(﹣1,﹣2),C(3,﹣2),D(3,1),一只瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A循环爬行,问第2022秒瓢虫在( )处.
A.(3,﹣2) B.(﹣1,﹣1) C.(1,﹣2) D.(1,1)
二.填空题
.已知y轴上有一动点A(0,a),点B(5,9)是平面直角坐标系中的一点,则线段AB长度的最小值为 .
.已知线段AB∥y轴,点A(1,﹣3),B(m,n),且AB=5时,点B的坐标为 .
.电影院里5排6座记作(5,6),则3排7座记作 .
.在平面直角坐标系中,若点A、B的坐标分别为(0,2)和(n,n+4),则线段AB长的最小值为 .
.直线AB经过两点A(1,3)、B(4,6),该直线与x轴所夹的锐角为a,则a值为 .
三.解答题
.如图,(1)请说出A,B,C,D,E五点的坐标.
(2)请你观察B,C两点的坐标,你发现什么了吗?线段BC与y轴有什么关系?与x轴呢?由此你能得出什么结论?
(3)进一步观察D,E两点的坐标你发现了什么?
.如图,某校七年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.
(1)在平面直角坐标系中画出探险路线图;
(2)分别写出A、B、C、D、P点的坐标.
.已知点M(3a﹣2,6﹣a)在第一象限,解答下列问题:
(1)若点M到x轴和y轴的距离相等,求点M的坐标;
(2)若点N与点M关于x轴对称,点P与点M关于y轴对称,直接写出点N,点P的坐标.
.已知点P(2a+3,a﹣4).
(1)若点P在x轴上,求点P的坐标;
(2)若点Q(3,2b)在第一象限,PQ∥y轴,且PQ=10,求点Q的坐标;
(3)若点P到x轴的距离比到y轴的距离多2,求点P的坐标.
.对于平面直角坐标系中的点P(a,b),若点P′的坐标为(a+,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k系培圣点”.例如:P(1,4)的“2系培呈点”为P′(1+,2×1+4),P′(3,6).
(1)点P(﹣1,6)的“3系培圣点”P′的坐标为 .
(2)若点P(x,0),x为正整数,点P的“k系培圣点”为P′点,且PP′+OP+2k=7,k为正整数,求k的值.
(3)若关于x的分式方程=2无解,求m的值.
参考答案与试题解析
一.选择题
.【解答】解:A.(2,﹣)在第四象限,故本选项符合题意;
B.(﹣2,3)在第二象限,故本选项不符合题意;
C.(﹣,﹣6)在第三象限,故本选项不符合题意;
D.(2,3)在第一象限,故本选项不符合题意;
故选:A.
.【解答】解:经过点P(﹣4,3)且垂直于x轴的直线可以表示为直线x=﹣4.
故选:C.
.【解答】解:∵点A的坐标为(﹣1,3),点B的坐标为(5,3),A、B两点纵坐标都为3,
∴AB∥x轴,
∴线段AB上任意一点的坐标可表示为(x,3)(﹣1≤x≤5),
故选:B.
.【解答】解:∵点P(a,2)在第二象限内,
∴a<0,
∴﹣a>0,
∴Q(﹣a,0)在x轴正半轴上,
故选:A.
.【解答】解:∵点P(﹣3,b)在第二象限内,
∴b>0,
∵﹣2<0,﹣1<0,0=0,2>0,
∴b可以为2,
故选:D.
.【解答】解:A.某电影院1号厅的3排4座,能确定具体位置,故此选项不合题意;
B.石家庄市和平路85号,能确定具体位置,故此选项不合题意;
C.某灯落南偏西30°方向,不能确定具体位置,故此选项符合题意;
D.东经108°,北纬53°,可以确定具体位置,故此选项不合题意;
故选:C.
.【解答】解:∵点A(m+2,m)在y轴上,
∴m+2=0,
∴m=﹣2,
∵B(m+5,m﹣1),
∴B(3,﹣3),
故选:A.
.【解答】解:∵点(3,2)与点(m,﹣2)关于原点对称,
∴m=﹣3,
故选:D.
.【解答】解:A、(﹣2,1)位于第二象限,故此选项不符合题意;
B、(﹣1,﹣1)位于第三象限,故此选项不符合题意;
C、(0,3)位于y轴上,故此选项不符合题意;
D、(1,﹣2)位于第四象限,故此选项符合题意.
故选:D.
.【解答】解:∵A(﹣1,1),B(﹣1,﹣2),C(3,﹣2),D(3,1),
∴AB=CD=3,AD=BC=4,
∴C矩形ABCD=2(AB+AD)=14,
∵14÷2=7(秒),
∴瓢虫爬行一周需要7秒,
∴2022÷7=288……6,
∴6×2=12,
∴12﹣3﹣4﹣3=2,
∴第2022秒瓢虫在(1,1)处.
故选:D.
二.填空题
.【解答】解:∵点的横坐标的绝对值就是到y轴的距离,
∴点B(5,9)到y轴的距离是5.
∴则线段AB长度的最小值为5.
故答案为:5.
.【解答】解:∵AB∥y轴,点A的坐标为(1,﹣3),
∴点B的横坐标为1,
∵AB=5,
∴点B在点A的上方时,点B的纵坐标为2,点B的坐标为(1,2),
点B在点A的下方时,点B的纵坐标为﹣8,点B的坐标为(1,﹣8),
综上所述,点B的坐标为(1,2)或(1,﹣8).
故答案为:(1,2)或(1,﹣8).
.【解答】解:∵电影院里5排6座记作(5,6),
∴3排7座记作(3,7),
故答案为:(3,7).
.【解答】解:如图,点B在直线y=x+4的图象上,当AB⊥CD时,线段AB最短,
对于y=x+4,
当x=0时,y=4,
当y=0时,x=﹣4,
∴A(﹣4,0),C(0,4),
∴OC=OD=4,
∴AC=OC﹣OA=4﹣2=2,∠C=∠D=45°,
∵AB⊥CD,
∴∠C=∠CAB=45°,
∴AB=BC,
在Rt△ABC中,
AB2+BC2=AC2,
∴2AB2=22,
∴AB=.
故答案为:.
.【解答】解:设这条直线的解析式为y=kx+b(k≠0).
由题意得
∴
∴这条直线的斜率为k=1.
∴该直线与x轴所夹的锐角为a=45°.
故答案为:45°.
三.解答题
.【解答】解:(1)A,B,C,D,E五点的坐标分别为(2,4),(﹣1,2),(﹣1,﹣1),(1,﹣4),(4,﹣4).
(2)通过观察B,C两点的坐标,发现B,C两点的横坐标相同,线段BC与y轴平行,与x轴垂直.
由此可得出:若一直线上的所有点的横坐标均相同,则此直线与y轴平行(或就是y轴),也可以说是与x轴垂直.
(3)通过观察D,E两点的坐标,发现D,E两点的纵坐标相同,线段DE与x轴平行,与y轴垂直.
由此可得出若一直线上的所有点的纵坐标均相同,则此直线与x轴平行(或就是x轴),也可以说是与y轴垂直.
.【解答】解:(1)如图所示;
(
(2)A(﹣4,0);B(﹣4,﹣2);C(﹣1,﹣2);D(﹣1,2);P(1,2).
.【解答】解:(1)由题意得:
3a﹣2=6﹣a,
3a+a=6+2,
4a=8,
a=2,
当a=2时,3a﹣2=4,6﹣a=4,
∴点M的坐标为(4,4);
(2)∵点N与点M关于x轴对称,
∴点N的坐标为(3a﹣2,a﹣6);
∵点P与点M关于y轴对称,
∴点P的坐标为(2﹣3a,6﹣a);
∴点N的坐标为(3a﹣2,a﹣6);点P的坐标为(2﹣3a,6﹣a).
.【解答】解:(1)∵点P在x轴上,
∴a﹣4=0,
∴a=4,
∴2a+3=2×4+3=11,
∴点P的坐标为(11,0);
(2)∵PQ∥y轴,
∴2a+3=3,解得a=0,
∴点P(3,﹣4).
∵点Q(3,2b)在第一象限,且PQ=10,
∴2b﹣(﹣4)=10,
∴2b=6,
∴点Q的坐标(3,6);
(3)∵点P到x轴的距离比到y轴的距离多2,
∴|a﹣4|=|2a+3|+2,
①当a>4时,a﹣4=2a+3+2,
解得a=﹣9,
∴﹣9<4,
a=﹣9不合题意,舍去;
②当﹣<a<4时,4﹣a=2a+3+2,
解得a=﹣,
∴点P的坐标为(,﹣);
③当a<﹣时,4﹣a=﹣2a﹣3+2,
解得a=﹣5;
∴点P的坐标为(﹣7,﹣9);
综上所述,点P的坐标为(,﹣)或(﹣7,﹣9).
.【解答】解:(1)当a=﹣1,b=6,k=3时,﹣1+=1,3×(﹣1)+6=3,
∴点P(﹣1,6)的“3系培圣点”P'的坐标为(1,3),
故答案为:(1,3);
(2)∵点P(x,0),x为正整数,点P的“k系培圣点”为P′点,
∴P′(x,kx),
∴PP′==|kx|,OP=x,
∴|kx|+x+2k=7,
即kx+x+2k=7或﹣kx+x+2k=7,
解得:k=或,
∵k为正整数,
∴k=2或6;
(3)给分式方程两边同时乘以(x﹣3)(x+3),得,
mx2+(12+3m)x+36=0,
∵上述分式方程无解,
∴x2﹣9=0,即x=3或x=﹣3,
①当x=3时,代入mx2+(12+3m)x+36=0,则m=﹣4;
②当x=﹣3时,代入mx2+(12+3m)x+36=0,则9m﹣36﹣9m+36=0(不合题意,舍去),
综上,m=﹣4.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
