2022—2023学年北师大版数学七年级上册第3章 整式及其加减(含解析)
文档属性
| 名称 | 2022—2023学年北师大版数学七年级上册第3章 整式及其加减(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 115.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 21:36:47 | ||
图片预览




文档简介
第3章 整式及其加减(压轴题 )-北师大版七年级上册
一.选择题
1.按照如图所示的计算程序,若x=2,则输出的结果是( )
A.16 B.26 C.﹣16 D.﹣26
2.某楼盘在今年国庆节期间,为了增加销售业绩,提高销售量,该楼盘在原单价为a元/平方米的基础上降价10%,则降价后的单价为( )元/平方米.
A.(1+10%)a B.(1﹣10%)a C.1+10%a D.10%a
3.甲、乙、丙三家商店对一种定价相同的文具开展促销活动.甲商店一次性降价30%;乙商店连续两次降价15%;丙商店先降价20%后又降价10%.若小雪准备在促销活动中,购买此种文具,则下列说法中,正确的是( )
A.小雪到甲商店购买这种文具更合算
B.小雪到乙商店购买这种文具更合算
C.小雪到丙商店购买这种文具更合算
D.在促销活动中,三家商店的这种文具售价相同,小雪可任选一家购买
4.若(2x﹣1)6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,则a6﹣a5+a4﹣a3+a2﹣a1的值为( )
A.0 B.1 C.728 D.729
5.如图,直线AB、CD相交于点O,“阿基米德曲线”从点O开始生成,如果将该曲线与每条射线的交点依次标记为2,﹣4,6,﹣8,10,﹣12,….那么标记“2022”的点在射线( )上.
A.OA B.OB C.OC D.OD
6.若代数式a2﹣3a的值是4,则a2﹣a﹣5的值是( )
A.﹣2 B.﹣3 C.﹣4 D.﹣5
x … ﹣1 0 1 2 …
kx+b … ﹣1 1 3 5 …
7.代数式kx+b当中,当x取值分别为﹣1,0,1,2时,对应代数式的值如下表:
则﹣2k﹣b的值为( )
A.﹣1 B.2 C.﹣3 D.﹣5
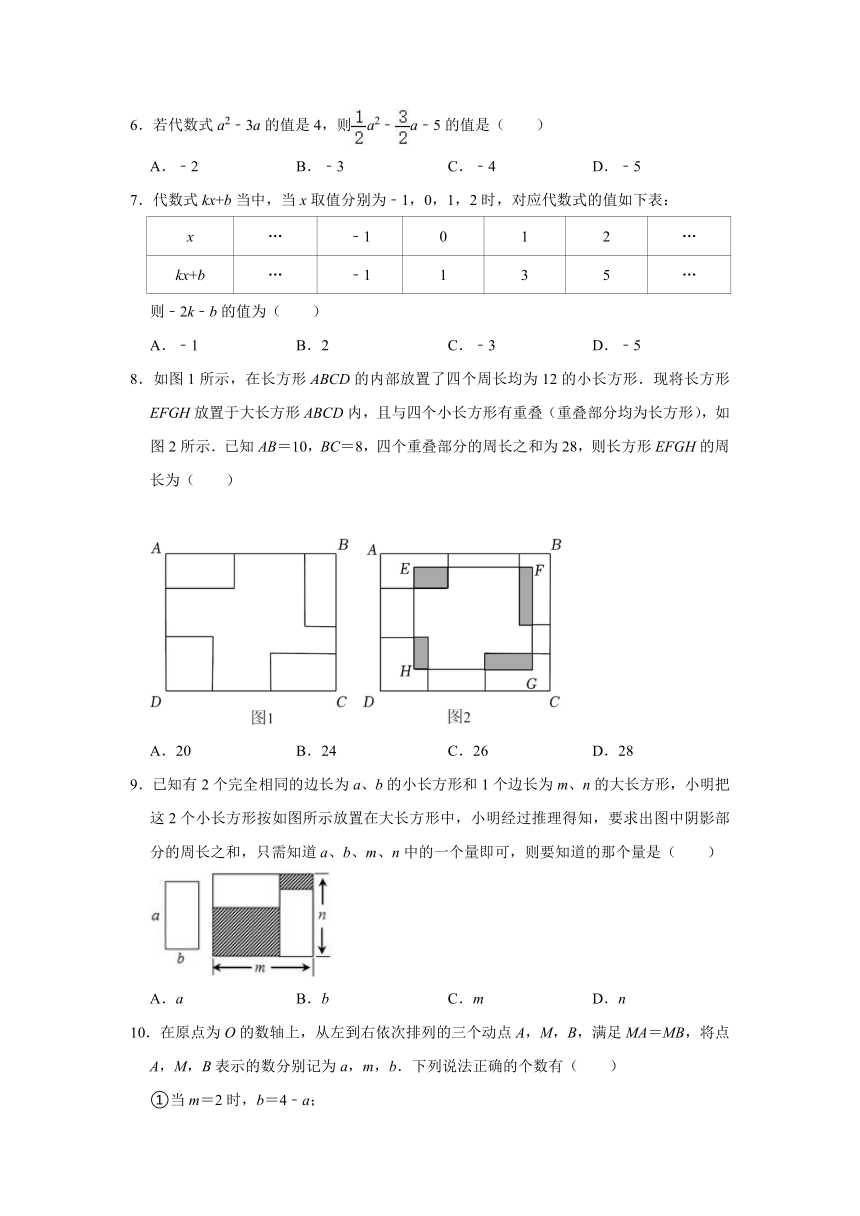
8.如图1所示,在长方形ABCD的内部放置了四个周长均为12的小长方形.现将长方形EFGH放置于大长方形ABCD内,且与四个小长方形有重叠(重叠部分均为长方形),如图2所示.已知AB=10,BC=8,四个重叠部分的周长之和为28,则长方形EFGH的周长为( )
A.20 B.24 C.26 D.28
9.已知有2个完全相同的边长为a、b的小长方形和1个边长为m、n的大长方形,小明把这2个小长方形按如图所示放置在大长方形中,小明经过推理得知,要求出图中阴影部分的周长之和,只需知道a、b、m、n中的一个量即可,则要知道的那个量是( )
A.a B.b C.m D.n
10.在原点为O的数轴上,从左到右依次排列的三个动点A,M,B,满足MA=MB,将点A,M,B表示的数分别记为a,m,b.下列说法正确的个数有( )
①当m=2时,b=4﹣a;
②当m=5时,若a为奇数,且5<b≤8,则a=3或5;
③若b=8,BM=3OM,则m=2;
④当m=3,b=4时,将点B水平右移3个单位至点B1,再将点B1水平右移3个单位至点B2,以此类推,…且满足MAn=MBn,则数轴上与B2022对应的点A2022表示的数为﹣6064.
A.1 B.2 C.3 D.4
二.填空题
.已知W=ma+mb+mc,当a=19.7,b=32.5,c=35.8,m=2.5时,W= .
.已知代数式x4+ax3+3x2+5x3﹣7x2﹣bx2+6x﹣2合并同类项后不含x3,x2项,则2a+3b的值 .
.我们定义:f(x)=,则f(10)= ;
f()+f()+…+f()+f(1)+f(0)+f(1)+f(2)+…+f(19)+f(20)= .
.一个圆的半径是rcm,如果它的半径增加3cm,那么它的面积增加 cm2.
.立信初一年级周二体锻课站队时,有三个人数一样多的小组(假设人数足够多)分别记为A、B、C三个小组,依次完成以下三个步骤:第一步,A组二个人去B组;第二步,C组三个人去B组;第三步,A组还有几个人,B组就去多少人到A组.请你确定,最终B组人数为 人.
三.解答题
.在计算题目:“已知:M=3x2﹣4x+2,N=■,求2M﹣N”时,嘉淇把“2M﹣N”看成“M﹣2N”,得到的计算结果是﹣x2+4x﹣4.
(1)求整式N;
(2)判断2M﹣N的化简结果是否能为负数,并说明理由.
.化简求值
已知A=2x2+3xy﹣2x﹣1,B=﹣x2+xy+x,
(1)化简3A+6B;
(2)当x=﹣2,y=1时,求代数式3A+6B的值.
.钟山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米,现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米.
(1)整改后A园区的长为 ,宽为 ;(用代数式表示)
(2)若整改后A园区的长比宽多350米,且整改后两园区的周长之和为980米,求x、y的值.
.某学校初中部和小学部一起在操场做课间操,初中部排成长方形.每排(4a﹣b)人站成(4a+b)排;小学部排成一个边长2(a+b)的方阵.
(1)初中部比小学部多多少人?(用字母a,b表示)
(2)当a=10,b=2时,请计算出此时初中部比小学部多多少人.
.如图,长为40,宽为x的大长方形被分割为9小块,除阴影A,B两块外,其余7块是形状、大小完全相同的小长方形,其较短一边长为y.
(1)分别用含x,y的代数式表示阴影A,B两块的周长,并计算阴影A,B两块的周长和.
(2)分别用含x,y的代数式表示阴影A,B两块的面积,并计算阴影A,B的面积差.
(3)当y取何值时,阴影A与阴影B的面积差不会随着x的变化而变化,并求出这个值.
参考答案与试题解析
一.选择题
1.【解答】解:当x=2时,10﹣x2=10﹣4=6>0,不合题意;
当x=6时,10﹣x2=10﹣36=﹣26<0,符合题意,
故选:D.
2.【解答】解:由题意得,降价后的单价为(1﹣10%)a,
故选:B.
3.【解答】解:在甲商店买这种文具需要:
1×(1﹣30%)
=1×70%
=0.7,
在乙商店买这种文具需要:
1×(1﹣15%)×(1﹣15%)
=1×85%×85%
=0.7225,
在丙商店买这种文具需要:
1×(1﹣20%)×(1﹣10%)
=1×80%×90%
=0.72,
因为0.7<0.72<0.7225,
所以小雪购买这种文具应该去的商店是甲.
故选:A.
4.【解答】解:把x=0代入,得:(﹣1)6=a0
把x=﹣1代入得:
[2×(﹣1)﹣1]6=a6﹣a5+a4﹣a3+a2﹣a1+a0,
(﹣3)6=a6﹣a5+a4﹣a3+a2﹣a1+1,
∴a6﹣a5+a4﹣a3+a2﹣a1=728,
故选:C.
.【解答】解:观察图形的变化可知:
奇数项:2、6、10、14…4n﹣2(n为正整数);
偶数项:﹣4、﹣8、﹣12、﹣16…﹣4n.
∵2022是奇数项,
∴4n﹣2=2022,
∴n=506.
∵每四条射线为一组,OC为始边,
∴506÷4=126…2.
∴标记为“2022”的点在射线OB上.
故选:B.
.【解答】解:∵代数式a2﹣3a的值为4,
∴a2﹣3a=4,
∴
=(a2﹣3a)﹣5
=
=2﹣5
=﹣3.
故选:B.
.【解答】解:∵x=2时,代数式2k+b=5,
∴﹣2k﹣b=﹣(2k+b)=﹣5.
故选:D.
.【解答】解:如图:
∵AB=10,BC=8,
∴AB+BC+CD+DA=2(AB+BC)=36,
∵长方形ABCD的内部放置了四个周长均为12的小长方形,
∴AN+AO=BM+BL=CK+CJ=DI+PD=×12=6,
∴(AB+BC+CD+DA)﹣(AN+AO)﹣(BM+BL)﹣(CK+CJ)﹣(DI+PD)=36﹣6﹣6﹣6﹣6=12,即MN+LK+IJ+OP=12,
∴XW+UV+ST+QR=12,
∵四个重叠部分的周长之和为28,
∴EX+EQ+RH+HS+TG+GU+FV+WF=×28=14,
∴(EX+EQ+RH+HS+TG+GU+FV+WF)+(XW+UV+ST+QR)=14+12=26,
∴EF+FG+HG+EH=26,即长方形EFGH的周长为26,
故选:C.
.【解答】解:由图和已知可知:AB=a,EF=b,AC=n﹣b,GE=n﹣a.
阴影部分的周长为:2(AB+AC)+2(GE+EF)
=2(a+n﹣b)+2(n﹣a+b)
=2a+2n﹣2b+2n﹣2a+2b
=4n.
∴求图中阴影部分的周长之和,只需知道n一个量即可.
故选:D.
.【解答】解:①∵MA=MB,m=2,
∴2﹣a=b﹣2,即b=4﹣a,故此说法正确;
②由①得,当m=5时,b=10﹣a,
∵5<b≤8,
∴5<10﹣a≤8,
解得2≤a<5,
∵a为奇数,
∴a=3,故此说法错误;
③当b=8时,BM=8﹣m,OM=|m|,
∴8﹣m=3|m|,
解得m=2或﹣4,故此说法错误;
④由题意得,b=4,b1=7,b2=10,…,bn=4+3n,
∴MB2022=4+3×2022﹣3=6067,
∴与B2022对应的点A2022表示的数为3﹣6067=﹣6064,故此说法正确.
综上,正确的有①④,
故选:B.
二.填空题
.【解答】解:由W=ma+mb+mc,得W=m(a+b+c),
∴W=2.5×(19.7+32.5+35.8)
=2.5×88
=220.
.【解答】解:x4+ax3+3x2+5x3﹣7x2﹣bx2+6x﹣2=x4+(a+5)x3+(3﹣7﹣b)x2+6x﹣2,
由x4+ax3+3x2+5x3﹣7x2﹣bx2+6x﹣2,合并同类项后不含x3和x2项,得
a+5=0,3﹣7﹣b=0.
解得a=﹣5,b=﹣4.
∴2a+3b=2×(﹣5)+3×(﹣4)=﹣22.
故答案为:﹣22.
.【解答】解:f(10)=,
∵f(0)=0,f(1)=,f(2)=,f()=,f(3)=,f()=,…
∴f(2)+f()=1,f(3)+f()=1,…
∴f(x)+f()=1,
∴f()+f()+…+f()+f(1)+f(0)+f(1)+f(2)+f(19)+f(20)
=f(0)+[f(1)+f(1)]+[f(2)+f()]+…+[f(20)+f()]
=0+1+1+…+1
=20.
故答案为:,20.
.【解答】解:∵S2﹣S1=π(R+3)2﹣πR2,
=6πR+9π,
∴它的面积增加(6πR+9π)cm2.
故答案为:6πR+9π
.【解答】解:设A、B、C原来人数为a人,
根据题意得:a+2+3﹣(a﹣2)
=a+2+3﹣a+2
=7(人),
则最终B组人数为7人.
故答案为:7.
三.解答题
.【解答】解:(1)根据题意得:N=[3x2﹣4x+2﹣(﹣x2+4x﹣4)]=2x2﹣4x+3;
(2)2M﹣N=2(3x2﹣4x+2)﹣(2x2﹣4x+3)=6x2﹣8+4﹣2x2+4x﹣3=4x2﹣4x+1=(2x﹣1)2,
∵(2x﹣1)2≥0.
∴2M﹣N的化简结果不能为负数.
.【解答】解:(1)∵A=2x2+3xy﹣2x﹣1,B=﹣x2+xy+x,
∴3A+6B
=3(2x2+3xy﹣2x﹣1)+6(﹣x2+xy+x)
=6x2+9xy﹣6x﹣3﹣6x2+6xy+6x
=15xy﹣3;
(2)当x=﹣2,y=1时,
15xy﹣3=15×(﹣2)×1﹣3=﹣30﹣3=﹣33.
.【解答】解:(1)整改后A园区的长为:x+y+11x﹣y=12x(米),
宽为:x﹣y﹣(x﹣2y)=y(米),
故答案为:12x米,y米;
(2)依题意有:
,
解得.
.【解答】解(1)(4a﹣b)(4a+b)﹣2(a+b)×2(a+b)
=16a2﹣b2﹣4(a2+2ab+b2)
=16a2﹣b2﹣4a2﹣8ab﹣4b2
=12a2﹣5b2﹣8ab(人).
答:初中部比小学部多(12a2﹣5b2﹣8ab)人.
(2)当a=10,b=2时,
12a2﹣5b2﹣8ab
=12×102﹣5×22﹣8×10×2
=12×100﹣5×4﹣160
=1200﹣20﹣160
=1020(人)
答:当a=10,b=2时,初中部比小学部多1020人.
.【解答】解:(1)由题意得:阴影A的长为(40﹣4y),宽为(x﹣3y),阴影B的长为4y,宽为[x﹣(40﹣4y)]=x﹣40+4y,
则其周长和为:2(40﹣4y+x﹣3y)+2(4y+x﹣40+4y)=4x+2y;
(2)S阴影A﹣S阴影B=(40﹣4y)(x﹣3y)﹣4y(x﹣40+4y)=40x+40y﹣8xy﹣4y2;
(3)∵阴影A与阴影B的面积差不会随着x的变化而变化,
∴40x+40y﹣8xy﹣4y2中,
=(40﹣8y)x+40y﹣4y2
当40﹣8y=0时,
解得:y=5.
一.选择题
1.按照如图所示的计算程序,若x=2,则输出的结果是( )
A.16 B.26 C.﹣16 D.﹣26
2.某楼盘在今年国庆节期间,为了增加销售业绩,提高销售量,该楼盘在原单价为a元/平方米的基础上降价10%,则降价后的单价为( )元/平方米.
A.(1+10%)a B.(1﹣10%)a C.1+10%a D.10%a
3.甲、乙、丙三家商店对一种定价相同的文具开展促销活动.甲商店一次性降价30%;乙商店连续两次降价15%;丙商店先降价20%后又降价10%.若小雪准备在促销活动中,购买此种文具,则下列说法中,正确的是( )
A.小雪到甲商店购买这种文具更合算
B.小雪到乙商店购买这种文具更合算
C.小雪到丙商店购买这种文具更合算
D.在促销活动中,三家商店的这种文具售价相同,小雪可任选一家购买
4.若(2x﹣1)6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,则a6﹣a5+a4﹣a3+a2﹣a1的值为( )
A.0 B.1 C.728 D.729
5.如图,直线AB、CD相交于点O,“阿基米德曲线”从点O开始生成,如果将该曲线与每条射线的交点依次标记为2,﹣4,6,﹣8,10,﹣12,….那么标记“2022”的点在射线( )上.
A.OA B.OB C.OC D.OD
6.若代数式a2﹣3a的值是4,则a2﹣a﹣5的值是( )
A.﹣2 B.﹣3 C.﹣4 D.﹣5
x … ﹣1 0 1 2 …
kx+b … ﹣1 1 3 5 …
7.代数式kx+b当中,当x取值分别为﹣1,0,1,2时,对应代数式的值如下表:
则﹣2k﹣b的值为( )
A.﹣1 B.2 C.﹣3 D.﹣5
8.如图1所示,在长方形ABCD的内部放置了四个周长均为12的小长方形.现将长方形EFGH放置于大长方形ABCD内,且与四个小长方形有重叠(重叠部分均为长方形),如图2所示.已知AB=10,BC=8,四个重叠部分的周长之和为28,则长方形EFGH的周长为( )
A.20 B.24 C.26 D.28
9.已知有2个完全相同的边长为a、b的小长方形和1个边长为m、n的大长方形,小明把这2个小长方形按如图所示放置在大长方形中,小明经过推理得知,要求出图中阴影部分的周长之和,只需知道a、b、m、n中的一个量即可,则要知道的那个量是( )
A.a B.b C.m D.n
10.在原点为O的数轴上,从左到右依次排列的三个动点A,M,B,满足MA=MB,将点A,M,B表示的数分别记为a,m,b.下列说法正确的个数有( )
①当m=2时,b=4﹣a;
②当m=5时,若a为奇数,且5<b≤8,则a=3或5;
③若b=8,BM=3OM,则m=2;
④当m=3,b=4时,将点B水平右移3个单位至点B1,再将点B1水平右移3个单位至点B2,以此类推,…且满足MAn=MBn,则数轴上与B2022对应的点A2022表示的数为﹣6064.
A.1 B.2 C.3 D.4
二.填空题
.已知W=ma+mb+mc,当a=19.7,b=32.5,c=35.8,m=2.5时,W= .
.已知代数式x4+ax3+3x2+5x3﹣7x2﹣bx2+6x﹣2合并同类项后不含x3,x2项,则2a+3b的值 .
.我们定义:f(x)=,则f(10)= ;
f()+f()+…+f()+f(1)+f(0)+f(1)+f(2)+…+f(19)+f(20)= .
.一个圆的半径是rcm,如果它的半径增加3cm,那么它的面积增加 cm2.
.立信初一年级周二体锻课站队时,有三个人数一样多的小组(假设人数足够多)分别记为A、B、C三个小组,依次完成以下三个步骤:第一步,A组二个人去B组;第二步,C组三个人去B组;第三步,A组还有几个人,B组就去多少人到A组.请你确定,最终B组人数为 人.
三.解答题
.在计算题目:“已知:M=3x2﹣4x+2,N=■,求2M﹣N”时,嘉淇把“2M﹣N”看成“M﹣2N”,得到的计算结果是﹣x2+4x﹣4.
(1)求整式N;
(2)判断2M﹣N的化简结果是否能为负数,并说明理由.
.化简求值
已知A=2x2+3xy﹣2x﹣1,B=﹣x2+xy+x,
(1)化简3A+6B;
(2)当x=﹣2,y=1时,求代数式3A+6B的值.
.钟山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米,现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米.
(1)整改后A园区的长为 ,宽为 ;(用代数式表示)
(2)若整改后A园区的长比宽多350米,且整改后两园区的周长之和为980米,求x、y的值.
.某学校初中部和小学部一起在操场做课间操,初中部排成长方形.每排(4a﹣b)人站成(4a+b)排;小学部排成一个边长2(a+b)的方阵.
(1)初中部比小学部多多少人?(用字母a,b表示)
(2)当a=10,b=2时,请计算出此时初中部比小学部多多少人.
.如图,长为40,宽为x的大长方形被分割为9小块,除阴影A,B两块外,其余7块是形状、大小完全相同的小长方形,其较短一边长为y.
(1)分别用含x,y的代数式表示阴影A,B两块的周长,并计算阴影A,B两块的周长和.
(2)分别用含x,y的代数式表示阴影A,B两块的面积,并计算阴影A,B的面积差.
(3)当y取何值时,阴影A与阴影B的面积差不会随着x的变化而变化,并求出这个值.
参考答案与试题解析
一.选择题
1.【解答】解:当x=2时,10﹣x2=10﹣4=6>0,不合题意;
当x=6时,10﹣x2=10﹣36=﹣26<0,符合题意,
故选:D.
2.【解答】解:由题意得,降价后的单价为(1﹣10%)a,
故选:B.
3.【解答】解:在甲商店买这种文具需要:
1×(1﹣30%)
=1×70%
=0.7,
在乙商店买这种文具需要:
1×(1﹣15%)×(1﹣15%)
=1×85%×85%
=0.7225,
在丙商店买这种文具需要:
1×(1﹣20%)×(1﹣10%)
=1×80%×90%
=0.72,
因为0.7<0.72<0.7225,
所以小雪购买这种文具应该去的商店是甲.
故选:A.
4.【解答】解:把x=0代入,得:(﹣1)6=a0
把x=﹣1代入得:
[2×(﹣1)﹣1]6=a6﹣a5+a4﹣a3+a2﹣a1+a0,
(﹣3)6=a6﹣a5+a4﹣a3+a2﹣a1+1,
∴a6﹣a5+a4﹣a3+a2﹣a1=728,
故选:C.
.【解答】解:观察图形的变化可知:
奇数项:2、6、10、14…4n﹣2(n为正整数);
偶数项:﹣4、﹣8、﹣12、﹣16…﹣4n.
∵2022是奇数项,
∴4n﹣2=2022,
∴n=506.
∵每四条射线为一组,OC为始边,
∴506÷4=126…2.
∴标记为“2022”的点在射线OB上.
故选:B.
.【解答】解:∵代数式a2﹣3a的值为4,
∴a2﹣3a=4,
∴
=(a2﹣3a)﹣5
=
=2﹣5
=﹣3.
故选:B.
.【解答】解:∵x=2时,代数式2k+b=5,
∴﹣2k﹣b=﹣(2k+b)=﹣5.
故选:D.
.【解答】解:如图:
∵AB=10,BC=8,
∴AB+BC+CD+DA=2(AB+BC)=36,
∵长方形ABCD的内部放置了四个周长均为12的小长方形,
∴AN+AO=BM+BL=CK+CJ=DI+PD=×12=6,
∴(AB+BC+CD+DA)﹣(AN+AO)﹣(BM+BL)﹣(CK+CJ)﹣(DI+PD)=36﹣6﹣6﹣6﹣6=12,即MN+LK+IJ+OP=12,
∴XW+UV+ST+QR=12,
∵四个重叠部分的周长之和为28,
∴EX+EQ+RH+HS+TG+GU+FV+WF=×28=14,
∴(EX+EQ+RH+HS+TG+GU+FV+WF)+(XW+UV+ST+QR)=14+12=26,
∴EF+FG+HG+EH=26,即长方形EFGH的周长为26,
故选:C.
.【解答】解:由图和已知可知:AB=a,EF=b,AC=n﹣b,GE=n﹣a.
阴影部分的周长为:2(AB+AC)+2(GE+EF)
=2(a+n﹣b)+2(n﹣a+b)
=2a+2n﹣2b+2n﹣2a+2b
=4n.
∴求图中阴影部分的周长之和,只需知道n一个量即可.
故选:D.
.【解答】解:①∵MA=MB,m=2,
∴2﹣a=b﹣2,即b=4﹣a,故此说法正确;
②由①得,当m=5时,b=10﹣a,
∵5<b≤8,
∴5<10﹣a≤8,
解得2≤a<5,
∵a为奇数,
∴a=3,故此说法错误;
③当b=8时,BM=8﹣m,OM=|m|,
∴8﹣m=3|m|,
解得m=2或﹣4,故此说法错误;
④由题意得,b=4,b1=7,b2=10,…,bn=4+3n,
∴MB2022=4+3×2022﹣3=6067,
∴与B2022对应的点A2022表示的数为3﹣6067=﹣6064,故此说法正确.
综上,正确的有①④,
故选:B.
二.填空题
.【解答】解:由W=ma+mb+mc,得W=m(a+b+c),
∴W=2.5×(19.7+32.5+35.8)
=2.5×88
=220.
.【解答】解:x4+ax3+3x2+5x3﹣7x2﹣bx2+6x﹣2=x4+(a+5)x3+(3﹣7﹣b)x2+6x﹣2,
由x4+ax3+3x2+5x3﹣7x2﹣bx2+6x﹣2,合并同类项后不含x3和x2项,得
a+5=0,3﹣7﹣b=0.
解得a=﹣5,b=﹣4.
∴2a+3b=2×(﹣5)+3×(﹣4)=﹣22.
故答案为:﹣22.
.【解答】解:f(10)=,
∵f(0)=0,f(1)=,f(2)=,f()=,f(3)=,f()=,…
∴f(2)+f()=1,f(3)+f()=1,…
∴f(x)+f()=1,
∴f()+f()+…+f()+f(1)+f(0)+f(1)+f(2)+f(19)+f(20)
=f(0)+[f(1)+f(1)]+[f(2)+f()]+…+[f(20)+f()]
=0+1+1+…+1
=20.
故答案为:,20.
.【解答】解:∵S2﹣S1=π(R+3)2﹣πR2,
=6πR+9π,
∴它的面积增加(6πR+9π)cm2.
故答案为:6πR+9π
.【解答】解:设A、B、C原来人数为a人,
根据题意得:a+2+3﹣(a﹣2)
=a+2+3﹣a+2
=7(人),
则最终B组人数为7人.
故答案为:7.
三.解答题
.【解答】解:(1)根据题意得:N=[3x2﹣4x+2﹣(﹣x2+4x﹣4)]=2x2﹣4x+3;
(2)2M﹣N=2(3x2﹣4x+2)﹣(2x2﹣4x+3)=6x2﹣8+4﹣2x2+4x﹣3=4x2﹣4x+1=(2x﹣1)2,
∵(2x﹣1)2≥0.
∴2M﹣N的化简结果不能为负数.
.【解答】解:(1)∵A=2x2+3xy﹣2x﹣1,B=﹣x2+xy+x,
∴3A+6B
=3(2x2+3xy﹣2x﹣1)+6(﹣x2+xy+x)
=6x2+9xy﹣6x﹣3﹣6x2+6xy+6x
=15xy﹣3;
(2)当x=﹣2,y=1时,
15xy﹣3=15×(﹣2)×1﹣3=﹣30﹣3=﹣33.
.【解答】解:(1)整改后A园区的长为:x+y+11x﹣y=12x(米),
宽为:x﹣y﹣(x﹣2y)=y(米),
故答案为:12x米,y米;
(2)依题意有:
,
解得.
.【解答】解(1)(4a﹣b)(4a+b)﹣2(a+b)×2(a+b)
=16a2﹣b2﹣4(a2+2ab+b2)
=16a2﹣b2﹣4a2﹣8ab﹣4b2
=12a2﹣5b2﹣8ab(人).
答:初中部比小学部多(12a2﹣5b2﹣8ab)人.
(2)当a=10,b=2时,
12a2﹣5b2﹣8ab
=12×102﹣5×22﹣8×10×2
=12×100﹣5×4﹣160
=1200﹣20﹣160
=1020(人)
答:当a=10,b=2时,初中部比小学部多1020人.
.【解答】解:(1)由题意得:阴影A的长为(40﹣4y),宽为(x﹣3y),阴影B的长为4y,宽为[x﹣(40﹣4y)]=x﹣40+4y,
则其周长和为:2(40﹣4y+x﹣3y)+2(4y+x﹣40+4y)=4x+2y;
(2)S阴影A﹣S阴影B=(40﹣4y)(x﹣3y)﹣4y(x﹣40+4y)=40x+40y﹣8xy﹣4y2;
(3)∵阴影A与阴影B的面积差不会随着x的变化而变化,
∴40x+40y﹣8xy﹣4y2中,
=(40﹣8y)x+40y﹣4y2
当40﹣8y=0时,
解得:y=5.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
