2013春人教版五年级数学下册 整理与复习(课件)(共39张PPT)
文档属性
| 名称 | 2013春人教版五年级数学下册 整理与复习(课件)(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 11:19:06 | ||
图片预览






文档简介
(共39张PPT)
2023春 人教数学
五年级下册
整理与复习
人教版数学五年级下册课件
3 长方体和正方体
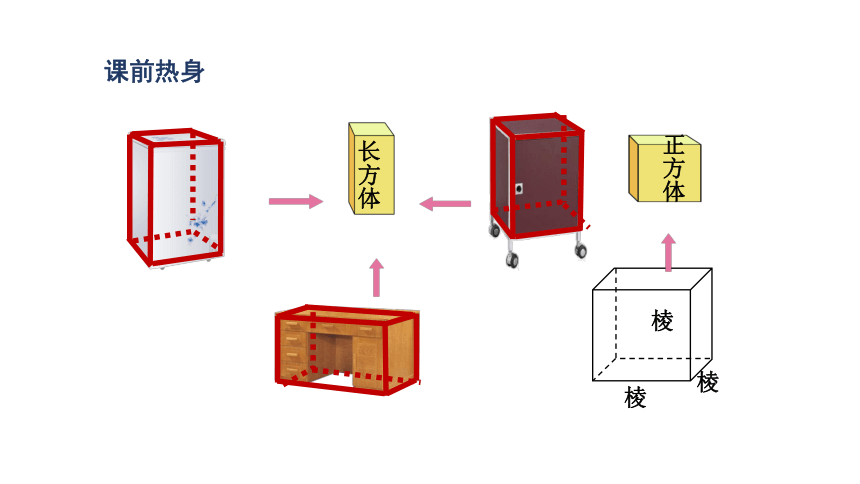
课前热身
长方体
棱
棱
棱
正方体
1、计量一个长方体的棱长用( )单位,计量它的表面积用( )单位,计量它的体积用( )单位。
2、一个正方体的棱长是1厘米,它的表面积是( ),体积是( )。
3、一辆汽车油箱的容积大约是72( )。
长度
面积
体积
6平方厘米
1立方厘米
升
课前热身
4、数学书的体积大约是320( )。
5、一个长方体长3厘米、宽2厘米高1厘米,它的棱长总和是( )。
6、一个长方体纸箱,长和宽都是3分米,高是4分米,做这样的一个纸箱需要纸板( ) 平方分米,它的容积是( ) 立方分米。
立方厘米
24厘米
66
36
课前热身
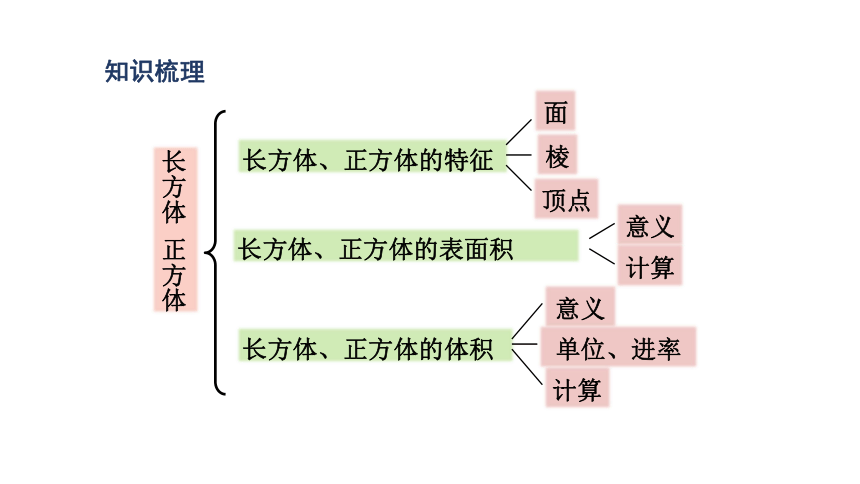
知识梳理
长方体、正方体的特征
长方体、正方体的表面积
长方体、正方体的体积
顶点
面
棱
意义
单位、进率
计算
意义
计算
长方体 正方体
深化知识
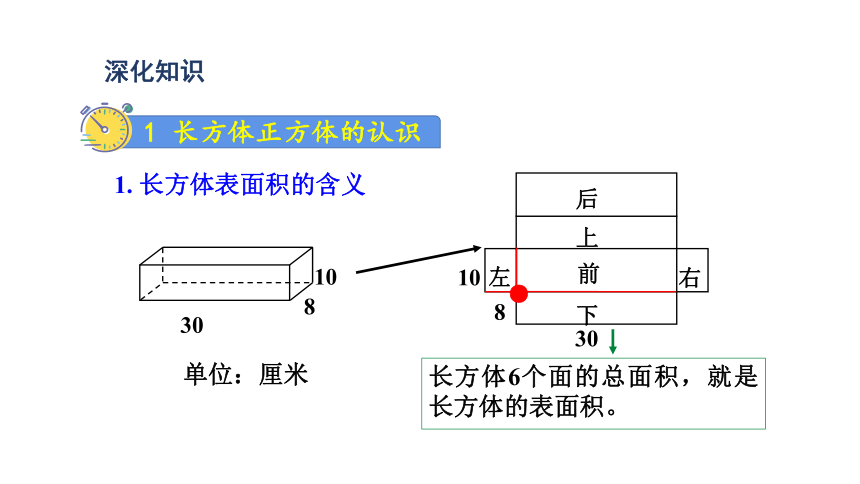
1 长方体正方体的认识
1. 长方体表面积的含义
30
10
8
后
前
上
下
左
右
●
30
10
8
单位:厘米
长方体6个面的总面积,就是长方体的表面积。
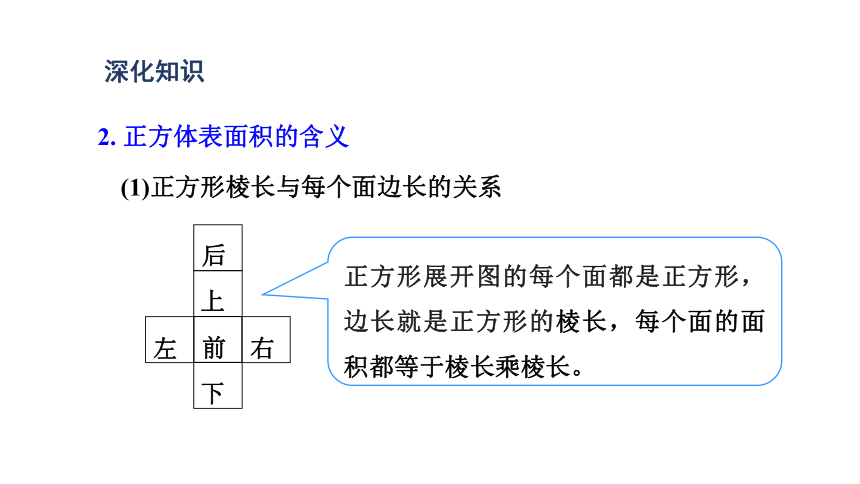
(1)正方形棱长与每个面边长的关系
2. 正方体表面积的含义
前
后
上
下
左
右
正方形展开图的每个面都是正方形,边长就是正方形的棱长,每个面的面积都等于棱长乘棱长。
深化知识
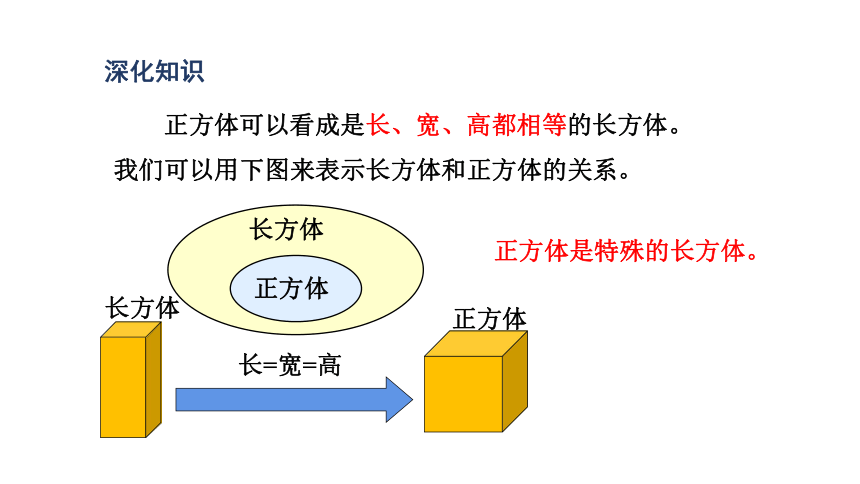
正方体可以看成是长、宽、高都相等的长方体。
我们可以用下图来表示长方体和正方体的关系。
深化知识
长方体
正方体
长方体
正方体是特殊的长方体。
正方体
长=宽=高
深化知识
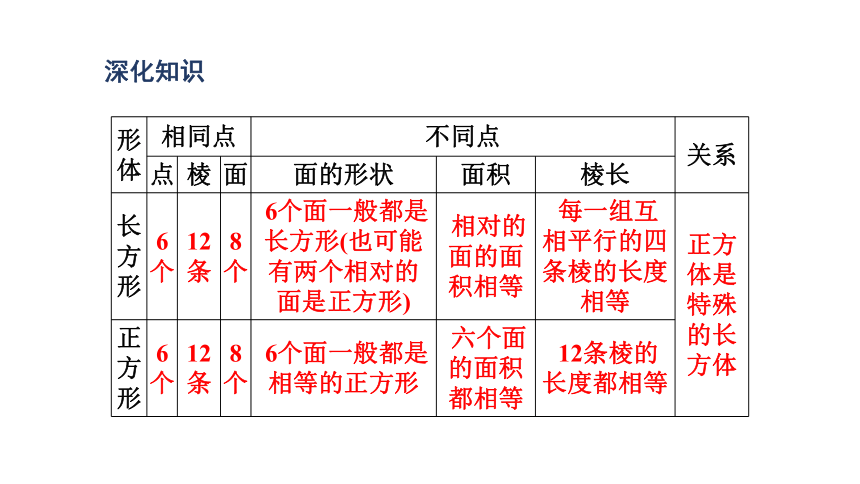
形体 相同点 不同点 关系
点 棱 面 面的形状 面积 棱长 长方形 6个 12条 8个 6个面一般都是长方形(也可能有两个相对的面是正方形) 相对的面的面积相等 每一组互相平行的四条棱的长度相等 正方体是特殊的长方体
正方形 6个 12条 8个 6个面一般都是相等的正方形 六个面的面积都相等 12条棱的长度都相等 对应训练1
1.填空。
(1)长方体有( )个面,相对的面( )。可能这几个面都是长方形,也有可能有( )个面是( )。
(2)长方体有( )个顶点。
(3)长方体有( )条棱,相对的棱长度( )。
6
完全相同
2
正方形
8
12
相等
深化知识
(4)长方体的棱可以分成( )组,每组有( )条。
(5)相交于一个顶点的三条棱的长度分别叫做长方体的( )、( )、( )。
(6)观察一个长方体,最多能看到( )个面。
3
4
长
宽
高
3
深化知识
2. 将正确答案的字母填在括号里。
(1)( )描述的立体图形是正方体。(单位:厘米)
A.三条棱的长是3、3、2
B.三条棱的长是3、2、2
C.三条棱的长是3、3、3
D.长、宽、高都是2
D
深化知识
2. 将正确答案的字母填在括号里。
(2)(易错题)至少用( )个小正方体可以搭成一个较大的正方体。
A.4 B.8
C.12 D.3
B
深化知识
2. 将正确答案的字母填在括号里。
(3)一根长288厘米的铁丝刚好围成一个正方体,则这个正方体的棱长是( )厘米。
A.19 B.24
C.38 D.37
B
深化知识
3.仔细观察,填一填。
(1)上图中长方体的长是( ),宽是( ),高是( )。
(2)前面是( )形,长( ),宽( ),它和( )面是完全相同的。
15cm
12cm
6cm
长方
15cm
6cm
后
深化知识
(3)左面是( )形,长( ),宽( ),它和( )面是完全相同的。
(4)长15 cm,宽12 cm的是( )面和( )面,它们都是( )形。
(5)这个长方体的棱长总和是( )。
长方
12cm
6cm
右
上
下
长方
132cm
深化知识
4.判断。
(1)有两个面是完全一样的正方形的长方体,一定是正方体。 ( )
(2)从正方体的一个顶点引出的三条棱,它们的长度一定相等。 ( )
(3)长方体是特殊的正方体。 ( )
(4)有四个面是完全一样的正方形的长方体,一定是正方体。 ( )
(5)正方体的6个面都是正方形,长方体的6个面都是长方形。 ( )
深化知识
形体 棱长总和 定义 计算公式 常用单位
长方体 长方体或正方体12条棱长的总和 棱长总和=(长+宽+高) ×4 厘米
分米
米
正方体 棱长总和=棱长×12 深化知识
2 长方体和正方体的棱长、表面积、体积、容积和进率
形体 表面积 定义 计算公式 常用单位
长方体 长方体或正方体6个面的总面积 S=(长×宽+长×高+宽×高) ×2 平方厘米
平方分米
平方米
正方体 S=棱长×棱长×6 深化知识
形体 体积(容积) 定义 计算公式 常用单位
长方体 物体所占空间的大小叫做物体的体积。 容器所能容纳物体的体积叫做它们的容积。 V=abh V=Sh 立方厘米
(毫升)
立方分米
(升)
立方米
正方体 V=a V=Sh 深化知识
表面积 体积 容积
意义
计算 方法
长方体或正方体6个面的总面积
物体所占空间的大小
容器所能容纳物体体积的大小
S长=2ab+2ah+2bh
=(ab+ah+bh) ×2
S正=a2×6
V长=abh
V正=a3
V=sh
同体积
(从里面量)
深化知识
表面积 体积 容积
常用计量单位
单位间进率
m dm cm
m dm cm
m dm cm
L ml
1m =100dm
1dm =100cm
1m =1000dm
1dm =1000cm
深化知识
对应训练2
辨析:同一长(正)方体,按不同方式展开得到的平面图是不一样的。
①
②
③
④
⑤
⑥
1.将“展开图”与“立体图形”连起来。
深化知识
2. 上、下每个面,长_____,宽_____,面积是_______;
前、后每个面,长_____,宽_____,面积是_______;
左、右每个面,长_____,宽_____,面积是_______。
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
0.7m
0.5m
0.4m
这个包装箱的表面积是:
0.35×2+0.28×2+0.2×2
=0.7+0.56+0.4
=1.66(m2)
答:至少要用1.66m2的硬纸板。
深化知识
3. 一个玻璃鱼缸的形状是正方体,棱长3dm。制作这个鱼缸时至少需要玻璃多少平方分米 (上面没有盖。)
3×3×5=45(dm2)
答:制作这个鱼缸时至少需要玻璃45dm2。
深化知识
3.填空。
(1)计量体积要用( ),常用的体积单位有( )、( )和( ),可以分别写成( )、( )、( )。
(2)棱长是1 cm、1 dm和1 m的正方体的体积分别是1( )、1( )和1( )。
体积单位
立方厘米
立方分米
立方米
cm3
dm3
m3
cm3
dm3
m3
深化知识
4.判断。
(1)体积单位比面积单位大,面积单位比长度单位大。 ( )
(2)用8个体积为1 cm3的正方体拼成的立体图形,体积一定是8 cm3。 ( )
深化知识
(3)当气球吹起时,体积增大了。 ( )
(4)体积相等的两个长方体,它们的形状一定相同。 ( )
(5)小凤用一块橡皮泥先捏成一个长方体,然后又改捏成一个正方体,体积变小了。 ( )
深化知识
8×8×8=512(dm3)
答:正方体的体积是512立方分米。
26×3=78(cm3)
答:长方体的体积是512立方厘米。
5.
深化知识
6.填空。
2.32 m3=( )dm3 8570 cm3=( )dm3
7.5 m3=( )dm3 9.6 dm2=( )cm2
530 cm3=( )dm3 43.3 dm3=( )cm3
87.2 cm2=( )dm2
2320
8.57
7500
960
0.53
43300
0.872
深化知识
6.填空。
7.62 m3=( )dm3=( )cm3
2670 dm3=( )m3( )dm3
8.25 m2=( )dm2=( )cm2
5.62 m3=( )m3( )dm3
7620
7620000
2
670
825
82500
5
620
深化知识
7.填空。
(1)箱子、油桶、仓库等所能容纳物体的( ),通常叫做它们的( )。
(2)常用的容积单位是( )和( ),也可以写成( )和( )。
(3)长方体或正方体容器容积的计算方法,跟( )的计算方法相同,但要从容器( )量( )、( )、( )。
体积
容积
升
毫升
L
mL
体积
里面
长
宽
高
深化知识
1.把一个棱长为6 cm的正方体框架改做成一个长9 cm、宽5 cm的长方体框架,这个长方体框架的高是多少?
6×12=72(cm) [72-4×(9+5)]÷4=4(cm)
拓展延伸
2.一个长15 cm,宽12 cm,高8 cm的长方体玻璃器皿,能装在一个长18 cm,宽14 cm,容积为1512 cm3的长方体盒子里吗?为什么?
不能,因为1512÷(18×14)=6(cm)
18 cm>15 cm,14 cm>12 cm,6 cm<8 cm,
所以不能装进去。
拓展延伸
3.小丽将一块棱长为4 cm的正方体橡皮泥捏成了一个底面积是8 cm2的长方体,这个长方体的高是多少厘米?
4×4×4÷8=8(cm)
拓展延伸
4.一个长方体玻璃缸,底面是边长为0.2 m的正方形,放入一块石头后水面升高了0.5 m(石头完全浸入水中,水没有溢出),这块石头的体积是多少?(玻璃缸的厚度忽略不计)
0.2×0.2×0.5=0.02(m3)
拓展延伸
5.一块长方体木块,从下部和上部分别截去2 cm和3 cm的长方体后,变成一个正方体,表面积减少了120 cm2,原来长方体木块的体积是多少立方厘米?
2cm
3cm
120÷4÷(2+3)=6(cm)
6×6×(6+3+2)=396(cm3)
拓展延伸
thank you!
2023春 人教数学
五年级下册
整理与复习
人教版数学五年级下册课件
3 长方体和正方体
课前热身
长方体
棱
棱
棱
正方体
1、计量一个长方体的棱长用( )单位,计量它的表面积用( )单位,计量它的体积用( )单位。
2、一个正方体的棱长是1厘米,它的表面积是( ),体积是( )。
3、一辆汽车油箱的容积大约是72( )。
长度
面积
体积
6平方厘米
1立方厘米
升
课前热身
4、数学书的体积大约是320( )。
5、一个长方体长3厘米、宽2厘米高1厘米,它的棱长总和是( )。
6、一个长方体纸箱,长和宽都是3分米,高是4分米,做这样的一个纸箱需要纸板( ) 平方分米,它的容积是( ) 立方分米。
立方厘米
24厘米
66
36
课前热身
知识梳理
长方体、正方体的特征
长方体、正方体的表面积
长方体、正方体的体积
顶点
面
棱
意义
单位、进率
计算
意义
计算
长方体 正方体
深化知识
1 长方体正方体的认识
1. 长方体表面积的含义
30
10
8
后
前
上
下
左
右
●
30
10
8
单位:厘米
长方体6个面的总面积,就是长方体的表面积。
(1)正方形棱长与每个面边长的关系
2. 正方体表面积的含义
前
后
上
下
左
右
正方形展开图的每个面都是正方形,边长就是正方形的棱长,每个面的面积都等于棱长乘棱长。
深化知识
正方体可以看成是长、宽、高都相等的长方体。
我们可以用下图来表示长方体和正方体的关系。
深化知识
长方体
正方体
长方体
正方体是特殊的长方体。
正方体
长=宽=高
深化知识
形体 相同点 不同点 关系
点 棱 面 面的形状 面积 棱长 长方形 6个 12条 8个 6个面一般都是长方形(也可能有两个相对的面是正方形) 相对的面的面积相等 每一组互相平行的四条棱的长度相等 正方体是特殊的长方体
正方形 6个 12条 8个 6个面一般都是相等的正方形 六个面的面积都相等 12条棱的长度都相等 对应训练1
1.填空。
(1)长方体有( )个面,相对的面( )。可能这几个面都是长方形,也有可能有( )个面是( )。
(2)长方体有( )个顶点。
(3)长方体有( )条棱,相对的棱长度( )。
6
完全相同
2
正方形
8
12
相等
深化知识
(4)长方体的棱可以分成( )组,每组有( )条。
(5)相交于一个顶点的三条棱的长度分别叫做长方体的( )、( )、( )。
(6)观察一个长方体,最多能看到( )个面。
3
4
长
宽
高
3
深化知识
2. 将正确答案的字母填在括号里。
(1)( )描述的立体图形是正方体。(单位:厘米)
A.三条棱的长是3、3、2
B.三条棱的长是3、2、2
C.三条棱的长是3、3、3
D.长、宽、高都是2
D
深化知识
2. 将正确答案的字母填在括号里。
(2)(易错题)至少用( )个小正方体可以搭成一个较大的正方体。
A.4 B.8
C.12 D.3
B
深化知识
2. 将正确答案的字母填在括号里。
(3)一根长288厘米的铁丝刚好围成一个正方体,则这个正方体的棱长是( )厘米。
A.19 B.24
C.38 D.37
B
深化知识
3.仔细观察,填一填。
(1)上图中长方体的长是( ),宽是( ),高是( )。
(2)前面是( )形,长( ),宽( ),它和( )面是完全相同的。
15cm
12cm
6cm
长方
15cm
6cm
后
深化知识
(3)左面是( )形,长( ),宽( ),它和( )面是完全相同的。
(4)长15 cm,宽12 cm的是( )面和( )面,它们都是( )形。
(5)这个长方体的棱长总和是( )。
长方
12cm
6cm
右
上
下
长方
132cm
深化知识
4.判断。
(1)有两个面是完全一样的正方形的长方体,一定是正方体。 ( )
(2)从正方体的一个顶点引出的三条棱,它们的长度一定相等。 ( )
(3)长方体是特殊的正方体。 ( )
(4)有四个面是完全一样的正方形的长方体,一定是正方体。 ( )
(5)正方体的6个面都是正方形,长方体的6个面都是长方形。 ( )
深化知识
形体 棱长总和 定义 计算公式 常用单位
长方体 长方体或正方体12条棱长的总和 棱长总和=(长+宽+高) ×4 厘米
分米
米
正方体 棱长总和=棱长×12 深化知识
2 长方体和正方体的棱长、表面积、体积、容积和进率
形体 表面积 定义 计算公式 常用单位
长方体 长方体或正方体6个面的总面积 S=(长×宽+长×高+宽×高) ×2 平方厘米
平方分米
平方米
正方体 S=棱长×棱长×6 深化知识
形体 体积(容积) 定义 计算公式 常用单位
长方体 物体所占空间的大小叫做物体的体积。 容器所能容纳物体的体积叫做它们的容积。 V=abh V=Sh 立方厘米
(毫升)
立方分米
(升)
立方米
正方体 V=a V=Sh 深化知识
表面积 体积 容积
意义
计算 方法
长方体或正方体6个面的总面积
物体所占空间的大小
容器所能容纳物体体积的大小
S长=2ab+2ah+2bh
=(ab+ah+bh) ×2
S正=a2×6
V长=abh
V正=a3
V=sh
同体积
(从里面量)
深化知识
表面积 体积 容积
常用计量单位
单位间进率
m dm cm
m dm cm
m dm cm
L ml
1m =100dm
1dm =100cm
1m =1000dm
1dm =1000cm
深化知识
对应训练2
辨析:同一长(正)方体,按不同方式展开得到的平面图是不一样的。
①
②
③
④
⑤
⑥
1.将“展开图”与“立体图形”连起来。
深化知识
2. 上、下每个面,长_____,宽_____,面积是_______;
前、后每个面,长_____,宽_____,面积是_______;
左、右每个面,长_____,宽_____,面积是_______。
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
0.7m
0.5m
0.4m
这个包装箱的表面积是:
0.35×2+0.28×2+0.2×2
=0.7+0.56+0.4
=1.66(m2)
答:至少要用1.66m2的硬纸板。
深化知识
3. 一个玻璃鱼缸的形状是正方体,棱长3dm。制作这个鱼缸时至少需要玻璃多少平方分米 (上面没有盖。)
3×3×5=45(dm2)
答:制作这个鱼缸时至少需要玻璃45dm2。
深化知识
3.填空。
(1)计量体积要用( ),常用的体积单位有( )、( )和( ),可以分别写成( )、( )、( )。
(2)棱长是1 cm、1 dm和1 m的正方体的体积分别是1( )、1( )和1( )。
体积单位
立方厘米
立方分米
立方米
cm3
dm3
m3
cm3
dm3
m3
深化知识
4.判断。
(1)体积单位比面积单位大,面积单位比长度单位大。 ( )
(2)用8个体积为1 cm3的正方体拼成的立体图形,体积一定是8 cm3。 ( )
深化知识
(3)当气球吹起时,体积增大了。 ( )
(4)体积相等的两个长方体,它们的形状一定相同。 ( )
(5)小凤用一块橡皮泥先捏成一个长方体,然后又改捏成一个正方体,体积变小了。 ( )
深化知识
8×8×8=512(dm3)
答:正方体的体积是512立方分米。
26×3=78(cm3)
答:长方体的体积是512立方厘米。
5.
深化知识
6.填空。
2.32 m3=( )dm3 8570 cm3=( )dm3
7.5 m3=( )dm3 9.6 dm2=( )cm2
530 cm3=( )dm3 43.3 dm3=( )cm3
87.2 cm2=( )dm2
2320
8.57
7500
960
0.53
43300
0.872
深化知识
6.填空。
7.62 m3=( )dm3=( )cm3
2670 dm3=( )m3( )dm3
8.25 m2=( )dm2=( )cm2
5.62 m3=( )m3( )dm3
7620
7620000
2
670
825
82500
5
620
深化知识
7.填空。
(1)箱子、油桶、仓库等所能容纳物体的( ),通常叫做它们的( )。
(2)常用的容积单位是( )和( ),也可以写成( )和( )。
(3)长方体或正方体容器容积的计算方法,跟( )的计算方法相同,但要从容器( )量( )、( )、( )。
体积
容积
升
毫升
L
mL
体积
里面
长
宽
高
深化知识
1.把一个棱长为6 cm的正方体框架改做成一个长9 cm、宽5 cm的长方体框架,这个长方体框架的高是多少?
6×12=72(cm) [72-4×(9+5)]÷4=4(cm)
拓展延伸
2.一个长15 cm,宽12 cm,高8 cm的长方体玻璃器皿,能装在一个长18 cm,宽14 cm,容积为1512 cm3的长方体盒子里吗?为什么?
不能,因为1512÷(18×14)=6(cm)
18 cm>15 cm,14 cm>12 cm,6 cm<8 cm,
所以不能装进去。
拓展延伸
3.小丽将一块棱长为4 cm的正方体橡皮泥捏成了一个底面积是8 cm2的长方体,这个长方体的高是多少厘米?
4×4×4÷8=8(cm)
拓展延伸
4.一个长方体玻璃缸,底面是边长为0.2 m的正方形,放入一块石头后水面升高了0.5 m(石头完全浸入水中,水没有溢出),这块石头的体积是多少?(玻璃缸的厚度忽略不计)
0.2×0.2×0.5=0.02(m3)
拓展延伸
5.一块长方体木块,从下部和上部分别截去2 cm和3 cm的长方体后,变成一个正方体,表面积减少了120 cm2,原来长方体木块的体积是多少立方厘米?
2cm
3cm
120÷4÷(2+3)=6(cm)
6×6×(6+3+2)=396(cm3)
拓展延伸
thank you!
