2023春人教版五年级数学下册整理与复习(课件)(共57张PPT)
文档属性
| 名称 | 2023春人教版五年级数学下册整理与复习(课件)(共57张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 16:41:10 | ||
图片预览







文档简介
(共57张PPT)
2023春 人教数学
五年级下册
整理与复习
人教版数学五年级下册课件
4 分数的意义和性质
( )
1、用分数表示下面各图中的涂色部分
9
4
8
4
2
1
课前热身
5
1
4
1
1、用分数表示下面各图中的涂色部分
课前热身
……
1
7
5
7
2
7
4
7
3
7
6
7
7
7
2、分数单位是 的分数你能写几个?
1
7
课前热身
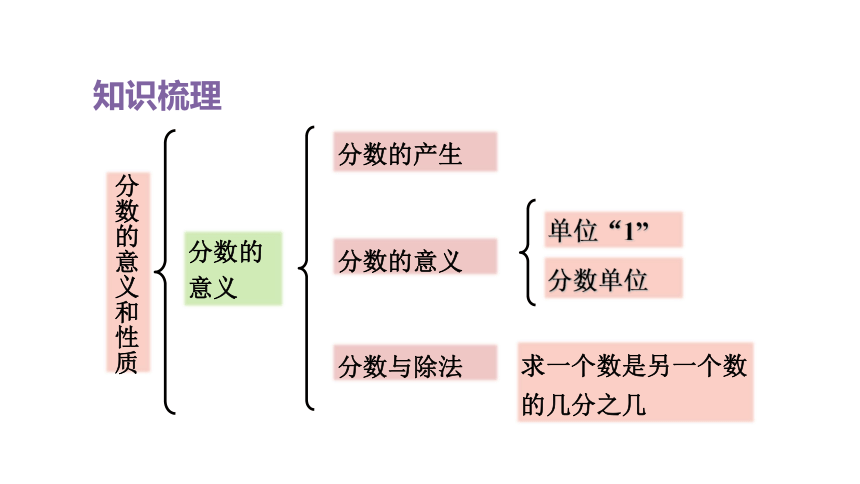
知识梳理
分数的意义和性质
分数的意义
分数的意义
分数的产生
分数与除法
单位“1”
分数单位
求一个数是另一个数的几分之几
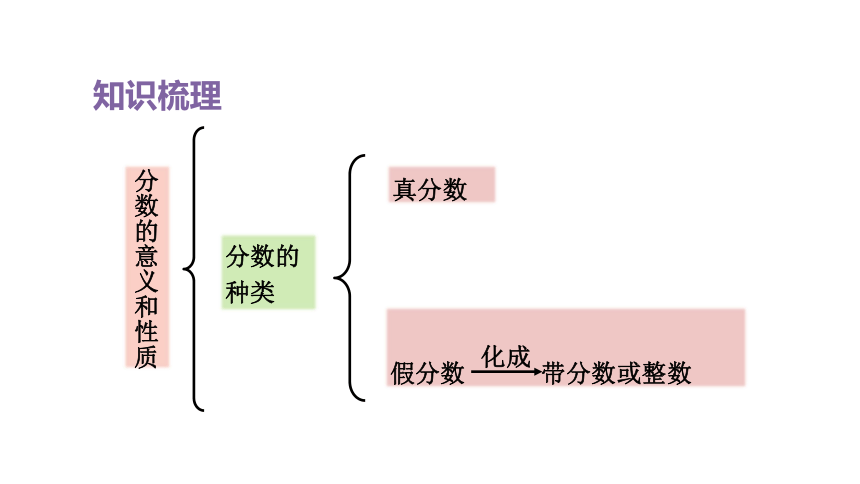
知识梳理
分数的意义和性质
分数的种类
真分数
假分数 带分数或整数
化成
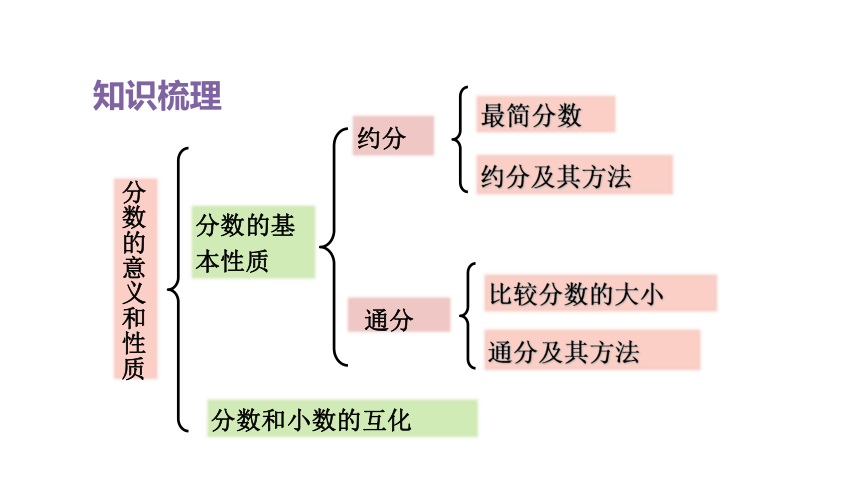
知识梳理
分数的意义和性质
通分
分数的基本性质
约分
最简分数
约分及其方法
分数和小数的互化
比较分数的大小
通分及其方法
1.分数的意义: 把单位“1”平均分成若干份,表这样的一份或者几份的数,叫做分数。表示其中的一份的数,叫做分数单位。若干份是分母,其中的一份或者几份的数是子分。
深化知识
1 分数的意义和性质
一个整体或单位“1”
表示 把单位“1”平均分成5份,取了其中
的三份,叫五分之三。
深化知识
深化知识
对应训练2
求一个数是另一个数的的几分之几可以用除法计算。
比较量÷(单位“1”)的量= 分率
1. 动物园里有大象9头,金丝猴4只。金丝猴的数量是大象的几分之几?
一个数÷另一个数= 分率
4÷9=
答:金丝猴的数量是大象的 。
2. 填一填:
(1)把4m长的绳子平均剪成5段,每段长( )m,每段绳子是全长的( )。
4
5
1
5
深化知识
(2)1985年,第二次大熊猫调查结果显示,全国共有1114只野生大熊猫。2000年开始的第三次大熊猫调查,最终确认我国共有1596只野生大熊猫,其中1206只生活在四川。第二次调查的野生大熊猫的数量是第三次调查数量的( ),生活在四川的野生大熊猫占第三次调查的野生大熊猫数量的( )。
201
266
557
798
深化知识
小结:单位“1”与分数单位的区别
单位“1”表示:一个物体、一些物体、一个计量单位或者一个整体。
分数单位表示:把单位“1”平均分成若干份,其中1份的数。
深化知识
1
3
1÷3=
3
4
3÷4=
被除数相当于分数的分子,除数相当于分数的分母。
被除数÷除数=
被除数
除数
3÷5=
3
5
深化知识
2 分数与除法的关系
如果用字母a表示被除数,b表示除数。
用字母表示分数与除法的关系:
a÷b=
a
b
b可以是0吗?
(b≠ 0)
深化知识
小结:
联 系 区 别
分数
除法
分数是一种数
除法是一种运算
分子
被除数
分数线
除号
分母
(不能为0)
除数
(不能为0)
分数值
商
2、能用分数表示除法算式的商吗?
深化知识
对应训练2
1、在下面的括号里填上适当的数。
7÷13= =( )÷( )
8
5
( )
( )
4
7
7
13
5
8
( )÷7=
4
深化知识
2、这棵纺锤树最粗部分的直径为5 m,一张课桌的长度时它最粗直径的几分之几?
1÷5=
答:一张课桌的长度是它最粗直径的 。
深化知识
巧用对比理解求“一个数是另一个数的几分之几” 的解题方法:如果用字母a(a≠0)表示甲数(较大数),字母b (b≠0)表示乙数(较小数)。则有:
(1)甲数是乙数的多少倍? 用字母表示是:
a÷b。
(2)乙数是甲数的几分之几?用字母表示是:
b÷a。
深化知识
真分数有:
1
3
1
6
假分数有:
3
3
5
3
6
6
7
6
13
6
下面的分数哪些是真分数,哪些是假分数?
1
3
5
3
3
3
6
6
1
6
7
6
13
6
深化知识
3 真分数假分数
分子比分母小的分数叫做真分数。真分数小于1。
分子比分母大或分子和分母相等的分数叫做假分数。假分数大于1或等于1。
你能把假分数化成整数或带分数吗?
3
3
=
1
1
5
3
=
2
3
6
6
=
1
1
7
6
=
1
6
1
=
1
6
13
6
=
真分数有:
1
3
1
6
假分数有:
3
3
5
3
6
6
7
6
13
6
深化知识
小结:真分数、假分数和带分数与1的关系
真分数小于1;
假分数大于1或者等于1;
带分数大于1;
深化知识
对应训练3
1、把这些分数用直线上的点表示出来。
0
1
2
1
3
3
3
5
3
1
6
7
6
13
6
6
6
1
3
3
3
5
3
1
6
6
6
7
6
13
6
深化知识
真
分
数
假
分
数
假
分
数
真
分
数
假
分
数
真
分
数
带
分
数
把上面的假分数化成带分数或整数
深化知识
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。把一个分数化成和它相等,但分子和分母都比较小的分数,叫约分。
一般用分数的分子和分母同时除以它们的公因数(1除外),通常要除到得出最简分数为止。
深化知识
4 分数的基本性质
1、相邻的两个自然数互质(0除外)如:8和9。
3、两个不相同的质数互质。如:23和29。
4、小的数是质数,大的数不是它的倍数的两个数互质。如:11和25.
2、相邻的两个奇数互质。如:13和15.
5、大的数是质数的两个数互质。如:8和31.
7、2和任何奇数互质。
6、1和任何一个自然数(0除外)互质。
互质数的几种特殊情况
深化知识
深化知识
对应训练3
3
13
4
13
<
2、比较下列分数的大小,并说出你的理由。
3
8
3
11
>
2
7
4
7
5
6
5
8
5
9
2
9
12
17
12
19
<
>
>
>
7
7
13
13
9
9
3
3
5
5
12
12
分母相同
分子相同
的两个分数,分子大的分数就大。
的两个分数,分母小的分数就大。
大家说一说:分母相同的两个分数怎样比较大小?分子相同的两个分数呢
深化知识
3
4
5
6
<
可以先通分,把它们化成分母相同的分数。
6
5
=
6×2
5×2
=
10
12
=
4
3
=
4×3
3×3
=
9
12
=
因为
9
12
<
10
12
,所以
3
4
<
5
6
大家说一说:分子和分母都不相同的两个分数怎么比较大小
1. 8和12的最大公因数是几呢?
2. 用自己的话说一说什么是公因数和最大公因数。
8的因数
12的因数
8
4
2,
3,6,
12
1,
8和12的公因数
4
公因数是两个数的因数中相同的因数;
最大公因数就是公因数中最大的那个数。
深化知识
5 最大公因数和最小公倍数
12,24,36,··· 是 4 和 6 公有的倍数,叫做它们的公倍数。其中, 12 是最小的公倍数,叫做它们的最小公倍数。
4 的倍数
6 的倍数
4,8,16,20,28,32,40,
···
6,18,
30,42,…
12,24,
36,···
想一想,两个数有没有最大公倍数?
还可以这样表示。
深化知识
对应训练5
4
12
1
1
1
1.找出下列每组数的最大公因数。
4和8 12和36 1和7 8和9 12和35
深化知识
对应训练5
2、找出下列每组数的最小公倍数。你发现了什么
3 和 6
2 和 8
5 和 6
4 和 9
3 和 6 的最小公倍数是 6;
2 和 8 的最小公倍数是 8 ;
5 和 6 的最小公倍数是 30 ;
4 和 9 的最小公倍数是 36。
深化知识
如果两个数互质,最小公倍数是它们的乘积;
如果两个数是倍数关系,较大数是它们的最小公倍数。
总结:
你能举例验证吗?
深化知识
分解质因数的方法也用于约分
必须看准分子分母。
1、分子分母都是偶数除以2。
2、分子分母同时是0或5除以5.
3、分子分母都是奇数或一奇一偶找3、7和11.
4、除此之外看大数是否是小数的倍数。
5、当分子分母中小的数是质数时,一定要看大数是否是小数的倍数,如果是就要同时除以小的数。
深化知识
6 约分
对应训练6
1. 把上下两行相等的两个分数用线连起来。
深化知识
一、 把异分母分数化成和原来分数相等的同分母分数,叫做通分。用乘法。
1.异分母化成同分母;
2.分数大小不变。
深化知识
7 通分
二、通分的一般方法:
1、求原来几个分母的最小公倍数。
2、把各分数化成以这个最小公倍数作分母的分数。
深化知识
对应训练7
1.比较下面每组中的两个分数的大小。
<
>
>
<
2. 里面有( )个 , 是( )个 ,所以 。
7
5
>
深化知识
0.125
3
10
0.5
1
4
0
1
0.25
0.3
0.8
1
8
1
2
5
8
3
4
0.75
4
5
在 里填上适当的小数或分数。
0.625
深化知识
8 分数与小数互化
用小数表示
用分数表示
40cm
150g
125cm2
3680dm3
m
m
kg
kg
dm2
dm2
m3
m3
0.4
0.15
1.25
3.68
2
5
1
4
1
3
20
17
25
3
深化知识
分母不是10、100、1000……的分数化小数,可以用分子除以分母;除不尽的,可以根据需要按四舍五入法保留几位小数。
分母是10,100,1000,……的分数化小数,可以直接去掉分母,看分母中1后面有几个0,就在分子中从最后一位起向左数出几位,点上小数点。
分数化小数的方法:
深化知识
除得尽的分数,分母分解质因数只有2或5。除了2或5还有别的质因数一定除不尽。
深化知识
对应训练8
用分子除以分母除不尽时,要根据需要按
“四舍五入”法保留几位小数。
=0.7 =3÷4=0.75 =2÷9≈0.22
10
7
4
3
9
2
=0.39 =9÷40=0.225 =5÷14≈0.36
100
39
40
9
14
5
深化知识
提示:
分母是10、100的分数化成小数,可以先去
掉分母,再在分子中从最后一位起分别向
左数出一位、两位,点上小数点。
深化知识
2.填空。
(1)0.5里面有( )个( )分之一,表示( )分之( ),化成分数是( )。
(2)0.35里面有( )个( )分之一,表示( )分之( ),化成分数是( )。
(3)0.006里面有( )个( )分之一,表示( )分之( ),化成分数是( )。
5
十
十
五
35
百
百
三十五
6
千
千
六
深化知识
1.
25分钟= 小时;
小时等于 小时
答:小林家离学校远些。
如果他们两人的行走速度相同,谁家离学校远些?
拓展延伸
48的因数:
1,
48
2,
24,
3,
16,
4,
12,
6,
8,
答:每组最多6人。
48和54的最大公因数是 6。
2、
拓展延伸
3.金湖县城公交车调度站早上5时40分同时发1路车和2路车,1路车每隔10分钟发一辆,2路车每隔12分钟发一辆,这两路车几时几分第二次同时发车?(先填表再回答)
10=5×2
12=3×2×2
5×3×2×2=60(分)
5时40分+60分=6时40分
答:这两路车6时40分第二次同时发车。
辨析:灵活运用所学知识推理
拓展延伸
4.一种瓷砖长4 dm,宽3 dm,如果用这种瓷砖铺成一个正方形的地面(用的瓷砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
4×3=12(dm)
答:正方形的边长最小是12 dm,正方形的边长可以是
12 dm,24 dm,36 dm,48 dm,…。
拓展延伸
5.五(1)班男生有27人,女生有18人,男女生分别分组做游戏,要使每组人数相同,每组最多有多少人?可以分成几组?
每组最多有:3×3=9(人)
可以分成27÷9+18÷9=5(组)
答:每组最多有9人可以分成5组。
3
3
3
27
9
18
6
2
拓展延伸
6.幼儿园买回49个苹果和29个梨。老师把两种水果平均分给中班的每个小朋友,结果苹果多4个,梨少1个。中班最多有多少个小朋友?
49-4=45(个) 29+1=30(个)
3×5=15(个)
答:中班最多有15个小朋友。
辨析:求最多有多少名同学,就是求相关数的最大公因数
3
5
3
45
15
30
10
2
拓展延伸
7.动物园是10路和15路公交车的起点站,10路车每8分钟发一次车,15路车每10分钟发一次车。这两路公交车在早上6时同时发车后,至少再过多少分钟又同时发车?这时是几时几分?
8和10的最小公倍数是40,至少再过40分钟又同时发车,这时是6时40分。
拓展延伸
8、某班级有学生若干人,若6人一排,则少3人,若7人一排,则多3人,这个班至少有多少人?
6人一排,则少3人,也可看成多3人,6×7+3=45(人)。
拓展延伸
9.把一张长60 cm,宽40 cm的长方形铁皮剪成同样大小的正方形铁皮,要使剪成的正方形最大且无剩余,正方形的边长应是多少厘米?可以剪几个?
60和40的最大公因数是20
(60÷20)×(40÷20)=6(个)
即正方形的边长应是20 cm,可以剪6个。
拓展延伸
10、一个分数,用2约了2次,用3约了1次,结果是 ,这个分数原来是多少?
拓展延伸
thank you!
2023春 人教数学
五年级下册
整理与复习
人教版数学五年级下册课件
4 分数的意义和性质
( )
1、用分数表示下面各图中的涂色部分
9
4
8
4
2
1
课前热身
5
1
4
1
1、用分数表示下面各图中的涂色部分
课前热身
……
1
7
5
7
2
7
4
7
3
7
6
7
7
7
2、分数单位是 的分数你能写几个?
1
7
课前热身
知识梳理
分数的意义和性质
分数的意义
分数的意义
分数的产生
分数与除法
单位“1”
分数单位
求一个数是另一个数的几分之几
知识梳理
分数的意义和性质
分数的种类
真分数
假分数 带分数或整数
化成
知识梳理
分数的意义和性质
通分
分数的基本性质
约分
最简分数
约分及其方法
分数和小数的互化
比较分数的大小
通分及其方法
1.分数的意义: 把单位“1”平均分成若干份,表这样的一份或者几份的数,叫做分数。表示其中的一份的数,叫做分数单位。若干份是分母,其中的一份或者几份的数是子分。
深化知识
1 分数的意义和性质
一个整体或单位“1”
表示 把单位“1”平均分成5份,取了其中
的三份,叫五分之三。
深化知识
深化知识
对应训练2
求一个数是另一个数的的几分之几可以用除法计算。
比较量÷(单位“1”)的量= 分率
1. 动物园里有大象9头,金丝猴4只。金丝猴的数量是大象的几分之几?
一个数÷另一个数= 分率
4÷9=
答:金丝猴的数量是大象的 。
2. 填一填:
(1)把4m长的绳子平均剪成5段,每段长( )m,每段绳子是全长的( )。
4
5
1
5
深化知识
(2)1985年,第二次大熊猫调查结果显示,全国共有1114只野生大熊猫。2000年开始的第三次大熊猫调查,最终确认我国共有1596只野生大熊猫,其中1206只生活在四川。第二次调查的野生大熊猫的数量是第三次调查数量的( ),生活在四川的野生大熊猫占第三次调查的野生大熊猫数量的( )。
201
266
557
798
深化知识
小结:单位“1”与分数单位的区别
单位“1”表示:一个物体、一些物体、一个计量单位或者一个整体。
分数单位表示:把单位“1”平均分成若干份,其中1份的数。
深化知识
1
3
1÷3=
3
4
3÷4=
被除数相当于分数的分子,除数相当于分数的分母。
被除数÷除数=
被除数
除数
3÷5=
3
5
深化知识
2 分数与除法的关系
如果用字母a表示被除数,b表示除数。
用字母表示分数与除法的关系:
a÷b=
a
b
b可以是0吗?
(b≠ 0)
深化知识
小结:
联 系 区 别
分数
除法
分数是一种数
除法是一种运算
分子
被除数
分数线
除号
分母
(不能为0)
除数
(不能为0)
分数值
商
2、能用分数表示除法算式的商吗?
深化知识
对应训练2
1、在下面的括号里填上适当的数。
7÷13= =( )÷( )
8
5
( )
( )
4
7
7
13
5
8
( )÷7=
4
深化知识
2、这棵纺锤树最粗部分的直径为5 m,一张课桌的长度时它最粗直径的几分之几?
1÷5=
答:一张课桌的长度是它最粗直径的 。
深化知识
巧用对比理解求“一个数是另一个数的几分之几” 的解题方法:如果用字母a(a≠0)表示甲数(较大数),字母b (b≠0)表示乙数(较小数)。则有:
(1)甲数是乙数的多少倍? 用字母表示是:
a÷b。
(2)乙数是甲数的几分之几?用字母表示是:
b÷a。
深化知识
真分数有:
1
3
1
6
假分数有:
3
3
5
3
6
6
7
6
13
6
下面的分数哪些是真分数,哪些是假分数?
1
3
5
3
3
3
6
6
1
6
7
6
13
6
深化知识
3 真分数假分数
分子比分母小的分数叫做真分数。真分数小于1。
分子比分母大或分子和分母相等的分数叫做假分数。假分数大于1或等于1。
你能把假分数化成整数或带分数吗?
3
3
=
1
1
5
3
=
2
3
6
6
=
1
1
7
6
=
1
6
1
=
1
6
13
6
=
真分数有:
1
3
1
6
假分数有:
3
3
5
3
6
6
7
6
13
6
深化知识
小结:真分数、假分数和带分数与1的关系
真分数小于1;
假分数大于1或者等于1;
带分数大于1;
深化知识
对应训练3
1、把这些分数用直线上的点表示出来。
0
1
2
1
3
3
3
5
3
1
6
7
6
13
6
6
6
1
3
3
3
5
3
1
6
6
6
7
6
13
6
深化知识
真
分
数
假
分
数
假
分
数
真
分
数
假
分
数
真
分
数
带
分
数
把上面的假分数化成带分数或整数
深化知识
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。把一个分数化成和它相等,但分子和分母都比较小的分数,叫约分。
一般用分数的分子和分母同时除以它们的公因数(1除外),通常要除到得出最简分数为止。
深化知识
4 分数的基本性质
1、相邻的两个自然数互质(0除外)如:8和9。
3、两个不相同的质数互质。如:23和29。
4、小的数是质数,大的数不是它的倍数的两个数互质。如:11和25.
2、相邻的两个奇数互质。如:13和15.
5、大的数是质数的两个数互质。如:8和31.
7、2和任何奇数互质。
6、1和任何一个自然数(0除外)互质。
互质数的几种特殊情况
深化知识
深化知识
对应训练3
3
13
4
13
<
2、比较下列分数的大小,并说出你的理由。
3
8
3
11
>
2
7
4
7
5
6
5
8
5
9
2
9
12
17
12
19
<
>
>
>
7
7
13
13
9
9
3
3
5
5
12
12
分母相同
分子相同
的两个分数,分子大的分数就大。
的两个分数,分母小的分数就大。
大家说一说:分母相同的两个分数怎样比较大小?分子相同的两个分数呢
深化知识
3
4
5
6
<
可以先通分,把它们化成分母相同的分数。
6
5
=
6×2
5×2
=
10
12
=
4
3
=
4×3
3×3
=
9
12
=
因为
9
12
<
10
12
,所以
3
4
<
5
6
大家说一说:分子和分母都不相同的两个分数怎么比较大小
1. 8和12的最大公因数是几呢?
2. 用自己的话说一说什么是公因数和最大公因数。
8的因数
12的因数
8
4
2,
3,6,
12
1,
8和12的公因数
4
公因数是两个数的因数中相同的因数;
最大公因数就是公因数中最大的那个数。
深化知识
5 最大公因数和最小公倍数
12,24,36,··· 是 4 和 6 公有的倍数,叫做它们的公倍数。其中, 12 是最小的公倍数,叫做它们的最小公倍数。
4 的倍数
6 的倍数
4,8,16,20,28,32,40,
···
6,18,
30,42,…
12,24,
36,···
想一想,两个数有没有最大公倍数?
还可以这样表示。
深化知识
对应训练5
4
12
1
1
1
1.找出下列每组数的最大公因数。
4和8 12和36 1和7 8和9 12和35
深化知识
对应训练5
2、找出下列每组数的最小公倍数。你发现了什么
3 和 6
2 和 8
5 和 6
4 和 9
3 和 6 的最小公倍数是 6;
2 和 8 的最小公倍数是 8 ;
5 和 6 的最小公倍数是 30 ;
4 和 9 的最小公倍数是 36。
深化知识
如果两个数互质,最小公倍数是它们的乘积;
如果两个数是倍数关系,较大数是它们的最小公倍数。
总结:
你能举例验证吗?
深化知识
分解质因数的方法也用于约分
必须看准分子分母。
1、分子分母都是偶数除以2。
2、分子分母同时是0或5除以5.
3、分子分母都是奇数或一奇一偶找3、7和11.
4、除此之外看大数是否是小数的倍数。
5、当分子分母中小的数是质数时,一定要看大数是否是小数的倍数,如果是就要同时除以小的数。
深化知识
6 约分
对应训练6
1. 把上下两行相等的两个分数用线连起来。
深化知识
一、 把异分母分数化成和原来分数相等的同分母分数,叫做通分。用乘法。
1.异分母化成同分母;
2.分数大小不变。
深化知识
7 通分
二、通分的一般方法:
1、求原来几个分母的最小公倍数。
2、把各分数化成以这个最小公倍数作分母的分数。
深化知识
对应训练7
1.比较下面每组中的两个分数的大小。
<
>
>
<
2. 里面有( )个 , 是( )个 ,所以 。
7
5
>
深化知识
0.125
3
10
0.5
1
4
0
1
0.25
0.3
0.8
1
8
1
2
5
8
3
4
0.75
4
5
在 里填上适当的小数或分数。
0.625
深化知识
8 分数与小数互化
用小数表示
用分数表示
40cm
150g
125cm2
3680dm3
m
m
kg
kg
dm2
dm2
m3
m3
0.4
0.15
1.25
3.68
2
5
1
4
1
3
20
17
25
3
深化知识
分母不是10、100、1000……的分数化小数,可以用分子除以分母;除不尽的,可以根据需要按四舍五入法保留几位小数。
分母是10,100,1000,……的分数化小数,可以直接去掉分母,看分母中1后面有几个0,就在分子中从最后一位起向左数出几位,点上小数点。
分数化小数的方法:
深化知识
除得尽的分数,分母分解质因数只有2或5。除了2或5还有别的质因数一定除不尽。
深化知识
对应训练8
用分子除以分母除不尽时,要根据需要按
“四舍五入”法保留几位小数。
=0.7 =3÷4=0.75 =2÷9≈0.22
10
7
4
3
9
2
=0.39 =9÷40=0.225 =5÷14≈0.36
100
39
40
9
14
5
深化知识
提示:
分母是10、100的分数化成小数,可以先去
掉分母,再在分子中从最后一位起分别向
左数出一位、两位,点上小数点。
深化知识
2.填空。
(1)0.5里面有( )个( )分之一,表示( )分之( ),化成分数是( )。
(2)0.35里面有( )个( )分之一,表示( )分之( ),化成分数是( )。
(3)0.006里面有( )个( )分之一,表示( )分之( ),化成分数是( )。
5
十
十
五
35
百
百
三十五
6
千
千
六
深化知识
1.
25分钟= 小时;
小时等于 小时
答:小林家离学校远些。
如果他们两人的行走速度相同,谁家离学校远些?
拓展延伸
48的因数:
1,
48
2,
24,
3,
16,
4,
12,
6,
8,
答:每组最多6人。
48和54的最大公因数是 6。
2、
拓展延伸
3.金湖县城公交车调度站早上5时40分同时发1路车和2路车,1路车每隔10分钟发一辆,2路车每隔12分钟发一辆,这两路车几时几分第二次同时发车?(先填表再回答)
10=5×2
12=3×2×2
5×3×2×2=60(分)
5时40分+60分=6时40分
答:这两路车6时40分第二次同时发车。
辨析:灵活运用所学知识推理
拓展延伸
4.一种瓷砖长4 dm,宽3 dm,如果用这种瓷砖铺成一个正方形的地面(用的瓷砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
4×3=12(dm)
答:正方形的边长最小是12 dm,正方形的边长可以是
12 dm,24 dm,36 dm,48 dm,…。
拓展延伸
5.五(1)班男生有27人,女生有18人,男女生分别分组做游戏,要使每组人数相同,每组最多有多少人?可以分成几组?
每组最多有:3×3=9(人)
可以分成27÷9+18÷9=5(组)
答:每组最多有9人可以分成5组。
3
3
3
27
9
18
6
2
拓展延伸
6.幼儿园买回49个苹果和29个梨。老师把两种水果平均分给中班的每个小朋友,结果苹果多4个,梨少1个。中班最多有多少个小朋友?
49-4=45(个) 29+1=30(个)
3×5=15(个)
答:中班最多有15个小朋友。
辨析:求最多有多少名同学,就是求相关数的最大公因数
3
5
3
45
15
30
10
2
拓展延伸
7.动物园是10路和15路公交车的起点站,10路车每8分钟发一次车,15路车每10分钟发一次车。这两路公交车在早上6时同时发车后,至少再过多少分钟又同时发车?这时是几时几分?
8和10的最小公倍数是40,至少再过40分钟又同时发车,这时是6时40分。
拓展延伸
8、某班级有学生若干人,若6人一排,则少3人,若7人一排,则多3人,这个班至少有多少人?
6人一排,则少3人,也可看成多3人,6×7+3=45(人)。
拓展延伸
9.把一张长60 cm,宽40 cm的长方形铁皮剪成同样大小的正方形铁皮,要使剪成的正方形最大且无剩余,正方形的边长应是多少厘米?可以剪几个?
60和40的最大公因数是20
(60÷20)×(40÷20)=6(个)
即正方形的边长应是20 cm,可以剪6个。
拓展延伸
10、一个分数,用2约了2次,用3约了1次,结果是 ,这个分数原来是多少?
拓展延伸
thank you!
