14.4.3用频率直方图估计总体分布 教案
文档属性
| 名称 | 14.4.3用频率直方图估计总体分布 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 265.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 07:38:40 | ||
图片预览


文档简介
第7课时 用频率直方图估计总体分布
【教学目标】
1.结合实例,能用样本估计总体的取值规律.
2.能根据频率分布表和频率直方图观测数据的分布规律.
【教学过程】
一、问题情境
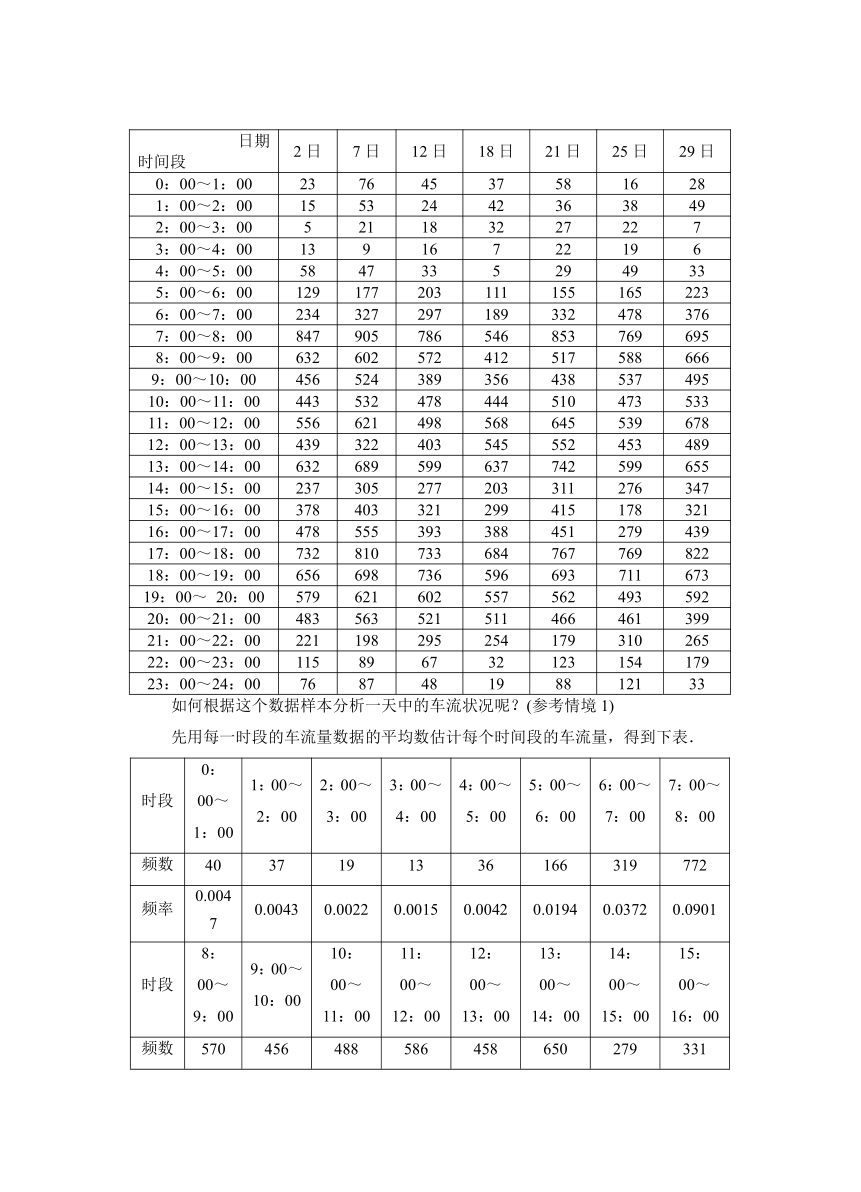
情境1:为了实现绿色发展,避免能源浪费,某市政府计划对居民用电采用阶梯收费的方法.为此,相关部门在该市随机调查了200户居民六月份的用电量(单位:kW·h),以了解这个城市家庭用电的情况.
其频率直方图如图所示:
(根据前几课时的学习)为了设计较为合理的收费方法,需要做哪些工作?
答:抽样调查→分析样本数据→通过样本数据来估计全市居民用水量的分布情况.
上图中蕴含了哪些信息?请根据图表归纳居民月均用电量的分布规律.
(答案不唯一,如[80,160]内的数据较多等)
试查阅相关资料,了解阶梯电价产生的背景,以及居民阶梯电价的电量分档和电价确定等相关信息.
情境2:现在很多城市面临交通拥挤的状况,特别是上下班高峰期时堵车现象时有发生.城市交通管理部门需要根据不同时段的车流量制定相应的管理办法.如何了解一天中车流量的分布状况呢?
二、数学建构
假定根据选定的方案实施后已经得到如下数据:
日期 时间段 2日 7日 12日 18日 21日 25日 29日
0:00~1:00 23 76 45 37 58 16 28
1:00~2:00 15 53 24 42 36 38 49
2:00~3:00 5 21 18 32 27 22 7
3:00~4:00 13 9 16 7 22 19 6
4:00~5:00 58 47 33 5 29 49 33
5:00~6:00 129 177 203 111 155 165 223
6:00~7:00 234 327 297 189 332 478 376
7:00~8:00 847 905 786 546 853 769 695
8:00~9:00 632 602 572 412 517 588 666
9:00~10:00 456 524 389 356 438 537 495
10:00~11:00 443 532 478 444 510 473 533
11:00~12:00 556 621 498 568 645 539 678
12:00~13:00 439 322 403 545 552 453 489
13:00~14:00 632 689 599 637 742 599 655
14:00~15:00 237 305 277 203 311 276 347
15:00~16:00 378 403 321 299 415 178 321
16:00~17:00 478 555 393 388 451 279 439
17:00~18:00 732 810 733 684 767 769 822
18:00~19:00 656 698 736 596 693 711 673
19:00~ 20:00 579 621 602 557 562 493 592
20:00~21:00 483 563 521 511 466 461 399
21:00~22:00 221 198 295 254 179 310 265
22:00~23:00 115 89 67 32 123 154 179
23:00~24:00 76 87 48 19 88 121 33
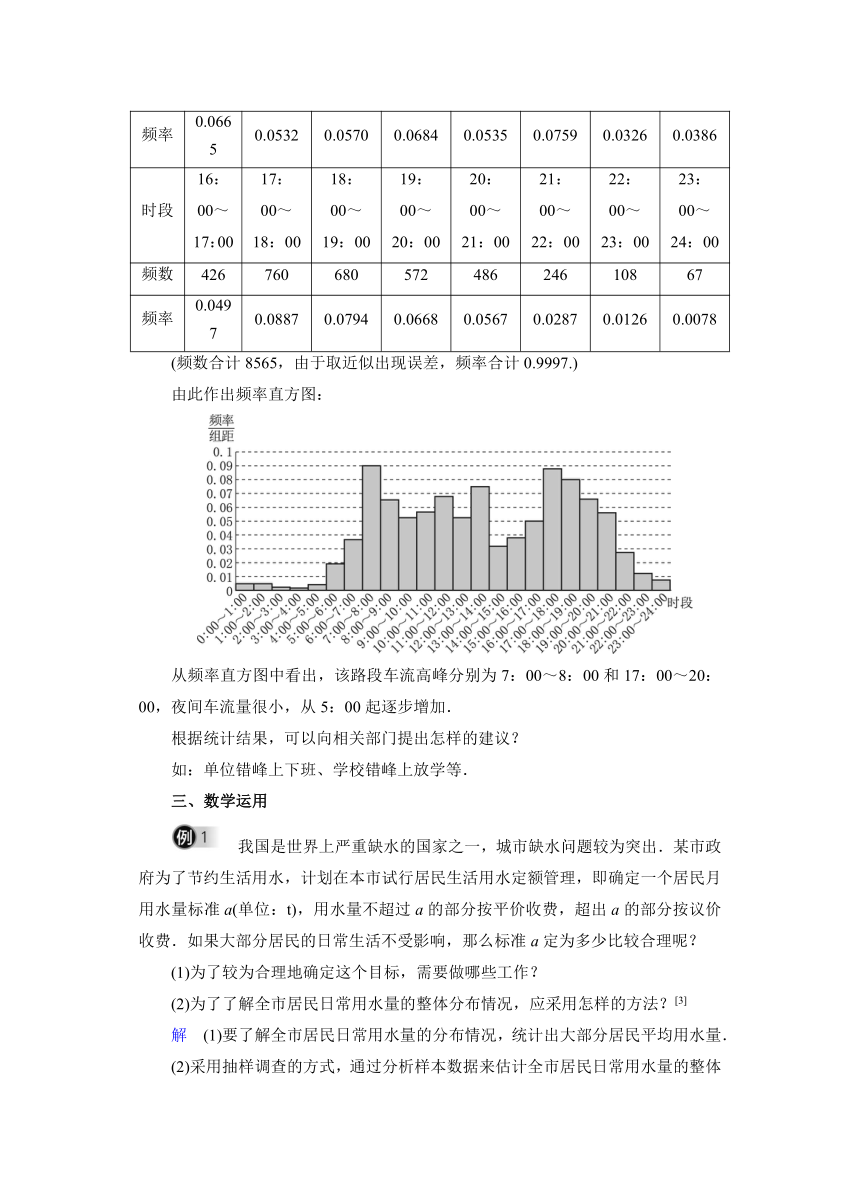
如何根据这个数据样本分析一天中的车流状况呢?(参考情境1)
先用每一时段的车流量数据的平均数估计每个时间段的车流量,得到下表.
时段 0:00~ 1:00 1:00~ 2:00 2:00~ 3:00 3:00~ 4:00 4:00~ 5:00 5:00~ 6:00 6:00~ 7:00 7:00~ 8:00
频数 40 37 19 13 36 166 319 772
频率 0.0047 0.0043 0.0022 0.0015 0.0042 0.0194 0.0372 0.0901
时段 8:00~ 9:00 9:00~ 10:00 10:00~ 11:00 11:00~ 12:00 12:00~ 13:00 13:00~ 14:00 14:00~ 15:00 15:00~ 16:00
频数 570 456 488 586 458 650 279 331
频率 0.0665 0.0532 0.0570 0.0684 0.0535 0.0759 0.0326 0.0386
时段 16:00~ 17:00 17:00~ 18:00 18:00~ 19:00 19:00~ 20:00 20:00~ 21:00 21:00~ 22:00 22:00~ 23:00 23:00~ 24:00
频数 426 760 680 572 486 246 108 67
频率 0.0497 0.0887 0.0794 0.0668 0.0567 0.0287 0.0126 0.0078
(频数合计8565,由于取近似出现误差,频率合计0.9997.)
由此作出频率直方图:
从频率直方图中看出,该路段车流高峰分别为7:00~8:00和17:00~20:00,夜间车流量很小,从5:00起逐步增加.
根据统计结果,可以向相关部门提出怎样的建议?
如:单位错峰上下班、学校错峰上放学等.
三、数学运用
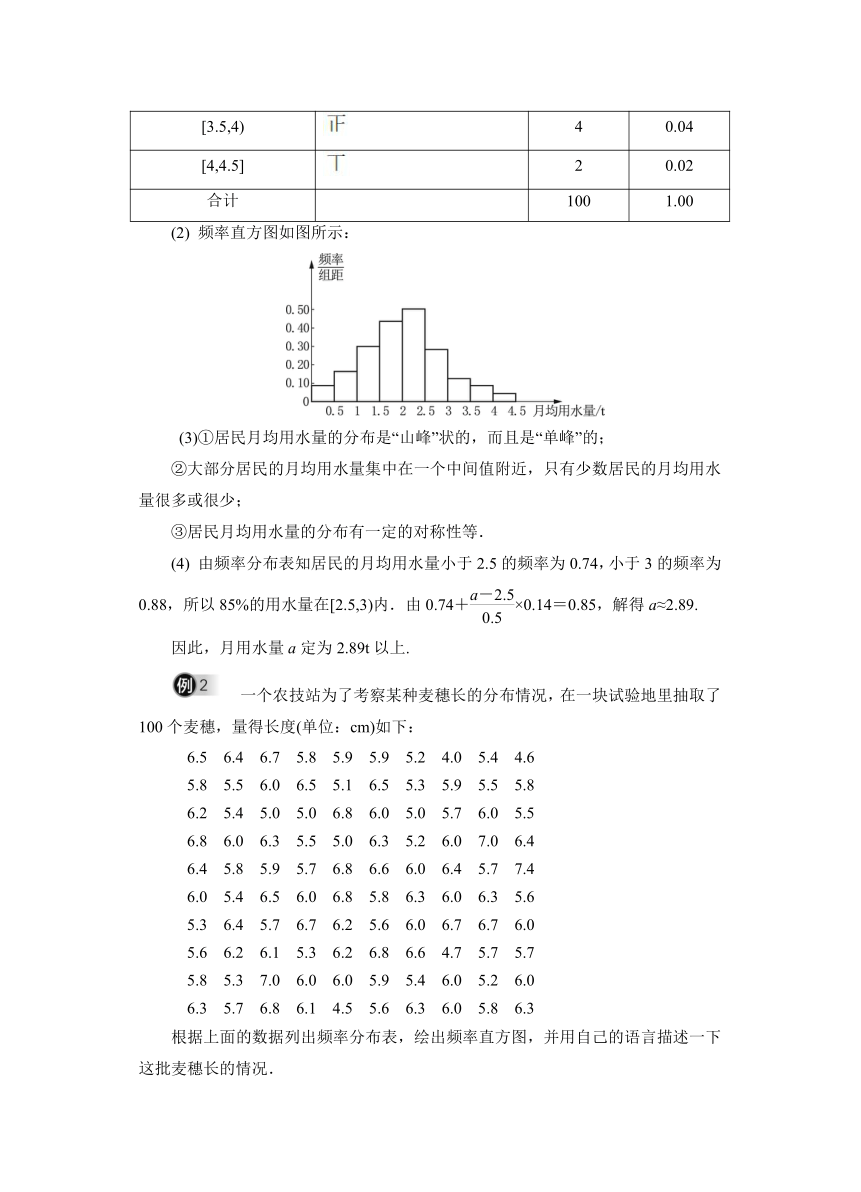
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a(单位:t),用水量不超过a的部分按平价收费,超出a的部分按议价收费.如果大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢?
(1)为了较为合理地确定这个目标,需要做哪些工作?
(2)为了了解全市居民日常用水量的整体分布情况,应采用怎样的方法?[3]
解 (1)要了解全市居民日常用水量的分布情况,统计出大部分居民平均用水量.
(2)采用抽样调查的方式,通过分析样本数据来估计全市居民日常用水量的整体分布情况.
(在例1的情境下)通过抽样调查,获得100位居民2020年的月均用水量(单位:t)如下:
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
(1)列出频率分布表.
(2)画出频率直方图.
(3)由图表可以得到哪些信息?
*(4)如果当地政府希望85%以上的居民每月的用水量不超出标准,根据频率分布表和频率直方图,你能对制定月用水量a提出建议吗?
[规范板书] 解 (1)频率分布表如下:
分组 频数累计 频数 频率
[0,0.5) 4 0.04
[0.5,1) 正 8 0.08
[1,1.5) 正 正 正 15 0.15
[1.5,2) 正 正 正 正 22 0.22
[2,2.5) 正 正 正 正 正 25 0.25
[2.5,3) 正 正 14 0.14
[3,3.5) 正 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1.00
(2) 频率直方图如图所示:
(3)①居民月均用水量的分布是“山峰”状的,而且是“单峰”的;
②大部分居民的月均用水量集中在一个中间值附近,只有少数居民的月均用水量很多或很少;
③居民月均用水量的分布有一定的对称性等.
(4) 由频率分布表知居民的月均用水量小于2.5的频率为0.74,小于3的频率为0.88,所以85%的用水量在[2.5,3)内.由0.74+×0.14=0.85,解得a≈2.89.
因此,月用水量a定为2.89t以上.
一个农技站为了考察某种麦穗长的分布情况,在一块试验地里抽取了100个麦穗,量得长度(单位:cm)如下:
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.6 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
根据上面的数据列出频率分布表,绘出频率直方图,并用自己的语言描述一下这批麦穗长的情况.
[处理建议] 根据前几课时的内容,按照步骤绘制图表,并根据图表作出叙述.
解 具体步骤如下:
①计算极差:7.4-4.0=3.4(cm).
②决定组距与组数.
若取组距为0.3cm,由于=11,需分成12组,组数合适.于是取定组距为0.3cm,组数为12.
③将数据分组.
使分点比数据多一位小数,并且把第1组的起点稍微减小一点,则所分的12个组可以是[3.95,4.25),[4.25,4.55),[4.55,4.85),…,[7.25,7.55].
④列频率分布表.
对各个组作频数累计,然后数频数,算频率,列频率分布表,具体如下:
分组 频数累计 频数 频率
[3.95,4.25) 1 0.01
[4.25,4.55) 1 0.01
[4.55,4.85) 2 0.02
[4.85,5.15) 正 5 0.05
[5.15,5.45) 正 正 11 0.11
[5.45,5.75) 正 正 正 15 0.15
[5.75,6.05) 正 正 正 正 正 28 0.28
[6.05,6.35) 正 正 13 0.13
[6.35,6.65) 正 正 11 0.11
[6.65,6.95) 正 正 10 0.10
[6.95,7.25) 2 0.02
[7.25,7.55] 1 0.01
合 计 100 1
(5)频率直方图如图所示:
从图表中可以看出,绝大部分麦穗长集中在5.15~6.95,并且5.75~6.05占比最大.
按照水果市场的需要等因素,水果种植户把某种成熟后的水果按其直径d(单位:mm)的长度分为不同等级.某商家计划从该种植户处购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下数据:
直径d [18,20) [20,22) [22,24) [24,26) [26,28]
等级 三级品 二级品 一级品 特级品 特级品
频数 1 m 29 n 7
用分层抽样的方法从其中的一级品和特级品中抽取6个,其中一级品2个.
(1)估计这批水果中特级品的比例;
(2)已知样本中这批水果不按等级混装的话20个约1kg,该种植户有20000kg这种水果待售,商家提出两种收购方案:
方案A:以6.5元/kg收购;
方案B:以级别分装收购,每袋20个,特级品8元/袋,一级品5元/袋,二级品4元/袋,三级品3元/袋.
选择哪种方案种植户的收益更高?请说明理由.
解 (1) 由题意得解得m=12,n=51,
所以特级品的频率为=0.58,
可估计这批水果中特级品的比例为58%.
(2)选用方案A,种植户的收益为20000×6.5=130000元;
选用方案B,由题意得种植户的收益为
20000×20××=132000元.
因为132000>130000,所以选择方案B,种植户的收益更高.
某“双一流A类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,调查中有一项是他们的月薪情况.调查发现,他们的月薪在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如图所示的频率直方图.
(1)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前两组中抽出6人,每一组各抽几人?
(2)同一组数据用该组区间的中点值作代表.
①求这100人月薪收入的样本平均数和样本方差s2;
②该校在某地区就业的2018届本科毕业生共50人,决定于2021年国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案1:设Ω=[-s-0.018,+s+0.018),月薪落在区间Ω左侧的每人收取400元,月薪落在区间Ω内的每人收取600元,月薪落在区间Ω右侧的每人收取800元.
方案2:按每人一个月薪水的3%收取.
用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?
参考数据:≈13.2.
解 (1)第一组有0.2×0.1×100=2人,第二组有1.0×0.1×100=10人.
按分层抽样,第一组抽6×=1人,第二组抽6-1=5人.
(2)① 这100人月薪收入的样本平均数=0.02×1.7+0.10×1.8+0.24×1.9+0.31×2+0.2×2.1+0.09×2.2+0.04×2.3=2,
这100人月薪收入的样本方差
s2=0.02×(1.7-2)2+0.10×(1.8-2)2+0.24×(1.9-2)2+0.31×(2-2)2+0.2×(2.1-2)2+0.09×(2.2-2)2+0.04×(2.3-2)2=0.0174.
②方案1:
s===0.132,Ω=[1.85,2.15).
月薪落在区间Ω左侧收活动费用约为(0.02+0.10)×400×50÷10000=0.24万元;
月薪落在区间Ω内收活动费用约为(0.24+0.31+0.20)×600×50÷10000=2.25万元;
月薪落在区间Ω右侧收活动费用约为(0.09+0.04)×800×50÷10000=0.52万元.
因此,选择方案1,这50人共收活动费用约为0.24+2.25+0.52=3.01万元.
选择方案2,这50人共收活动费用约为50×0.03·=3万元.
故方案1能收到更多的费用.
【课堂练习】
1.观察新生婴儿体重的频率直方图(如图),新生婴儿体重在[2700,3000)内的频率为(D)
A.0.001 B.0.1
C.0.2 D.0.3
2.对“小康县”的经济评价标准如下:
①年人均收入不小于7000元;
②年人均食品支出不大于年人均收入的35%.
某县有40万人口,调查数据如下:
年人均收入/元 0 2000 4000 6000 8000 10000 12000 16000
人数/万人 6 3 5 5 6 7 5 3
则该县(B)
A.是小康县
B.达到标准①,未达到标准②,不是小康县
C.达到标准②,未达到标准①,不是小康县
D.两个标准都未达到,不是小康县
提示 年人均收入为7050元,达到标准①;年人均食品支出为2695元,而年人均食品支出占收入的×100%≈38.2%>35%,未达到标准②.故不是小康县.
3.某市4月1日至4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,
88,67,101,103,95,91,77,86,81,83,
82,82,64,79,86,85,75,71,49,45.
(1)列出频率分布表.
(2)画出频率直方图.
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,空间质量为良;在101~150之间时,空间质量为轻微污染;在151~200之间时,空间质量为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
解 (1)频率分布表如下:
分组 频数 频率 分组 频数 频率
[41,51) 2 [81,91) 10
[51,61) 1 [91,101) 5
[61,71) 4 [101,111] 2
[71,81) 6
(2)频率直方图如图所示:
(3)答对下述两条中的一条即可:
①该市一个月中空气污染指数有2天处于优的水平,占当月天数的;有26天处于良的水平,占当月天数的;处于优或良的天数为28,占当月天数的.说明该市空气质量基本良好.
② 轻微污染有2天,占当月天数的;污染指数在80以上的接近轻微污染的天数15,加上处于轻微污染的天数2,占当月天数的,超过50%.这说明该市空气质量有待进一步改善.
【课堂小结】
1.列频率分布表,画频率直方图.
2.用频率直方图估计总体分布.
【教学目标】
1.结合实例,能用样本估计总体的取值规律.
2.能根据频率分布表和频率直方图观测数据的分布规律.
【教学过程】
一、问题情境
情境1:为了实现绿色发展,避免能源浪费,某市政府计划对居民用电采用阶梯收费的方法.为此,相关部门在该市随机调查了200户居民六月份的用电量(单位:kW·h),以了解这个城市家庭用电的情况.
其频率直方图如图所示:
(根据前几课时的学习)为了设计较为合理的收费方法,需要做哪些工作?
答:抽样调查→分析样本数据→通过样本数据来估计全市居民用水量的分布情况.
上图中蕴含了哪些信息?请根据图表归纳居民月均用电量的分布规律.
(答案不唯一,如[80,160]内的数据较多等)
试查阅相关资料,了解阶梯电价产生的背景,以及居民阶梯电价的电量分档和电价确定等相关信息.
情境2:现在很多城市面临交通拥挤的状况,特别是上下班高峰期时堵车现象时有发生.城市交通管理部门需要根据不同时段的车流量制定相应的管理办法.如何了解一天中车流量的分布状况呢?
二、数学建构
假定根据选定的方案实施后已经得到如下数据:
日期 时间段 2日 7日 12日 18日 21日 25日 29日
0:00~1:00 23 76 45 37 58 16 28
1:00~2:00 15 53 24 42 36 38 49
2:00~3:00 5 21 18 32 27 22 7
3:00~4:00 13 9 16 7 22 19 6
4:00~5:00 58 47 33 5 29 49 33
5:00~6:00 129 177 203 111 155 165 223
6:00~7:00 234 327 297 189 332 478 376
7:00~8:00 847 905 786 546 853 769 695
8:00~9:00 632 602 572 412 517 588 666
9:00~10:00 456 524 389 356 438 537 495
10:00~11:00 443 532 478 444 510 473 533
11:00~12:00 556 621 498 568 645 539 678
12:00~13:00 439 322 403 545 552 453 489
13:00~14:00 632 689 599 637 742 599 655
14:00~15:00 237 305 277 203 311 276 347
15:00~16:00 378 403 321 299 415 178 321
16:00~17:00 478 555 393 388 451 279 439
17:00~18:00 732 810 733 684 767 769 822
18:00~19:00 656 698 736 596 693 711 673
19:00~ 20:00 579 621 602 557 562 493 592
20:00~21:00 483 563 521 511 466 461 399
21:00~22:00 221 198 295 254 179 310 265
22:00~23:00 115 89 67 32 123 154 179
23:00~24:00 76 87 48 19 88 121 33
如何根据这个数据样本分析一天中的车流状况呢?(参考情境1)
先用每一时段的车流量数据的平均数估计每个时间段的车流量,得到下表.
时段 0:00~ 1:00 1:00~ 2:00 2:00~ 3:00 3:00~ 4:00 4:00~ 5:00 5:00~ 6:00 6:00~ 7:00 7:00~ 8:00
频数 40 37 19 13 36 166 319 772
频率 0.0047 0.0043 0.0022 0.0015 0.0042 0.0194 0.0372 0.0901
时段 8:00~ 9:00 9:00~ 10:00 10:00~ 11:00 11:00~ 12:00 12:00~ 13:00 13:00~ 14:00 14:00~ 15:00 15:00~ 16:00
频数 570 456 488 586 458 650 279 331
频率 0.0665 0.0532 0.0570 0.0684 0.0535 0.0759 0.0326 0.0386
时段 16:00~ 17:00 17:00~ 18:00 18:00~ 19:00 19:00~ 20:00 20:00~ 21:00 21:00~ 22:00 22:00~ 23:00 23:00~ 24:00
频数 426 760 680 572 486 246 108 67
频率 0.0497 0.0887 0.0794 0.0668 0.0567 0.0287 0.0126 0.0078
(频数合计8565,由于取近似出现误差,频率合计0.9997.)
由此作出频率直方图:
从频率直方图中看出,该路段车流高峰分别为7:00~8:00和17:00~20:00,夜间车流量很小,从5:00起逐步增加.
根据统计结果,可以向相关部门提出怎样的建议?
如:单位错峰上下班、学校错峰上放学等.
三、数学运用
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a(单位:t),用水量不超过a的部分按平价收费,超出a的部分按议价收费.如果大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢?
(1)为了较为合理地确定这个目标,需要做哪些工作?
(2)为了了解全市居民日常用水量的整体分布情况,应采用怎样的方法?[3]
解 (1)要了解全市居民日常用水量的分布情况,统计出大部分居民平均用水量.
(2)采用抽样调查的方式,通过分析样本数据来估计全市居民日常用水量的整体分布情况.
(在例1的情境下)通过抽样调查,获得100位居民2020年的月均用水量(单位:t)如下:
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
(1)列出频率分布表.
(2)画出频率直方图.
(3)由图表可以得到哪些信息?
*(4)如果当地政府希望85%以上的居民每月的用水量不超出标准,根据频率分布表和频率直方图,你能对制定月用水量a提出建议吗?
[规范板书] 解 (1)频率分布表如下:
分组 频数累计 频数 频率
[0,0.5) 4 0.04
[0.5,1) 正 8 0.08
[1,1.5) 正 正 正 15 0.15
[1.5,2) 正 正 正 正 22 0.22
[2,2.5) 正 正 正 正 正 25 0.25
[2.5,3) 正 正 14 0.14
[3,3.5) 正 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1.00
(2) 频率直方图如图所示:
(3)①居民月均用水量的分布是“山峰”状的,而且是“单峰”的;
②大部分居民的月均用水量集中在一个中间值附近,只有少数居民的月均用水量很多或很少;
③居民月均用水量的分布有一定的对称性等.
(4) 由频率分布表知居民的月均用水量小于2.5的频率为0.74,小于3的频率为0.88,所以85%的用水量在[2.5,3)内.由0.74+×0.14=0.85,解得a≈2.89.
因此,月用水量a定为2.89t以上.
一个农技站为了考察某种麦穗长的分布情况,在一块试验地里抽取了100个麦穗,量得长度(单位:cm)如下:
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.6 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
根据上面的数据列出频率分布表,绘出频率直方图,并用自己的语言描述一下这批麦穗长的情况.
[处理建议] 根据前几课时的内容,按照步骤绘制图表,并根据图表作出叙述.
解 具体步骤如下:
①计算极差:7.4-4.0=3.4(cm).
②决定组距与组数.
若取组距为0.3cm,由于=11,需分成12组,组数合适.于是取定组距为0.3cm,组数为12.
③将数据分组.
使分点比数据多一位小数,并且把第1组的起点稍微减小一点,则所分的12个组可以是[3.95,4.25),[4.25,4.55),[4.55,4.85),…,[7.25,7.55].
④列频率分布表.
对各个组作频数累计,然后数频数,算频率,列频率分布表,具体如下:
分组 频数累计 频数 频率
[3.95,4.25) 1 0.01
[4.25,4.55) 1 0.01
[4.55,4.85) 2 0.02
[4.85,5.15) 正 5 0.05
[5.15,5.45) 正 正 11 0.11
[5.45,5.75) 正 正 正 15 0.15
[5.75,6.05) 正 正 正 正 正 28 0.28
[6.05,6.35) 正 正 13 0.13
[6.35,6.65) 正 正 11 0.11
[6.65,6.95) 正 正 10 0.10
[6.95,7.25) 2 0.02
[7.25,7.55] 1 0.01
合 计 100 1
(5)频率直方图如图所示:
从图表中可以看出,绝大部分麦穗长集中在5.15~6.95,并且5.75~6.05占比最大.
按照水果市场的需要等因素,水果种植户把某种成熟后的水果按其直径d(单位:mm)的长度分为不同等级.某商家计划从该种植户处购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下数据:
直径d [18,20) [20,22) [22,24) [24,26) [26,28]
等级 三级品 二级品 一级品 特级品 特级品
频数 1 m 29 n 7
用分层抽样的方法从其中的一级品和特级品中抽取6个,其中一级品2个.
(1)估计这批水果中特级品的比例;
(2)已知样本中这批水果不按等级混装的话20个约1kg,该种植户有20000kg这种水果待售,商家提出两种收购方案:
方案A:以6.5元/kg收购;
方案B:以级别分装收购,每袋20个,特级品8元/袋,一级品5元/袋,二级品4元/袋,三级品3元/袋.
选择哪种方案种植户的收益更高?请说明理由.
解 (1) 由题意得解得m=12,n=51,
所以特级品的频率为=0.58,
可估计这批水果中特级品的比例为58%.
(2)选用方案A,种植户的收益为20000×6.5=130000元;
选用方案B,由题意得种植户的收益为
20000×20××=132000元.
因为132000>130000,所以选择方案B,种植户的收益更高.
某“双一流A类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,调查中有一项是他们的月薪情况.调查发现,他们的月薪在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如图所示的频率直方图.
(1)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前两组中抽出6人,每一组各抽几人?
(2)同一组数据用该组区间的中点值作代表.
①求这100人月薪收入的样本平均数和样本方差s2;
②该校在某地区就业的2018届本科毕业生共50人,决定于2021年国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案1:设Ω=[-s-0.018,+s+0.018),月薪落在区间Ω左侧的每人收取400元,月薪落在区间Ω内的每人收取600元,月薪落在区间Ω右侧的每人收取800元.
方案2:按每人一个月薪水的3%收取.
用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?
参考数据:≈13.2.
解 (1)第一组有0.2×0.1×100=2人,第二组有1.0×0.1×100=10人.
按分层抽样,第一组抽6×=1人,第二组抽6-1=5人.
(2)① 这100人月薪收入的样本平均数=0.02×1.7+0.10×1.8+0.24×1.9+0.31×2+0.2×2.1+0.09×2.2+0.04×2.3=2,
这100人月薪收入的样本方差
s2=0.02×(1.7-2)2+0.10×(1.8-2)2+0.24×(1.9-2)2+0.31×(2-2)2+0.2×(2.1-2)2+0.09×(2.2-2)2+0.04×(2.3-2)2=0.0174.
②方案1:
s===0.132,Ω=[1.85,2.15).
月薪落在区间Ω左侧收活动费用约为(0.02+0.10)×400×50÷10000=0.24万元;
月薪落在区间Ω内收活动费用约为(0.24+0.31+0.20)×600×50÷10000=2.25万元;
月薪落在区间Ω右侧收活动费用约为(0.09+0.04)×800×50÷10000=0.52万元.
因此,选择方案1,这50人共收活动费用约为0.24+2.25+0.52=3.01万元.
选择方案2,这50人共收活动费用约为50×0.03·=3万元.
故方案1能收到更多的费用.
【课堂练习】
1.观察新生婴儿体重的频率直方图(如图),新生婴儿体重在[2700,3000)内的频率为(D)
A.0.001 B.0.1
C.0.2 D.0.3
2.对“小康县”的经济评价标准如下:
①年人均收入不小于7000元;
②年人均食品支出不大于年人均收入的35%.
某县有40万人口,调查数据如下:
年人均收入/元 0 2000 4000 6000 8000 10000 12000 16000
人数/万人 6 3 5 5 6 7 5 3
则该县(B)
A.是小康县
B.达到标准①,未达到标准②,不是小康县
C.达到标准②,未达到标准①,不是小康县
D.两个标准都未达到,不是小康县
提示 年人均收入为7050元,达到标准①;年人均食品支出为2695元,而年人均食品支出占收入的×100%≈38.2%>35%,未达到标准②.故不是小康县.
3.某市4月1日至4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,
88,67,101,103,95,91,77,86,81,83,
82,82,64,79,86,85,75,71,49,45.
(1)列出频率分布表.
(2)画出频率直方图.
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,空间质量为良;在101~150之间时,空间质量为轻微污染;在151~200之间时,空间质量为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
解 (1)频率分布表如下:
分组 频数 频率 分组 频数 频率
[41,51) 2 [81,91) 10
[51,61) 1 [91,101) 5
[61,71) 4 [101,111] 2
[71,81) 6
(2)频率直方图如图所示:
(3)答对下述两条中的一条即可:
①该市一个月中空气污染指数有2天处于优的水平,占当月天数的;有26天处于良的水平,占当月天数的;处于优或良的天数为28,占当月天数的.说明该市空气质量基本良好.
② 轻微污染有2天,占当月天数的;污染指数在80以上的接近轻微污染的天数15,加上处于轻微污染的天数2,占当月天数的,超过50%.这说明该市空气质量有待进一步改善.
【课堂小结】
1.列频率分布表,画频率直方图.
2.用频率直方图估计总体分布.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
