5.3.1 平行线的性质 课件(共23张PPT)
文档属性
| 名称 | 5.3.1 平行线的性质 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 06:47:51 | ||
图片预览







文档简介
(共23张PPT)
人教七下数学同步精品课件
人教版七年级下册
交流预习
2023春人教版七(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
5.3 平行线的性质
5.3.1平行线的性质
第五章 相交线与平行线
核心素养目标:
使学生理解平行线的性质,能初步运用平行线的性质进行有关计算.
通过本节课的教学,培养学生的概括能力和“观察-猜想-证明”的探索方法,培养学生的辩证思维能力和逻辑思维能力.
培养学生的主体意识,向学生渗透讨论的数学思想,培养学生思维的灵活性和广阔性.
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问题 平行线的判定方法是什么?
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
复习引入:
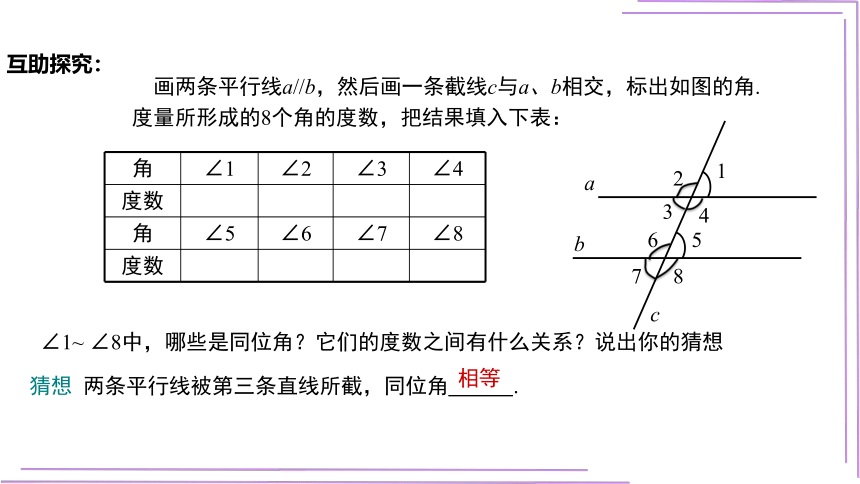
画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
b
1
2
a
c
5
6
7
8
3
4
互助探究:
∠1~ ∠8中,哪些是同位角?它们的度数之间有什么关系?说出你的猜想
猜想 两条平行线被第三条直线所截,同位角___.
相等
a
b
d
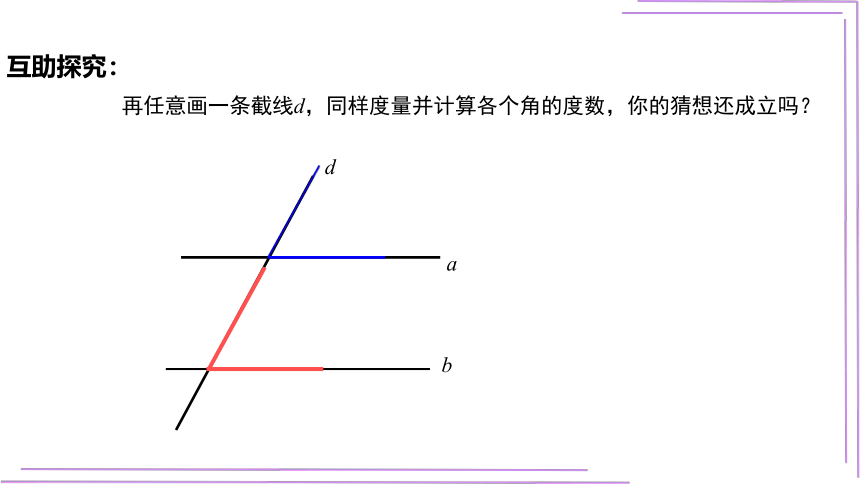
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
互助探究:
两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
新知讲解:
性质1
如图,已知a//b,那么 2与 3相等吗?为什么
解 ∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
互助探究:
思考:在上一节中,我们利用“同位角相等,两直线平行线”推出了“内错角相等,两直线平行线”,类似的,已知两直线平行,同位角相等, 那么能否得到内错角之间的数量关系?
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
新知讲解:
性质2
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: ∵a//b (已知),
∴ 1= 2(两直线平行,同位角相等).
∵ 1+ 4=180°
(邻补角定义),
∴ 2+ 4=180°
(等量代换).
思考:类似的,已知两直线平行,能否可以得到同旁内角之间的数量关系?
互助探究:
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
新知讲解:
性质3
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
思考:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
互助探究:
例1 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:因为梯形上、下底互相平行,所以
∠A与∠D互补, ∠B与∠C互补.
所以梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
例题精讲:
教材20页练习
1.如图,直线a∥b, ∠ 1=54 ,那么∠2、∠3、∠4各是多少度?
1
2
3
4
答:∠2 = ∠ 1=54 ( ),
∠4 = ∠ 1=54 ( ),
∠3=180°-∠4
=180°-54°=126°( )
对顶角相等
两直线平行,同位角相等
邻补角的定义
跟踪练习:
教材20页练习
2.如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°。
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
跟踪练习:
答:(1)DE∥BC,
因为∠ADE=60°,∠B=60°,
所以∠ADE= ∠B.
所以DE∥BC ( )
(2) ∠C =40°.
因为DE∥BC ,
所以∠C = ∠AED.( )
因为∠AED=40°,所以∠C =40°.
同位角相等,两直线平行
两直线平行,同位角相等
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等
简单说成:两直线平行,同位角相等
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补
课堂小结:
教材22页1.如图,一条公路两次拐弯前后两条路互相平行.第一次拐的∠B是142°,第二次拐的∠C是多少度?为什么?
解:∠C=142o
∵两直线平行,内错角相等.
B
C
课堂检测:
教材22页3.如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度,为什么?
(2)从∠1=110o可以知道 ∠3是多少度,为什么?
(3)从 ∠1=110o可以知道∠4 是多少度,为什么?
2
3
E
1
4
A
B
D
C
解:(1)∠2=110o
∵两直线行,内错角相等;
(2)∠3=110o
∵两直线平行, 同位角相等;
(3)∠4=70o
∵两直线平行,同旁内角互补.
课堂检测:
教材24页8. 光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1=45°,∠2=122°,求图中其他角的度数.
课堂检测:
解:由题意得:
∠3 =∠1 = 45°,∠1+∠7 = 180°,∴∠7 = 180°-∠1 = 135°.
∴∠8 =∠7 = 135°.
又∠4 =∠2 = 122°,∠2 +∠5 = 180°,∴∠5 = 180°-∠2 = 58°.
∴∠6=∠5=58°.
课后作业:
必做题:P23习题5.3第5、6;
选做题:P23习题5.3第7题 .
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七下数学同步精品课件
人教版七年级下册
交流预习
2023春人教版七(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
5.3 平行线的性质
5.3.1平行线的性质
第五章 相交线与平行线
核心素养目标:
使学生理解平行线的性质,能初步运用平行线的性质进行有关计算.
通过本节课的教学,培养学生的概括能力和“观察-猜想-证明”的探索方法,培养学生的辩证思维能力和逻辑思维能力.
培养学生的主体意识,向学生渗透讨论的数学思想,培养学生思维的灵活性和广阔性.
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问题 平行线的判定方法是什么?
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
复习引入:
画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
b
1
2
a
c
5
6
7
8
3
4
互助探究:
∠1~ ∠8中,哪些是同位角?它们的度数之间有什么关系?说出你的猜想
猜想 两条平行线被第三条直线所截,同位角___.
相等
a
b
d
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
互助探究:
两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
新知讲解:
性质1
如图,已知a//b,那么 2与 3相等吗?为什么
解 ∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
互助探究:
思考:在上一节中,我们利用“同位角相等,两直线平行线”推出了“内错角相等,两直线平行线”,类似的,已知两直线平行,同位角相等, 那么能否得到内错角之间的数量关系?
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
新知讲解:
性质2
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: ∵a//b (已知),
∴ 1= 2(两直线平行,同位角相等).
∵ 1+ 4=180°
(邻补角定义),
∴ 2+ 4=180°
(等量代换).
思考:类似的,已知两直线平行,能否可以得到同旁内角之间的数量关系?
互助探究:
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
新知讲解:
性质3
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
思考:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
互助探究:
例1 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:因为梯形上、下底互相平行,所以
∠A与∠D互补, ∠B与∠C互补.
所以梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
例题精讲:
教材20页练习
1.如图,直线a∥b, ∠ 1=54 ,那么∠2、∠3、∠4各是多少度?
1
2
3
4
答:∠2 = ∠ 1=54 ( ),
∠4 = ∠ 1=54 ( ),
∠3=180°-∠4
=180°-54°=126°( )
对顶角相等
两直线平行,同位角相等
邻补角的定义
跟踪练习:
教材20页练习
2.如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°。
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
跟踪练习:
答:(1)DE∥BC,
因为∠ADE=60°,∠B=60°,
所以∠ADE= ∠B.
所以DE∥BC ( )
(2) ∠C =40°.
因为DE∥BC ,
所以∠C = ∠AED.( )
因为∠AED=40°,所以∠C =40°.
同位角相等,两直线平行
两直线平行,同位角相等
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等
简单说成:两直线平行,同位角相等
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补
课堂小结:
教材22页1.如图,一条公路两次拐弯前后两条路互相平行.第一次拐的∠B是142°,第二次拐的∠C是多少度?为什么?
解:∠C=142o
∵两直线平行,内错角相等.
B
C
课堂检测:
教材22页3.如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度,为什么?
(2)从∠1=110o可以知道 ∠3是多少度,为什么?
(3)从 ∠1=110o可以知道∠4 是多少度,为什么?
2
3
E
1
4
A
B
D
C
解:(1)∠2=110o
∵两直线行,内错角相等;
(2)∠3=110o
∵两直线平行, 同位角相等;
(3)∠4=70o
∵两直线平行,同旁内角互补.
课堂检测:
教材24页8. 光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1=45°,∠2=122°,求图中其他角的度数.
课堂检测:
解:由题意得:
∠3 =∠1 = 45°,∠1+∠7 = 180°,∴∠7 = 180°-∠1 = 135°.
∴∠8 =∠7 = 135°.
又∠4 =∠2 = 122°,∠2 +∠5 = 180°,∴∠5 = 180°-∠2 = 58°.
∴∠6=∠5=58°.
课后作业:
必做题:P23习题5.3第5、6;
选做题:P23习题5.3第7题 .
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
