第5章 相交线与平行线 小结与复习 课件(共27张PPT)
文档属性
| 名称 | 第5章 相交线与平行线 小结与复习 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 06:50:22 | ||
图片预览








文档简介
(共27张PPT)
人教七下数学同步精品课件
人教版七年级下册
交流预习
2023春人教版七(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第五章 相交线与平行线
小结与复习
第五章 相交线与平行线
核心素养目标:
通过思考与操作相结合的回顾与反思,进一步加深对本章内容的学习。
经过观察、操作、想象、交流等过程,进一步发展空间观念;进一步体会知识点之间的联系。
复习本章学过的知识要点,说出各知识点之间的关系,巩固所学的知识,并能用这些知识解决一些问题。提高逻辑思维能力;进一步发展有条理地思考和表达的能力。
复习引入:
本章我们学面内不重合的两条直线的位置关系一一相交与平行.当两条直线只有一个公共点时,这两条直线相交。在相交线的学习中,我们研究了两条直线相交所形成的邻补角和对顶角的位置和数量关系,这也是相交线的性质。垂直是相交的特殊情形,它在实际生产和社会生活中具有广泛的应用当两条直线没有公共点时,这两条直线平行,借助两条直线被第三条直线所截形成的同位角、内错角和同旁内角,我们研究了平行线的判定与性质.
“图形的判定”讨论的是确定某种图形需要什么条件,例如,两条直线与第三条直线相交,具备“同位角相等”,就有“两直线平行”。“图形的性质讨论的是这类图形有怎样的共同特性,例如,两条直线只要平行,它们被第三条直线所截时,就一定有同位角相等.
学习本章时,要注意观察实物、模型和图形,通过观察、测量、实验、归纳、对比、类比等来寻找图形中的位置关系和数量关系,从而发现图形的性质,同时,还要注意体会通过“推理”获得数学结论的方法,培养言之有据的习惯和有条理地思考、表达的能力.
交流预习:
请你带着下面的问题,复习一下全章的内容吧。
1.下面是本章学到的一些数学名词,你能用自己的语言描述它们吗 你能分别画一个图形表示它们吗
对顶角、邻补角、垂直、平行、同位角、内错角、同旁内角、平移。
2.两条直线相交形成四个角,它们具有怎样的位置关系和数量关系
3.什么是点到直线的距离 你会度量吗 请举例说明.
4.怎样判定两条直线是否平行 平行线有什么性质 对比平行线的性质和直线平行的判定方法,它们有什么异同
5.什么是命题 如何判断一个命题是真命题还是假命题 请结合具体例子说明.
6.图形平移时,连接各对应点的线段有什么关系 你能利用平移设计一些图案吗
1. 判断题(正确的画√,错误的画×).
(1)a,b,c是直线,若a∥b,b∥c,则a∥c;( ) (2)a,b,c是直线,若a⊥b,b⊥c,则a⊥c.( )
提示:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行.如果没有“在同一平面内”这个前提条件,则不一定平行,有可能垂直.
√
×
课堂训练:
知识点一 相交线
2.如图,两条直线 a,b 相交.
(1)如果∠1 = 60°,求∠2,∠3,∠4 的度数;
(2)如果2∠3 = 3∠1,求∠2,∠3,∠4 的度数.
课堂训练:
解:(1)∠2 = 180°-∠1 = 180°-60°= 120°(邻补角定义).
∠3 =∠2 = 120°(对顶角相等).
∠4 =∠1 = 60°(对顶角相等).
(2)∵∠1+∠3=180°,又2∠3=3∠1,即∠1= ∠3,∴ ∠3+∠3 = 180°, ∠3 = 180°,∠3 = 108°,∠2 =∠3 = 108°(对顶角相等),∠4 = 180°-∠3 = 180°-108°= 72°(邻补角定义).
知识点一 相交线
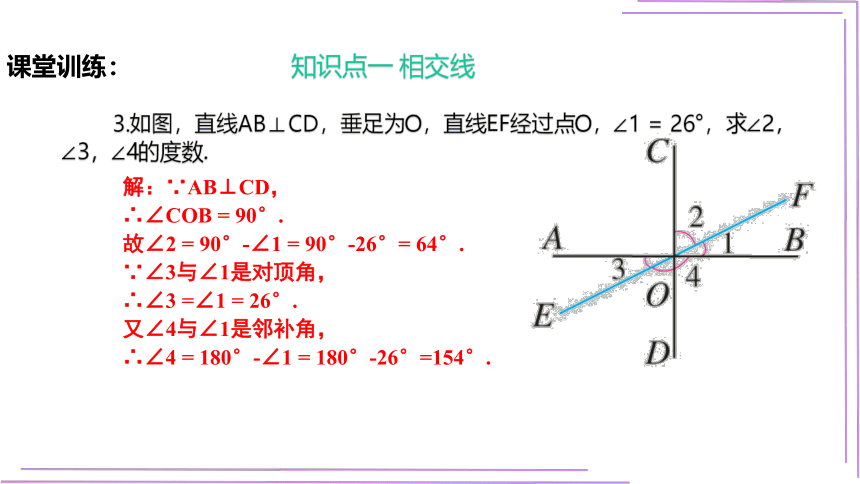
3.如图,直线AB⊥CD,垂足为O,直线EF经过点O,∠1 = 26°,求∠2,∠3,∠4的度数.
解:∵AB⊥CD,
∴∠COB = 90°.
故∠2 = 90°-∠1 = 90°-26°= 64°.
∵∠3与∠1是对顶角,
∴∠3 =∠1 = 26°.
又∠4与∠1是邻补角,
∴∠4 = 180°-∠1 = 180°-26°=154°.
课堂训练:
知识点一 相交线
4. 根据下列语句画出图形:
(1)过线段 AB 的中点 C ,画 CD⊥AB ;
(2)点 P 到直线 AB 的距离是3cm,过点 P 画直线 AB 的垂线 PC ;
(3)过三角形 ABC 内的一点 P,分别画 AB,BC,CA的平行线.
课堂训练:
解:如图:
知识点二 点到直线的距离
5. 如图,某人骑自行车自 A 沿正东方向前进,至 B 处后,行驶方向改为东偏南15°,行驶到C 处仍按正东方向行驶,画出继续行驶的路线.
解:如图所示:
A
B
15°
课堂训练:
知识点三 平行线的性质和判定
6.如图∠1 = 30°,∠B = 60°,AB⊥AC.
(1)∠DAB +∠B 等于多少度?
(2)AD 与 BC 平行吗?AB 与CD 平行吗?
解:(1)∵AB⊥AC,∴∠2 = 90°.
则∠DAB +∠B =∠1 + ∠2 + ∠B
= 30°+ 90°+ 60°= 180°.
2
课堂训练:
(2)由(1)∠DAB +∠B = 180°,得AD∥BC(同旁内角互补,两直线平行).
AB与CD不一定平行,如图中虚线所示.
知识点三 平行线的性质和判定
7.如图,平行线 a,b 被直线 c 所截,知道∠1~∠8 中一个角的度数,能否求出其他角的度数?如果能,用其中一个角表示出其他各角.
课堂训练:
解:知道∠1~∠8中的一个角的度数,能求出其他角的度数,如用∠1表示其他各角. ∠2 = 180°-∠1,∠3 = ∠1,∠4 = 180°-∠1,∠5 =∠1,∠6 = 180°-∠1,∠7 =∠1,∠8 = 180°-∠1.
知识点三 平行线的性质和判定
8.选择题.
(1)如图(1),点 E 在 AC 的延长线上,下列条件中能判断 AB∥CD 的是( ).
(A)∠3=∠4
(B)∠1=∠2
(C)∠D =∠DCE
(D)∠D +∠ACD = 180°
可得出BD∥AC,而不是AB∥CD.
B
可判断出BD∥AC.
可判断出BD∥AC.
可得AB∥CD.
(1)
课堂训练:
知识点三 平行线的性质和判定
(2)如图(2),∠1 +∠2 = 180°,∠3 = 108°,则∠4 的度数是( ).
(A)72°
(B)80°
(C)82°
(D)108°
A
(2)
课堂训练:
知识点三 平行线的性质和判定
9. 图中所示为一组护网的示意图,它可看成由两组平行线组成,你能通过检验一些角的大小来判断其中的线段是否平行吗?说出你的理由.
解:可根据内错角相等,两直线平行,也可以利用同位角相等,两直线平行;同旁内角互补,两直线平行等来判断.
课堂训练:
知识点三 平行线的性质和判定
10. 如图,∠AOB 内有一点 P :
(1)过点 P 画出 PC∥OB 交 OA 于点 C,画 PD∥OA 交 OB 于点 D;
(2)写出图中互补的角;
(3)写出图中相等的角.
解:(1)如图所示.
①∠1=∠O =∠6=∠4=∠8=∠10;
②∠2=∠3=∠5=∠7=∠9.
A
B
O
P
4
3
6
5
10
7
8
9
1
2
D
C
(2)①中任一个角与②中任一个角互补.
(3)①中的角与②中的角各分别相等.
课堂训练:
知识点三 平行线的性质和判定
证明:∵DE∥BA,
∴∠FDE=_____ ( ).
∵DF∥CA,
∴∠A=_____ ( ).
∴∠FDE=∠A.
(1)
∠BFD
两直线平行,内错角相等
∠BFD
两直线平行,同位角相等
课堂训练:
13.完成下面的证明.
(1)如图(1),点 D,E,F 分别是三角形ABC 的边 BC,CA,AB 上的一点,DE∥BA,DF∥CA.求证∠FDE =∠A.
知识点三 平行线的性质和判定
(2)如图(2),AB 和 CD 相交于点 O,∠C =∠COA,∠D =∠BOD . 求证 AC∥BD .
(2)
课堂训练:
证明:∵∠C =∠COA,∠D =∠BOD,
又∠COA =∠BOD( 对顶角相等),
∴∠C = ___∠D___.
∴AC∥BD( ).
内错角相等,两直线平行
知识点三 平行线的性质和判定
15.一个台球桌的桌面如图所示,一个球在桌面上的点A滚向桌边PQ,碰着PQ上的点B后便反弹而滚向桌边RS,碰到RS上的点C便反弹而滚向点D.如果PQ∥RS,AB,BC,CD都是直线,且∠ABC的平分线BN垂直于PQ,∠BCD的平分线CM垂直于RS,那么,球经过两次反弹后所滚的路径CD是否平行于原来的路径AB?
A
S
A
B
N
M
C
D
Q
R
解:如图所示:CD∥AB.
理由如下:
∵QP∥RS,
∴∠1=∠6(两直线平行,内错 角相等).
又BN⊥QP,MC⊥RS,
∴∠1+∠3=90°,∠8+∠6=90°.
∴∠3=∠8(等角的余角相等).
课堂训练:
知识点三 平行线的性质和判定
由BN⊥QP可知
∠1+∠3=∠2+∠4=90°.
又由BN平分∠ABC,∴∠3=∠4.
同理可得∠7=∠8.
∴∠3+∠4 = 2∠3,∠7+∠8
= 2∠8,
∴∠3+∠4 = ∠7+∠8.
即∠CBA=∠DCB,
∴AB∥CD(内错角相等,两直线平行).
课堂训练:
知识点三 平行线的性质和判定
11.如图,利用平移可以画出一些立体图形.在方格纸上写出你的名字或你的校名,用类似的方法画出它的立体图.变换不同的长度和方向多试几次,你认为哪一种更艺术效果?
课堂训练:
知识点四 平移
12.指出下列命题的题设和结论,并判断它们是真命题还是假命题.如果是假命题,举出一个反例.
(1)两个角的和等于平角时,这两个角互为补角;
(2)内错角相等;
(3)两条平行线被第三条直线所截,内错角相等.
假命题
假命题
真命题
课堂训练:
专题五 命题
相交线
平行线
垂线
两条
直线
相交
两条直线被
第三条所截
一般情况
相交成直角
邻补角
对顶角
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行公理及其推论
平移
平移的特征
邻补角互补
对顶角相等
平行线的判定
平行线的性质
本章知识结构图:
课后作业:
本章单元测试卷
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七下数学同步精品课件
人教版七年级下册
交流预习
2023春人教版七(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第五章 相交线与平行线
小结与复习
第五章 相交线与平行线
核心素养目标:
通过思考与操作相结合的回顾与反思,进一步加深对本章内容的学习。
经过观察、操作、想象、交流等过程,进一步发展空间观念;进一步体会知识点之间的联系。
复习本章学过的知识要点,说出各知识点之间的关系,巩固所学的知识,并能用这些知识解决一些问题。提高逻辑思维能力;进一步发展有条理地思考和表达的能力。
复习引入:
本章我们学面内不重合的两条直线的位置关系一一相交与平行.当两条直线只有一个公共点时,这两条直线相交。在相交线的学习中,我们研究了两条直线相交所形成的邻补角和对顶角的位置和数量关系,这也是相交线的性质。垂直是相交的特殊情形,它在实际生产和社会生活中具有广泛的应用当两条直线没有公共点时,这两条直线平行,借助两条直线被第三条直线所截形成的同位角、内错角和同旁内角,我们研究了平行线的判定与性质.
“图形的判定”讨论的是确定某种图形需要什么条件,例如,两条直线与第三条直线相交,具备“同位角相等”,就有“两直线平行”。“图形的性质讨论的是这类图形有怎样的共同特性,例如,两条直线只要平行,它们被第三条直线所截时,就一定有同位角相等.
学习本章时,要注意观察实物、模型和图形,通过观察、测量、实验、归纳、对比、类比等来寻找图形中的位置关系和数量关系,从而发现图形的性质,同时,还要注意体会通过“推理”获得数学结论的方法,培养言之有据的习惯和有条理地思考、表达的能力.
交流预习:
请你带着下面的问题,复习一下全章的内容吧。
1.下面是本章学到的一些数学名词,你能用自己的语言描述它们吗 你能分别画一个图形表示它们吗
对顶角、邻补角、垂直、平行、同位角、内错角、同旁内角、平移。
2.两条直线相交形成四个角,它们具有怎样的位置关系和数量关系
3.什么是点到直线的距离 你会度量吗 请举例说明.
4.怎样判定两条直线是否平行 平行线有什么性质 对比平行线的性质和直线平行的判定方法,它们有什么异同
5.什么是命题 如何判断一个命题是真命题还是假命题 请结合具体例子说明.
6.图形平移时,连接各对应点的线段有什么关系 你能利用平移设计一些图案吗
1. 判断题(正确的画√,错误的画×).
(1)a,b,c是直线,若a∥b,b∥c,则a∥c;( ) (2)a,b,c是直线,若a⊥b,b⊥c,则a⊥c.( )
提示:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行.如果没有“在同一平面内”这个前提条件,则不一定平行,有可能垂直.
√
×
课堂训练:
知识点一 相交线
2.如图,两条直线 a,b 相交.
(1)如果∠1 = 60°,求∠2,∠3,∠4 的度数;
(2)如果2∠3 = 3∠1,求∠2,∠3,∠4 的度数.
课堂训练:
解:(1)∠2 = 180°-∠1 = 180°-60°= 120°(邻补角定义).
∠3 =∠2 = 120°(对顶角相等).
∠4 =∠1 = 60°(对顶角相等).
(2)∵∠1+∠3=180°,又2∠3=3∠1,即∠1= ∠3,∴ ∠3+∠3 = 180°, ∠3 = 180°,∠3 = 108°,∠2 =∠3 = 108°(对顶角相等),∠4 = 180°-∠3 = 180°-108°= 72°(邻补角定义).
知识点一 相交线
3.如图,直线AB⊥CD,垂足为O,直线EF经过点O,∠1 = 26°,求∠2,∠3,∠4的度数.
解:∵AB⊥CD,
∴∠COB = 90°.
故∠2 = 90°-∠1 = 90°-26°= 64°.
∵∠3与∠1是对顶角,
∴∠3 =∠1 = 26°.
又∠4与∠1是邻补角,
∴∠4 = 180°-∠1 = 180°-26°=154°.
课堂训练:
知识点一 相交线
4. 根据下列语句画出图形:
(1)过线段 AB 的中点 C ,画 CD⊥AB ;
(2)点 P 到直线 AB 的距离是3cm,过点 P 画直线 AB 的垂线 PC ;
(3)过三角形 ABC 内的一点 P,分别画 AB,BC,CA的平行线.
课堂训练:
解:如图:
知识点二 点到直线的距离
5. 如图,某人骑自行车自 A 沿正东方向前进,至 B 处后,行驶方向改为东偏南15°,行驶到C 处仍按正东方向行驶,画出继续行驶的路线.
解:如图所示:
A
B
15°
课堂训练:
知识点三 平行线的性质和判定
6.如图∠1 = 30°,∠B = 60°,AB⊥AC.
(1)∠DAB +∠B 等于多少度?
(2)AD 与 BC 平行吗?AB 与CD 平行吗?
解:(1)∵AB⊥AC,∴∠2 = 90°.
则∠DAB +∠B =∠1 + ∠2 + ∠B
= 30°+ 90°+ 60°= 180°.
2
课堂训练:
(2)由(1)∠DAB +∠B = 180°,得AD∥BC(同旁内角互补,两直线平行).
AB与CD不一定平行,如图中虚线所示.
知识点三 平行线的性质和判定
7.如图,平行线 a,b 被直线 c 所截,知道∠1~∠8 中一个角的度数,能否求出其他角的度数?如果能,用其中一个角表示出其他各角.
课堂训练:
解:知道∠1~∠8中的一个角的度数,能求出其他角的度数,如用∠1表示其他各角. ∠2 = 180°-∠1,∠3 = ∠1,∠4 = 180°-∠1,∠5 =∠1,∠6 = 180°-∠1,∠7 =∠1,∠8 = 180°-∠1.
知识点三 平行线的性质和判定
8.选择题.
(1)如图(1),点 E 在 AC 的延长线上,下列条件中能判断 AB∥CD 的是( ).
(A)∠3=∠4
(B)∠1=∠2
(C)∠D =∠DCE
(D)∠D +∠ACD = 180°
可得出BD∥AC,而不是AB∥CD.
B
可判断出BD∥AC.
可判断出BD∥AC.
可得AB∥CD.
(1)
课堂训练:
知识点三 平行线的性质和判定
(2)如图(2),∠1 +∠2 = 180°,∠3 = 108°,则∠4 的度数是( ).
(A)72°
(B)80°
(C)82°
(D)108°
A
(2)
课堂训练:
知识点三 平行线的性质和判定
9. 图中所示为一组护网的示意图,它可看成由两组平行线组成,你能通过检验一些角的大小来判断其中的线段是否平行吗?说出你的理由.
解:可根据内错角相等,两直线平行,也可以利用同位角相等,两直线平行;同旁内角互补,两直线平行等来判断.
课堂训练:
知识点三 平行线的性质和判定
10. 如图,∠AOB 内有一点 P :
(1)过点 P 画出 PC∥OB 交 OA 于点 C,画 PD∥OA 交 OB 于点 D;
(2)写出图中互补的角;
(3)写出图中相等的角.
解:(1)如图所示.
①∠1=∠O =∠6=∠4=∠8=∠10;
②∠2=∠3=∠5=∠7=∠9.
A
B
O
P
4
3
6
5
10
7
8
9
1
2
D
C
(2)①中任一个角与②中任一个角互补.
(3)①中的角与②中的角各分别相等.
课堂训练:
知识点三 平行线的性质和判定
证明:∵DE∥BA,
∴∠FDE=_____ ( ).
∵DF∥CA,
∴∠A=_____ ( ).
∴∠FDE=∠A.
(1)
∠BFD
两直线平行,内错角相等
∠BFD
两直线平行,同位角相等
课堂训练:
13.完成下面的证明.
(1)如图(1),点 D,E,F 分别是三角形ABC 的边 BC,CA,AB 上的一点,DE∥BA,DF∥CA.求证∠FDE =∠A.
知识点三 平行线的性质和判定
(2)如图(2),AB 和 CD 相交于点 O,∠C =∠COA,∠D =∠BOD . 求证 AC∥BD .
(2)
课堂训练:
证明:∵∠C =∠COA,∠D =∠BOD,
又∠COA =∠BOD( 对顶角相等),
∴∠C = ___∠D___.
∴AC∥BD( ).
内错角相等,两直线平行
知识点三 平行线的性质和判定
15.一个台球桌的桌面如图所示,一个球在桌面上的点A滚向桌边PQ,碰着PQ上的点B后便反弹而滚向桌边RS,碰到RS上的点C便反弹而滚向点D.如果PQ∥RS,AB,BC,CD都是直线,且∠ABC的平分线BN垂直于PQ,∠BCD的平分线CM垂直于RS,那么,球经过两次反弹后所滚的路径CD是否平行于原来的路径AB?
A
S
A
B
N
M
C
D
Q
R
解:如图所示:CD∥AB.
理由如下:
∵QP∥RS,
∴∠1=∠6(两直线平行,内错 角相等).
又BN⊥QP,MC⊥RS,
∴∠1+∠3=90°,∠8+∠6=90°.
∴∠3=∠8(等角的余角相等).
课堂训练:
知识点三 平行线的性质和判定
由BN⊥QP可知
∠1+∠3=∠2+∠4=90°.
又由BN平分∠ABC,∴∠3=∠4.
同理可得∠7=∠8.
∴∠3+∠4 = 2∠3,∠7+∠8
= 2∠8,
∴∠3+∠4 = ∠7+∠8.
即∠CBA=∠DCB,
∴AB∥CD(内错角相等,两直线平行).
课堂训练:
知识点三 平行线的性质和判定
11.如图,利用平移可以画出一些立体图形.在方格纸上写出你的名字或你的校名,用类似的方法画出它的立体图.变换不同的长度和方向多试几次,你认为哪一种更艺术效果?
课堂训练:
知识点四 平移
12.指出下列命题的题设和结论,并判断它们是真命题还是假命题.如果是假命题,举出一个反例.
(1)两个角的和等于平角时,这两个角互为补角;
(2)内错角相等;
(3)两条平行线被第三条直线所截,内错角相等.
假命题
假命题
真命题
课堂训练:
专题五 命题
相交线
平行线
垂线
两条
直线
相交
两条直线被
第三条所截
一般情况
相交成直角
邻补角
对顶角
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行公理及其推论
平移
平移的特征
邻补角互补
对顶角相等
平行线的判定
平行线的性质
本章知识结构图:
课后作业:
本章单元测试卷
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
