1.5.2 平方差公式(第2课时)课件(共24张PPT)
文档属性
| 名称 | 1.5.2 平方差公式(第2课时)课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-14 22:47:48 | ||
图片预览







文档简介
(共24张PPT)
1.5.2平方差公式(第2课时)
第一章
整式的乘除
北师大版七年级下册
学习目标
1.掌握平方差公式的结构特征,能运用公式进行简
便运算;
2.会用几何图形说明公式的意义,体会数形结合的
思想方法.
情境导入
1.平方差公式:(a+b)(a-b)=a2-b2
2.公式的结构特点:
左边是两个二项式的乘积,即两数和与这两数差的积;右边是两数的平方差。
3.利用平方差公式计算:
(1)(2x+7b)(2x–7b);
(2)(-m+3n)(m+3n).
4x2-49b2
9n2-m2
情境导入
某同学在计算97×103时将其变成(100-3)(100+3)
并很快得出结果,你知道他运用了什么知识吗?这节
课我们一起来探讨上述计算的规律.
探究新知
核心知识点一:
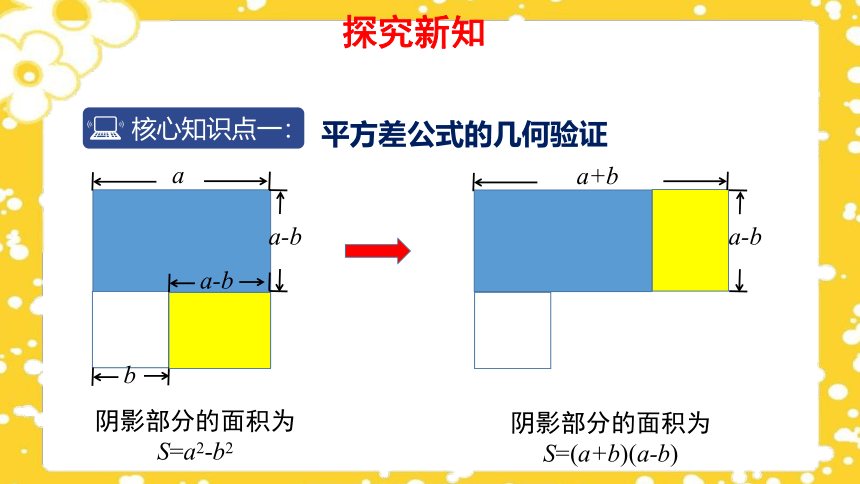
平方差公式的几何验证
a
b
a-b
a-b
阴影部分的面积为
S=a2-b2
阴影部分的面积为
S=(a+b)(a-b)
a+b
a-b
探究新知
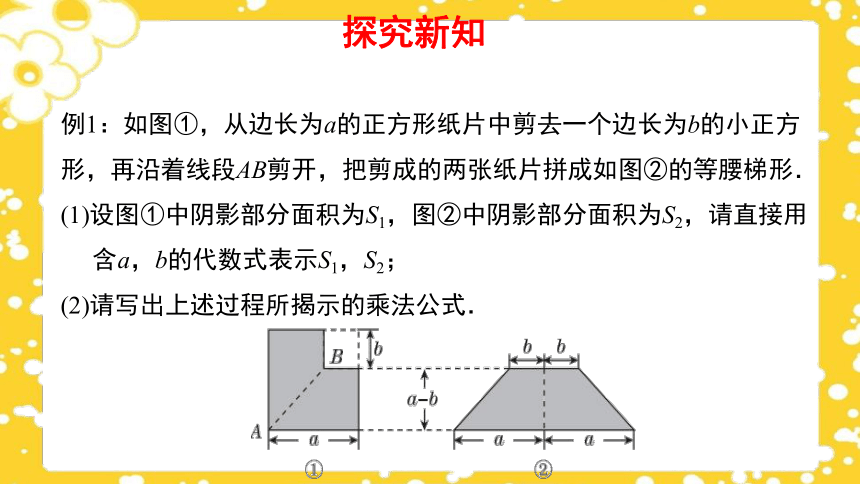
例1:如图①,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸片拼成如图②的等腰梯形.
(1)设图①中阴影部分面积为S1,图②中阴影部分面积为S2,请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式.
探究新知
分析:直先计算图①中阴影部分面积为S1=a2-b2,再计算图②中阴影部分面积为S2= (2b+2a) (a-b),然后根据面积相等得到乘法公式.
解:(1) S1=a2-b2,
S2= (2b+2a)(a-b) =(a+b)(a-b).
(2) (a+b)(a-b)= a2-b2.
探究新知
核心知识点二:
平方差公式的运用
相邻两个自然数的乘积
(1)计算下列各组算式,并观察它们的特点
63
64
143
144
6399
6400
一个自然数的平方比它相邻两数的积大1
探究新知
是不是大于1的所有自然数都有这个特点呢?
你能用字母表示这一规律吗?
设这个自然数为a,与它相邻的两个自然数为a-1,a+1,
则有(a+1)(a-1)=a2-1.
例题讲解
例2 用平方差公式进行计算:
(1)103×97; (2)118×122.
解:(1)103×97
=(100+3) (100-3)
=1002-32
=9 991 ;
(2)118×122
=(120-2) (100+2)
=1202-22
=14 396 .
关键:
a为两数和的平均数;
b为|两数差|的平均数
例3:计算:
(1)a2 (a+b)(a-b)+a2 b2
(2)(2x-5)(2x+5)-2x(2x-3)
解: (1)a2 (a+b)(a-b)+a2 b2
=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4
(2)(2x-5)(2x+5)-2x(2x-3)
=4x2-52-(4x2-6x)
=4x2-25-4x2+6x
=6x-25
不符合平方差公式运算条件的乘法,按乘法法则进行运算.
例题讲解
例4:公式的逆用
(1)(x+y)2-(x-y)2 (2)252-242
分析:逆用平方差公式可以使运算简便.
解:(1)(x+y)2-(x-y)2
=[(x+y)+(x-y)][(x+y)-(x-y)]
=2x·2y
=4xy
(2)252-242
=(25+24)(25-24)
=49
例题讲解
解:李大妈吃亏了.理由如下:原正方形的面积为a2,改变边长后面积为(a+4)(a-4)=a2-16.
∵a2>a2-16,
∴李大妈吃亏了.
例5. 王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
例题讲解
随堂练习
1. 将图甲中阴影部分的小长方形变换到图乙位置,根据两个图形的面积关系可以得到一个关于a,b的恒等式为( )
A.(a-b)2=a2-2ab+b2 B.(a+b)2=a2+2ab+b2
C.(a+b)(a-b)=a2-b2 D.a(a-b)=a2-ab
C
随堂练习
2.如图,在边长为a的正方形中裁掉一个边长为b的小正方形(如图1),将剩余部分沿虚线剪开后拼接(如图2),通过计算,用拼接前后两个图形中阴影部分的面积可以验证等式( )
A.a2-b2=(a+b)(a-b)
B.(a+b)2=a2+2ab+b2
C.(a+2b)(a-b)=a2+ab-2b2
D.(a-b)2=a2-2ab+b2
A
随堂练习
3.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的长方形.根据图形的变化过程写出的一个正确的等式是( )
A.a(a-b)=a2-ab
B.(a-b)2=a2-2ab+b2
C.(a-b)2=a2-b2
D.a2-b2=(a+b)(a-b)
D
随堂练习
4. 计算2 0162-2 015×2 017的结果是( )
A.1 B.-1
C.2 D.-2
A
5.(x+6)(x-6)-x(x-9)=0的解是______.
x=4
随堂练习
6.(1)如图①,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)若将阴影部分裁剪下来,重新拼成一个长方形,如图②,则这个长方形的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图①②中阴影部分的面积,
可以得到什么结论
a2-b2
a-b
a+b
(a+b)(a-b)
结论:(a+b)(a-b)=a2-b2.
随堂练习
7. 填空:
(1)已知(x-a)(x+a)=x2-9,则a的值为________;
(2)若(m+4x)(m-4x)=36-nx2,则mn的值为________.
±96
±3
8. 97×103=_______________=______________=
________________=_______________.
(100-3)(100+3)
1002-9
10000-9
9991
随堂练习
9. 请先观察下列算式,再填空:
32-12=8×1,52-32=8×2.
①72-52=8×______;
②92-(_____)2=8×4;
③(_____)2-92=8×5;
④132-(_____)2=8×______;
….
3
7
11
11
6
随堂练习
10.计算:
(1)102×98(用简便方法计算); (2)(x-1)(x+1)(x2+1).
解:原式=(100+2)(100-2)
=1002-22
=10 000-4
=9 996
解:原式=(x2-1)(x2+1)
=(x2)2-12
=x4-1
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5.2平方差公式(第2课时)
第一章
整式的乘除
北师大版七年级下册
学习目标
1.掌握平方差公式的结构特征,能运用公式进行简
便运算;
2.会用几何图形说明公式的意义,体会数形结合的
思想方法.
情境导入
1.平方差公式:(a+b)(a-b)=a2-b2
2.公式的结构特点:
左边是两个二项式的乘积,即两数和与这两数差的积;右边是两数的平方差。
3.利用平方差公式计算:
(1)(2x+7b)(2x–7b);
(2)(-m+3n)(m+3n).
4x2-49b2
9n2-m2
情境导入
某同学在计算97×103时将其变成(100-3)(100+3)
并很快得出结果,你知道他运用了什么知识吗?这节
课我们一起来探讨上述计算的规律.
探究新知
核心知识点一:
平方差公式的几何验证
a
b
a-b
a-b
阴影部分的面积为
S=a2-b2
阴影部分的面积为
S=(a+b)(a-b)
a+b
a-b
探究新知
例1:如图①,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸片拼成如图②的等腰梯形.
(1)设图①中阴影部分面积为S1,图②中阴影部分面积为S2,请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式.
探究新知
分析:直先计算图①中阴影部分面积为S1=a2-b2,再计算图②中阴影部分面积为S2= (2b+2a) (a-b),然后根据面积相等得到乘法公式.
解:(1) S1=a2-b2,
S2= (2b+2a)(a-b) =(a+b)(a-b).
(2) (a+b)(a-b)= a2-b2.
探究新知
核心知识点二:
平方差公式的运用
相邻两个自然数的乘积
(1)计算下列各组算式,并观察它们的特点
63
64
143
144
6399
6400
一个自然数的平方比它相邻两数的积大1
探究新知
是不是大于1的所有自然数都有这个特点呢?
你能用字母表示这一规律吗?
设这个自然数为a,与它相邻的两个自然数为a-1,a+1,
则有(a+1)(a-1)=a2-1.
例题讲解
例2 用平方差公式进行计算:
(1)103×97; (2)118×122.
解:(1)103×97
=(100+3) (100-3)
=1002-32
=9 991 ;
(2)118×122
=(120-2) (100+2)
=1202-22
=14 396 .
关键:
a为两数和的平均数;
b为|两数差|的平均数
例3:计算:
(1)a2 (a+b)(a-b)+a2 b2
(2)(2x-5)(2x+5)-2x(2x-3)
解: (1)a2 (a+b)(a-b)+a2 b2
=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4
(2)(2x-5)(2x+5)-2x(2x-3)
=4x2-52-(4x2-6x)
=4x2-25-4x2+6x
=6x-25
不符合平方差公式运算条件的乘法,按乘法法则进行运算.
例题讲解
例4:公式的逆用
(1)(x+y)2-(x-y)2 (2)252-242
分析:逆用平方差公式可以使运算简便.
解:(1)(x+y)2-(x-y)2
=[(x+y)+(x-y)][(x+y)-(x-y)]
=2x·2y
=4xy
(2)252-242
=(25+24)(25-24)
=49
例题讲解
解:李大妈吃亏了.理由如下:原正方形的面积为a2,改变边长后面积为(a+4)(a-4)=a2-16.
∵a2>a2-16,
∴李大妈吃亏了.
例5. 王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
例题讲解
随堂练习
1. 将图甲中阴影部分的小长方形变换到图乙位置,根据两个图形的面积关系可以得到一个关于a,b的恒等式为( )
A.(a-b)2=a2-2ab+b2 B.(a+b)2=a2+2ab+b2
C.(a+b)(a-b)=a2-b2 D.a(a-b)=a2-ab
C
随堂练习
2.如图,在边长为a的正方形中裁掉一个边长为b的小正方形(如图1),将剩余部分沿虚线剪开后拼接(如图2),通过计算,用拼接前后两个图形中阴影部分的面积可以验证等式( )
A.a2-b2=(a+b)(a-b)
B.(a+b)2=a2+2ab+b2
C.(a+2b)(a-b)=a2+ab-2b2
D.(a-b)2=a2-2ab+b2
A
随堂练习
3.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的长方形.根据图形的变化过程写出的一个正确的等式是( )
A.a(a-b)=a2-ab
B.(a-b)2=a2-2ab+b2
C.(a-b)2=a2-b2
D.a2-b2=(a+b)(a-b)
D
随堂练习
4. 计算2 0162-2 015×2 017的结果是( )
A.1 B.-1
C.2 D.-2
A
5.(x+6)(x-6)-x(x-9)=0的解是______.
x=4
随堂练习
6.(1)如图①,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)若将阴影部分裁剪下来,重新拼成一个长方形,如图②,则这个长方形的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图①②中阴影部分的面积,
可以得到什么结论
a2-b2
a-b
a+b
(a+b)(a-b)
结论:(a+b)(a-b)=a2-b2.
随堂练习
7. 填空:
(1)已知(x-a)(x+a)=x2-9,则a的值为________;
(2)若(m+4x)(m-4x)=36-nx2,则mn的值为________.
±96
±3
8. 97×103=_______________=______________=
________________=_______________.
(100-3)(100+3)
1002-9
10000-9
9991
随堂练习
9. 请先观察下列算式,再填空:
32-12=8×1,52-32=8×2.
①72-52=8×______;
②92-(_____)2=8×4;
③(_____)2-92=8×5;
④132-(_____)2=8×______;
….
3
7
11
11
6
随堂练习
10.计算:
(1)102×98(用简便方法计算); (2)(x-1)(x+1)(x2+1).
解:原式=(100+2)(100-2)
=1002-22
=10 000-4
=9 996
解:原式=(x2-1)(x2+1)
=(x2)2-12
=x4-1
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
