河北省邯郸市涉县第二中学2013-2014学年高二3月月考数学(理)试题
文档属性
| 名称 | 河北省邯郸市涉县第二中学2013-2014学年高二3月月考数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 279.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-19 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
说明:
一、本试卷分为第Ⅰ卷和第Ⅱ卷.第Ⅰ卷为选择题;第Ⅱ卷为非选择题,分为必考和选考两部分.
二、答题前请仔细阅读答题卡上的“注意事项”,按照“注意事项”的规定答题.
三、做选择题时,每小题选出答案后,用铅笔把答题卡上对应题目的标号涂黑.如需改动,用橡皮将原选涂答案擦干净后,再选涂其他答案.
四、考试结束后,将本试卷与原答题卡一并交回.
第Ⅰ卷
1、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项符合题目要求.
(1)复数(1-)(1+i)=
(A)-2 (B)2 (C)-2i (D)2i
(2)函数y=的定义域为
(A)(0,8] (B)(2,8]
(C)(-2,8] (D)[8,+∞)
(3)已知a,b是两个不共线的单位向量,|a-b|=,则(2a-b)·(3a+b)=
(A) (B)-
(C) (D)-
(4)以(-4,0),(4,0)为焦点,y=±x为渐近线的双曲线的方程为
(A)-=1 (B)-=1
(C)-=1 (D)-=1
(5)执行右面的程序框图,则输出的S为
(A)-45 (B)36
(C)55 (D)-66
(6)设等比数列{an}的各项都为正数,a1+a2+…+a6=1,++…+=10,则a1a2…a6=
(A)103 (B)10-3
(C)106 (D)10-6
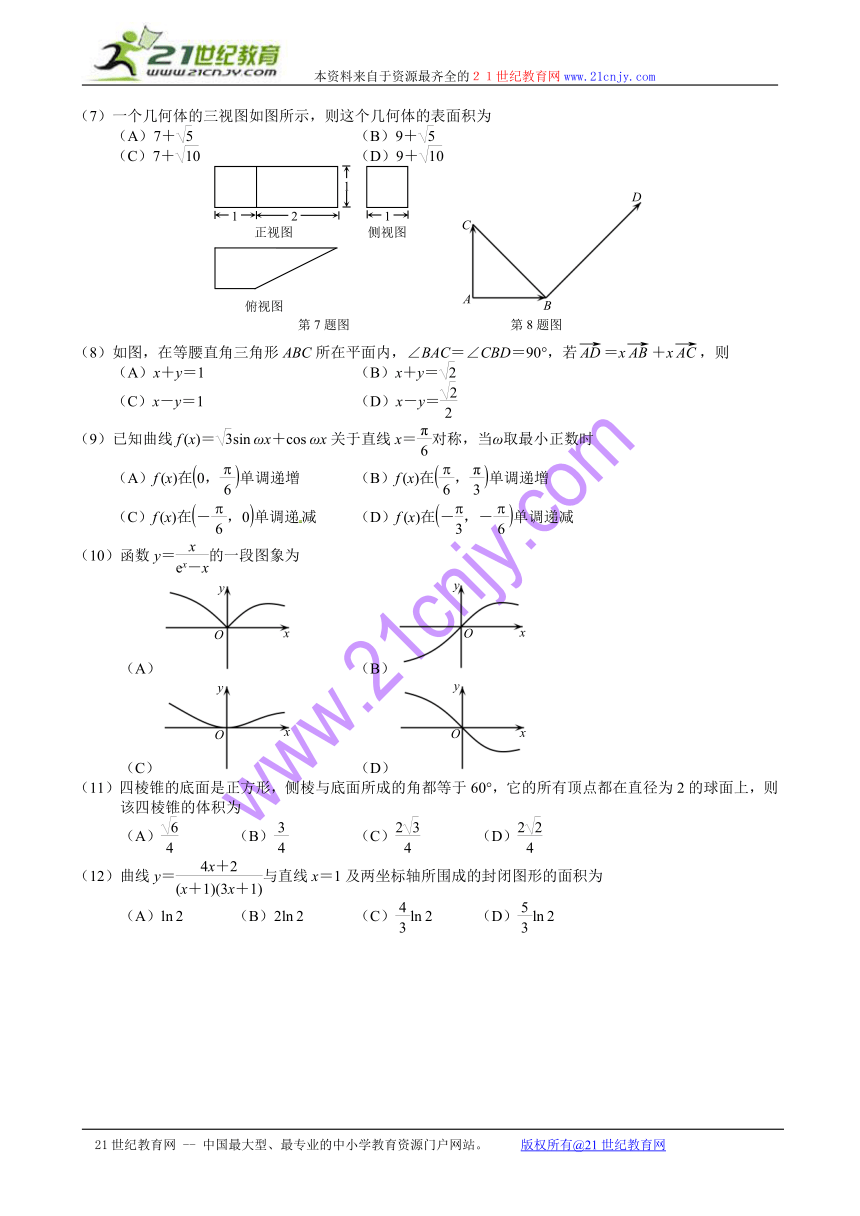
(7)一个几何体的三视图如图所示,则这个几何体的表面积为
(A)7+ (B)9+
(C)7+ (D)9+
第7题图 第8题图
(8)如图,在等腰直角三角形ABC所在平面内,∠BAC=∠CBD=90,若=x+x,则
(A)x+y=1 (B)x+y=
(C)x-y=1 (D)x-y=
(9)已知曲线f(x)=sinωx+cosωx关于直线x=对称,当ω取最小正数时
(A)f(x)在(0,)单调递增 (B)f(x)在(,)单调递增
(C)f(x)在(-,0)单调递减 (D)f(x)在(-,-)单调递减
(10)函数y=的一段图象为
(A) (B)
(C) (D)
(11)四棱锥的底面是正方形,侧棱与底面所成的角都等于60,它的所有顶点都在直径为2的球面上,则该四棱锥的体积为
(A) (B) (C) (D)
(12)曲线y=与直线x=1及两坐标轴所围成的封闭图形的面积为
(A)ln2 (B)2ln2 (C)ln2 (D)ln2
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.把答案填写在题中横线上.
(13)考古学家通过始祖鸟化石标本发现:其股骨长度x(cm)与肱骨长度y(cm)线性回归方程为=1.197x-3.660,由此估计,当股骨长度为50cm时,肱骨长度的估计值为___________cm.
(14)椭圆+=1(a>b>0))的左、右焦点分别为F1,F2,过F2作x轴的垂线与椭圆的一个交点为P,若∠F1PF2=45,则椭圆的离心率e=__________.
(15)若β=α+30,则化简sin2α+cos2β+sinαcosβ的结果为_________.
(16)在数列{an}中,a1=a7=1,|an+1-an|=1,Sn是数列{an}的前n项和,则S10的最大值等于__________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
(17)(本小题满分12分)
如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点.
(Ⅰ)若CP=CQ,且△CPQ的面积为,求∠BCP的大小;
(Ⅱ)若△APQ的周长为2,求∠PCQ的大小.
(18)(本小题满分12分)
如图,在四棱锥S—ABCD中,SD⊥底面ABCD,底面ABCD是矩形,且SD=AD=AB,E是SA的中点.
(Ⅰ)求证:平面BED⊥平面SAB;
(Ⅱ)求平面BED与平面SBC所成二面角(锐角)的大小.
(19)(本小题满分12分)
张师傅驾车从公司开往火车站,途经甲、乙、丙、丁4个交通岗,这4个交通岗将公司到火车站分成的5个时段,每个时段的驾车时间都是3分钟.甲、乙两交通岗遇到红灯的概率都是;丙、丁两交通岗遇到红灯的概率都是.每个交通岗遇到红灯都需要停车1分钟.假设他在各交通岗遇到红灯是相互独立的.
(Ⅰ)求张师傅此行程时间不小于16分钟的概率;
(Ⅱ)记张师傅此行程所需时间为X分钟,求X的分布列和均值.
(20)(本小题满分12分)
已知抛物线P:x2=4y(p>0)的焦点为F,过点F作直线l与P交于A,B两点,P的准线与y轴交于点C.
(Ⅰ)证明:直线CA与CB关于y轴对称;
(Ⅱ)当直线CB的倾斜角为45时,求△ABC内切圆的方程.
(21)(本小题满分12分)
已知函数f(x)=ax2-x+lnx(a>0).
(Ⅰ)若f(x)是单调函数,求a的取值范围;21世纪教育网
(Ⅱ)若f(x)有两个极值点x1,x2,证明:f(x1)+f(x2)<2ln2-3.
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,E是圆O内两弦AB和CD的交点,F是AD延长线上一点,FG与圆O相切于点G,且EF=FG.求证:
(Ⅰ)△EFD∽△AFE;
(Ⅱ)EF∥BC.
(23)(本小题满分10分)选修4-4:坐标系与参数方程
直角坐标系xOy和极坐标系Ox的原点与极点重合,x轴正半轴与极轴重合,单位长度相同.在直角坐标系下,曲线C的参数方程为(φ为参数).
(Ⅰ)在极坐标系下,曲线C与射线θ=和射线θ=-分别交于A,B两点,求△AOB的面积;
(Ⅱ)在直角坐标系下,直线l的参数方程为(t为参数),求曲线C与直线l的交点坐标.
(24)(本小题满分10分)选修4-5:不等式选讲
已知f(x)=|x+1|+|x-2|.
(Ⅰ)解不等式f(x)≤7;
(Ⅱ)若f(x)+f(-x)≥a,求a的取值范围.
理科数学参考答案
2、 选择题:
(1)D (2)C (3)C (4)A (5)C (6)B
(7)B (8)C (9)A (10)B (11)B (12)D
二、填空题:
(18)解:
(Ⅰ)因为SD⊥平面ABCD,所以平面SAD⊥平面ABCD,
因为AB⊥AD,所以AB⊥平面SAD,所以DE⊥AB.
因为SD=AD,E是SA的中点,所以DE⊥SA,
又AB∩SA=A,所以DE⊥平面SAB,
所以平面BED⊥平面SAB. …4分
(Ⅱ)建立如图所示的坐标系D—xyz,取AD=2,则
D(0,0,0),A(2,0,0),B(2,,0),
C(0,,0),S(0,0,2),E(1,0,1).
=(2, ,0),=(1,0,1),=(2,0,0),=(0,-,2).
设m=(x1,y1,z1)是面BED的一个法向量,则
即
因此可取m=(-1,,1). …8分
设n=(x2,y2,z2)是面SBC的一个法向量,则
即
因此可取n=(0,,1). …10分
cosm,n===,
故平面BED与平面SBC所成锐二面角的大小为30. …12分
(19)解:
(Ⅰ)如果不遇到红灯,全程需要15分钟,否则至少需要16分钟.
张师傅此行程时间不小于16分钟的概率
P=1-()2()2=. …4分
(Ⅱ)依题意,X的可能取值为15,16,17,18,19.
P(X=15)=()2()2==,
P(X=16)=C··()2+()2·C()2==,
P(X=17)=()2·()2+C··C()2+()2·()2=,
P(X=18)=()2·C()2+C··()2==,
P(X=19)=()2()2=.
X的分布列为
Y 15 16 17 18 19
P …10分
X的均值
E(X)=15×+16×+17×+18×+19×=. …12分
(20)解:
令g(a)=-1-ln(2a),a∈(0,],21世纪教育网
则当a∈(0,)时,g(a)=-=>0,g(a)在(0,]单调递增,
所以g(a)<g()=2ln2-3,即f(x1)+f(x2)<2ln2-3. …12分
(22)证明:
(Ⅰ)因为FG与圆O相切于点G,所以FG2=FD·FA.
因为EF=FG,EF2=FD·FA,所以=,
因为∠EFD=∠AFE,所以△EFD∽△AFE. …5分
(Ⅱ)由(Ⅰ),有∠FED=∠FAE,
因为∠FAE和∠BCD都是上的圆周角,所以∠FED=∠BCD,
因此EF∥BC. …10分
(24)解:
(Ⅰ)f(x)=
当x<-1时,由1-2x≤7,得-3≤x<-1;
当-1≤x≤-2时,有3≤7;
当x>2时,由2x-1≤7,得2<x≤4.
综上,不等式f(x)≤7的解集为[-3,4]. …5分
(Ⅱ)f(x)=|x+1|+|x-2|≥|(x+1)-(x-2)|=3,
当且仅当-1≤x≤2时等号成立;
同理f(-x)≥3,当且仅当-2≤x≤1时等号成立.21世纪教育网
所以f(x)+f(-x)≥6,当且仅当-1≤x≤1时等号成立.
故a的取值范围是(-∞,6].
开始
否
输出S
k>9
是
结束
k=0,S=0
k=k+1
a=(-1)kk2
S=S+a
侧视图
俯视图
1
2
1
正视图
1
A
B
C
D
x
y
O
x
O
y
x
y
O
x
O
y
A
C
B
D
Q
P
A
C
B
D
E
S
B
D
A
O
E
G
F
C
A
C
B
D
E
S
x
y
z
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
说明:
一、本试卷分为第Ⅰ卷和第Ⅱ卷.第Ⅰ卷为选择题;第Ⅱ卷为非选择题,分为必考和选考两部分.
二、答题前请仔细阅读答题卡上的“注意事项”,按照“注意事项”的规定答题.
三、做选择题时,每小题选出答案后,用铅笔把答题卡上对应题目的标号涂黑.如需改动,用橡皮将原选涂答案擦干净后,再选涂其他答案.
四、考试结束后,将本试卷与原答题卡一并交回.
第Ⅰ卷
1、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项符合题目要求.
(1)复数(1-)(1+i)=
(A)-2 (B)2 (C)-2i (D)2i
(2)函数y=的定义域为
(A)(0,8] (B)(2,8]
(C)(-2,8] (D)[8,+∞)
(3)已知a,b是两个不共线的单位向量,|a-b|=,则(2a-b)·(3a+b)=
(A) (B)-
(C) (D)-
(4)以(-4,0),(4,0)为焦点,y=±x为渐近线的双曲线的方程为
(A)-=1 (B)-=1
(C)-=1 (D)-=1
(5)执行右面的程序框图,则输出的S为
(A)-45 (B)36
(C)55 (D)-66
(6)设等比数列{an}的各项都为正数,a1+a2+…+a6=1,++…+=10,则a1a2…a6=
(A)103 (B)10-3
(C)106 (D)10-6
(7)一个几何体的三视图如图所示,则这个几何体的表面积为
(A)7+ (B)9+
(C)7+ (D)9+
第7题图 第8题图
(8)如图,在等腰直角三角形ABC所在平面内,∠BAC=∠CBD=90,若=x+x,则
(A)x+y=1 (B)x+y=
(C)x-y=1 (D)x-y=
(9)已知曲线f(x)=sinωx+cosωx关于直线x=对称,当ω取最小正数时
(A)f(x)在(0,)单调递增 (B)f(x)在(,)单调递增
(C)f(x)在(-,0)单调递减 (D)f(x)在(-,-)单调递减
(10)函数y=的一段图象为
(A) (B)
(C) (D)
(11)四棱锥的底面是正方形,侧棱与底面所成的角都等于60,它的所有顶点都在直径为2的球面上,则该四棱锥的体积为
(A) (B) (C) (D)
(12)曲线y=与直线x=1及两坐标轴所围成的封闭图形的面积为
(A)ln2 (B)2ln2 (C)ln2 (D)ln2
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.把答案填写在题中横线上.
(13)考古学家通过始祖鸟化石标本发现:其股骨长度x(cm)与肱骨长度y(cm)线性回归方程为=1.197x-3.660,由此估计,当股骨长度为50cm时,肱骨长度的估计值为___________cm.
(14)椭圆+=1(a>b>0))的左、右焦点分别为F1,F2,过F2作x轴的垂线与椭圆的一个交点为P,若∠F1PF2=45,则椭圆的离心率e=__________.
(15)若β=α+30,则化简sin2α+cos2β+sinαcosβ的结果为_________.
(16)在数列{an}中,a1=a7=1,|an+1-an|=1,Sn是数列{an}的前n项和,则S10的最大值等于__________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
(17)(本小题满分12分)
如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点.
(Ⅰ)若CP=CQ,且△CPQ的面积为,求∠BCP的大小;
(Ⅱ)若△APQ的周长为2,求∠PCQ的大小.
(18)(本小题满分12分)
如图,在四棱锥S—ABCD中,SD⊥底面ABCD,底面ABCD是矩形,且SD=AD=AB,E是SA的中点.
(Ⅰ)求证:平面BED⊥平面SAB;
(Ⅱ)求平面BED与平面SBC所成二面角(锐角)的大小.
(19)(本小题满分12分)
张师傅驾车从公司开往火车站,途经甲、乙、丙、丁4个交通岗,这4个交通岗将公司到火车站分成的5个时段,每个时段的驾车时间都是3分钟.甲、乙两交通岗遇到红灯的概率都是;丙、丁两交通岗遇到红灯的概率都是.每个交通岗遇到红灯都需要停车1分钟.假设他在各交通岗遇到红灯是相互独立的.
(Ⅰ)求张师傅此行程时间不小于16分钟的概率;
(Ⅱ)记张师傅此行程所需时间为X分钟,求X的分布列和均值.
(20)(本小题满分12分)
已知抛物线P:x2=4y(p>0)的焦点为F,过点F作直线l与P交于A,B两点,P的准线与y轴交于点C.
(Ⅰ)证明:直线CA与CB关于y轴对称;
(Ⅱ)当直线CB的倾斜角为45时,求△ABC内切圆的方程.
(21)(本小题满分12分)
已知函数f(x)=ax2-x+lnx(a>0).
(Ⅰ)若f(x)是单调函数,求a的取值范围;21世纪教育网
(Ⅱ)若f(x)有两个极值点x1,x2,证明:f(x1)+f(x2)<2ln2-3.
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,E是圆O内两弦AB和CD的交点,F是AD延长线上一点,FG与圆O相切于点G,且EF=FG.求证:
(Ⅰ)△EFD∽△AFE;
(Ⅱ)EF∥BC.
(23)(本小题满分10分)选修4-4:坐标系与参数方程
直角坐标系xOy和极坐标系Ox的原点与极点重合,x轴正半轴与极轴重合,单位长度相同.在直角坐标系下,曲线C的参数方程为(φ为参数).
(Ⅰ)在极坐标系下,曲线C与射线θ=和射线θ=-分别交于A,B两点,求△AOB的面积;
(Ⅱ)在直角坐标系下,直线l的参数方程为(t为参数),求曲线C与直线l的交点坐标.
(24)(本小题满分10分)选修4-5:不等式选讲
已知f(x)=|x+1|+|x-2|.
(Ⅰ)解不等式f(x)≤7;
(Ⅱ)若f(x)+f(-x)≥a,求a的取值范围.
理科数学参考答案
2、 选择题:
(1)D (2)C (3)C (4)A (5)C (6)B
(7)B (8)C (9)A (10)B (11)B (12)D
二、填空题:
(18)解:
(Ⅰ)因为SD⊥平面ABCD,所以平面SAD⊥平面ABCD,
因为AB⊥AD,所以AB⊥平面SAD,所以DE⊥AB.
因为SD=AD,E是SA的中点,所以DE⊥SA,
又AB∩SA=A,所以DE⊥平面SAB,
所以平面BED⊥平面SAB. …4分
(Ⅱ)建立如图所示的坐标系D—xyz,取AD=2,则
D(0,0,0),A(2,0,0),B(2,,0),
C(0,,0),S(0,0,2),E(1,0,1).
=(2, ,0),=(1,0,1),=(2,0,0),=(0,-,2).
设m=(x1,y1,z1)是面BED的一个法向量,则
即
因此可取m=(-1,,1). …8分
设n=(x2,y2,z2)是面SBC的一个法向量,则
即
因此可取n=(0,,1). …10分
cosm,n===,
故平面BED与平面SBC所成锐二面角的大小为30. …12分
(19)解:
(Ⅰ)如果不遇到红灯,全程需要15分钟,否则至少需要16分钟.
张师傅此行程时间不小于16分钟的概率
P=1-()2()2=. …4分
(Ⅱ)依题意,X的可能取值为15,16,17,18,19.
P(X=15)=()2()2==,
P(X=16)=C··()2+()2·C()2==,
P(X=17)=()2·()2+C··C()2+()2·()2=,
P(X=18)=()2·C()2+C··()2==,
P(X=19)=()2()2=.
X的分布列为
Y 15 16 17 18 19
P …10分
X的均值
E(X)=15×+16×+17×+18×+19×=. …12分
(20)解:
令g(a)=-1-ln(2a),a∈(0,],21世纪教育网
则当a∈(0,)时,g(a)=-=>0,g(a)在(0,]单调递增,
所以g(a)<g()=2ln2-3,即f(x1)+f(x2)<2ln2-3. …12分
(22)证明:
(Ⅰ)因为FG与圆O相切于点G,所以FG2=FD·FA.
因为EF=FG,EF2=FD·FA,所以=,
因为∠EFD=∠AFE,所以△EFD∽△AFE. …5分
(Ⅱ)由(Ⅰ),有∠FED=∠FAE,
因为∠FAE和∠BCD都是上的圆周角,所以∠FED=∠BCD,
因此EF∥BC. …10分
(24)解:
(Ⅰ)f(x)=
当x<-1时,由1-2x≤7,得-3≤x<-1;
当-1≤x≤-2时,有3≤7;
当x>2时,由2x-1≤7,得2<x≤4.
综上,不等式f(x)≤7的解集为[-3,4]. …5分
(Ⅱ)f(x)=|x+1|+|x-2|≥|(x+1)-(x-2)|=3,
当且仅当-1≤x≤2时等号成立;
同理f(-x)≥3,当且仅当-2≤x≤1时等号成立.21世纪教育网
所以f(x)+f(-x)≥6,当且仅当-1≤x≤1时等号成立.
故a的取值范围是(-∞,6].
开始
否
输出S
k>9
是
结束
k=0,S=0
k=k+1
a=(-1)kk2
S=S+a
侧视图
俯视图
1
2
1
正视图
1
A
B
C
D
x
y
O
x
O
y
x
y
O
x
O
y
A
C
B
D
Q
P
A
C
B
D
E
S
B
D
A
O
E
G
F
C
A
C
B
D
E
S
x
y
z
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
