5.1.1 变化率问题课件-2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册(共32张PPT)
文档属性
| 名称 | 5.1.1 变化率问题课件-2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 891.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 08:00:13 | ||
图片预览











文档简介
(共32张PPT)
5.1.1 变化率问题
第五章
内容索引
01
02
基础落实·必备知识全过关
重难探究·能力素养全提升
03
学以致用·随堂检测全达标
课标要求
1.理解平均速度和瞬时速度的关系,并能求解平均速度和瞬时速度.
2.体会抛物线上割线与切线的关系,能求解抛物线上某点处的切线斜率.
基础落实·必备知识全过关
知识点1 平均速度与瞬时速度
1.平均速度:物体的位移与所用时间的比值,通常指物体在某一时间段的速度.
若物体运动的位移与时间的关系式是s=f(t),函数f(t)在t0与t0+Δt之间的平均速度是
2.瞬时速度:在物理中,做变速运动的物体在不同的时刻,速度是不同的,我们把物体在某一时刻的速度称为瞬时速度.
变速运动物体在不同时刻瞬时速度不同
名师点睛 从物理的角度看,瞬时速度就是将平均速度的时间段改为时间点,即让时间段[t,t+Δt](Δt>0)或者[t+Δt,t](Δt<0)中的时间间隔|Δt|无限趋近于0,此时时间段[t,t+Δt](Δt>0)或者[t+Δt,t](Δt<0)内的平均速度就无限趋近于t时刻的瞬时速度.
名师点睛
从物理的角度看,瞬时速度就是将平均速度的时间段改为时间点,即让时间段[t,t+Δt](Δt>0)或者[t+Δt,t](Δt<0)中的时间间隔|Δt|无限趋近于0,此时时间段[t,t+Δt](Δt>0)或者[t+Δt,t](Δt<0)内的平均速度就无限趋近于t时刻的瞬时速度.
过关自诊
1.判断正误.(正确的打√,错误的打×)
(1)圆的半径r从0.1变化到0.3时,圆的面积S的平均变化率为0.4π.( )
(2)已知某质点的运动路程s(单位:m)与时间t(单位:s)的关系为s(t)=5t2,则在1 s到3 s这段时间内,该质点的平均速度为20 m/s.( )
(3)汽车在行驶时的平均速度与瞬时速度一定不相等.( )
(4)平均速度刻画运动物体在某一时间段内变化的快慢程度,瞬时速度刻画物体在某一时刻变化的快慢程度.( )
√
√
×
√
2.平均速度与瞬时速度有什么不同
提示 平均速度表示的是运动的物体在某一段时间内的快慢程度.瞬时速度反映的是物体在运动过程的某一时刻的运动情况,能精确表示任一时刻物体运动的快慢和方向.
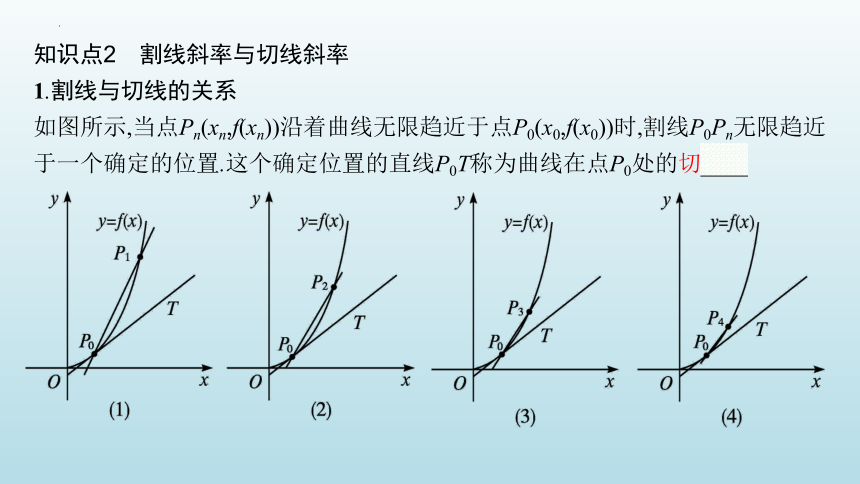
知识点2 割线斜率与切线斜率
1.割线与切线的关系
如图所示,当点Pn(xn,f(xn))沿着曲线无限趋近于点P0(x0,f(x0))时,割线P0Pn无限趋近于一个确定的位置.这个确定位置的直线P0T称为曲线在点P0处的切线.
2.割线斜率与切线斜率的关系
f(x0+Δx)-f(x0)可记为Δy,并且Δy可为正数,可为负数,可为零
过关自诊
1.判断正误.(正确的打√,错误的打×)
(1)曲线上给定一点P,过点P可以作该曲线的无数条割线.( )
(2)有的曲线过它上面的某一点可作两条切线.( )
(3)抛物线上的任意一点处都存在过该点的切线.( )
(4)“过点P的曲线y=f(x)的切线”与“曲线y=f(x)在点P处的切线”这两句话含意相同.( )
√
×
√
×
2.如图,我们把一条曲线上的任意一点P附近的图象不断放大,观察有何现象出现
提示 平均速度表示的是运动的物体在某一段时间内的快慢程度.瞬时速度反映的是物体在运动过程的某一时刻的运动情况,能精确表示任一时刻物体运动的快慢和方向.
重难探究·能力素养全提升
探究点一
求物体运动的平均速度及瞬时速度
角度1 平均速度
【例1】某质点运动的方程为f(x)=-2x2+1(x表示时间,f(x)表示位移),则该质点从x=1到x=2的平均速度为( )
A.-4 B.-8 C.6 D.-6
答案 D
解析 由题得该质点从x=1到x=2的平均速度为
故选D.
规律方法 求物体运动的平均速度的三个步骤
第一步:求时间的改变量x2-x1;
第二步:求位移的改变量f(x2)-f(x1);
变式训练 1质点的运动规律为s=t2+3(t表示时间,s表示位移),则在时间[3,3+Δt]中,质点的平均速度等于( )
A.6+Δt B.6+Δt+
C.3+Δt D.9+Δt
答案 A
解析 平均速度为
角度2 瞬时速度
【例2】某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,求物体在t=1 s时的瞬时速度.
变式探究 1在本例条件不变的前提下,试求物体的初速度.
变式探究 2在本例条件不变的前提下,试问物体在哪一时刻的瞬时速度为9 m/s.
规律方法 求运动物体在t=t0时的瞬时速度的三个步骤
(1)求时间改变量Δt和位移改变量s(t0+Δt)-s(t0).
探究点二
求解曲线在某点处的割线、切线斜率
【例3】设函数f(x)=x(x-6),则此函数图象在x=0处的切线斜率为( )
A.0 B.-1 C.3 D.-6
答案 D
规律方法 求曲线上某点(x0,f(x0))处的割线或切线斜率的步骤
答案 A
本节要点归纳
1.知识清单:
(1)平均速度与瞬时速度的概念和计算.
(2)曲线的割线与切线及其求解.
2.方法归纳:局部以直代曲法,极限的无限逼近
思想,数形结合思想.
3.常见误区:(1)不会用极限的思想理解瞬时速度;(2)容易忽视函数平均变化率的符号.
学以致用·随堂检测全达标
1.若一质点的运动方程为s=t2+1,则在时间段[1,2]中的平均速度是( )
A.2 B.3 C.4 D.5
答案 B
2.已知一直线运动的物体,当时间从t变到t+Δt时,物体的位移为Δs,那么
A.时间从t变到t+Δt时物体的速度
B.在t时刻该物体的瞬时速度
C.当时间为Δt时物体的速度
D.时间从t变到t+Δt时物体的平均速度
答案 B
3.某运动物体的位移s(单位:米)关于时间t(单位:秒)的函数关系式为s=2t+1,则该物体在t=1秒时的瞬时速度为( )
A.1米/秒 B.2米/秒
C.3米/秒 D.4米/秒
答案 B
4.过曲线f(x)=x2+1上两点P(1,2)和Q(1+Δx,2+Δy)作曲线的割线,当Δx=0.1时,割线的斜率k= ;当Δx=0.001时,割线的斜率k= .
答案 2.1 2.001
解析 若Δx=0.1,则1+Δx=1.1,
则f(1.1)=1.12+1=1.21+1=2.21,
若Δx=0.001,则1+Δx=1.001,
则f(1.001)=1.0012+1=2.002 001,
5.曲线f(x)=x2-2x+1在x=4处切线的斜率为 .
答案 6
谢 谢 观 看
5.1.1 变化率问题
第五章
内容索引
01
02
基础落实·必备知识全过关
重难探究·能力素养全提升
03
学以致用·随堂检测全达标
课标要求
1.理解平均速度和瞬时速度的关系,并能求解平均速度和瞬时速度.
2.体会抛物线上割线与切线的关系,能求解抛物线上某点处的切线斜率.
基础落实·必备知识全过关
知识点1 平均速度与瞬时速度
1.平均速度:物体的位移与所用时间的比值,通常指物体在某一时间段的速度.
若物体运动的位移与时间的关系式是s=f(t),函数f(t)在t0与t0+Δt之间的平均速度是
2.瞬时速度:在物理中,做变速运动的物体在不同的时刻,速度是不同的,我们把物体在某一时刻的速度称为瞬时速度.
变速运动物体在不同时刻瞬时速度不同
名师点睛 从物理的角度看,瞬时速度就是将平均速度的时间段改为时间点,即让时间段[t,t+Δt](Δt>0)或者[t+Δt,t](Δt<0)中的时间间隔|Δt|无限趋近于0,此时时间段[t,t+Δt](Δt>0)或者[t+Δt,t](Δt<0)内的平均速度就无限趋近于t时刻的瞬时速度.
名师点睛
从物理的角度看,瞬时速度就是将平均速度的时间段改为时间点,即让时间段[t,t+Δt](Δt>0)或者[t+Δt,t](Δt<0)中的时间间隔|Δt|无限趋近于0,此时时间段[t,t+Δt](Δt>0)或者[t+Δt,t](Δt<0)内的平均速度就无限趋近于t时刻的瞬时速度.
过关自诊
1.判断正误.(正确的打√,错误的打×)
(1)圆的半径r从0.1变化到0.3时,圆的面积S的平均变化率为0.4π.( )
(2)已知某质点的运动路程s(单位:m)与时间t(单位:s)的关系为s(t)=5t2,则在1 s到3 s这段时间内,该质点的平均速度为20 m/s.( )
(3)汽车在行驶时的平均速度与瞬时速度一定不相等.( )
(4)平均速度刻画运动物体在某一时间段内变化的快慢程度,瞬时速度刻画物体在某一时刻变化的快慢程度.( )
√
√
×
√
2.平均速度与瞬时速度有什么不同
提示 平均速度表示的是运动的物体在某一段时间内的快慢程度.瞬时速度反映的是物体在运动过程的某一时刻的运动情况,能精确表示任一时刻物体运动的快慢和方向.
知识点2 割线斜率与切线斜率
1.割线与切线的关系
如图所示,当点Pn(xn,f(xn))沿着曲线无限趋近于点P0(x0,f(x0))时,割线P0Pn无限趋近于一个确定的位置.这个确定位置的直线P0T称为曲线在点P0处的切线.
2.割线斜率与切线斜率的关系
f(x0+Δx)-f(x0)可记为Δy,并且Δy可为正数,可为负数,可为零
过关自诊
1.判断正误.(正确的打√,错误的打×)
(1)曲线上给定一点P,过点P可以作该曲线的无数条割线.( )
(2)有的曲线过它上面的某一点可作两条切线.( )
(3)抛物线上的任意一点处都存在过该点的切线.( )
(4)“过点P的曲线y=f(x)的切线”与“曲线y=f(x)在点P处的切线”这两句话含意相同.( )
√
×
√
×
2.如图,我们把一条曲线上的任意一点P附近的图象不断放大,观察有何现象出现
提示 平均速度表示的是运动的物体在某一段时间内的快慢程度.瞬时速度反映的是物体在运动过程的某一时刻的运动情况,能精确表示任一时刻物体运动的快慢和方向.
重难探究·能力素养全提升
探究点一
求物体运动的平均速度及瞬时速度
角度1 平均速度
【例1】某质点运动的方程为f(x)=-2x2+1(x表示时间,f(x)表示位移),则该质点从x=1到x=2的平均速度为( )
A.-4 B.-8 C.6 D.-6
答案 D
解析 由题得该质点从x=1到x=2的平均速度为
故选D.
规律方法 求物体运动的平均速度的三个步骤
第一步:求时间的改变量x2-x1;
第二步:求位移的改变量f(x2)-f(x1);
变式训练 1质点的运动规律为s=t2+3(t表示时间,s表示位移),则在时间[3,3+Δt]中,质点的平均速度等于( )
A.6+Δt B.6+Δt+
C.3+Δt D.9+Δt
答案 A
解析 平均速度为
角度2 瞬时速度
【例2】某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,求物体在t=1 s时的瞬时速度.
变式探究 1在本例条件不变的前提下,试求物体的初速度.
变式探究 2在本例条件不变的前提下,试问物体在哪一时刻的瞬时速度为9 m/s.
规律方法 求运动物体在t=t0时的瞬时速度的三个步骤
(1)求时间改变量Δt和位移改变量s(t0+Δt)-s(t0).
探究点二
求解曲线在某点处的割线、切线斜率
【例3】设函数f(x)=x(x-6),则此函数图象在x=0处的切线斜率为( )
A.0 B.-1 C.3 D.-6
答案 D
规律方法 求曲线上某点(x0,f(x0))处的割线或切线斜率的步骤
答案 A
本节要点归纳
1.知识清单:
(1)平均速度与瞬时速度的概念和计算.
(2)曲线的割线与切线及其求解.
2.方法归纳:局部以直代曲法,极限的无限逼近
思想,数形结合思想.
3.常见误区:(1)不会用极限的思想理解瞬时速度;(2)容易忽视函数平均变化率的符号.
学以致用·随堂检测全达标
1.若一质点的运动方程为s=t2+1,则在时间段[1,2]中的平均速度是( )
A.2 B.3 C.4 D.5
答案 B
2.已知一直线运动的物体,当时间从t变到t+Δt时,物体的位移为Δs,那么
A.时间从t变到t+Δt时物体的速度
B.在t时刻该物体的瞬时速度
C.当时间为Δt时物体的速度
D.时间从t变到t+Δt时物体的平均速度
答案 B
3.某运动物体的位移s(单位:米)关于时间t(单位:秒)的函数关系式为s=2t+1,则该物体在t=1秒时的瞬时速度为( )
A.1米/秒 B.2米/秒
C.3米/秒 D.4米/秒
答案 B
4.过曲线f(x)=x2+1上两点P(1,2)和Q(1+Δx,2+Δy)作曲线的割线,当Δx=0.1时,割线的斜率k= ;当Δx=0.001时,割线的斜率k= .
答案 2.1 2.001
解析 若Δx=0.1,则1+Δx=1.1,
则f(1.1)=1.12+1=1.21+1=2.21,
若Δx=0.001,则1+Δx=1.001,
则f(1.001)=1.0012+1=2.002 001,
5.曲线f(x)=x2-2x+1在x=4处切线的斜率为 .
答案 6
谢 谢 观 看
