6.2.1向量的加法运算 课件-2022-2023学年高一下学期数学人教A版(2019)必修第二册(共41张PPT)
文档属性
| 名称 | 6.2.1向量的加法运算 课件-2022-2023学年高一下学期数学人教A版(2019)必修第二册(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 08:09:42 | ||
图片预览







文档简介
(共41张PPT)
定义: 既有大小又有方向的量
1.模(长度)
表示
有向线段
字母表示
零向量
单位向量
3.向量间的关系
相等
平行(共线)
向量
向量的有关概念
2.特殊向量
复习回顾
相反
作业讲评
O
N
M
M
O
N
重合
3.判断下列结论是否正确(正确的在括号内打“√”,错的打“×”),
并说明理由.
×
√
×
×
√
√
A
B
C
D
M
N
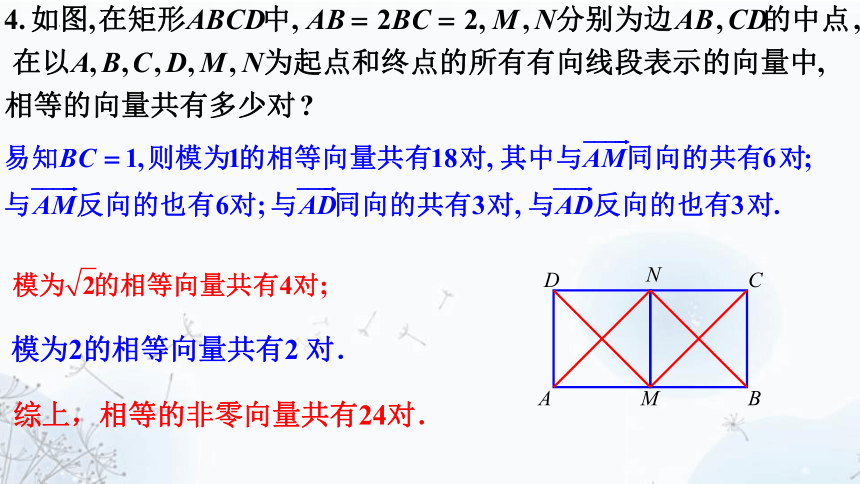
模为2的相等向量共有2 对.
综上,相等的非零向量共有24对.
6.2 向量的运算
6.2.1 向量的加法运算
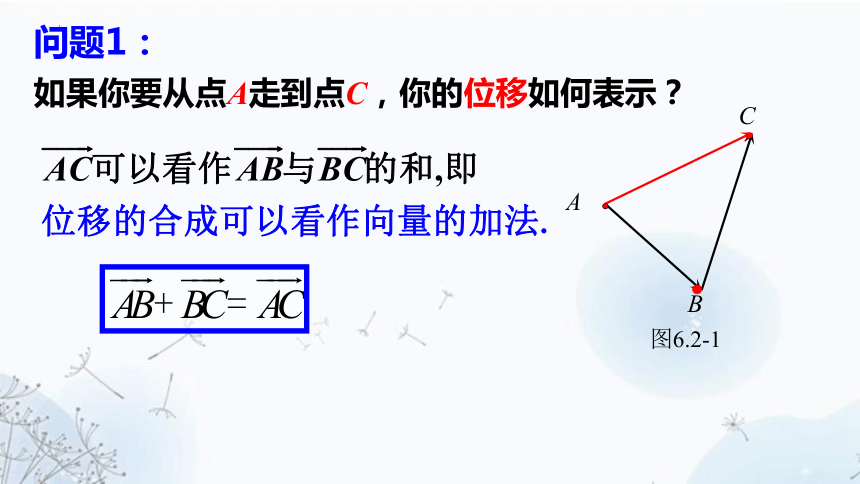
问题1:
如果你要从点A走到点C,你的位移如何表示?
A
C
B
图6.2-1
A
B
C
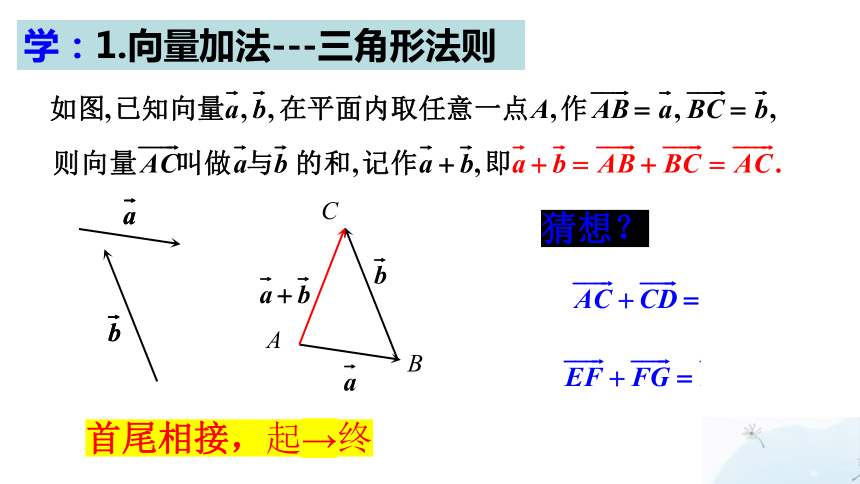
学:1.向量加法---三角形法则
首尾相接,起→终
猜想?
A
B
C
D
E
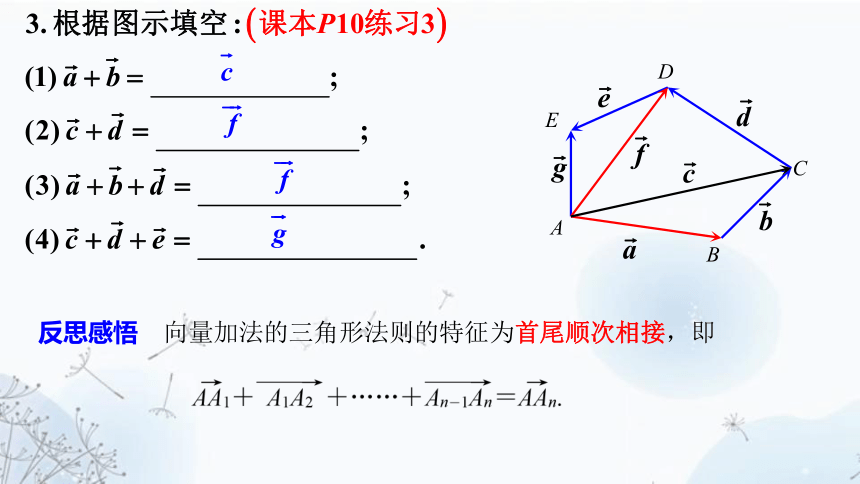
反思感悟 向量加法的三角形法则的特征为首尾顺次相接,即
问题2:
如图,一个物体受到F1与F2的作用,则该物体所受合力怎么求?
从运算的角度看,F可以看作是F1与F2的和,
即力的合成可以看作向量的加法.
C
O
A
B
C
学:2.向量加法---平行四边形形法则
起点相同,对角为和
例1 如图所示,
(1)a+b=____;
(2)c+d=___;
(3)a+b+d=___;
(4)c+d+e=___.
c
f
f
g
作业:步步高P3
点O是平行四边形ABCD的两条对角线的交点,则
等于
跟踪训练1
√
例2 (1)如图①所示,求作向量a+b;
如图③所示.
作业:步步高P4
(2)如图②所示,求作向量a+b+c.
解 方法一 (三角形法则)如图④所示,
方法二 (平行四边形法则)如图⑤所示,
以OA,OB为邻边作 OADB,连接OD,
再以OD,OC为邻边作 ODEC,连接OE,
如图所示,O为正六边形ABCDEF的中心,化简下列向量.
跟踪训练2
0
O
a
b
a + b
C
B
b
O
a
b
a + b
B
A
C
三 角 形 法 则:
平行四边形法则:
一致。平行四边形法则中利用了相等向量的平移。
问题3:向量加法的平行四边形法则与三角形法则的结果一致吗?
(1)
(2)
O
A
B
B
A
O
C
反思感悟 向量加法的平行四边形法则和三角形法则的区别和联系
区别 联系
三角形法则 (1)首尾相接 (2)适用于任何两个非零向量求和 当两个向量不共线时,三角形法则作出的图形是平行四边形法则作出图形的一半
平行四边形法则 (1)共起点 (2)仅适用于不共线的两个向量求和 跟踪训练1 如图所示,O为正六边形ABCDEF的中心,化简下列向量.
A
B
C
(1) 同向
(2)反向
A
B
C
1、不共线
o·
A
B
2、 共线
(1)同向
(2)反向
B
C
D
A
B
C
D
A
结论
探究2:
数的加法满足交换律、结合律,向量的加法是否也满足交换律和
结合律呢?
四、向量的加法运算律
例3 化简:
四、向量的加法运算律
四、向量的加法运算律
例2 长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图6.2-8,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15 km/h,同时江水的速度为向东6 km/h.
(1)用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度间的夹角表示,精确到1°).
A
B
C
D
图6.2-9
v水+v船=v实际
A
B
C
D
图6.2-9
(2)求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度间的夹角表示,精确到1°).
因此,船实际航行速度的大小约为16.2 km/h,方向与江水速度间的夹角约为68°.
河水自西向东流动的速度为10 km/h,小船在静水中的速度为
km/h,小船自南岸沿正北方向航行,求小船的实际航行速度.
例4
作业:步步高P5
v水+v船=v实际
设a,b分别表示水流的速度和小船在静水中的速度,
以OA,OB为邻边作矩形OACB,连接OC,如图,
∴∠AOC=60°,
∴小船的实际航行速度为20 km/h,沿北偏东30°的方向航行.
延伸探究 在静水中船的速度为20 m/min,水流的速度为10 m/min,如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向.
作出图形,如图所示.
船速v船与岸的方向成角α,由图可知v水+v船=v实际,结合已知条件,
四边形ABCD为平行四边形,
从而船与水流方向成120°的角.
所以船是沿与水流的方向成120°角的方向行进.
五、课堂小结
1、向量加法的三角形法则.
2、向量加法的平行四边形法则.
3、向量三角不等式.
4、向量加法的运算律.
常见误区:向量加法的三角形法则要注意向量首尾相接,
平行四边形法则要注意把向量移到共同起点.
随堂演练
解析 根据平面向量的加法运算,得
√
1
2
3
4
解析 在正方形ABCD中,AB=1,
√
1
2
3
4
3.(多选)下列等式不正确的是
A.a+(b+c)=(a+c)+b
1
2
3
4
D.|a+b|=|a|+|b|
√
√
D错误,当a,b方向相同时成立,故选B,D.
1
2
3
4
√
定义: 既有大小又有方向的量
1.模(长度)
表示
有向线段
字母表示
零向量
单位向量
3.向量间的关系
相等
平行(共线)
向量
向量的有关概念
2.特殊向量
复习回顾
相反
作业讲评
O
N
M
M
O
N
重合
3.判断下列结论是否正确(正确的在括号内打“√”,错的打“×”),
并说明理由.
×
√
×
×
√
√
A
B
C
D
M
N
模为2的相等向量共有2 对.
综上,相等的非零向量共有24对.
6.2 向量的运算
6.2.1 向量的加法运算
问题1:
如果你要从点A走到点C,你的位移如何表示?
A
C
B
图6.2-1
A
B
C
学:1.向量加法---三角形法则
首尾相接,起→终
猜想?
A
B
C
D
E
反思感悟 向量加法的三角形法则的特征为首尾顺次相接,即
问题2:
如图,一个物体受到F1与F2的作用,则该物体所受合力怎么求?
从运算的角度看,F可以看作是F1与F2的和,
即力的合成可以看作向量的加法.
C
O
A
B
C
学:2.向量加法---平行四边形形法则
起点相同,对角为和
例1 如图所示,
(1)a+b=____;
(2)c+d=___;
(3)a+b+d=___;
(4)c+d+e=___.
c
f
f
g
作业:步步高P3
点O是平行四边形ABCD的两条对角线的交点,则
等于
跟踪训练1
√
例2 (1)如图①所示,求作向量a+b;
如图③所示.
作业:步步高P4
(2)如图②所示,求作向量a+b+c.
解 方法一 (三角形法则)如图④所示,
方法二 (平行四边形法则)如图⑤所示,
以OA,OB为邻边作 OADB,连接OD,
再以OD,OC为邻边作 ODEC,连接OE,
如图所示,O为正六边形ABCDEF的中心,化简下列向量.
跟踪训练2
0
O
a
b
a + b
C
B
b
O
a
b
a + b
B
A
C
三 角 形 法 则:
平行四边形法则:
一致。平行四边形法则中利用了相等向量的平移。
问题3:向量加法的平行四边形法则与三角形法则的结果一致吗?
(1)
(2)
O
A
B
B
A
O
C
反思感悟 向量加法的平行四边形法则和三角形法则的区别和联系
区别 联系
三角形法则 (1)首尾相接 (2)适用于任何两个非零向量求和 当两个向量不共线时,三角形法则作出的图形是平行四边形法则作出图形的一半
平行四边形法则 (1)共起点 (2)仅适用于不共线的两个向量求和 跟踪训练1 如图所示,O为正六边形ABCDEF的中心,化简下列向量.
A
B
C
(1) 同向
(2)反向
A
B
C
1、不共线
o·
A
B
2、 共线
(1)同向
(2)反向
B
C
D
A
B
C
D
A
结论
探究2:
数的加法满足交换律、结合律,向量的加法是否也满足交换律和
结合律呢?
四、向量的加法运算律
例3 化简:
四、向量的加法运算律
四、向量的加法运算律
例2 长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图6.2-8,一艘船从长江南岸A地出发,垂直于对岸航行,航行速度的大小为15 km/h,同时江水的速度为向东6 km/h.
(1)用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度间的夹角表示,精确到1°).
A
B
C
D
图6.2-9
v水+v船=v实际
A
B
C
D
图6.2-9
(2)求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度间的夹角表示,精确到1°).
因此,船实际航行速度的大小约为16.2 km/h,方向与江水速度间的夹角约为68°.
河水自西向东流动的速度为10 km/h,小船在静水中的速度为
km/h,小船自南岸沿正北方向航行,求小船的实际航行速度.
例4
作业:步步高P5
v水+v船=v实际
设a,b分别表示水流的速度和小船在静水中的速度,
以OA,OB为邻边作矩形OACB,连接OC,如图,
∴∠AOC=60°,
∴小船的实际航行速度为20 km/h,沿北偏东30°的方向航行.
延伸探究 在静水中船的速度为20 m/min,水流的速度为10 m/min,如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向.
作出图形,如图所示.
船速v船与岸的方向成角α,由图可知v水+v船=v实际,结合已知条件,
四边形ABCD为平行四边形,
从而船与水流方向成120°的角.
所以船是沿与水流的方向成120°角的方向行进.
五、课堂小结
1、向量加法的三角形法则.
2、向量加法的平行四边形法则.
3、向量三角不等式.
4、向量加法的运算律.
常见误区:向量加法的三角形法则要注意向量首尾相接,
平行四边形法则要注意把向量移到共同起点.
随堂演练
解析 根据平面向量的加法运算,得
√
1
2
3
4
解析 在正方形ABCD中,AB=1,
√
1
2
3
4
3.(多选)下列等式不正确的是
A.a+(b+c)=(a+c)+b
1
2
3
4
D.|a+b|=|a|+|b|
√
√
D错误,当a,b方向相同时成立,故选B,D.
1
2
3
4
√
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
