18.1.2 第1课时 平行四边形的判定(1) 教案
文档属性
| 名称 | 18.1.2 第1课时 平行四边形的判定(1) 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 14:17:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
18.1.2平行四边形的判定
第1课时 平行四边形的判定1
核心素养目标:
1.在探索平行四边形的判别条件中,理解并掌握用边、对角线来判定平行四边形的方法.
2.会综合运用平行四边形的判定方法和性质来解决问题.
3.培养用类比、逆向联想及运动的思维方法来研究问题.
教学重难点:
重点:平行四边形的判定方法及应用.
难点:平行四边形的判定定理与性质定理的灵活应用.
教学过程:
问题导入
学行四边形之后,小明回家用细木棒钉制了一个平行四边形.第二天,小明拿着自己动手做的平行四边形向同学们展示.
小辉却问:你凭什么确定这四边形就是平行四边形呢
大家都困惑了……
复习引入
问题1 平行四边形的定义是什么?有什么作用?
两组对边分别平行的四边形叫平行四边形.
问题2 除了两组对边分别平行,平行四边形还有哪些性质?
边:平行四边形的对边相等.
角:平行四边形的对角相等.
对角线:平行四边形的对角线互相平分.
问题3 平行四边形上面的三条性质的逆命题各是什么?
两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
思考 我们得到的这些逆命题是否都成立?这节课我们一起探讨一下吧.
互助探究
探究点一:平行四边形的判定定理1
已知: 四边形ABCD中,AB=DC,AD=BC.
求证: 四边形ABCD是平行四边形.
归纳总结
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
探究点二:平行四边形的判定定理2
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
归纳总结
平行四边形的判定定理:
两组对角分别相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
探究点三:平行四边形的判定定理3
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边 形ABCD是平行四边形.
归纳总结
平行四边形的判定定理:
对角线互相平分的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
例题精讲
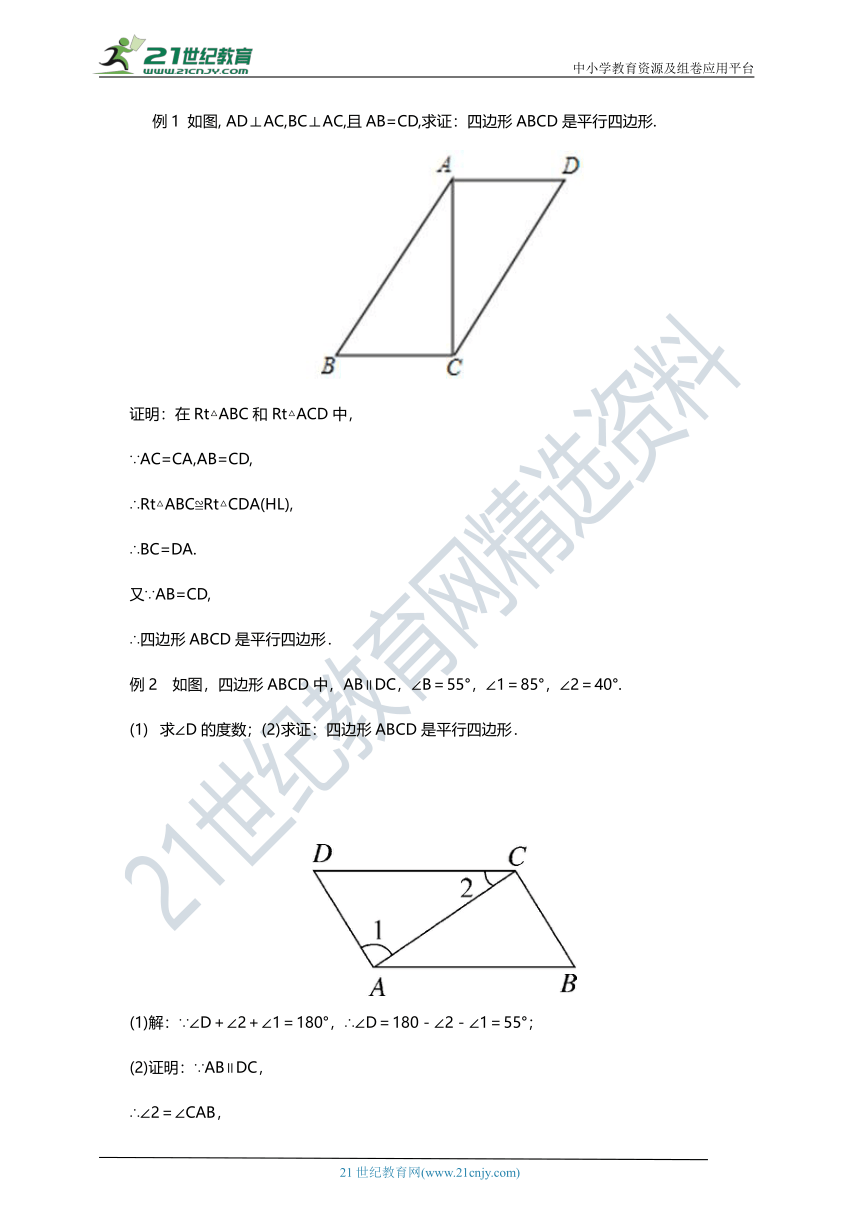
例1 如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△ACD中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
例2 如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
求∠D的度数;(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,∴∠D=180-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
例三 见教材46页例3
跟踪练习
教材47页练习1、2题
课堂小结
平行四边形判定1:
定义法:两组对边分别平行的四边形叫平行四边形.
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
课堂检测
1. 根据下列条件,不能判定一个四边形为平行四边形的是( )
A. 两组对边分别相等
B . 两条对角线互相平分
C . 两条对角线相等
D . 两组对边分别平行
2.能判定四边形ABCD是平行四边形的条件:∠A:∠B:∠C:∠D的值为( )
3. 如图所示,△ABC是等边三角形,P是其内任意一点,PD//AB,PE//BC,PF//AC,若△ABC的周长为24,则PD+PE+PF= .
课后作业
必做题:教材第50页第5、6题;
选做题:教材第51页第13题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
18.1.2平行四边形的判定
第1课时 平行四边形的判定1
核心素养目标:
1.在探索平行四边形的判别条件中,理解并掌握用边、对角线来判定平行四边形的方法.
2.会综合运用平行四边形的判定方法和性质来解决问题.
3.培养用类比、逆向联想及运动的思维方法来研究问题.
教学重难点:
重点:平行四边形的判定方法及应用.
难点:平行四边形的判定定理与性质定理的灵活应用.
教学过程:
问题导入
学行四边形之后,小明回家用细木棒钉制了一个平行四边形.第二天,小明拿着自己动手做的平行四边形向同学们展示.
小辉却问:你凭什么确定这四边形就是平行四边形呢
大家都困惑了……
复习引入
问题1 平行四边形的定义是什么?有什么作用?
两组对边分别平行的四边形叫平行四边形.
问题2 除了两组对边分别平行,平行四边形还有哪些性质?
边:平行四边形的对边相等.
角:平行四边形的对角相等.
对角线:平行四边形的对角线互相平分.
问题3 平行四边形上面的三条性质的逆命题各是什么?
两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
思考 我们得到的这些逆命题是否都成立?这节课我们一起探讨一下吧.
互助探究
探究点一:平行四边形的判定定理1
已知: 四边形ABCD中,AB=DC,AD=BC.
求证: 四边形ABCD是平行四边形.
归纳总结
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
探究点二:平行四边形的判定定理2
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
归纳总结
平行四边形的判定定理:
两组对角分别相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
探究点三:平行四边形的判定定理3
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边 形ABCD是平行四边形.
归纳总结
平行四边形的判定定理:
对角线互相平分的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
例题精讲
例1 如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△ACD中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
例2 如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
求∠D的度数;(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,∴∠D=180-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
例三 见教材46页例3
跟踪练习
教材47页练习1、2题
课堂小结
平行四边形判定1:
定义法:两组对边分别平行的四边形叫平行四边形.
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
课堂检测
1. 根据下列条件,不能判定一个四边形为平行四边形的是( )
A. 两组对边分别相等
B . 两条对角线互相平分
C . 两条对角线相等
D . 两组对边分别平行
2.能判定四边形ABCD是平行四边形的条件:∠A:∠B:∠C:∠D的值为( )
3. 如图所示,△ABC是等边三角形,P是其内任意一点,PD//AB,PE//BC,PF//AC,若△ABC的周长为24,则PD+PE+PF= .
课后作业
必做题:教材第50页第5、6题;
选做题:教材第51页第13题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
