18.1.1 第1课时 平行四边形的边、角的特征 课件(共28张PPT)
文档属性
| 名称 | 18.1.1 第1课时 平行四边形的边、角的特征 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 14:41:50 | ||
图片预览






文档简介
(共28张PPT)
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
18.1平行四边形
第1课时 平行四边形的边、角的特征
18.1.1平行四边形的性质
理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质;
核心素养目标:
会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证;
培养学生发现问题、解决问题的能力及逻辑推理能力.
图片引入:
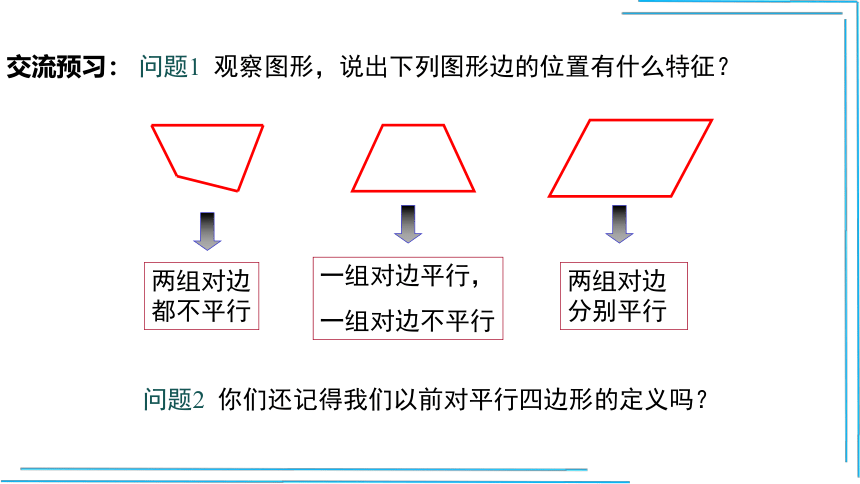
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
问题1 观察图形,说出下列图形边的位置有什么特征?
问题2 你们还记得我们以前对平行四边形的定义吗?
交流预习:
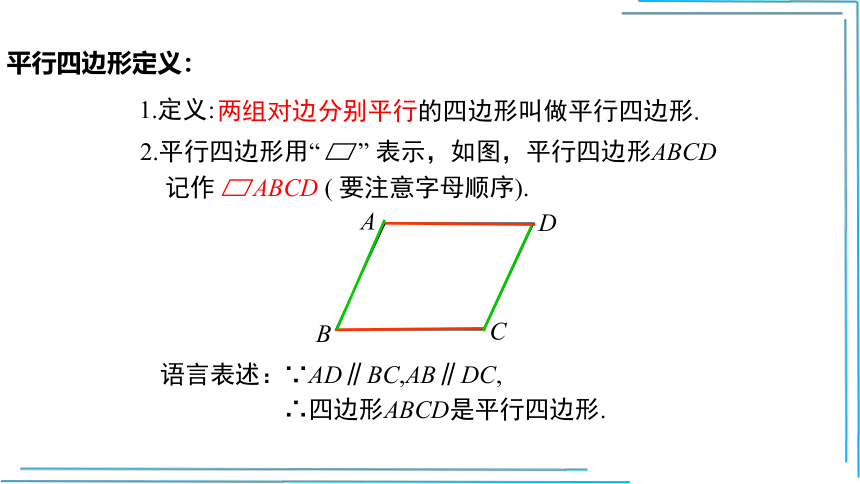
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形用“ ” 表示,如图,平行四边形ABCD
记作 ABCD ( 要注意字母顺序).
1.定义:
A
B
D
C
语言表述:
∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
平行四边形定义:
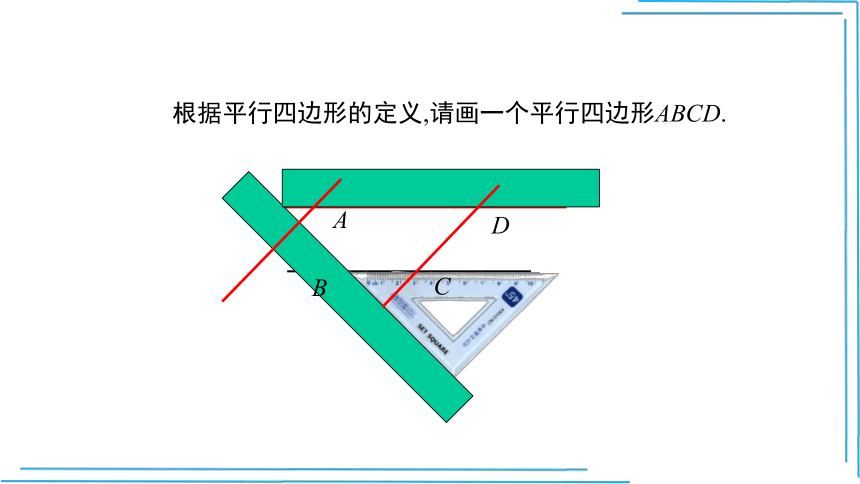
根据平行四边形的定义,请画一个平行四边形ABCD.
D
A
B
C
问题2:对于平行四边形,从定义出发,我们知道平形四边形 的两组对边分别平行,除此之外,它的边之间还有什么关系?它的角之间有什么关系?
度量一下,和你的猜想一致吗?
给出图形定义→研究图形性质→探索图形判定条件
问题1:回忆我们的学习经历,研究几何图形的一般思路是什么?
猜想:平行四边形对角相等,对边相等.
互助探究:
A
B
C
D
活动 1 请用尺子等工具度量你手中平行四边形的四条边,并记录下数据,你能发现AB与DC,AD与BC之间的数量关系吗
测得AB=DC,AD=BC.
探究活动:
A
B
C
D
测得∠A =∠C,∠B =∠D.
活动2 请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A与∠C,∠B与 ∠D之间的数量关系吗
猜想 平行四边形的两组对边,两组对角有什么数量关系?
两组对边及两组对角分别相等.
怎样证明这个猜想呢?
探究活动:
证明:如图,连接AC
∵AD∥BC,AB ∥ CD
∴∠1=∠2,∠3=∠4
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA
∴AD=CD,AB=CD,
∠B=∠D
请同学们自己证明∠BAD=∠DCB.
上述猜想涉及线段相等、角相等、我们知道,利用三角形全等得出全等三角形的对应边、对应角都相等,是证明线段相等、角相等的一种重要的方法,为此,我们通过添加辅助线,构造两个三角形,通过三角形全等进行证明.
说理证明:
A
B
C
D
1
4
3
2
由上面知,△ABC≌△CDA ∴ ∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB.
说理证明:
求证:∠BAD=∠DCB
思考 不添加辅助线,你能否直接运用平行四边形的定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
说理证明:
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
A
B
C
D
平行四边形的性质:
例1 如图,在□ABCD中
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______。
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
(1)平行四边形的对角相等;(2)平行四边形的邻角互补;
(3)平行四边形的一组邻边之和等于周长的一半,反之,周长=2倍邻边之和.
归纳
例题精讲:
D
A
B
C
F
E
证明:
平行四边形为证明线段及角相等提供了一种新的思路.
归纳:
例题精讲:
C
B
F
E
A
D
若m // n,作 AB // CD // EF,分别交 m于A,C,E,交 n于B,D,F.
由平行四边形的性质得AB=CD=EF.
两条平行线之间的平行线段相等.
m
n
由平行四边形的定义易知四边形ABDC,CDFE均为平行四边形.
距离是几何中的重要度量之一,前面我们已经学习了点与点之间的距离、点到直线的距离,在此基础上,我们结合平行四边形的概念和性质,介绍两条平行线之间的距离.
两条平行线间的距离相等.
若m // n,AB , CD , EF垂直于 n,交n于B , D , F , 交 m于A , C , E.
B
F
E
A
n
m
C
D
同前面易得AB=CD=EF.
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离
点到直线的距离
教材43页练习
1.在□ABCD中.
(1)已知AB=5,BC=3,则它的周长= ______.
(2)已知∠A=38°,则∠B=______ ,∠C=______ ,∠D=______.
2如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
16
跟踪练习:
38°
142°
142°
AD=BC
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的距离相等,
两条平行线间的平行线段也相等
两组对角分别相等,邻角互补
课堂小结:
1.在□ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A .45° B. 55° C. 65° D. 75°
A
A
B
C
M
D
课堂检测:
2.判断题(对的在括号内填“√”,错的填“×”):
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°. ( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠C=145°. ( )
√
√
√
×
×
×
课堂检测:
3.在□ABCD中, ∠A: ∠B: ∠C=1:2:1,则∠D等于 .
120°
4.如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
10
课堂检测:
5.有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=60cm.
∴ED=AD-AE=80-60=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
课堂检测:
课后作业:
必做题:习题18.1第1,2,7题.
选做题:习题18.1第8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十八章 平行四边形
18.1平行四边形
第1课时 平行四边形的边、角的特征
18.1.1平行四边形的性质
理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质;
核心素养目标:
会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证;
培养学生发现问题、解决问题的能力及逻辑推理能力.
图片引入:
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
问题1 观察图形,说出下列图形边的位置有什么特征?
问题2 你们还记得我们以前对平行四边形的定义吗?
交流预习:
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形用“ ” 表示,如图,平行四边形ABCD
记作 ABCD ( 要注意字母顺序).
1.定义:
A
B
D
C
语言表述:
∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
平行四边形定义:
根据平行四边形的定义,请画一个平行四边形ABCD.
D
A
B
C
问题2:对于平行四边形,从定义出发,我们知道平形四边形 的两组对边分别平行,除此之外,它的边之间还有什么关系?它的角之间有什么关系?
度量一下,和你的猜想一致吗?
给出图形定义→研究图形性质→探索图形判定条件
问题1:回忆我们的学习经历,研究几何图形的一般思路是什么?
猜想:平行四边形对角相等,对边相等.
互助探究:
A
B
C
D
活动 1 请用尺子等工具度量你手中平行四边形的四条边,并记录下数据,你能发现AB与DC,AD与BC之间的数量关系吗
测得AB=DC,AD=BC.
探究活动:
A
B
C
D
测得∠A =∠C,∠B =∠D.
活动2 请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A与∠C,∠B与 ∠D之间的数量关系吗
猜想 平行四边形的两组对边,两组对角有什么数量关系?
两组对边及两组对角分别相等.
怎样证明这个猜想呢?
探究活动:
证明:如图,连接AC
∵AD∥BC,AB ∥ CD
∴∠1=∠2,∠3=∠4
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA
∴AD=CD,AB=CD,
∠B=∠D
请同学们自己证明∠BAD=∠DCB.
上述猜想涉及线段相等、角相等、我们知道,利用三角形全等得出全等三角形的对应边、对应角都相等,是证明线段相等、角相等的一种重要的方法,为此,我们通过添加辅助线,构造两个三角形,通过三角形全等进行证明.
说理证明:
A
B
C
D
1
4
3
2
由上面知,△ABC≌△CDA ∴ ∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB.
说理证明:
求证:∠BAD=∠DCB
思考 不添加辅助线,你能否直接运用平行四边形的定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
说理证明:
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
A
B
C
D
平行四边形的性质:
例1 如图,在□ABCD中
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______。
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
(1)平行四边形的对角相等;(2)平行四边形的邻角互补;
(3)平行四边形的一组邻边之和等于周长的一半,反之,周长=2倍邻边之和.
归纳
例题精讲:
D
A
B
C
F
E
证明:
平行四边形为证明线段及角相等提供了一种新的思路.
归纳:
例题精讲:
C
B
F
E
A
D
若m // n,作 AB // CD // EF,分别交 m于A,C,E,交 n于B,D,F.
由平行四边形的性质得AB=CD=EF.
两条平行线之间的平行线段相等.
m
n
由平行四边形的定义易知四边形ABDC,CDFE均为平行四边形.
距离是几何中的重要度量之一,前面我们已经学习了点与点之间的距离、点到直线的距离,在此基础上,我们结合平行四边形的概念和性质,介绍两条平行线之间的距离.
两条平行线间的距离相等.
若m // n,AB , CD , EF垂直于 n,交n于B , D , F , 交 m于A , C , E.
B
F
E
A
n
m
C
D
同前面易得AB=CD=EF.
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离
点到直线的距离
教材43页练习
1.在□ABCD中.
(1)已知AB=5,BC=3,则它的周长= ______.
(2)已知∠A=38°,则∠B=______ ,∠C=______ ,∠D=______.
2如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
16
跟踪练习:
38°
142°
142°
AD=BC
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的距离相等,
两条平行线间的平行线段也相等
两组对角分别相等,邻角互补
课堂小结:
1.在□ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A .45° B. 55° C. 65° D. 75°
A
A
B
C
M
D
课堂检测:
2.判断题(对的在括号内填“√”,错的填“×”):
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°. ( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠C=145°. ( )
√
√
√
×
×
×
课堂检测:
3.在□ABCD中, ∠A: ∠B: ∠C=1:2:1,则∠D等于 .
120°
4.如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
10
课堂检测:
5.有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=60cm.
∴ED=AD-AE=80-60=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
课堂检测:
课后作业:
必做题:习题18.1第1,2,7题.
选做题:习题18.1第8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
