2022-2023学年人教版七年级数学下册 5.4平移 同步教学课件(共23张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册 5.4平移 同步教学课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第五章 相交线与平行线
5.4 平移
1.理解平移的概念及决定因素.(难点)
2. 掌握平移的性质及其运用.(重点)
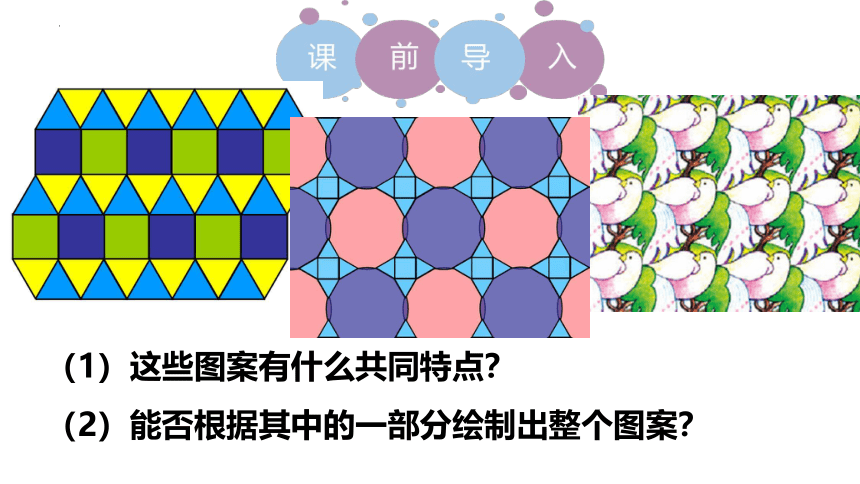
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分绘制出整个图案?
知识点1 平移
探究 如何在一张半透明的纸上,画出一排形状和大小如图的雪人呢?
知识点1 平移
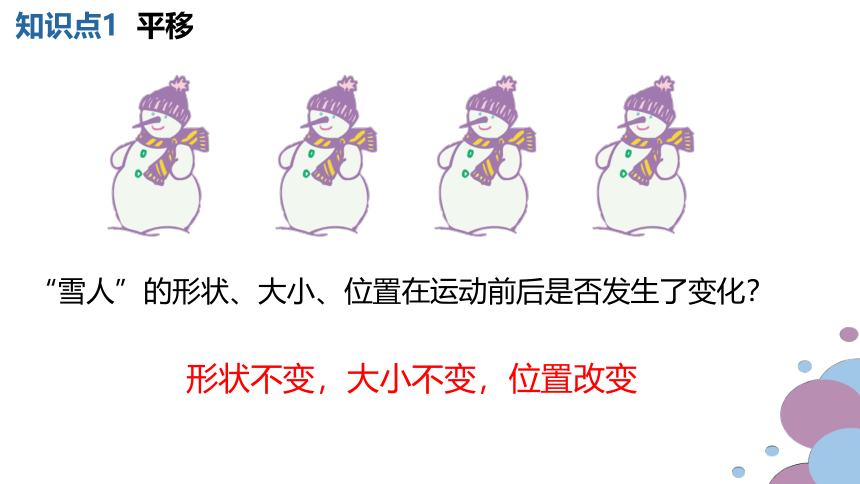
“雪人”的形状、大小、位置在运动前后是否发生了变化?
形状不变,大小不变,位置改变
知识点1 平移
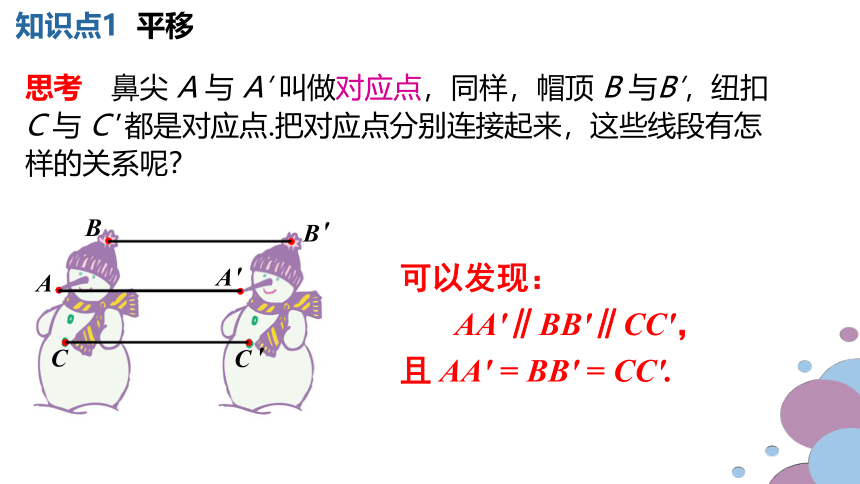
思考 鼻尖 A 与 A′ 叫做对应点,同样,帽顶 B 与B′,纽扣 C 与 C' 都是对应点.把对应点分别连接起来,这些线段有怎样的关系呢?
A
A
'
B
C
B
'
C
'
可以发现:
AA′∥BB′∥CC′,
且 AA′ = BB′ = CC′.
知识点1 平移
把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
2. 连接各组对应点的线段平行(或在同一条直线上)且
相等.
归纳:
图形的这种移动,叫做平移.
知识点1 平移
思考 我们先观看以下几种生活现象,再想一想平移是由什么决定的?
知识点1 平移
1.图形的平移不一定是水平的,也不一定是竖直的.
2.图形的平移由移动的方向和距离决定.
归纳:
知识点2 平移的性质
例1 如图,平移△ABC,使点 A 移动到点 A',画出平移后的△A'B'C'.
解:如图,连接 AA′ ,过点 B 作 AA′ 的平行线 l,在 l 上截取 BB′ = AA′,则点 B′ 就是点 B 的对应点.类似地,作出点 C 的对应点 C' ,得到平移后的△A'B'C'.
B'
l
C'
知识点2 平移的性质
平移的性质:
①平移前后图形的形状和大小完全相同;
②对应线段平行(或在同一直线上)且相等;
③各对应点所连线段平行(或在同一直线上)且相等;
归纳:
1.平移改变的是图形的 ( )
A. 位置 B. 大小
C. 形状 D. 位置、大小和形状
A
1. 下列各组图形,可经平移变换由一个图形得到另一个图形的是( )
A
A B C D
3.下列图案可以由什么图形平移形成?
4. 如图,在方格纸中平移三角形 ABC,使点 A 移到点 M,点 B 和点 C 应移到什么位置?再将点 A 由点 M 移到点 N,分别画出两次平移后的三角形.如果直接平移三角形 ABC,使点 A 移到点 N,它和我们前面得到的三角形位置相同吗?
解:如图:将点 A 移到点 M,则点 B 和点 C 分别移到点B′、点 C′ 处;将点 A 再继续移到点 N 处,则点 B 和点 C 继续移到点 B″、点 C″处.若直接平移三角形 ABC,使点 A 移到点 N,则和前面得到的三角形位置相同.
B'
C'
B''
C''
一、平移
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
二、平移的性质
①平移前后图形的形状和大小完全相同;
②对应线段平行(或在同一直线上)且相等;
③各对应点所连线段平行(或在同一直线上)且相等;
第五章 相交线与平行线
5.4 平移
1.理解平移的概念及决定因素.(难点)
2. 掌握平移的性质及其运用.(重点)
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分绘制出整个图案?
知识点1 平移
探究 如何在一张半透明的纸上,画出一排形状和大小如图的雪人呢?
知识点1 平移
“雪人”的形状、大小、位置在运动前后是否发生了变化?
形状不变,大小不变,位置改变
知识点1 平移
思考 鼻尖 A 与 A′ 叫做对应点,同样,帽顶 B 与B′,纽扣 C 与 C' 都是对应点.把对应点分别连接起来,这些线段有怎样的关系呢?
A
A
'
B
C
B
'
C
'
可以发现:
AA′∥BB′∥CC′,
且 AA′ = BB′ = CC′.
知识点1 平移
把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
2. 连接各组对应点的线段平行(或在同一条直线上)且
相等.
归纳:
图形的这种移动,叫做平移.
知识点1 平移
思考 我们先观看以下几种生活现象,再想一想平移是由什么决定的?
知识点1 平移
1.图形的平移不一定是水平的,也不一定是竖直的.
2.图形的平移由移动的方向和距离决定.
归纳:
知识点2 平移的性质
例1 如图,平移△ABC,使点 A 移动到点 A',画出平移后的△A'B'C'.
解:如图,连接 AA′ ,过点 B 作 AA′ 的平行线 l,在 l 上截取 BB′ = AA′,则点 B′ 就是点 B 的对应点.类似地,作出点 C 的对应点 C' ,得到平移后的△A'B'C'.
B'
l
C'
知识点2 平移的性质
平移的性质:
①平移前后图形的形状和大小完全相同;
②对应线段平行(或在同一直线上)且相等;
③各对应点所连线段平行(或在同一直线上)且相等;
归纳:
1.平移改变的是图形的 ( )
A. 位置 B. 大小
C. 形状 D. 位置、大小和形状
A
1. 下列各组图形,可经平移变换由一个图形得到另一个图形的是( )
A
A B C D
3.下列图案可以由什么图形平移形成?
4. 如图,在方格纸中平移三角形 ABC,使点 A 移到点 M,点 B 和点 C 应移到什么位置?再将点 A 由点 M 移到点 N,分别画出两次平移后的三角形.如果直接平移三角形 ABC,使点 A 移到点 N,它和我们前面得到的三角形位置相同吗?
解:如图:将点 A 移到点 M,则点 B 和点 C 分别移到点B′、点 C′ 处;将点 A 再继续移到点 N 处,则点 B 和点 C 继续移到点 B″、点 C″处.若直接平移三角形 ABC,使点 A 移到点 N,则和前面得到的三角形位置相同.
B'
C'
B''
C''
一、平移
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
二、平移的性质
①平移前后图形的形状和大小完全相同;
②对应线段平行(或在同一直线上)且相等;
③各对应点所连线段平行(或在同一直线上)且相等;
