2022-2023学年苏科版七年级数学下册7.5多边形的内角和与外角和(第1课时)同步精品课件 (共24张ppt)
文档属性
| 名称 | 2022-2023学年苏科版七年级数学下册7.5多边形的内角和与外角和(第1课时)同步精品课件 (共24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 00:00:00 | ||
图片预览





文档简介
第七章 · 平面图形的认识(二)
7.5 多边形的内角和与外角和(1)
第1课时 三角形的内角和
通过实践操作感受、理解并掌握“三角形的内角和为180°”,能运用这一性质进行计算和说理.
学习目标
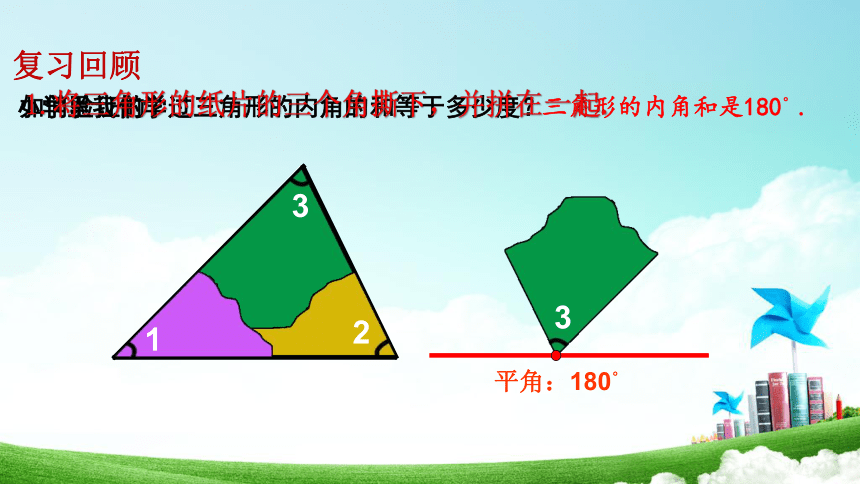
小学里我们学过三角形的内角的和等于多少度?
复习回顾
三角形的内角和是180°.
如何验证的?
1.将三角形的纸片的三个角撕下,并拼在一起.
3
2
3
1
平角:180°
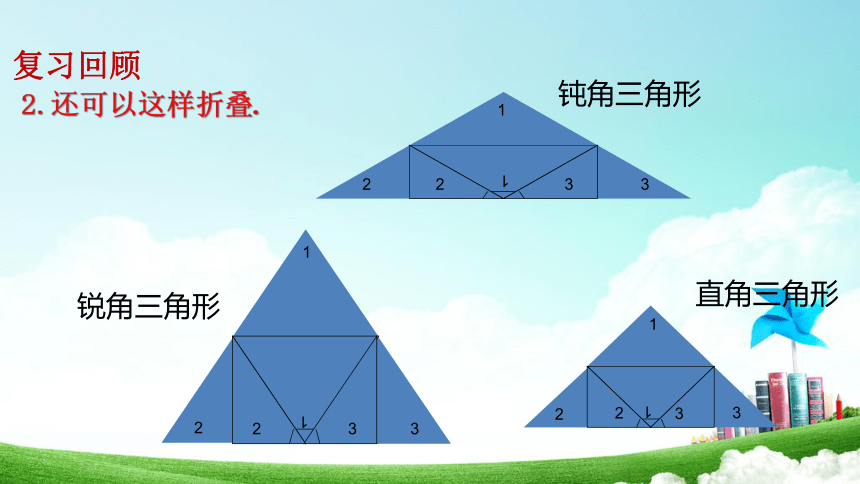
2.还可以这样折叠.
复习回顾
2
1
2
2
3
3
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
复习回顾
3.用量角器度量
请每位同学在课堂笔记本上任意画一个三角形,用量角器量出各内角的度数,并求它们的和.
48°
72°
60°
60 ° +48 ° +72 ° =180 °
知识窗
帕斯卡,法国数学家.早在300多年前这位科学家就已经发现了任何三角形的内角和是180°,而他当时才12岁.
新知探究
A
B
C
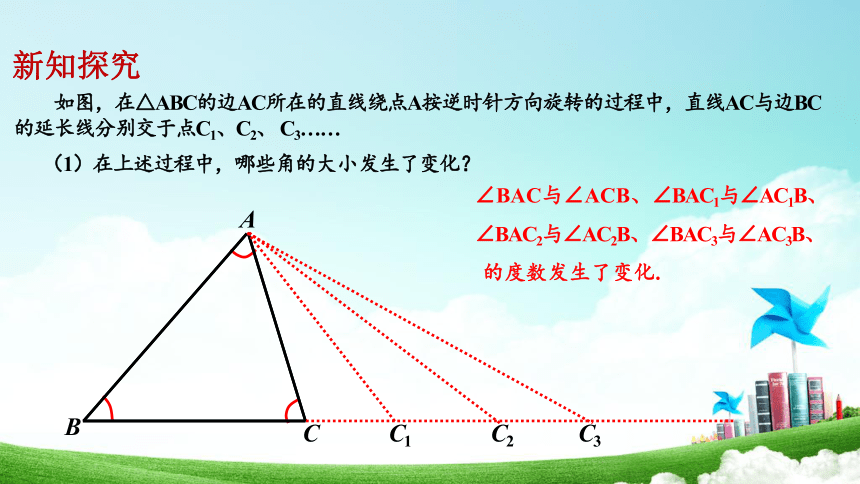
如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点C1、C2、 C3……
C1
C2
C3
(1)在上述过程中,哪些角的大小发生了变化?
∠BAC与∠ACB、∠BAC1与∠AC1B、∠BAC2与∠AC2B、∠BAC3与∠AC3B、
的度数发生了变化.
新知探究
A
B
C
如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点C1、C2、 C3……
C1
C2
C3
(2)度量∠BAC与∠ACB,并求它们的和;度量∠BAC1与∠AC1B、∠BAC2与∠AC2B、∠BAC3与∠AC3B、……并分别求它们的和,你发现了什么?
∠BACn与∠ACnB的度数之和始终不变.
∠BACn的度数逐渐变大.
∠ ACnB的度数逐渐变小.
60 ° +72 ° =132 °
C ’
新知探究
A
B
C
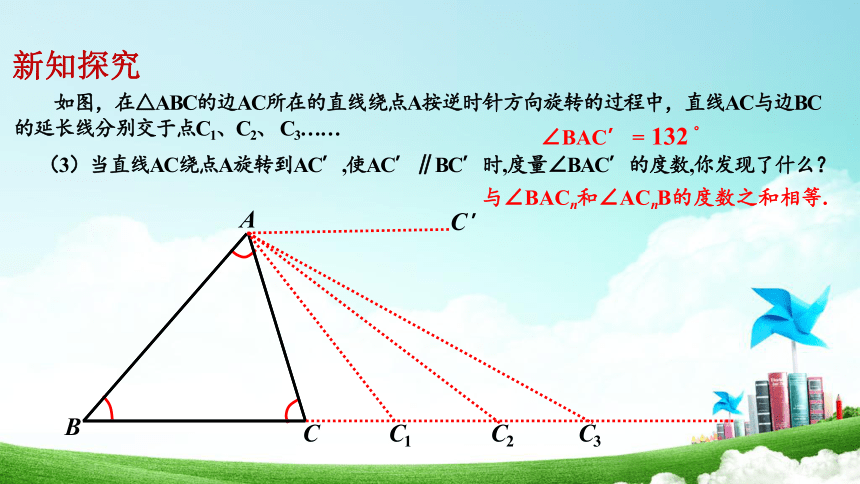
如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点C1、C2、 C3……
C1
C2
C3
(3)当直线AC绕点A旋转到AC’,使AC’∥BC’时,度量∠BAC’的度数,你发现了什么?
∠BAC’ = 132 °
与∠BACn和∠ACnB的度数之和相等.
新知探究
A
B
C
观察下图,请你思考,能通过平行线的性质说明三角形的三个内角和等于180°吗?
C1
C2
C3
C ’
理由如下:
∵AC ’∥BC
∴∠C AC ’=∠ C ,
∠BAC ’+∠B=180°
又∵∠ BAC ’ +∠B
= ∠BAC+ C AC ’+∠C
∴∠B+∠BAC+∠C=180°
借助平行线可以改变角的位置不改变角的大小.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
你还能想到其他方法吗?试一试.
新知探究
A
B
C
A
B
C
添加辅助线思路:
1.构造平角
2.利用平行线转移角
三角形的内角和是180°.
证明:过点A作AD∥BC
∵AD∥BC
∴∠B=∠1,∠C=∠2
∵∠1+∠BAC+∠2=180°
∴∠B+∠BAC+∠C=180°
D
1
2
F
E
符号语言:
在△ABC中,
∠ABC+∠ACB+∠BAC=180°
新知巩固
在△ABC中,
(1)∠A=52°,∠B=118°,求∠C的度数;
解:(1)在△ABC中
∵∠A+∠B+∠C=180°、 ∠A=52°,∠B=118°
∴∠C=180°-∠A-∠B
=180°- 52° - 118°
=10°.
新知巩固
在△ABC中,
(2) ∠C=90°,∠A-∠B=20°,求∠B的度数;
解:(2)设∠B=x,则∠A=x+20°.
∵∠A+∠B+∠C=180°、 ∠C=90° ,
∴x+20°+x+ 90° =90°,
解得x=35°,即∠B=35°
归纳:依据“三角形的内角和是180°”构造方程,是求三角形
各个内角的度数的常用方法.
新知应用
例1.在△ABC中,∠A=40°,∠B=∠C,求∠C的度数.
A
C
B
解:在△ABC中
∠A+∠B+∠C=180°、 ∠A=40°
∴∠B+∠C=180°-∠A
=180°-40°
=140°
∵∠B=∠C
∴∠B+∠C=2∠C=140°
∴∠C=70°
P
)
(
1
2
变式:在例1条件下,若P为△ABC内一点,∠1=∠2,求∠BPC的度数.
新知探究
1
2
例2.如图,AC、BD相交于点O,∠A与∠B的和等于∠C与∠D的和吗?为什么?
C
B
A
D
O
解:在△ABO中,
∵ ∠ A+∠B+∠1 =180°
∴ ∠A+∠B=180 ° -∠1
在△CDO中,
∵ ∠C+∠D+∠2 = 180 °
∴ ∠C+∠D =180 ° -∠2
又 ∵ ∠1 = ∠2
∴ ∠ A+∠B=∠C+∠D
变式1:如图,若∠A=50°,∠B=32°,∠C=45°,求∠D的度数.
新知探究
变式2:如下图,∠A与∠B的和等于∠OCD与∠ODC的和吗?为什么?
C
B
A
D
O
例3.如图,△ABC的角平分线BD、CE相交于点P,∠A=70°,求∠BPC的度数.
新知应用
C
B
A
D
E
P
解:在△ABC中,
因为∠A+∠ABC+∠ACB=180°、∠A=70°,
所以∠ABC+∠ACB=180°-∠A=180°-70°=110°
因为BD、CE分别平分∠ABC、∠ACB,
所以∠1+∠2=????????∠ABC+ ????????∠ACB= ????????×110°=55°
在△PBC中,
所以∠BPC=180°-(∠1+∠2)=180°-55°=125°
?
1
2
∠BPC= 90°+????????∠????
?
变式:∠A=n°,求∠BPC的度数.
课堂小结
本节课你有什么收获?
课堂检测
(2)在直角△ABC中,∠A=30°,则∠B=_______________
1.根据下图填空:
(1)n=_____; (2)x=_____; (3)y=_____.
81°
72°
n°
(1)
x°
x°
(2)
∟
31°
y°
(3)
122°
27°
29°
59°
A
B
C
A
A
B
B
C
C
2.(1)在直角△ABC中,∠C=90°,∠A+∠B=____.
90°
在直角△ABC中
∵∠A+∠B+∠C=180°∠C=90°
∴∠A+∠B=90°
解:
A
C
B
60°或90°
课堂检测
3.如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )
A.30° B.40° C.50° D.60°
B
C
B
A
D
E
课堂检测
4.将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.70° B.75° C.80° D.85°
B
课堂检测
5.在△ABC中,∠A∶∠B∶∠C=1∶1∶7,求∠A,∠B和∠C的度数.
解:设∠A=x,则∠B=x,∠C=7x,
根据题意,得x+x+7x=180°,解得x=20°,
∴∠A=20°,∠B=20°,∠C=140°.
课堂检测
6.如图(1)是一个五角星,你会求∠A+∠B+∠C+∠D+∠E的值吗?
A
C
D
E
B
2
1
╮
╰
解:由例2可知:
∠1+∠2=∠B+∠E
∵在△ACD中,
∠ A+∠ACD+∠ADC =180°
∴∠A+∠ACE+∠1+∠2+∠ADB=180°
即:∠A+ ∠B+ ∠C+ ∠D+ ∠E=180°
变式1:上图中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化?
如图(2)说明你的结论的正确性.
A
B
C
E
D
课堂检测
变式2:如图,D、E两点在∠BAC的内部,B、F、E、M四点在同一直线上,
求:∠A+∠ABF+∠ACD+∠D+∠DEF的度数.
C
B
A
D
M
F
E
1
2
解:由例2可知:
∠1+∠2=∠D+∠DEF
∵在△ABC中,
∠A+∠ABC+∠ACB =180°
∴∠A+∠ABF+∠1+∠2+∠ACD=180 °
即∠A+∠ABF+∠ACD+∠D+∠DEF=180 °
7.5 多边形的内角和与外角和(1)
第1课时 三角形的内角和
通过实践操作感受、理解并掌握“三角形的内角和为180°”,能运用这一性质进行计算和说理.
学习目标
小学里我们学过三角形的内角的和等于多少度?
复习回顾
三角形的内角和是180°.
如何验证的?
1.将三角形的纸片的三个角撕下,并拼在一起.
3
2
3
1
平角:180°
2.还可以这样折叠.
复习回顾
2
1
2
2
3
3
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
复习回顾
3.用量角器度量
请每位同学在课堂笔记本上任意画一个三角形,用量角器量出各内角的度数,并求它们的和.
48°
72°
60°
60 ° +48 ° +72 ° =180 °
知识窗
帕斯卡,法国数学家.早在300多年前这位科学家就已经发现了任何三角形的内角和是180°,而他当时才12岁.
新知探究
A
B
C
如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点C1、C2、 C3……
C1
C2
C3
(1)在上述过程中,哪些角的大小发生了变化?
∠BAC与∠ACB、∠BAC1与∠AC1B、∠BAC2与∠AC2B、∠BAC3与∠AC3B、
的度数发生了变化.
新知探究
A
B
C
如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点C1、C2、 C3……
C1
C2
C3
(2)度量∠BAC与∠ACB,并求它们的和;度量∠BAC1与∠AC1B、∠BAC2与∠AC2B、∠BAC3与∠AC3B、……并分别求它们的和,你发现了什么?
∠BACn与∠ACnB的度数之和始终不变.
∠BACn的度数逐渐变大.
∠ ACnB的度数逐渐变小.
60 ° +72 ° =132 °
C ’
新知探究
A
B
C
如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点C1、C2、 C3……
C1
C2
C3
(3)当直线AC绕点A旋转到AC’,使AC’∥BC’时,度量∠BAC’的度数,你发现了什么?
∠BAC’ = 132 °
与∠BACn和∠ACnB的度数之和相等.
新知探究
A
B
C
观察下图,请你思考,能通过平行线的性质说明三角形的三个内角和等于180°吗?
C1
C2
C3
C ’
理由如下:
∵AC ’∥BC
∴∠C AC ’=∠ C ,
∠BAC ’+∠B=180°
又∵∠ BAC ’ +∠B
= ∠BAC+ C AC ’+∠C
∴∠B+∠BAC+∠C=180°
借助平行线可以改变角的位置不改变角的大小.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
你还能想到其他方法吗?试一试.
新知探究
A
B
C
A
B
C
添加辅助线思路:
1.构造平角
2.利用平行线转移角
三角形的内角和是180°.
证明:过点A作AD∥BC
∵AD∥BC
∴∠B=∠1,∠C=∠2
∵∠1+∠BAC+∠2=180°
∴∠B+∠BAC+∠C=180°
D
1
2
F
E
符号语言:
在△ABC中,
∠ABC+∠ACB+∠BAC=180°
新知巩固
在△ABC中,
(1)∠A=52°,∠B=118°,求∠C的度数;
解:(1)在△ABC中
∵∠A+∠B+∠C=180°、 ∠A=52°,∠B=118°
∴∠C=180°-∠A-∠B
=180°- 52° - 118°
=10°.
新知巩固
在△ABC中,
(2) ∠C=90°,∠A-∠B=20°,求∠B的度数;
解:(2)设∠B=x,则∠A=x+20°.
∵∠A+∠B+∠C=180°、 ∠C=90° ,
∴x+20°+x+ 90° =90°,
解得x=35°,即∠B=35°
归纳:依据“三角形的内角和是180°”构造方程,是求三角形
各个内角的度数的常用方法.
新知应用
例1.在△ABC中,∠A=40°,∠B=∠C,求∠C的度数.
A
C
B
解:在△ABC中
∠A+∠B+∠C=180°、 ∠A=40°
∴∠B+∠C=180°-∠A
=180°-40°
=140°
∵∠B=∠C
∴∠B+∠C=2∠C=140°
∴∠C=70°
P
)
(
1
2
变式:在例1条件下,若P为△ABC内一点,∠1=∠2,求∠BPC的度数.
新知探究
1
2
例2.如图,AC、BD相交于点O,∠A与∠B的和等于∠C与∠D的和吗?为什么?
C
B
A
D
O
解:在△ABO中,
∵ ∠ A+∠B+∠1 =180°
∴ ∠A+∠B=180 ° -∠1
在△CDO中,
∵ ∠C+∠D+∠2 = 180 °
∴ ∠C+∠D =180 ° -∠2
又 ∵ ∠1 = ∠2
∴ ∠ A+∠B=∠C+∠D
变式1:如图,若∠A=50°,∠B=32°,∠C=45°,求∠D的度数.
新知探究
变式2:如下图,∠A与∠B的和等于∠OCD与∠ODC的和吗?为什么?
C
B
A
D
O
例3.如图,△ABC的角平分线BD、CE相交于点P,∠A=70°,求∠BPC的度数.
新知应用
C
B
A
D
E
P
解:在△ABC中,
因为∠A+∠ABC+∠ACB=180°、∠A=70°,
所以∠ABC+∠ACB=180°-∠A=180°-70°=110°
因为BD、CE分别平分∠ABC、∠ACB,
所以∠1+∠2=????????∠ABC+ ????????∠ACB= ????????×110°=55°
在△PBC中,
所以∠BPC=180°-(∠1+∠2)=180°-55°=125°
?
1
2
∠BPC= 90°+????????∠????
?
变式:∠A=n°,求∠BPC的度数.
课堂小结
本节课你有什么收获?
课堂检测
(2)在直角△ABC中,∠A=30°,则∠B=_______________
1.根据下图填空:
(1)n=_____; (2)x=_____; (3)y=_____.
81°
72°
n°
(1)
x°
x°
(2)
∟
31°
y°
(3)
122°
27°
29°
59°
A
B
C
A
A
B
B
C
C
2.(1)在直角△ABC中,∠C=90°,∠A+∠B=____.
90°
在直角△ABC中
∵∠A+∠B+∠C=180°∠C=90°
∴∠A+∠B=90°
解:
A
C
B
60°或90°
课堂检测
3.如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )
A.30° B.40° C.50° D.60°
B
C
B
A
D
E
课堂检测
4.将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.70° B.75° C.80° D.85°
B
课堂检测
5.在△ABC中,∠A∶∠B∶∠C=1∶1∶7,求∠A,∠B和∠C的度数.
解:设∠A=x,则∠B=x,∠C=7x,
根据题意,得x+x+7x=180°,解得x=20°,
∴∠A=20°,∠B=20°,∠C=140°.
课堂检测
6.如图(1)是一个五角星,你会求∠A+∠B+∠C+∠D+∠E的值吗?
A
C
D
E
B
2
1
╮
╰
解:由例2可知:
∠1+∠2=∠B+∠E
∵在△ACD中,
∠ A+∠ACD+∠ADC =180°
∴∠A+∠ACE+∠1+∠2+∠ADB=180°
即:∠A+ ∠B+ ∠C+ ∠D+ ∠E=180°
变式1:上图中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化?
如图(2)说明你的结论的正确性.
A
B
C
E
D
课堂检测
变式2:如图,D、E两点在∠BAC的内部,B、F、E、M四点在同一直线上,
求:∠A+∠ABF+∠ACD+∠D+∠DEF的度数.
C
B
A
D
M
F
E
1
2
解:由例2可知:
∠1+∠2=∠D+∠DEF
∵在△ABC中,
∠A+∠ABC+∠ACB =180°
∴∠A+∠ABF+∠1+∠2+∠ACD=180 °
即∠A+∠ABF+∠ACD+∠D+∠DEF=180 °
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
