等腰三角形的轴对称性

课件23张PPT。等腰三角形的轴对称性(3）温故而知新1.等腰三角形具有哪些性质？3.有一个等腰三角形，它的底边恰 好与腰相等，这样的三角形又具有什么性质？2.如何识别一个三角形是否是等腰
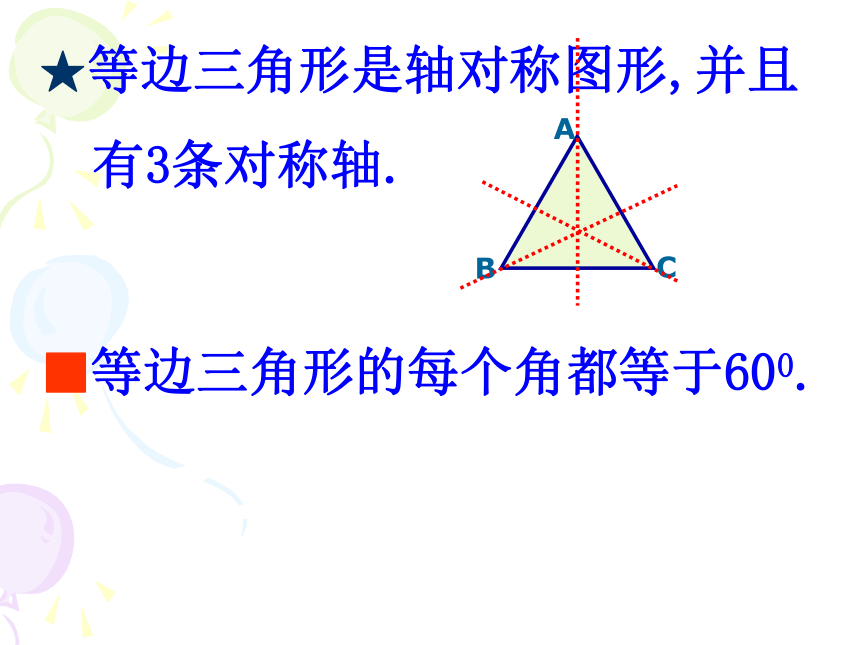
三角形?三边相等的三角形叫做等边三角形或正三角形. 等边三角形是特殊的等腰三角形，它除了具有等腰三角形的一切性质外，还具有哪些特殊的性质呢？ABC★等边三角形是轴对称图形,并且
有3条对称轴.■等边三角形的每个角都等于600.ABC等边三角形性质：
1）等边三角形是轴对称图形,并且有3条
对称轴.
2）等边对等角的性质；
3）“三线合一”的性质；
4）等边三角形的每个内角等于600． 判别一个三角形是等边三角形有哪些方法呢？议一议：
(1)3个角相等的三角形是等边三角形吗?
(2)有两个角是60°的三角形是等边三角
形吗?
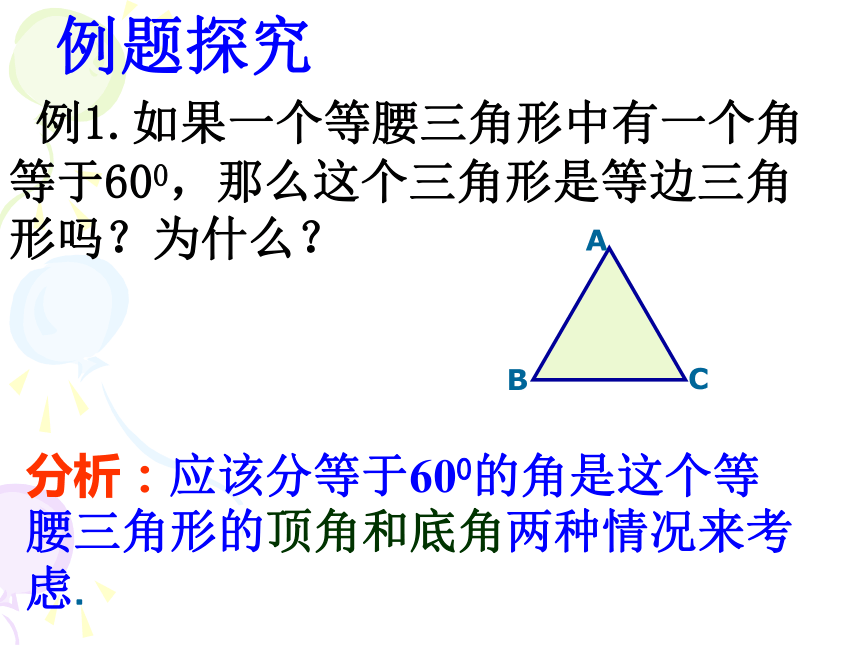
思考1、3个角相等的三角形是等边三角形.2、有两个角等于600的三角形是等边三角形.结论问、有一个角等于600的三角形是等边三角形吗？ 例1.如果一个等腰三角形中有一个角等于600，那么这个三角形是等边三角形吗？为什么？分析：应该分等于600的角是这个等腰三角形的顶角和底角两种情况来考虑.例题探究判定等边三角形的条件1.3个角相等的三角形是等边三角形.2.有两个角等于600的三角形是等边
三角形.3.有一个角等于600的等腰三角形是
等边三角形.观察图中有几条对称轴?
请你画出来.练一练:P28 练习1,2答：有六条对称轴．练一练
如图，P、Q是△ABC的BC边上的
两点,且BP＝PQ＝QC＝AP＝AQ，
求∠BAC的度数.
：如图,在△ABC中,AB=AC,
∠BAC=120°,AD⊥AB,AE⊥AC.
⑴ 图中,等于300的有 ,
等于600的角有 ;P30 11∠B、 ∠C、 ∠BAE、 ∠CAD∠AED、 ∠ADE、 ∠EAD ：如图,在△ABC中,AB=AC,
∠BAC=1200 ,AD⊥AB, AE⊥AC.
⑵ △ADE是等边三角形吗?为什么?
⑶ 在Rt△ABD中,∠B=____,AD=___BD;
在Rt△ACE中 ,有类似结论吗?P30 11△ ADE是等边三角形．300（2）连接MN，试说明△MNC为等边三角形.如图,△ABC和△CDE都是等边三角形, 且点A,C,E在一条直线上.
（1）AD与BE相等吗？为什么？P30 12检测与练习1.等边三角形中，两条中线所夹的钝角的度数为( 　)
　A．120° B．130° C．150°　D．160° A2.如图，在△ABC中,∠C=900,DE是AB的垂直平分线,且∠BAD:∠CAB=1:3，则∠B ＝__________.22.50检测与练习3.如图，等边三角形ABC中，BD=CE，AD与BE相交于点F,则∠AFE的度数为（ ）
A．45° B．55° C．60° D．75°12C4.如图，△ABC是等边三角形，D为AC边上的一点，且∠1=∠2，BD=CE．试说明：△ADE是等边三角形．拓展延伸 等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ ,则△APQ是什么形状的三角形? 试说明你的结论.12选做题 1.用一块等边三角形的硬纸片（如图1）做一个底面为等边三角形且高相等的无盖的盒子（边缝忽略不计，如图2），在△ABC的每个顶点处各需剪掉一个四边形，其中四边形AMDN中,∠MDN的度数为（ ）
A. 1000 B. 1100 C. 1200 D. 1300C拓展延伸 2.以△ABC的边AB、AC为边在△ABC的外部分别作△ABE和等边△ACF，CE与BF相交与点O.求∠EOB的度数.G课堂小结你有什么收获？小测验天高任鸟飞