【核心素养目标】3.2直棱柱、圆锥的侧面展开图 教学设计
文档属性
| 名称 | 【核心素养目标】3.2直棱柱、圆锥的侧面展开图 教学设计 |
|
|
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版版九年级下册数学3.2直棱柱、圆锥的侧面展开图 教学设计
课题 3.2直棱柱、圆锥的侧面展开图 单元 第一单元 学科 数学 年级 九
教材分析 本节课在初中学习平面图形的基础上,继续研究立体图形的知识,本节重点是认识直棱柱、圆锥的侧面展开图,并会计算周长和面积。知道直棱柱的侧面展开图是矩形,圆锥的侧面展开图是扇形。
核心素养分析 本节学习了直棱柱、圆锥的侧面展开图,并会计算侧面展开图的周长和面积。一是认识直棱柱、圆锥的侧面展开图,培养了学生的几何直观的核心素养,二是计算侧面展开图的周长和面积,培养了学生的计算能力。
学习目标 1.理解棱柱的概念,直棱柱各部分的名称及特征;2.理解直棱柱与它的侧面展开图的关系,会求直棱柱的侧面周长和面积 3.掌握圆锥与它的侧面展开图的关系,会求圆锥的侧面周长和面积
重点 理解直棱柱与它的侧面展开图的关系,会求直棱柱的侧面周长和面积
难点 掌握圆锥与它的侧面展开图的关系,会求圆锥的侧面周长和面积
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 当物体的某个面平行于投影面时, 这个面的正投影与该面的形状、大小________________.完全相同 回顾前面学习的知识,温故知新,复习正投影的性质。 温故知新,激发学生兴趣,引入新的内容,让学生开始认识直棱柱、圆锥的侧面展开图。
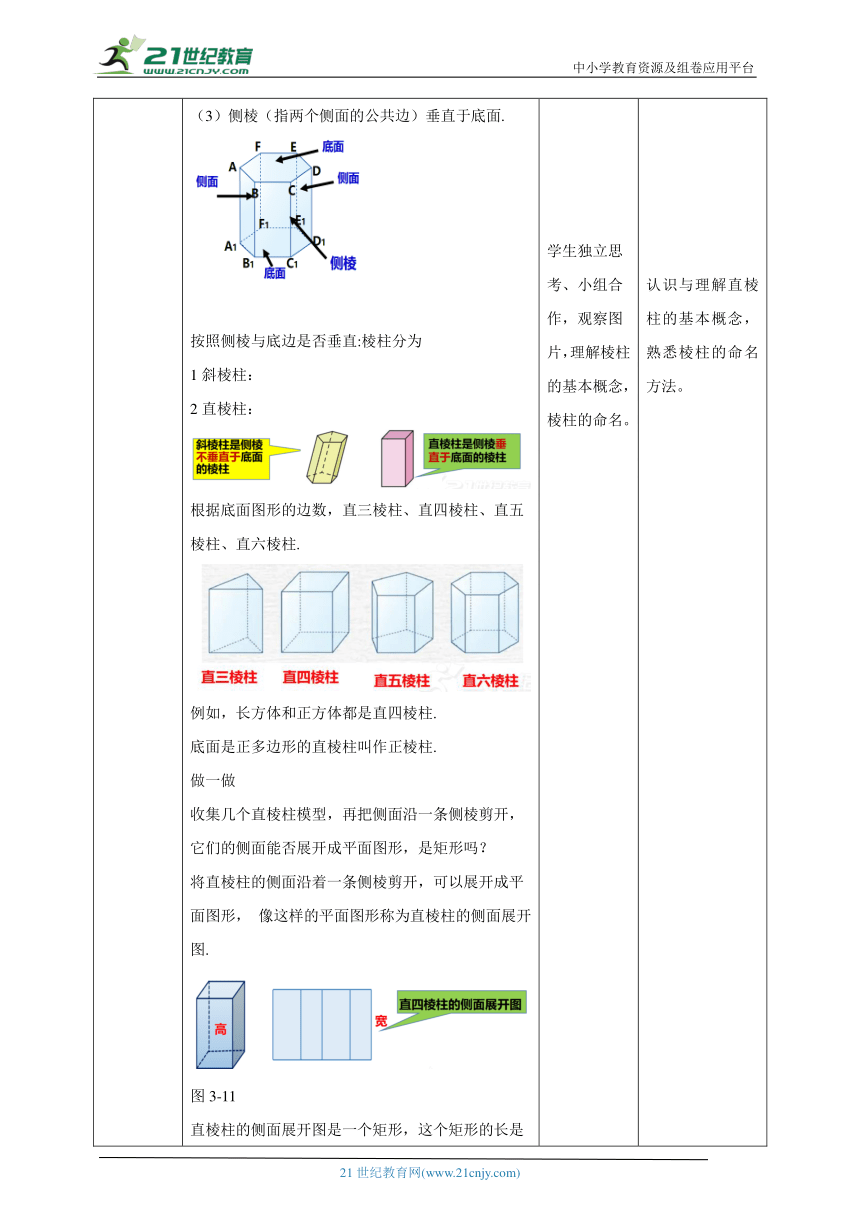
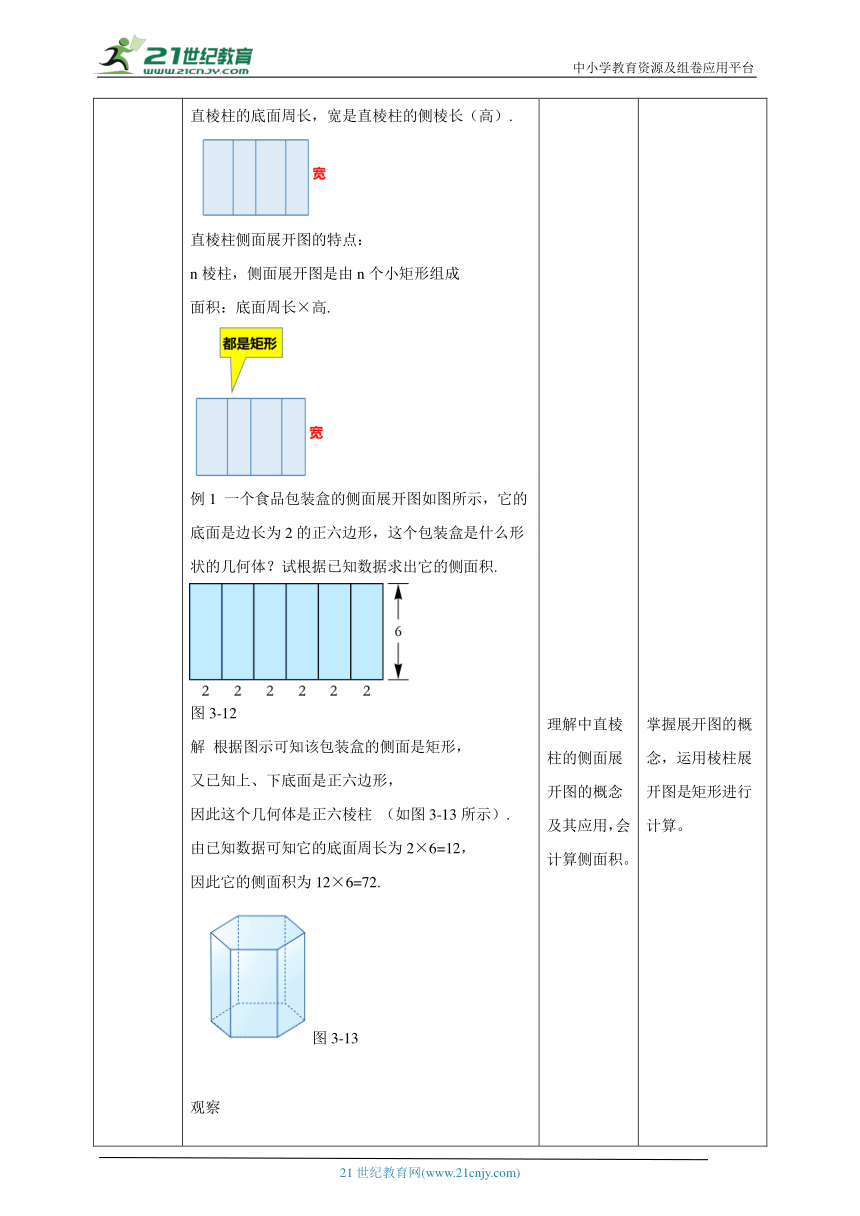
讲授新课 观察下面的立体图形都是棱柱,它们的形状有什么特点? 在几何中,我们把上述这样的立体图形称为直棱柱, 其中“棱” 是指两个面的公共边,它具有以下特征: (1)有两个面互相平行,称它们为底面; (2)其余各个面均为矩形,称它们为侧面; (3)侧棱(指两个侧面的公共边)垂直于底面.按照侧棱与底边是否垂直:棱柱分为1斜棱柱:2直棱柱:根据底面图形的边数,直三棱柱、直四棱柱、直五棱柱、直六棱柱. 例如,长方体和正方体都是直四棱柱. 底面是正多边形的直棱柱叫作正棱柱.做一做收集几个直棱柱模型,再把侧面沿一条侧棱剪开,它们的侧面能否展开成平面图形,是矩形吗?将直棱柱的侧面沿着一条侧棱剪开,可以展开成平面图形, 像这样的平面图形称为直棱柱的侧面展开图. 图3-11直棱柱的侧面展开图是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高).直棱柱侧面展开图的特点:n棱柱,侧面展开图是由n个小矩形组成面积:底面周长×高.例1 一个食品包装盒的侧面展开图如图所示,它的底面是边长为2的正六边形,这个包装盒是什么形状的几何体?试根据已知数据求出它的侧面积.图3-12解 根据图示可知该包装盒的侧面是矩形, 又已知上、下底面是正六边形,因此这个几何体是正六棱柱 (如图3-13所示). 由已知数据可知它的底面周长为2×6=12, 因此它的侧面积为12×6=72.图3-13观察图 3-14 是雕塑与斗笠的形象,它们的形状有什么特点?图 3-14圆锥是由一个底面和一个侧面围成的图形,它的底面是一个圆,连接顶点与底面圆心的线段叫作圆锥的高.圆锥是由一个底面和一个侧面围成的图形,它的底面是一个圆,连接顶点与底面圆心的线段叫作圆锥的高.图3-15圆锥顶点与底面圆上任意一点的连线段都叫作圆锥的母线把圆锥沿它的一条母线剪开,它的侧面可以展开成平面图形,像这样的平面图形称为圆锥的侧面展开图,如图 3-16 所示.圆锥的侧面展开图是一个扇形。这个扇形的半径是圆锥的母线长PA,弧长是底面圆的周长。图 3-16例2 如图3-17,小刚用一张半径为24cm的扇形纸板做一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积S是多少? 图3-17分析 圆锥形帽子的底面周长就是扇形的弧长. 解 扇形的弧长(即底面圆周长)为l=2×π×10=20π(cm). 所以扇形纸板的面积S=12×20π×24=240π(cm2)总结直棱柱的侧面展开图是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高);圆锥的侧面展开图是一个扇形.这个扇形的半径是圆锥的母线长,弧长是圆锥的底面圆的周长. 学生独立思考、小组合作,观察图片,理解棱柱的基本概念,棱柱的命名。 理解中直棱柱的侧面展开图的概念及其应用,会计算侧面积。 学生独立思考,小组合作,理解圆锥的高、母线,侧面展开图是扇形,扇形的半径是圆锥的母线。运用圆锥展开图性质,圆锥形的底面周长就是扇形的弧长,进行计算 认识与理解直棱柱的基本概念,熟悉棱柱的命名方法。 掌握展开图的概念,运用棱柱展开图是矩形进行计算。 理解圆锥展开图与圆锥的关系。熟练运用性质,圆锥形的底面周长就是扇形的弧长。
课堂练习 1.如图是一个粉笔盒的表面展开图,若字母A表示粉笔盒的上盖,B表示侧面,则底面在表面展开图中的位置是( )A. ① B. ② C. ③ D. ④解:根据题意可得,还原为原来的长方体。若字母A表示粉笔盒的上盖,B表示侧面,则底面在表面展开图中的位置是③.故选:C. 2.一种产品的包装盒如图所示,为了生产这种包装盒,需要先画出其表面展开图的纸样(单位cm)(1)如图所示,给出三种纸样甲、乙、丙,在甲、乙、丙中正确的有_乙,丙 ____.(2)利用你所选的一种纸样,求出包装盒的表面积(侧面积和两个底面积的和)和体积.解:(2)表面积=2×(3×13+3×5+13×5)=238(cm2),体积=3×13×5=195(cm3).如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.解:在等腰中,,
,
是的角平分线,
,,
,
,
由弧及线段、、围成图形图中阴影部分的面积;
设圆锥的底面圆的半径为,
根据题意得,解得,
这个圆锥的高. 学生做本节练习,掌握棱柱与圆锥的展开图的性质,教师进行补充,做最后总结。 练习是为了巩固学生对知识的掌握,理解直棱柱、圆锥的侧面展开图。
课堂小结 学生先发言总结,在教师的引导下总结归纳直棱柱、圆锥的侧面展开图性质。 让学生自己对本节知识进行整合归纳,培养学生养成及时总结的习惯,形成自己的知识体系。
板书 课题:3.2 直棱柱、圆锥的侧面展开图1.直棱柱的侧面展开图是矩形2.圆锥的侧面展开图是扇形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
湘教版版九年级下册数学3.2直棱柱、圆锥的侧面展开图 教学设计
课题 3.2直棱柱、圆锥的侧面展开图 单元 第一单元 学科 数学 年级 九
教材分析 本节课在初中学习平面图形的基础上,继续研究立体图形的知识,本节重点是认识直棱柱、圆锥的侧面展开图,并会计算周长和面积。知道直棱柱的侧面展开图是矩形,圆锥的侧面展开图是扇形。
核心素养分析 本节学习了直棱柱、圆锥的侧面展开图,并会计算侧面展开图的周长和面积。一是认识直棱柱、圆锥的侧面展开图,培养了学生的几何直观的核心素养,二是计算侧面展开图的周长和面积,培养了学生的计算能力。
学习目标 1.理解棱柱的概念,直棱柱各部分的名称及特征;2.理解直棱柱与它的侧面展开图的关系,会求直棱柱的侧面周长和面积 3.掌握圆锥与它的侧面展开图的关系,会求圆锥的侧面周长和面积
重点 理解直棱柱与它的侧面展开图的关系,会求直棱柱的侧面周长和面积
难点 掌握圆锥与它的侧面展开图的关系,会求圆锥的侧面周长和面积
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 当物体的某个面平行于投影面时, 这个面的正投影与该面的形状、大小________________.完全相同 回顾前面学习的知识,温故知新,复习正投影的性质。 温故知新,激发学生兴趣,引入新的内容,让学生开始认识直棱柱、圆锥的侧面展开图。
讲授新课 观察下面的立体图形都是棱柱,它们的形状有什么特点? 在几何中,我们把上述这样的立体图形称为直棱柱, 其中“棱” 是指两个面的公共边,它具有以下特征: (1)有两个面互相平行,称它们为底面; (2)其余各个面均为矩形,称它们为侧面; (3)侧棱(指两个侧面的公共边)垂直于底面.按照侧棱与底边是否垂直:棱柱分为1斜棱柱:2直棱柱:根据底面图形的边数,直三棱柱、直四棱柱、直五棱柱、直六棱柱. 例如,长方体和正方体都是直四棱柱. 底面是正多边形的直棱柱叫作正棱柱.做一做收集几个直棱柱模型,再把侧面沿一条侧棱剪开,它们的侧面能否展开成平面图形,是矩形吗?将直棱柱的侧面沿着一条侧棱剪开,可以展开成平面图形, 像这样的平面图形称为直棱柱的侧面展开图. 图3-11直棱柱的侧面展开图是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高).直棱柱侧面展开图的特点:n棱柱,侧面展开图是由n个小矩形组成面积:底面周长×高.例1 一个食品包装盒的侧面展开图如图所示,它的底面是边长为2的正六边形,这个包装盒是什么形状的几何体?试根据已知数据求出它的侧面积.图3-12解 根据图示可知该包装盒的侧面是矩形, 又已知上、下底面是正六边形,因此这个几何体是正六棱柱 (如图3-13所示). 由已知数据可知它的底面周长为2×6=12, 因此它的侧面积为12×6=72.图3-13观察图 3-14 是雕塑与斗笠的形象,它们的形状有什么特点?图 3-14圆锥是由一个底面和一个侧面围成的图形,它的底面是一个圆,连接顶点与底面圆心的线段叫作圆锥的高.圆锥是由一个底面和一个侧面围成的图形,它的底面是一个圆,连接顶点与底面圆心的线段叫作圆锥的高.图3-15圆锥顶点与底面圆上任意一点的连线段都叫作圆锥的母线把圆锥沿它的一条母线剪开,它的侧面可以展开成平面图形,像这样的平面图形称为圆锥的侧面展开图,如图 3-16 所示.圆锥的侧面展开图是一个扇形。这个扇形的半径是圆锥的母线长PA,弧长是底面圆的周长。图 3-16例2 如图3-17,小刚用一张半径为24cm的扇形纸板做一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积S是多少? 图3-17分析 圆锥形帽子的底面周长就是扇形的弧长. 解 扇形的弧长(即底面圆周长)为l=2×π×10=20π(cm). 所以扇形纸板的面积S=12×20π×24=240π(cm2)总结直棱柱的侧面展开图是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高);圆锥的侧面展开图是一个扇形.这个扇形的半径是圆锥的母线长,弧长是圆锥的底面圆的周长. 学生独立思考、小组合作,观察图片,理解棱柱的基本概念,棱柱的命名。 理解中直棱柱的侧面展开图的概念及其应用,会计算侧面积。 学生独立思考,小组合作,理解圆锥的高、母线,侧面展开图是扇形,扇形的半径是圆锥的母线。运用圆锥展开图性质,圆锥形的底面周长就是扇形的弧长,进行计算 认识与理解直棱柱的基本概念,熟悉棱柱的命名方法。 掌握展开图的概念,运用棱柱展开图是矩形进行计算。 理解圆锥展开图与圆锥的关系。熟练运用性质,圆锥形的底面周长就是扇形的弧长。
课堂练习 1.如图是一个粉笔盒的表面展开图,若字母A表示粉笔盒的上盖,B表示侧面,则底面在表面展开图中的位置是( )A. ① B. ② C. ③ D. ④解:根据题意可得,还原为原来的长方体。若字母A表示粉笔盒的上盖,B表示侧面,则底面在表面展开图中的位置是③.故选:C. 2.一种产品的包装盒如图所示,为了生产这种包装盒,需要先画出其表面展开图的纸样(单位cm)(1)如图所示,给出三种纸样甲、乙、丙,在甲、乙、丙中正确的有_乙,丙 ____.(2)利用你所选的一种纸样,求出包装盒的表面积(侧面积和两个底面积的和)和体积.解:(2)表面积=2×(3×13+3×5+13×5)=238(cm2),体积=3×13×5=195(cm3).如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.解:在等腰中,,
,
是的角平分线,
,,
,
,
由弧及线段、、围成图形图中阴影部分的面积;
设圆锥的底面圆的半径为,
根据题意得,解得,
这个圆锥的高. 学生做本节练习,掌握棱柱与圆锥的展开图的性质,教师进行补充,做最后总结。 练习是为了巩固学生对知识的掌握,理解直棱柱、圆锥的侧面展开图。
课堂小结 学生先发言总结,在教师的引导下总结归纳直棱柱、圆锥的侧面展开图性质。 让学生自己对本节知识进行整合归纳,培养学生养成及时总结的习惯,形成自己的知识体系。
板书 课题:3.2 直棱柱、圆锥的侧面展开图1.直棱柱的侧面展开图是矩形2.圆锥的侧面展开图是扇形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
