【新课标】3.2直棱柱、圆锥的侧面展开图 课件(共37张PPT)
文档属性
| 名称 | 【新课标】3.2直棱柱、圆锥的侧面展开图 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 17:37:14 | ||
图片预览








文档简介
(共37张PPT)
3.2直棱柱、圆锥的侧面展开图
湘教版 九年级下
教学内容分析
本节课在初中学习平面图形的基础上,继续研究立体图形的知识,本节重点是认识直棱柱、圆锥的侧面展开图,并会计算周长和面积。知道直棱柱的侧面展开图是矩形,圆锥的侧面展开图是扇形。
教学目标
1.理解棱柱的概念,直棱柱各部分的名称及特征;
2.理解直棱柱与它的侧面展开图的关系,会求直棱柱的侧面周长和面积;(重点)
3.掌握圆锥与它的侧面展开图的关系,会求圆锥的侧面周长和面积.(难点)
核心素养分析
本节学习了直棱柱、圆锥的侧面展开图,并会计算侧面展开图的周长和面积。一是认识直棱柱、圆锥的侧面展开图,培养了学生的几何直观的核心素养,二是计算侧面展开图的周长和面积,培养了学生的计算能力。
新知导入
当物体的某个面平行于投影面时, 这个面的正投影与该面的形状、大小________________.
完全相同
新知讲解
观察
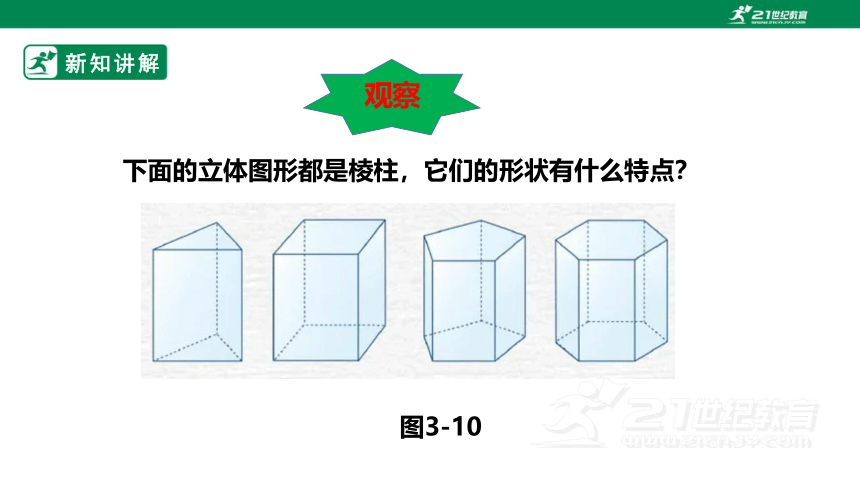
下面的立体图形都是棱柱,它们的形状有什么特点?
图3-10
新知讲解
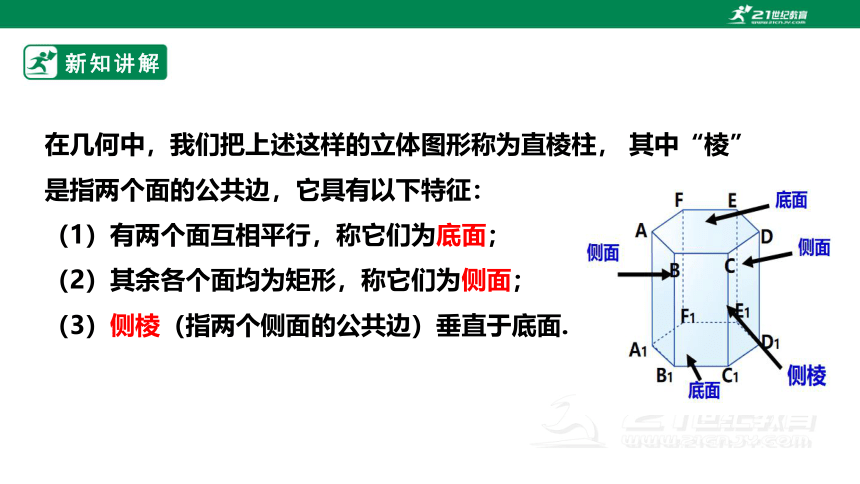
在几何中,我们把上述这样的立体图形称为直棱柱, 其中“棱” 是指两个面的公共边,它具有以下特征:
(1)有两个面互相平行,称它们为底面;
(2)其余各个面均为矩形,称它们为侧面;
(3)侧棱(指两个侧面的公共边)垂直于底面.
新知讲解
按照侧棱与底边是否垂直:棱柱分为
1斜棱柱:
2直棱柱:
斜棱柱是侧棱
不垂直于底面的棱柱
直棱柱是侧棱垂直于底面的棱柱
新知讲解
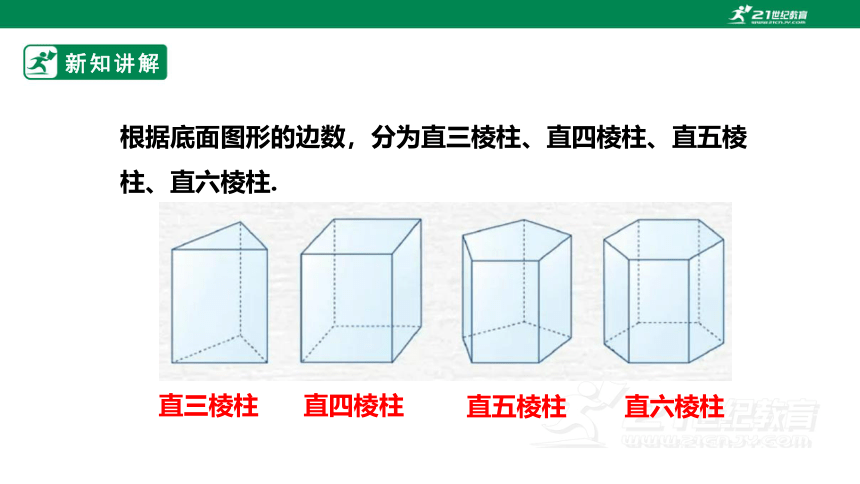
根据底面图形的边数,分为直三棱柱、直四棱柱、直五棱柱、直六棱柱.
直三棱柱
直四棱柱
直五棱柱
直六棱柱
新知讲解
例如,长方体和正方体都是直四棱柱.
底面是正多边形的棱柱叫作正棱柱.
长方体
正方体
收集几个直棱柱模型,再把侧面沿一条侧棱剪开,它们的侧面能否展开成平面图形,是矩形吗?
新知讲解
做一做
新知讲解
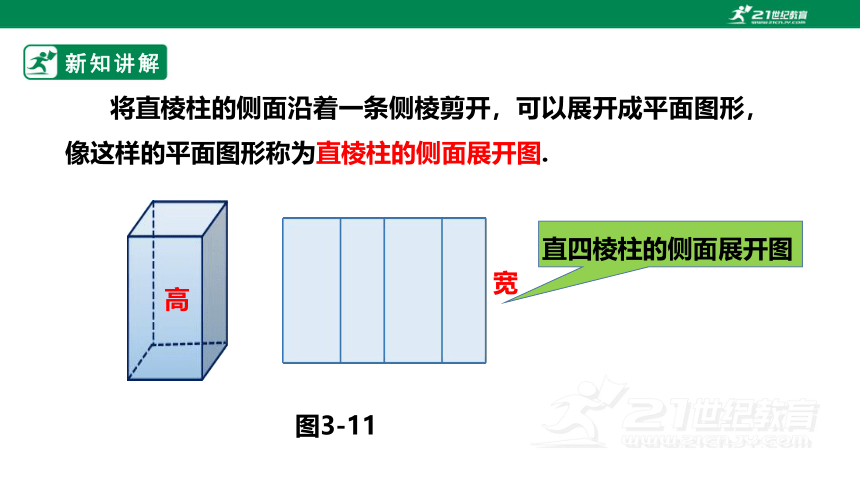
将直棱柱的侧面沿着一条侧棱剪开,可以展开成平面图形, 像这样的平面图形称为直棱柱的侧面展开图.
图3-11
宽
高
直四棱柱的侧面展开图
新知讲解
直棱柱的侧面展开图是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高).
图3-11
宽
直棱柱侧面展开图的特点:
n棱柱,侧面展开图是由n个小矩形组成
面积:底面周长×高.
新知讲解
图3-11
宽
都是矩形
新知讲解
例1 一个食品包装盒的侧面展开图如图所示,它的底面是边长为2的正六边形,这个包装盒是什么形状的几何体?试根据已知数据求出它的侧面积.
图3-12
新知讲解
解 根据图示可知该包装盒的侧面是矩形,
又已知上、下底面是正六边形,
因此这个几何体是正六棱柱 (如图3-13所示).
由已知数据可知它的底面周长为2×6=12,
因此它的侧面积为12×6=72.
图3-13
变式1.如图所示的长方体牛奶包装盒的展开图可能是( )
新知讲解
A. B.
C. D.
B
新知讲解
解:把每一个平面展开图经过折叠后,
A,C,D都不能围成长方体,B可以围成长方体,
故选:B.
新知讲解
图 3-14是雕塑与斗笠的形象,它们的形状有什么特点?
观察
图 3-14
新知讲解
圆锥是由一个底面和一个侧面围成的图形,
它的底面是一个圆,
连接顶点与底面圆心的线段叫作圆锥的高.
图3-15
高
新知讲解
圆锥顶点与底面圆上任意一点的连线段都叫作圆锥的母线
图3-15
高
母线
母线的长度均相等
新知讲解
把圆锥沿它的一条母线剪开,它的侧面可以展开成平面图形,
像这样的平面图形称为圆锥的侧面展开图,如图 3-16 所示.
圆锥的侧面展开图是一个扇形。这个扇形的半径是圆锥的
母线长PA,弧长是底面圆的周长。
高
母线
图 3-16
新知讲解
例2 如图3-17,小刚用一张半径为24cm的扇形纸板做一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积S是多少?
图3-17
新知讲解
分析 圆锥形帽子的底面周长就是扇形的弧长.
解 扇形的弧长(即底面圆周长)为
l=2×π×10=20π(cm).
所以扇形纸板的面积
S=12×20π×24=240π(cm2).
图3-17
直棱柱的侧面展开图是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高);
圆锥的侧面展开图是一个扇形.这个扇形的半径是圆锥的
母线长,弧长是圆锥的底面圆的周长.
新知讲解
总结
1.如图是一个粉笔盒的表面展开图,若字母A表示粉笔盒的上盖,B表示侧面,则底面在表面展开图中的位置是( )
A. ① B. ② C. ③ D. ④
课堂练习
C
解:根据题意可得,还原为原来的长方体。
若字母A表示粉笔盒的上盖,B表示侧面,
则底面在表面展开图中的位置是③.
故选:C.
课堂练习
课堂练习
2.一种产品的包装盒如图所示,为了生产这种包装盒,需要先画出其表面展开图的纸样(单位cm)
(1)如图所示,给出三种纸样甲、乙、丙,在甲、乙、丙中正确的有_____________.
乙,丙
课堂练习
解:
(2)表面积=2×(3×13+3×5+13×5)=238(cm2),
体积=3×13×5=195(cm3).
(2)利用你所选的一种纸样,求出包装盒的表面积(侧面积和两个底面积的和)和体积.
课堂练习
3.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
课堂练习
解:∵在等腰△ABC中,∠BAC=120°,
∴∠B=30°,
∵AD是∠BAC的角平分线,
∴AD⊥BC,BD=CD,
∴BD= AD= ,
∴BC=2BD= ,
∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的
面积=S△ABC-S扇形EAF=
课堂练习
解设圆锥的底面圆的半径为r,
根据题意得
解得r=2,
这个圆锥的高h= .
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
课堂总结
直棱柱、
圆锥的侧面展开图
1直棱柱的侧面展开图是矩形
2圆锥的侧面展开图是扇形
板书设计
3.2 直棱柱、圆锥的侧面展开图
1.直棱柱的侧面展开图是矩形
2.圆锥的侧面展开图是扇形
作业布置
必做题:课本习题 3.2的第1~3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.2直棱柱、圆锥的侧面展开图
湘教版 九年级下
教学内容分析
本节课在初中学习平面图形的基础上,继续研究立体图形的知识,本节重点是认识直棱柱、圆锥的侧面展开图,并会计算周长和面积。知道直棱柱的侧面展开图是矩形,圆锥的侧面展开图是扇形。
教学目标
1.理解棱柱的概念,直棱柱各部分的名称及特征;
2.理解直棱柱与它的侧面展开图的关系,会求直棱柱的侧面周长和面积;(重点)
3.掌握圆锥与它的侧面展开图的关系,会求圆锥的侧面周长和面积.(难点)
核心素养分析
本节学习了直棱柱、圆锥的侧面展开图,并会计算侧面展开图的周长和面积。一是认识直棱柱、圆锥的侧面展开图,培养了学生的几何直观的核心素养,二是计算侧面展开图的周长和面积,培养了学生的计算能力。
新知导入
当物体的某个面平行于投影面时, 这个面的正投影与该面的形状、大小________________.
完全相同
新知讲解
观察
下面的立体图形都是棱柱,它们的形状有什么特点?
图3-10
新知讲解
在几何中,我们把上述这样的立体图形称为直棱柱, 其中“棱” 是指两个面的公共边,它具有以下特征:
(1)有两个面互相平行,称它们为底面;
(2)其余各个面均为矩形,称它们为侧面;
(3)侧棱(指两个侧面的公共边)垂直于底面.
新知讲解
按照侧棱与底边是否垂直:棱柱分为
1斜棱柱:
2直棱柱:
斜棱柱是侧棱
不垂直于底面的棱柱
直棱柱是侧棱垂直于底面的棱柱
新知讲解
根据底面图形的边数,分为直三棱柱、直四棱柱、直五棱柱、直六棱柱.
直三棱柱
直四棱柱
直五棱柱
直六棱柱
新知讲解
例如,长方体和正方体都是直四棱柱.
底面是正多边形的棱柱叫作正棱柱.
长方体
正方体
收集几个直棱柱模型,再把侧面沿一条侧棱剪开,它们的侧面能否展开成平面图形,是矩形吗?
新知讲解
做一做
新知讲解
将直棱柱的侧面沿着一条侧棱剪开,可以展开成平面图形, 像这样的平面图形称为直棱柱的侧面展开图.
图3-11
宽
高
直四棱柱的侧面展开图
新知讲解
直棱柱的侧面展开图是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高).
图3-11
宽
直棱柱侧面展开图的特点:
n棱柱,侧面展开图是由n个小矩形组成
面积:底面周长×高.
新知讲解
图3-11
宽
都是矩形
新知讲解
例1 一个食品包装盒的侧面展开图如图所示,它的底面是边长为2的正六边形,这个包装盒是什么形状的几何体?试根据已知数据求出它的侧面积.
图3-12
新知讲解
解 根据图示可知该包装盒的侧面是矩形,
又已知上、下底面是正六边形,
因此这个几何体是正六棱柱 (如图3-13所示).
由已知数据可知它的底面周长为2×6=12,
因此它的侧面积为12×6=72.
图3-13
变式1.如图所示的长方体牛奶包装盒的展开图可能是( )
新知讲解
A. B.
C. D.
B
新知讲解
解:把每一个平面展开图经过折叠后,
A,C,D都不能围成长方体,B可以围成长方体,
故选:B.
新知讲解
图 3-14是雕塑与斗笠的形象,它们的形状有什么特点?
观察
图 3-14
新知讲解
圆锥是由一个底面和一个侧面围成的图形,
它的底面是一个圆,
连接顶点与底面圆心的线段叫作圆锥的高.
图3-15
高
新知讲解
圆锥顶点与底面圆上任意一点的连线段都叫作圆锥的母线
图3-15
高
母线
母线的长度均相等
新知讲解
把圆锥沿它的一条母线剪开,它的侧面可以展开成平面图形,
像这样的平面图形称为圆锥的侧面展开图,如图 3-16 所示.
圆锥的侧面展开图是一个扇形。这个扇形的半径是圆锥的
母线长PA,弧长是底面圆的周长。
高
母线
图 3-16
新知讲解
例2 如图3-17,小刚用一张半径为24cm的扇形纸板做一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积S是多少?
图3-17
新知讲解
分析 圆锥形帽子的底面周长就是扇形的弧长.
解 扇形的弧长(即底面圆周长)为
l=2×π×10=20π(cm).
所以扇形纸板的面积
S=12×20π×24=240π(cm2).
图3-17
直棱柱的侧面展开图是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高);
圆锥的侧面展开图是一个扇形.这个扇形的半径是圆锥的
母线长,弧长是圆锥的底面圆的周长.
新知讲解
总结
1.如图是一个粉笔盒的表面展开图,若字母A表示粉笔盒的上盖,B表示侧面,则底面在表面展开图中的位置是( )
A. ① B. ② C. ③ D. ④
课堂练习
C
解:根据题意可得,还原为原来的长方体。
若字母A表示粉笔盒的上盖,B表示侧面,
则底面在表面展开图中的位置是③.
故选:C.
课堂练习
课堂练习
2.一种产品的包装盒如图所示,为了生产这种包装盒,需要先画出其表面展开图的纸样(单位cm)
(1)如图所示,给出三种纸样甲、乙、丙,在甲、乙、丙中正确的有_____________.
乙,丙
课堂练习
解:
(2)表面积=2×(3×13+3×5+13×5)=238(cm2),
体积=3×13×5=195(cm3).
(2)利用你所选的一种纸样,求出包装盒的表面积(侧面积和两个底面积的和)和体积.
课堂练习
3.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
课堂练习
解:∵在等腰△ABC中,∠BAC=120°,
∴∠B=30°,
∵AD是∠BAC的角平分线,
∴AD⊥BC,BD=CD,
∴BD= AD= ,
∴BC=2BD= ,
∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的
面积=S△ABC-S扇形EAF=
课堂练习
解设圆锥的底面圆的半径为r,
根据题意得
解得r=2,
这个圆锥的高h= .
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
课堂总结
直棱柱、
圆锥的侧面展开图
1直棱柱的侧面展开图是矩形
2圆锥的侧面展开图是扇形
板书设计
3.2 直棱柱、圆锥的侧面展开图
1.直棱柱的侧面展开图是矩形
2.圆锥的侧面展开图是扇形
作业布置
必做题:课本习题 3.2的第1~3题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
