弧长及扇形的面积(附答案) 中考链接
文档属性
| 名称 | 弧长及扇形的面积(附答案) 中考链接 |  | |
| 格式 | zip | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-20 09:35:41 | ||
图片预览

文档简介
弧长及扇形的面积 中考链接
一.选择题(共8小题)
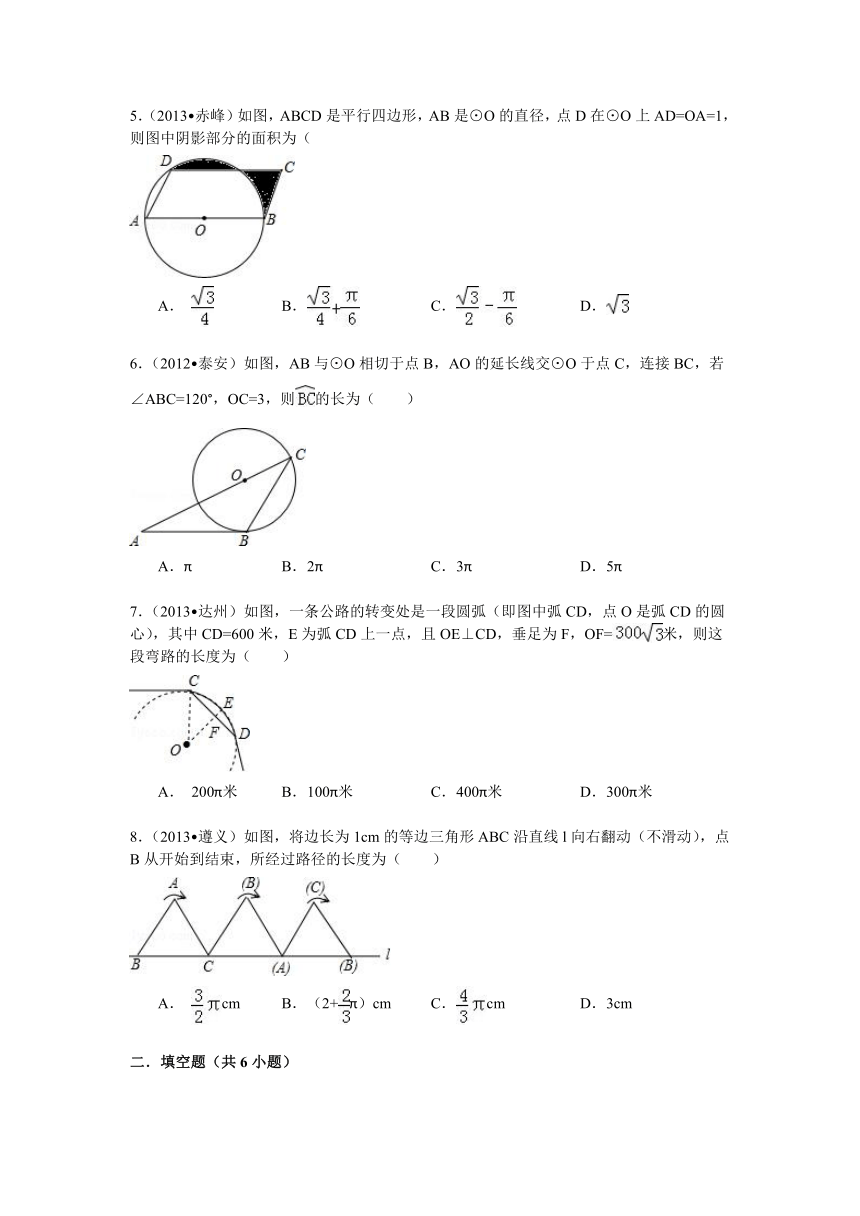
1.(2013 资阳)钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是( )
A. π B. π C. π D. π
2.(2013 葫芦岛)如图,AB是半圆的直径,AB=2,∠B=30°,则的长为( )
A. B. C. π D.
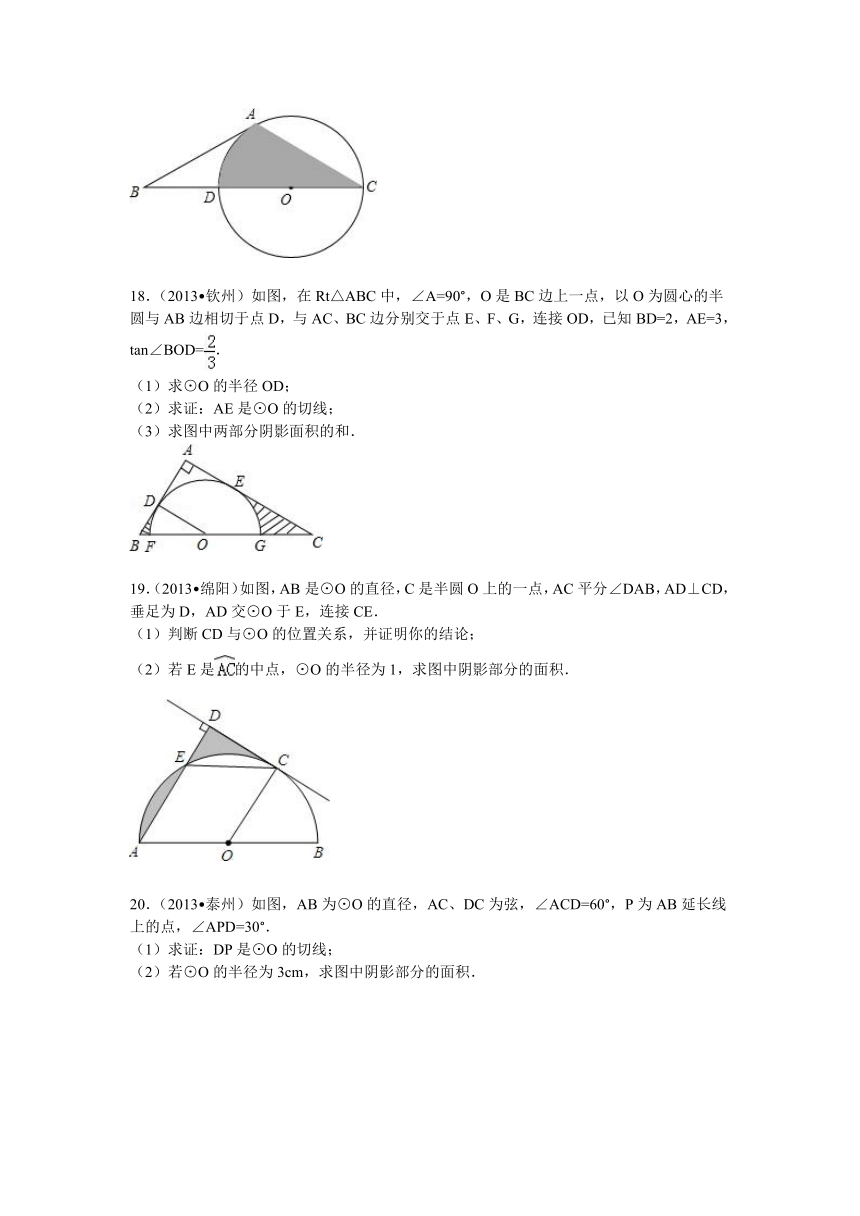
3.(2013 东营)如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa B. 2πa C. D. 3a
4.(2013 德州)如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中阴影部分的面积为( )
A. B. C. D.
5.(2013 赤峰)如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上AD=OA=1,则图中阴影部分的面积为(
A. B. C. D.
6.(2012 泰安)如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则的长为( )
A.π B. 2π C. 3π D. 5π
7.(2013 达州)如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,OF=米,则这段弯路的长度为( )
A. 200π米 B. 100π米 C. 400π米 D. 300π米
8.(2013 遵义)如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( )
A. cm B. (2+π)cm C. cm D. 3cm
二.填空题(共6小题)
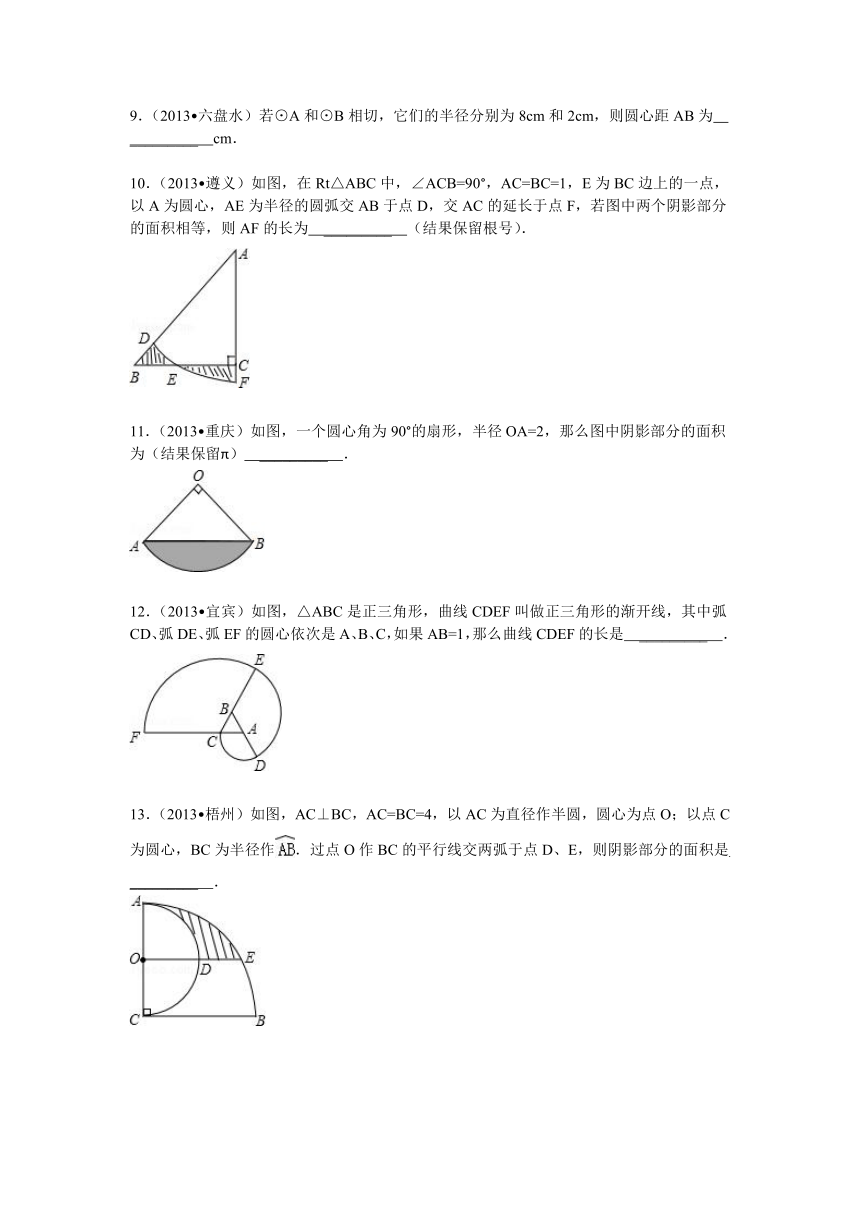
9.(2013 六盘水)若⊙A和⊙B相切,它们的半径分别为8cm和2cm,则圆心距AB为 _________ cm.
10.(2013 遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 _________ (结果保留根号).
11.(2013 重庆)如图,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为(结果保留π) _________ .
12.(2013 宜宾)如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD、弧DE、弧EF的圆心依次是A、B、C,如果AB=1,那么曲线CDEF的长是 _________ .
13.(2013 梧州)如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作.过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 _________ .
14.(2013 济宁)如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 _________ cm.
三.解答题(共8小题)
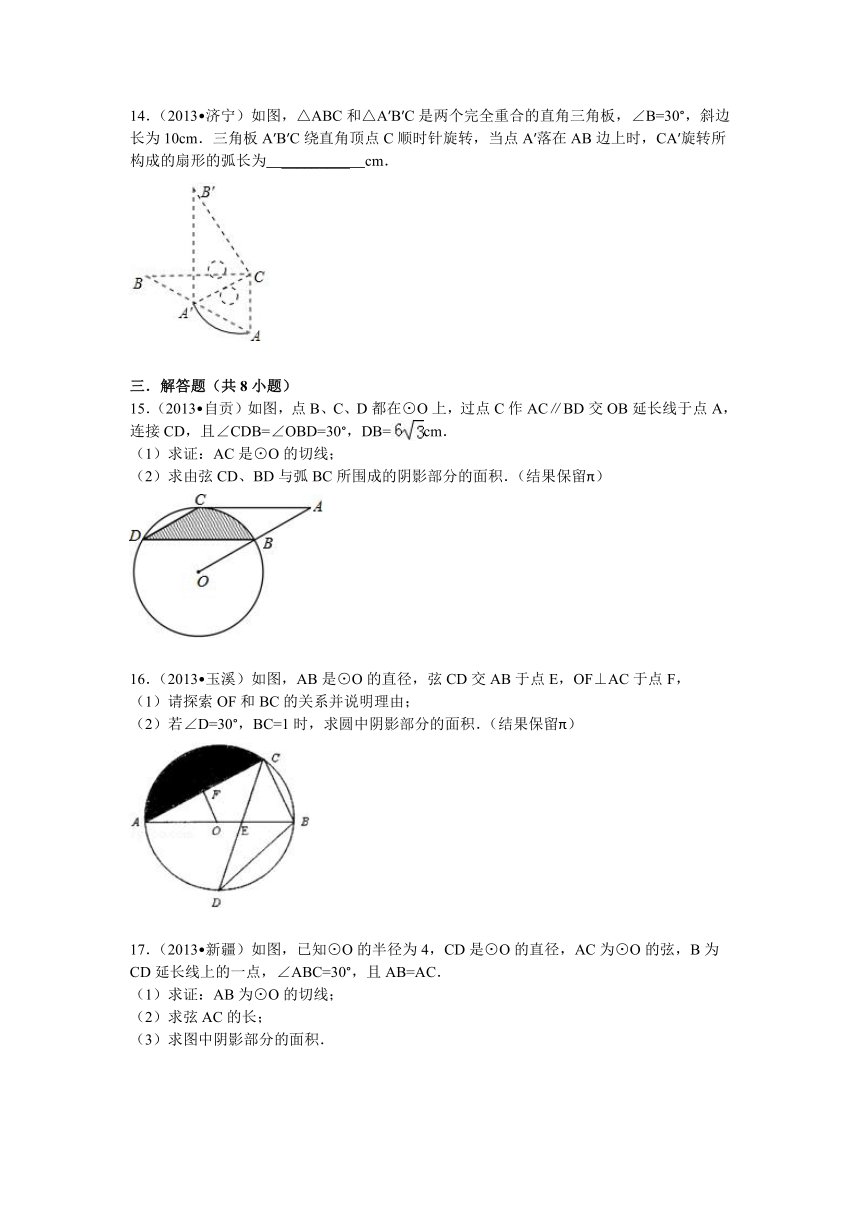
15.(2013 自贡)如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)
16.(2013 玉溪)如图,AB是⊙O的直径,弦CD交AB于点E,OF⊥AC于点F,
(1)请探索OF和BC的关系并说明理由;
(2)若∠D=30°,BC=1时,求圆中阴影部分的面积.(结果保留π)
17.(2013 新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
(1)求证:AB为⊙O的切线;
(2)求弦AC的长;
(3)求图中阴影部分的面积.
18.(2013 钦州)如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
19.(2013 绵阳)如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是的中点,⊙O的半径为1,求图中阴影部分的面积.
20.(2013 泰州)如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
21.(2013 沈阳)如图,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为2的⊙A与OM相切与点B,连接BA并延长交⊙A于点D,交ON于点E.
(1)求证:ON是⊙A的切线;
(2)若∠MON=60°,求图中阴影部分的面积.(结果保留π)
22.(2013 怀化)如图,在△ABC中,∠C=90°,AC+BC=9,点O是斜边AB上一点,以O为圆心2为半径的圆分别与AC、BC相切于点D、E.
(1)求AC、BC的长;
(2)若AC=3,连接BD,求图中阴影部分的面积(π取3.14).
参考答案
一.选择题(共8小题)
1. A.
2. B.
3. A.
4. C.
5. A.
6. B.
7. A.
8. C.
二.填空题(共6小题)
9. 10或6.
10. .
11.π﹣2.
12. 4π.
13. π﹣2.
14. .
三.解答题(共8小题)
15. 如图,连接BC,OD,OC,设OC与BD交于点M.
(1)证明:根据圆周角定理得:∠COB=2∠CDB=2×30°=60°,∵AC∥BD,∴∠A=∠OBD=30°,
∴∠OCA=180°﹣30°﹣60°=90°,即OC⊥AC,∵OC为半径,∴AC是⊙O的切线;
(2)解:由(1)知,AC为⊙O的切线,∴OC⊥AC.∵AC∥BD,∴OC⊥BD.
由垂径定理可知,MD=MB=BD=.
在Rt△OBM中,∠COB=60°,OB===6.
在△CDM与△OBM中,
∴△CDM≌△OBM
∴S△CDM=S△OBM∴阴影部分的面积S阴影=S扇形BOC==6π(cm2).
16.解:(1)OF∥BC,OF=BC.理由:由垂径定理得AF=CF.
∵AO=BO,∴OF是△ABC的中位线.∴OF∥BC,OF=BC.
(2)连接OC.由(1)知OF=.∵AB是⊙O的直径,∴∠ACB=90°.∵∠D=30°,∴∠A=30°.∴AB=2BC=2.∴AC=.
∴S△AOC=×AC×OF=.∵∠AOC=120°,OA=1,
∴S扇形AOC==.∴S阴影=S扇形AOC﹣S△AOC=﹣.
17.(1)证明:如图,连接OA.∵AB=AC,∠ABC=30°,∴∠ABC=∠ACB=30°.∴∠AOB=2∠ACB=60°,∴在△ABO中,∠BAO=180°﹣∠ABO﹣∠AOB=90°,即AB⊥OA,又∵OA是⊙O的半径,∴AB为⊙O的切线;
(2)解:如图,连接AD.∵CD是⊙O的直径,∴∠DAC=90°.∵由(1)知,∠ACB=30°,∴AD=CD=4,
则根据勾股定理知AC==4,即弦AC的长是4;
(3)解:由(2)知,在△ADC中,∠DAC=90°,AD=4,AC=4,则S△ADC=AD AC=×4×4=8.∵点O是△ADC斜边上的中点,∴S△AOC=S△ADC=4.
根据图示知,S阴影=S扇形ADO+S△AOC=+4=+4,即图中阴影部分的面积是+4.
18.解:(1)∵AB与圆O相切,
∴OD⊥AB,在Rt△BDO中,BD=2,tan∠BOD==,∴OD=3;
(2)连接OE,∵AE=OD=3,AE∥OD,∴四边形AEOD为平行四边形,
∴AD∥EO,∵DA⊥AE,∴OE⊥AC,又∵OE为圆的半径,∴AE为圆O的切线;
(3)∵OD∥AC,∴=,即=,∴AC=7.5,∴EC=AC﹣AE=7.5﹣3=4.5,
∴S阴影=S△BDO+S△OEC﹣S扇形FOD﹣S扇形EOG=×2×3+×3×4.5﹣=3+﹣=.
19.解:(1)CD与圆O相切.理由如下:
∵AC为∠DAB的平分线,∴∠DAC=∠BAC,∵OA=OC,∴∠OAC=∠OCA,
∴∠DAC=∠OCA,∴OC∥AD,∵AD⊥CD,∴OC⊥CD,则CD与圆O相切;
(2)连接EB,交OC于F,∵AB为直径,得到∠AEB=90°,
∴EB∥CD,F为EB的中点,∴OF为△ABE的中位线,∴OF=AE=,即CF=DE=,
在Rt△OBF中,根据勾股定理得:EF=FB=DC=,则S阴影=S△DEC=××=.
20.(1)证明:连接OD,∵∠ACD=60°,
∴由圆周角定理得:∠AOD=2∠ACD=120°,∴∠DOP=180°﹣120°=60°,
∵∠APD=30°,∴∠ODP=180°﹣30°﹣60°=90°,∴OD⊥DP,∵OD为半径,∴DP是⊙O切线;
(2)解:∵∠P=30°,∠ODP=90°,OD=3cm,∴OP=6cm,由勾股定理得:DP=3cm,∴图中阴影部分的面积S=S△ODP﹣S扇形DOB=×3×3﹣=(﹣π)cm2
21.(1)证明:过点A作AF⊥ON于点F,
∵⊙A与OM相切与点B,∴AB⊥OM,∵OC平分∠MON,∴AF=AB=2,∴ON是⊙A的切线;
(2)解:∵∠MON=60°,AB⊥OM,∴∠OEB=30°,∴AF⊥ON,∴∠FAE=60°,
在Rt△AEF中,tan∠FAE=,∴EF=AF tan60°=2,∴S阴影=S△AEF﹣S扇形ADF=AF EF﹣×π×AF2=2﹣π.
22.解:(1)连接OD、OE,
∵⊙O切BC于E,切AC于D,∠C=90°,
∴∠ADO=∠BEO=90°,∠ODC=∠C=∠OEC=90°,
∵OE=OD=2,
∴四边形CDOE是正方形,∴CE=CD=OD=OE=2,∠DOE=90°,∵∠OEB=∠C=90°,设AD=x,∵AC+BC=9,∴BE=9﹣2﹣2﹣x=5﹣x,∴OE∥AC,∴∠EOB=∠A,∴△OEB∽△ADO,∴=,∴=,x=1或4,∴AC=3,BC=6或AC=6,BC=3;
(2)∵AC=3,AD=3﹣2=1,BC=6,
∴阴影部分的面积S=S△ACB﹣S△ADB﹣(S正方形CDOE﹣S扇形ODE)=×3×6﹣×1×6﹣(2×2﹣)=9﹣3﹣(4﹣π)=2+π≈5.14.
一.选择题(共8小题)
1.(2013 资阳)钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是( )
A. π B. π C. π D. π
2.(2013 葫芦岛)如图,AB是半圆的直径,AB=2,∠B=30°,则的长为( )
A. B. C. π D.
3.(2013 东营)如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa B. 2πa C. D. 3a
4.(2013 德州)如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中阴影部分的面积为( )
A. B. C. D.
5.(2013 赤峰)如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上AD=OA=1,则图中阴影部分的面积为(
A. B. C. D.
6.(2012 泰安)如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则的长为( )
A.π B. 2π C. 3π D. 5π
7.(2013 达州)如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,OF=米,则这段弯路的长度为( )
A. 200π米 B. 100π米 C. 400π米 D. 300π米
8.(2013 遵义)如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( )
A. cm B. (2+π)cm C. cm D. 3cm
二.填空题(共6小题)
9.(2013 六盘水)若⊙A和⊙B相切,它们的半径分别为8cm和2cm,则圆心距AB为 _________ cm.
10.(2013 遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 _________ (结果保留根号).
11.(2013 重庆)如图,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为(结果保留π) _________ .
12.(2013 宜宾)如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD、弧DE、弧EF的圆心依次是A、B、C,如果AB=1,那么曲线CDEF的长是 _________ .
13.(2013 梧州)如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作.过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 _________ .
14.(2013 济宁)如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 _________ cm.
三.解答题(共8小题)
15.(2013 自贡)如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)
16.(2013 玉溪)如图,AB是⊙O的直径,弦CD交AB于点E,OF⊥AC于点F,
(1)请探索OF和BC的关系并说明理由;
(2)若∠D=30°,BC=1时,求圆中阴影部分的面积.(结果保留π)
17.(2013 新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
(1)求证:AB为⊙O的切线;
(2)求弦AC的长;
(3)求图中阴影部分的面积.
18.(2013 钦州)如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
19.(2013 绵阳)如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是的中点,⊙O的半径为1,求图中阴影部分的面积.
20.(2013 泰州)如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
21.(2013 沈阳)如图,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为2的⊙A与OM相切与点B,连接BA并延长交⊙A于点D,交ON于点E.
(1)求证:ON是⊙A的切线;
(2)若∠MON=60°,求图中阴影部分的面积.(结果保留π)
22.(2013 怀化)如图,在△ABC中,∠C=90°,AC+BC=9,点O是斜边AB上一点,以O为圆心2为半径的圆分别与AC、BC相切于点D、E.
(1)求AC、BC的长;
(2)若AC=3,连接BD,求图中阴影部分的面积(π取3.14).
参考答案
一.选择题(共8小题)
1. A.
2. B.
3. A.
4. C.
5. A.
6. B.
7. A.
8. C.
二.填空题(共6小题)
9. 10或6.
10. .
11.π﹣2.
12. 4π.
13. π﹣2.
14. .
三.解答题(共8小题)
15. 如图,连接BC,OD,OC,设OC与BD交于点M.
(1)证明:根据圆周角定理得:∠COB=2∠CDB=2×30°=60°,∵AC∥BD,∴∠A=∠OBD=30°,
∴∠OCA=180°﹣30°﹣60°=90°,即OC⊥AC,∵OC为半径,∴AC是⊙O的切线;
(2)解:由(1)知,AC为⊙O的切线,∴OC⊥AC.∵AC∥BD,∴OC⊥BD.
由垂径定理可知,MD=MB=BD=.
在Rt△OBM中,∠COB=60°,OB===6.
在△CDM与△OBM中,
∴△CDM≌△OBM
∴S△CDM=S△OBM∴阴影部分的面积S阴影=S扇形BOC==6π(cm2).
16.解:(1)OF∥BC,OF=BC.理由:由垂径定理得AF=CF.
∵AO=BO,∴OF是△ABC的中位线.∴OF∥BC,OF=BC.
(2)连接OC.由(1)知OF=.∵AB是⊙O的直径,∴∠ACB=90°.∵∠D=30°,∴∠A=30°.∴AB=2BC=2.∴AC=.
∴S△AOC=×AC×OF=.∵∠AOC=120°,OA=1,
∴S扇形AOC==.∴S阴影=S扇形AOC﹣S△AOC=﹣.
17.(1)证明:如图,连接OA.∵AB=AC,∠ABC=30°,∴∠ABC=∠ACB=30°.∴∠AOB=2∠ACB=60°,∴在△ABO中,∠BAO=180°﹣∠ABO﹣∠AOB=90°,即AB⊥OA,又∵OA是⊙O的半径,∴AB为⊙O的切线;
(2)解:如图,连接AD.∵CD是⊙O的直径,∴∠DAC=90°.∵由(1)知,∠ACB=30°,∴AD=CD=4,
则根据勾股定理知AC==4,即弦AC的长是4;
(3)解:由(2)知,在△ADC中,∠DAC=90°,AD=4,AC=4,则S△ADC=AD AC=×4×4=8.∵点O是△ADC斜边上的中点,∴S△AOC=S△ADC=4.
根据图示知,S阴影=S扇形ADO+S△AOC=+4=+4,即图中阴影部分的面积是+4.
18.解:(1)∵AB与圆O相切,
∴OD⊥AB,在Rt△BDO中,BD=2,tan∠BOD==,∴OD=3;
(2)连接OE,∵AE=OD=3,AE∥OD,∴四边形AEOD为平行四边形,
∴AD∥EO,∵DA⊥AE,∴OE⊥AC,又∵OE为圆的半径,∴AE为圆O的切线;
(3)∵OD∥AC,∴=,即=,∴AC=7.5,∴EC=AC﹣AE=7.5﹣3=4.5,
∴S阴影=S△BDO+S△OEC﹣S扇形FOD﹣S扇形EOG=×2×3+×3×4.5﹣=3+﹣=.
19.解:(1)CD与圆O相切.理由如下:
∵AC为∠DAB的平分线,∴∠DAC=∠BAC,∵OA=OC,∴∠OAC=∠OCA,
∴∠DAC=∠OCA,∴OC∥AD,∵AD⊥CD,∴OC⊥CD,则CD与圆O相切;
(2)连接EB,交OC于F,∵AB为直径,得到∠AEB=90°,
∴EB∥CD,F为EB的中点,∴OF为△ABE的中位线,∴OF=AE=,即CF=DE=,
在Rt△OBF中,根据勾股定理得:EF=FB=DC=,则S阴影=S△DEC=××=.
20.(1)证明:连接OD,∵∠ACD=60°,
∴由圆周角定理得:∠AOD=2∠ACD=120°,∴∠DOP=180°﹣120°=60°,
∵∠APD=30°,∴∠ODP=180°﹣30°﹣60°=90°,∴OD⊥DP,∵OD为半径,∴DP是⊙O切线;
(2)解:∵∠P=30°,∠ODP=90°,OD=3cm,∴OP=6cm,由勾股定理得:DP=3cm,∴图中阴影部分的面积S=S△ODP﹣S扇形DOB=×3×3﹣=(﹣π)cm2
21.(1)证明:过点A作AF⊥ON于点F,
∵⊙A与OM相切与点B,∴AB⊥OM,∵OC平分∠MON,∴AF=AB=2,∴ON是⊙A的切线;
(2)解:∵∠MON=60°,AB⊥OM,∴∠OEB=30°,∴AF⊥ON,∴∠FAE=60°,
在Rt△AEF中,tan∠FAE=,∴EF=AF tan60°=2,∴S阴影=S△AEF﹣S扇形ADF=AF EF﹣×π×AF2=2﹣π.
22.解:(1)连接OD、OE,
∵⊙O切BC于E,切AC于D,∠C=90°,
∴∠ADO=∠BEO=90°,∠ODC=∠C=∠OEC=90°,
∵OE=OD=2,
∴四边形CDOE是正方形,∴CE=CD=OD=OE=2,∠DOE=90°,∵∠OEB=∠C=90°,设AD=x,∵AC+BC=9,∴BE=9﹣2﹣2﹣x=5﹣x,∴OE∥AC,∴∠EOB=∠A,∴△OEB∽△ADO,∴=,∴=,x=1或4,∴AC=3,BC=6或AC=6,BC=3;
(2)∵AC=3,AD=3﹣2=1,BC=6,
∴阴影部分的面积S=S△ACB﹣S△ADB﹣(S正方形CDOE﹣S扇形ODE)=×3×6﹣×1×6﹣(2×2﹣)=9﹣3﹣(4﹣π)=2+π≈5.14.
