1.5.1 平方差公式(第1课时) 课件(共25张PPT)
文档属性
| 名称 | 1.5.1 平方差公式(第1课时) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 647.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 14:04:08 | ||
图片预览








文档简介
(共25张PPT)
1.5.1平方差公式(第1课时)
第一章
整式的乘除
北师大版七年级下册
学习目标
1.理解并掌握平方差公式的推导和应用.
2.理解平方差公式的结构特征,并能运用公式进行简单的运算.
对于多项式乘以多项式的运算法则你还记得吗?
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘以多项式的法则:
(m+a)(n+b)=mn+mb+an+ab
情境导入
a米
a米
(a-5)米
(a+5)米
小明和小兰分别负责两块区域的值日工作.小明负责一块边长为a米的正方形空地,小兰则负责一块长方形空地,长为正方形空地边长加5米,宽度是正方形空地边长减5米.有一天,小明对小兰说:“咱们换一下值日的区域吧,反正这两块地大小都一样.”你觉得小明说的对吗?为什么?
情境导入
a米
a米
(a-5)米
(a+5)米
答:小明说的不对,长方形面积比正方形面积少了25平方米.
情境导入
探究新知
核心知识点一:
平方差公式
计算下列各题:
(1) (x+2) (x-2); (2) (1+3a) (1-3a );
(3) (x+5y) (x-5y);(4)(2y+z) (2y-z) .
解: (1) (x+2) (x-2)=x2-22 (2) (1+3a) (1-3a )=12-(3a)2
(3) (x+5y) (x-5y)=x2-(5y)2 (4) (2y+z) (2y-z)=(2y)2-z2
上述问题中,相乘的两个多项式有什么特点?它们相乘的结果有什么规律?
(1)都是乘积的形式.
(2)这两个多项式都有两项,它们有两个数是完全相同的,有两个数是相反的.
(3)结果是这两项的平方差,而且是同号的平方减异号的平方.
这就是我们今天要学习的一个重要公式:平方差公式
探究新知
归纳总结
(1)平方差公式的推导:(a+b)(a-b)= =
.
(2)文字语言:两个数的和与这两个数的差的积,等于
这两个数的 .
(3)符号语言:(a+b)(a-b)= .
a2-ab+ab-b2
a2-b2
平方差
a2-b2
平方差公式:
探究新知
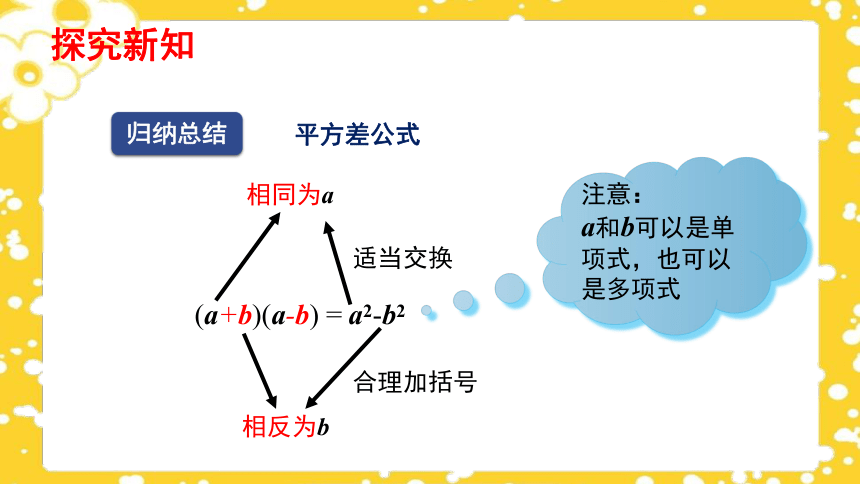
平方差公式
相同为a
相反为b
适当交换
合理加括号
注意:
a和b可以是单项式,也可以是多项式
(a+b)(a-b) = a2-b2
归纳总结
探究新知
(a+b)(a b)=a2 b2
结构特点:
(1) 公式左边两个二项式必须是相同两数的和与差相乘;且左边两括号内的第一项相等、第二项符号相反[互为相反数(式)];
(2) 公式右边是这两个数的平方差;即右边是左边括号内的第一项的平方减去第二项的平方.
(3) 公式中的 a和b 可以代表数,也可以是代数式.
归纳总结
探究新知
例题讲解
例1 : 利用平方差公式计算:
(1) (5+6x)(5-6x);(2) (x-2y)(x+2y);
(3) (-m+n)(-m-n) .
解:(1) (5+6x)(5-6x)= 52-(6x)2=25-36x2;
(2) (x-2y)(x+2y)= x2-(2y)2= x2-4y2 ;
(3) (-m+n)(-m-n) = (-m)2-n2 = m2-n2 .
平方差公式中的a,b可以是单项式也可以为多项式。
( x + y+z)( x + y – z).
= ( x + y)2 – z2
解: 原式=[( x + y) + z][( x + y) – z]
例2:利用平方差公式计算:
例题讲解
当 m = 2 时,原式 = 24 – 16 = 0
= m4 – 16
= (m2 – 4)(m2 + 4)
=(m + 2)(m – 2)(m2 + 4)
解:(1) (m + 2)(m2 + 4)(m – 2)
例3 : 先化简,再求值 :
(m + 2)(m2 + 4)(m – 2),其中m = 2.
例题讲解
方法总结:利用平方差公式先化简再求值,
切忌代入数值直接计算.
例4 :先化简,再求值:(2x-y)(y+2x)-(2y+
x)(2y-x),其中x=1,y=2.
解:(2x-y)(y+2x)-(2y+x)(2y-x)
=4x2-y2- (4y2-x2)
=4x2-y2-4y2+x2=5x2-5y2.
当x=1,y=2时,原式=5×12-5×22=-15.
例题讲解
随堂练习
1. 下列计算正确的是( )
A. (x2+3)(x2-3)=x2-9
B. (x+3)(x-2)=x2-6
C. (3x+2)(3x-2)=3x2-4
D. (-x+y)(-x-y)=x2-y2
D
2. 若a2-b2=- ,a+b=- ,则a-b的值为 ( )
A. B.
C. 2 D. 4
3. 用平方差公式计算(x-1)(x+1)(x2+1)结果正确的是 ( )
A. x4-1 B. x4+1
C.(x-1)4 D.(x+1)4
A
A
随堂练习
4. 下列式子不能用平方差公式计算的是( )
A. (m+n)(m-n) B. (m-n)(-m-n)
C. (m-n)(-m+n) D. (n-m)(-m-n)
5. 下列各式计算正确的是( )
A. 2a2+3a2=5a4 B.(-2ab)3=-6ab3
C.(3a+b)(3a-b)=9a2-b2 D. a3·(-2a)=-2a3
C
C
随堂练习
6. 已知a+b=53,a-b=38,则a2-b2的值为 ( )
A. 15 B. 38 C. 53 D. 2 014
D
7. 下列各式计算正确的是( )
A. 2a2+3a2=5a4
B.(-2ab)3=-6ab3
C.(3a+b)(3a-b)=9a2-b2
D. a3·(-2a)=-2a3
C
随堂练习
8. 计算:
(1)(x+6)(x-6)=________;
(2)(2+a)(2-a)=________ ;
(3)(x+2y)(x-2y)=________ ;
(4)(2m-5n)(2m+5n)=________.
4m2-25n2
x2-36
4-a2
x2-4y2
随堂练习
9. 计算:
(1)(x+3)(x-3);
(2)(a+b)(a-b).
解: 原式=x2-3x+3x-9=x2-9
解: 原式=a2-ab+ab-b2=a2-b2
随堂练习
9.计算:
(3)(x+2)(x-2);
(4)(m-1)(m+1).
解: 原式=x2-22=x2-4
解:原式=m2-12=m2-1
随堂练习
9. 计算:
(5)(a+4)(a-4);
(6)(x-5)(x+5).
解: 原式=a2-42=a2-16
解:原式=x2-52=x2-25
随堂练习
9.计算:
(7)(3x+2)(3x-2);
(8)(3x+2y)(3x-2y).
解: 原式=(3x)2-22=9x2-4
解:原式=(3x)2-(2y)2=9x2-4y2
随堂练习
9.计算:
(9)(-m+n)(-m-n);
(10)(2+m)(-2+m).
解: 原式=(-m)2-n2=m2-n2
解:原式=(m+2)(m-2)=m2-22=m2-4
随堂练习
课堂小结
1、平方差公式 :
(a+b)(a b)= a2 b2.
2、应用平方差公式时要注意一些什么?
(1)运用平方差公式时,要紧扣公式的特征,找出符号相等的“项”和符号相反的“项”,然后应用公式.
(2)对于不符合平方差公式的标准形式者,要利用加法交换律交换位置,或者提取两个“ ”号中的“ ”号,变成公式的标准形式后,再运用公式.
1.5.1平方差公式(第1课时)
第一章
整式的乘除
北师大版七年级下册
学习目标
1.理解并掌握平方差公式的推导和应用.
2.理解平方差公式的结构特征,并能运用公式进行简单的运算.
对于多项式乘以多项式的运算法则你还记得吗?
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘以多项式的法则:
(m+a)(n+b)=mn+mb+an+ab
情境导入
a米
a米
(a-5)米
(a+5)米
小明和小兰分别负责两块区域的值日工作.小明负责一块边长为a米的正方形空地,小兰则负责一块长方形空地,长为正方形空地边长加5米,宽度是正方形空地边长减5米.有一天,小明对小兰说:“咱们换一下值日的区域吧,反正这两块地大小都一样.”你觉得小明说的对吗?为什么?
情境导入
a米
a米
(a-5)米
(a+5)米
答:小明说的不对,长方形面积比正方形面积少了25平方米.
情境导入
探究新知
核心知识点一:
平方差公式
计算下列各题:
(1) (x+2) (x-2); (2) (1+3a) (1-3a );
(3) (x+5y) (x-5y);(4)(2y+z) (2y-z) .
解: (1) (x+2) (x-2)=x2-22 (2) (1+3a) (1-3a )=12-(3a)2
(3) (x+5y) (x-5y)=x2-(5y)2 (4) (2y+z) (2y-z)=(2y)2-z2
上述问题中,相乘的两个多项式有什么特点?它们相乘的结果有什么规律?
(1)都是乘积的形式.
(2)这两个多项式都有两项,它们有两个数是完全相同的,有两个数是相反的.
(3)结果是这两项的平方差,而且是同号的平方减异号的平方.
这就是我们今天要学习的一个重要公式:平方差公式
探究新知
归纳总结
(1)平方差公式的推导:(a+b)(a-b)= =
.
(2)文字语言:两个数的和与这两个数的差的积,等于
这两个数的 .
(3)符号语言:(a+b)(a-b)= .
a2-ab+ab-b2
a2-b2
平方差
a2-b2
平方差公式:
探究新知
平方差公式
相同为a
相反为b
适当交换
合理加括号
注意:
a和b可以是单项式,也可以是多项式
(a+b)(a-b) = a2-b2
归纳总结
探究新知
(a+b)(a b)=a2 b2
结构特点:
(1) 公式左边两个二项式必须是相同两数的和与差相乘;且左边两括号内的第一项相等、第二项符号相反[互为相反数(式)];
(2) 公式右边是这两个数的平方差;即右边是左边括号内的第一项的平方减去第二项的平方.
(3) 公式中的 a和b 可以代表数,也可以是代数式.
归纳总结
探究新知
例题讲解
例1 : 利用平方差公式计算:
(1) (5+6x)(5-6x);(2) (x-2y)(x+2y);
(3) (-m+n)(-m-n) .
解:(1) (5+6x)(5-6x)= 52-(6x)2=25-36x2;
(2) (x-2y)(x+2y)= x2-(2y)2= x2-4y2 ;
(3) (-m+n)(-m-n) = (-m)2-n2 = m2-n2 .
平方差公式中的a,b可以是单项式也可以为多项式。
( x + y+z)( x + y – z).
= ( x + y)2 – z2
解: 原式=[( x + y) + z][( x + y) – z]
例2:利用平方差公式计算:
例题讲解
当 m = 2 时,原式 = 24 – 16 = 0
= m4 – 16
= (m2 – 4)(m2 + 4)
=(m + 2)(m – 2)(m2 + 4)
解:(1) (m + 2)(m2 + 4)(m – 2)
例3 : 先化简,再求值 :
(m + 2)(m2 + 4)(m – 2),其中m = 2.
例题讲解
方法总结:利用平方差公式先化简再求值,
切忌代入数值直接计算.
例4 :先化简,再求值:(2x-y)(y+2x)-(2y+
x)(2y-x),其中x=1,y=2.
解:(2x-y)(y+2x)-(2y+x)(2y-x)
=4x2-y2- (4y2-x2)
=4x2-y2-4y2+x2=5x2-5y2.
当x=1,y=2时,原式=5×12-5×22=-15.
例题讲解
随堂练习
1. 下列计算正确的是( )
A. (x2+3)(x2-3)=x2-9
B. (x+3)(x-2)=x2-6
C. (3x+2)(3x-2)=3x2-4
D. (-x+y)(-x-y)=x2-y2
D
2. 若a2-b2=- ,a+b=- ,则a-b的值为 ( )
A. B.
C. 2 D. 4
3. 用平方差公式计算(x-1)(x+1)(x2+1)结果正确的是 ( )
A. x4-1 B. x4+1
C.(x-1)4 D.(x+1)4
A
A
随堂练习
4. 下列式子不能用平方差公式计算的是( )
A. (m+n)(m-n) B. (m-n)(-m-n)
C. (m-n)(-m+n) D. (n-m)(-m-n)
5. 下列各式计算正确的是( )
A. 2a2+3a2=5a4 B.(-2ab)3=-6ab3
C.(3a+b)(3a-b)=9a2-b2 D. a3·(-2a)=-2a3
C
C
随堂练习
6. 已知a+b=53,a-b=38,则a2-b2的值为 ( )
A. 15 B. 38 C. 53 D. 2 014
D
7. 下列各式计算正确的是( )
A. 2a2+3a2=5a4
B.(-2ab)3=-6ab3
C.(3a+b)(3a-b)=9a2-b2
D. a3·(-2a)=-2a3
C
随堂练习
8. 计算:
(1)(x+6)(x-6)=________;
(2)(2+a)(2-a)=________ ;
(3)(x+2y)(x-2y)=________ ;
(4)(2m-5n)(2m+5n)=________.
4m2-25n2
x2-36
4-a2
x2-4y2
随堂练习
9. 计算:
(1)(x+3)(x-3);
(2)(a+b)(a-b).
解: 原式=x2-3x+3x-9=x2-9
解: 原式=a2-ab+ab-b2=a2-b2
随堂练习
9.计算:
(3)(x+2)(x-2);
(4)(m-1)(m+1).
解: 原式=x2-22=x2-4
解:原式=m2-12=m2-1
随堂练习
9. 计算:
(5)(a+4)(a-4);
(6)(x-5)(x+5).
解: 原式=a2-42=a2-16
解:原式=x2-52=x2-25
随堂练习
9.计算:
(7)(3x+2)(3x-2);
(8)(3x+2y)(3x-2y).
解: 原式=(3x)2-22=9x2-4
解:原式=(3x)2-(2y)2=9x2-4y2
随堂练习
9.计算:
(9)(-m+n)(-m-n);
(10)(2+m)(-2+m).
解: 原式=(-m)2-n2=m2-n2
解:原式=(m+2)(m-2)=m2-22=m2-4
随堂练习
课堂小结
1、平方差公式 :
(a+b)(a b)= a2 b2.
2、应用平方差公式时要注意一些什么?
(1)运用平方差公式时,要紧扣公式的特征,找出符号相等的“项”和符号相反的“项”,然后应用公式.
(2)对于不符合平方差公式的标准形式者,要利用加法交换律交换位置,或者提取两个“ ”号中的“ ”号,变成公式的标准形式后,再运用公式.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
