2022—2023学年北师大版数学九年级下册1.1 锐角三角函数 同步练习(无答案)
文档属性
| 名称 | 2022—2023学年北师大版数学九年级下册1.1 锐角三角函数 同步练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 501.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 15:46:57 | ||
图片预览

文档简介
锐角三角函数
选择题
1、如图,点、、都在格点上,则的正弦值是( )
A. B. C. D.
2、如图,等腰Rt△ABC中,∠A=90°,AB=AC,BD为△ABC的角平分线,若,则的长为( )
A.3 B. C.4 D.
3、如图,与,,分别交于点E,G,F,且,,则下列结论错误的是( )
A. B. C. D.
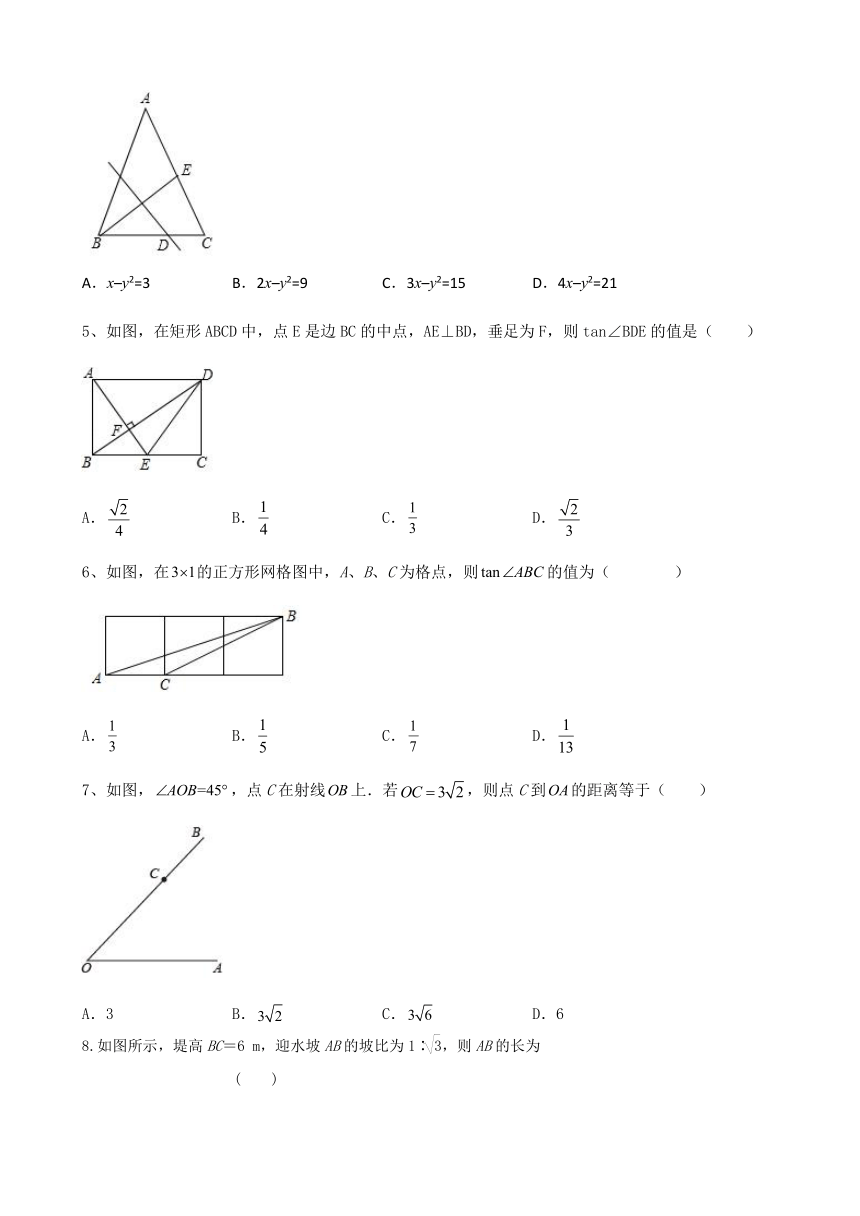
4、如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
A.x–y2=3 B.2x–y2=9 C.3x–y2=15 D.4x–y2=21
5、如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A. B. C. D.
6、如图,在的正方形网格图中,A、B、C为格点,则的值为( )
A. B. C. D.
7、如图,,点C在射线上.若,则点C到的距离等于( )
A.3 B. C. D.6
8.如图所示,堤高BC=6 m,迎水坡AB的坡比为1∶,则AB的长为 ( )
A.12 m B.4 m
C.5 m D.6 m
填空题
1如图,已知在Rt△ABC中,∠ACB=90°,AC=1,AB=2,则sinB的值是 .
2、如图,在等腰ABO中,AO=AB,OB=6,以OB为半径作⊙O交AB于点C,若BC=4,则cosA=_______
3、已知某斜坡的坡度,则斜坡的坡角的大小为_________.
4、阅读材料:余弦定理是描述三角形中三边长度与一个角的余弦值关系的定理,是勾股定理在一般三角形情形下的推广.对于任意三角形,任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍.定理解读:如图,在任意中,以边为例,其它两边是和,和的夹角为,根据余弦定理有,类似的可以得到关于和的关系式.已知在中,,,是和的比例中项,那么的余弦值为____.
5如图所示的网格是正方形网格,则tan α+tan β= .
解答题
1.在△ABC,∠C=90°,BC=2,AB=5,求sinA,cosA,tanA.
2、如图所示,△ABC中,D为AB的中点,DC⊥AC,且∠BCD=30°,求∠CDA的正弦值、余弦值、正切值和余切值.
3、如图,直线分别与轴、轴交于点,,点,与反比例函数交于点,,点在直线上,且,为的中点.
(1)求反比例函数的解析式;
(2)连接,求的值.
4、如图,在由边长为1个单位长度的小正方形组成的10×10网格中,线段AB的端点A、B均为网格线的交点.
(1)将线段AB先向上平移4个单位长度,再向右平移3个单位长度得到线段A1B1,画出线段A1B1;
(2)将线段A1B1绕点A1顺时针旋转90°得到线段A1B2,画出线段A1B2;
(3)连接BB1,直接写出sin∠B1BA=_____.
5、图,在直角坐标系中,直线与双曲线分别相交于第二、四象限内的,两点,与x轴相交于C点,与y轴相交于D点.已知,.
(1)点C坐标是______,点D坐标是______;
(2)求,对应的函数表达式;
(3)求的面积.
选择题
1、如图,点、、都在格点上,则的正弦值是( )
A. B. C. D.
2、如图,等腰Rt△ABC中,∠A=90°,AB=AC,BD为△ABC的角平分线,若,则的长为( )
A.3 B. C.4 D.
3、如图,与,,分别交于点E,G,F,且,,则下列结论错误的是( )
A. B. C. D.
4、如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
A.x–y2=3 B.2x–y2=9 C.3x–y2=15 D.4x–y2=21
5、如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A. B. C. D.
6、如图,在的正方形网格图中,A、B、C为格点,则的值为( )
A. B. C. D.
7、如图,,点C在射线上.若,则点C到的距离等于( )
A.3 B. C. D.6
8.如图所示,堤高BC=6 m,迎水坡AB的坡比为1∶,则AB的长为 ( )
A.12 m B.4 m
C.5 m D.6 m
填空题
1如图,已知在Rt△ABC中,∠ACB=90°,AC=1,AB=2,则sinB的值是 .
2、如图,在等腰ABO中,AO=AB,OB=6,以OB为半径作⊙O交AB于点C,若BC=4,则cosA=_______
3、已知某斜坡的坡度,则斜坡的坡角的大小为_________.
4、阅读材料:余弦定理是描述三角形中三边长度与一个角的余弦值关系的定理,是勾股定理在一般三角形情形下的推广.对于任意三角形,任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍.定理解读:如图,在任意中,以边为例,其它两边是和,和的夹角为,根据余弦定理有,类似的可以得到关于和的关系式.已知在中,,,是和的比例中项,那么的余弦值为____.
5如图所示的网格是正方形网格,则tan α+tan β= .
解答题
1.在△ABC,∠C=90°,BC=2,AB=5,求sinA,cosA,tanA.
2、如图所示,△ABC中,D为AB的中点,DC⊥AC,且∠BCD=30°,求∠CDA的正弦值、余弦值、正切值和余切值.
3、如图,直线分别与轴、轴交于点,,点,与反比例函数交于点,,点在直线上,且,为的中点.
(1)求反比例函数的解析式;
(2)连接,求的值.
4、如图,在由边长为1个单位长度的小正方形组成的10×10网格中,线段AB的端点A、B均为网格线的交点.
(1)将线段AB先向上平移4个单位长度,再向右平移3个单位长度得到线段A1B1,画出线段A1B1;
(2)将线段A1B1绕点A1顺时针旋转90°得到线段A1B2,画出线段A1B2;
(3)连接BB1,直接写出sin∠B1BA=_____.
5、图,在直角坐标系中,直线与双曲线分别相交于第二、四象限内的,两点,与x轴相交于C点,与y轴相交于D点.已知,.
(1)点C坐标是______,点D坐标是______;
(2)求,对应的函数表达式;
(3)求的面积.
