5.4.2正弦函数、余弦函数性质第2课时 课件(共24张PPT)
文档属性
| 名称 | 5.4.2正弦函数、余弦函数性质第2课时 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 995.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 21:01:02 | ||
图片预览







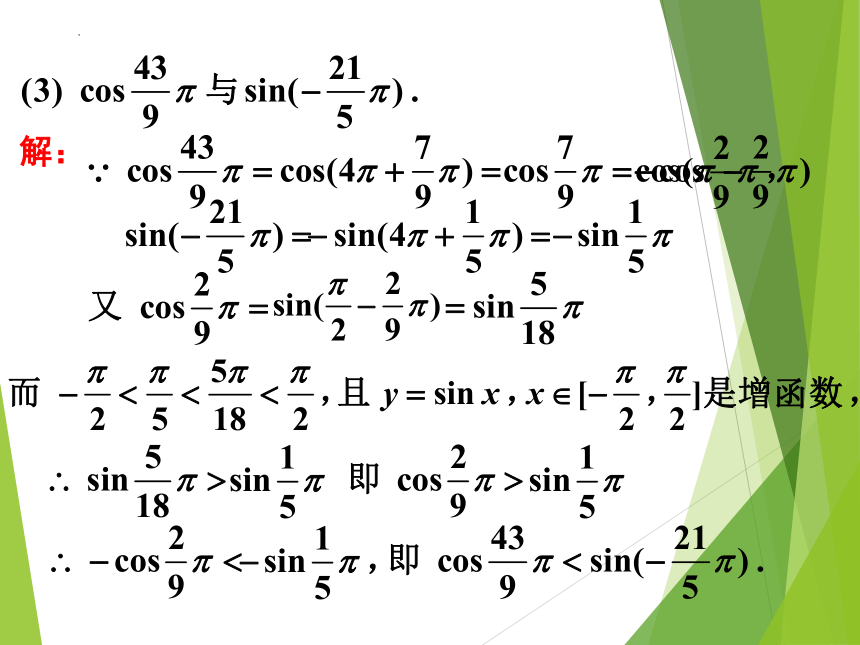
文档简介
(共24张PPT)
第2课时
5.4.2 正弦函数、余弦函数
的性质
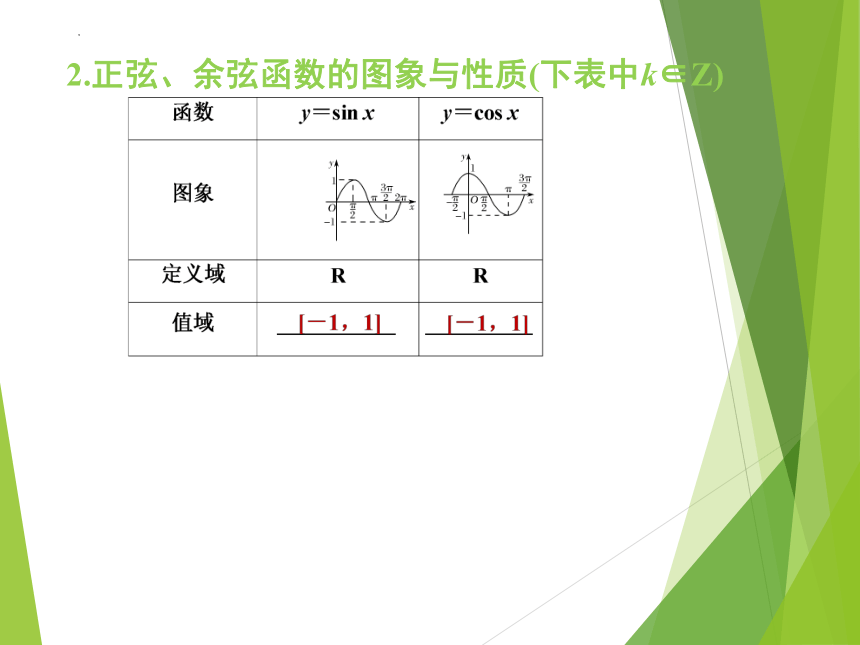
2.正弦、余弦函数的图象与性质(下表中k∈Z)
2.正弦、余弦函数的图象与性质(下表中k∈Z)
一般结论:
例1.求下列函数的最大值,并求出最大值时x的集合:
解:
y 取得最大值
∴函数的最大值为2,取最大值时的x集合为
y 取得最大值
∴函数的最大值为1,取最大值时的x集合为
探究应用1:最值
解:
函数取得最大值
.
此时函数为常数函数,
函数取得最大值
①
②
③
函数最大值
注意:对于含参数的最大值或最小值问题,要对
或 的系数进行讨论.
思考:此例若改为求最小值,结果如何?
例2 比较下列各组数的大小:
解:
探究应用2:比较大小
解:
解:
由复合函数“同增异减”原则知,
例3.
探究应用3:单调性
函数y=3sin(
-2x)在什么区间是单调递减
解:∵y=3sin(
-2x)=-3sin(2x-
)
由2kπ-
≤2x
得kπ-
≤x≤kπ+
(k∈Z)为所求.
或:令u=
-2x,则u是x的减函数
又∵y=sinu在[2kπ-
,2kπ+
](k∈Z)上为增函数,
∴原函数y=3sin(
-2x)在区间[2kπ-
,2kπ+
]上递减.
设2kπ-
≤
-2x≤2kπ+
解得kπ-
≤x≤kπ+
(k∈Z)
∴原函数y=3sin(
-2x)在[kπ-
,kπ+
](k∈Z)上单调递减.
变式1
变式2
解:令
则
因为
的单调递增区间是
,且由
得
所以,函数
的单调递增区间是
例4.
增区间
减区间
∵ y=sinx 的单调区间为:
单调增、减区间由下面不等式确定:
解得:
备选例题
总结升华
1.正余弦函数的图象和性质
课后作业
教材P207练习T1-5
P213习题5.4T4,T5,T16
第2课时
5.4.2 正弦函数、余弦函数
的性质
2.正弦、余弦函数的图象与性质(下表中k∈Z)
2.正弦、余弦函数的图象与性质(下表中k∈Z)
一般结论:
例1.求下列函数的最大值,并求出最大值时x的集合:
解:
y 取得最大值
∴函数的最大值为2,取最大值时的x集合为
y 取得最大值
∴函数的最大值为1,取最大值时的x集合为
探究应用1:最值
解:
函数取得最大值
.
此时函数为常数函数,
函数取得最大值
①
②
③
函数最大值
注意:对于含参数的最大值或最小值问题,要对
或 的系数进行讨论.
思考:此例若改为求最小值,结果如何?
例2 比较下列各组数的大小:
解:
探究应用2:比较大小
解:
解:
由复合函数“同增异减”原则知,
例3.
探究应用3:单调性
函数y=3sin(
-2x)在什么区间是单调递减
解:∵y=3sin(
-2x)=-3sin(2x-
)
由2kπ-
≤2x
得kπ-
≤x≤kπ+
(k∈Z)为所求.
或:令u=
-2x,则u是x的减函数
又∵y=sinu在[2kπ-
,2kπ+
](k∈Z)上为增函数,
∴原函数y=3sin(
-2x)在区间[2kπ-
,2kπ+
]上递减.
设2kπ-
≤
-2x≤2kπ+
解得kπ-
≤x≤kπ+
(k∈Z)
∴原函数y=3sin(
-2x)在[kπ-
,kπ+
](k∈Z)上单调递减.
变式1
变式2
解:令
则
因为
的单调递增区间是
,且由
得
所以,函数
的单调递增区间是
例4.
增区间
减区间
∵ y=sinx 的单调区间为:
单调增、减区间由下面不等式确定:
解得:
备选例题
总结升华
1.正余弦函数的图象和性质
课后作业
教材P207练习T1-5
P213习题5.4T4,T5,T16
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
