6.2.1向量的加法运算 课件(共24张PPT)
文档属性
| 名称 | 6.2.1向量的加法运算 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 21:06:20 | ||
图片预览







文档简介
(共24张PPT)
6.2.1 向量的加法运算
1.理解并掌握向量加法的概念,了解向量加法的几何意义及其运算律;
2.会用向量的三角形法则和平行四边形法则求两个向量的和;
3.能够利用向量的交换律和结合律进行向量运算.
学习目标
理解并掌握向量加法的三角形法则和平行四边形法则
重点:
难点:
向量加法的几何意义及运算律
直尺、双色笔、练习本、笔记本
工具准备:
3、两个特殊的向量
1、向量的概念
既有大小,又有方向的量叫做向量.
平行向量:方向相同或相反的向量
相等向量:方向相同,长度相等的两个向量叫做相等向量.
A
B
表示方法:(1)有向线段
2、向量的表示方法及向量的模?
(2)字母表示 ,
知识回顾:
零向量 单位向量
4、平行向量(共线向量),相等向量
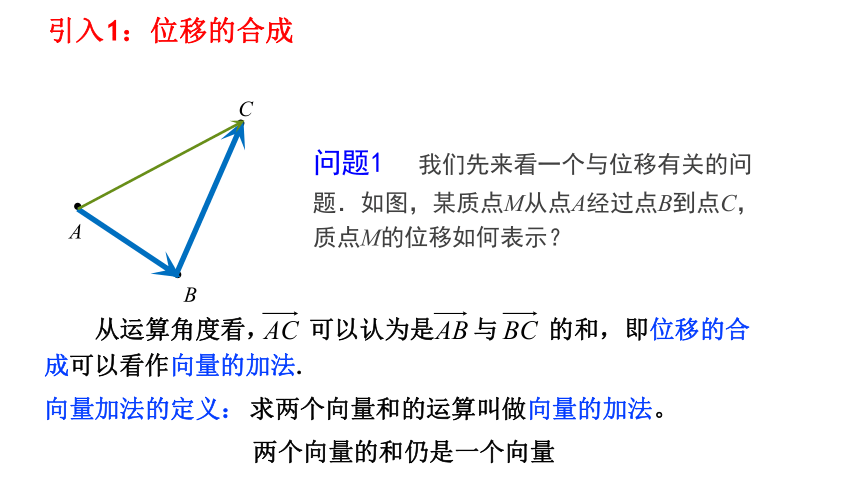
引入1:位移的合成
从运算角度看, 可以认为是 与 的和,即位移的合成可以看作向量的加法.
向量加法的定义:
两个向量的和仍是一个向量
求两个向量和的运算叫做向量的加法。
A
B
C
问题1 我们先来看一个与位移有关的问题.如图,某质点M从点A经过点B到点C,质点M的位移如何表示?
如图,已知向量 ,求作向量 。
向量加法的三角形法则
首尾相连,连首尾
位移的合成可以看作向量加法三角形法则的物理模型。
在平面内任取一点O,
①
作 , ,
②
则向量 叫做 和 的和,记作 .
即
③
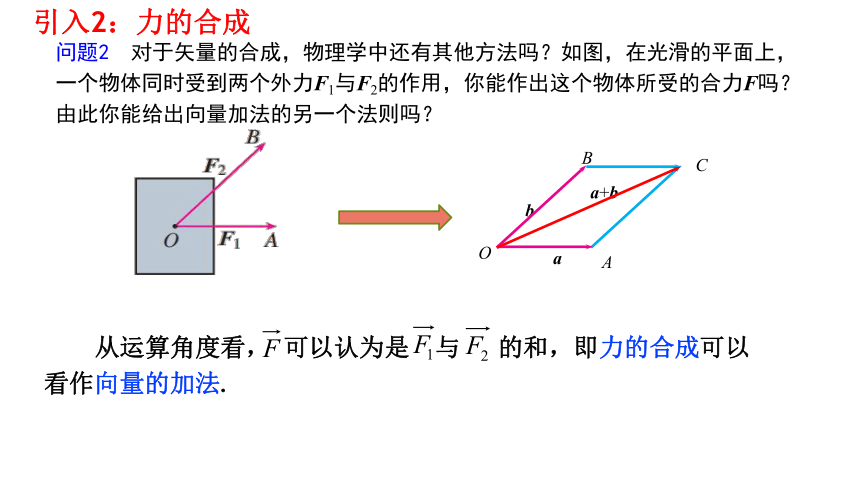
问题2 对于矢量的合成,物理学中还有其他方法吗?如图,在光滑的平面上,一个物体同时受到两个外力F1与F2的作用,你能作出这个物体所受的合力F吗?由此你能给出向量加法的另一个法则吗?
B
O
A
a
b
C
a+b
从运算角度看, 可以认为是 与 的和,即力的合成可以看作向量的加法.
引入2:力的合成
如图,已知向量 ,求作向量 。
①在平面内任取一点O,
②作 , ,
③以 为邻边作 ,
连结OC,则
向量加法的平行四边形法则
共起点,对角线为和
力的合成可以看作向量加法平行四边形法则的物理模型。
思考:向量的平行四边形法则与三角形法则一致吗?为什么?
a
b
b
a
a
b
例1: 如图,已知向量 ,作出
a
b
a
b
b
B
a
O
A
a
O
A
b
B
思考:
(1)
(2)
(3)
加法交换律:
加法结合律:
O
C
B
A
向量的加法的运算律
B
D
A
C
例2 长江两岸之间没有大桥的地方,常常通过轮船进行运输,如图,一艘船从长江南岸A点出发,垂直于对岸航行,航行速度的大小为6 km/h,同时江水的速度为向东6km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹角来表示)。
A
D
B
C
解(1):如图,表示船速,表示江水速度,以为邻边作□,则表示船实际航行的速度.
课堂小结
1、向量加法的三角形法则
(首尾相连,起点指向终点)
2、向量加法的平行四边形法则
3、向量形式的不等式
4、向量加法的运算律
交换律:
结合律:
(起点相同,对角线为和)
作业:课时作业(2)
随堂练习
6.2.1 向量的加法运算
1.理解并掌握向量加法的概念,了解向量加法的几何意义及其运算律;
2.会用向量的三角形法则和平行四边形法则求两个向量的和;
3.能够利用向量的交换律和结合律进行向量运算.
学习目标
理解并掌握向量加法的三角形法则和平行四边形法则
重点:
难点:
向量加法的几何意义及运算律
直尺、双色笔、练习本、笔记本
工具准备:
3、两个特殊的向量
1、向量的概念
既有大小,又有方向的量叫做向量.
平行向量:方向相同或相反的向量
相等向量:方向相同,长度相等的两个向量叫做相等向量.
A
B
表示方法:(1)有向线段
2、向量的表示方法及向量的模?
(2)字母表示 ,
知识回顾:
零向量 单位向量
4、平行向量(共线向量),相等向量
引入1:位移的合成
从运算角度看, 可以认为是 与 的和,即位移的合成可以看作向量的加法.
向量加法的定义:
两个向量的和仍是一个向量
求两个向量和的运算叫做向量的加法。
A
B
C
问题1 我们先来看一个与位移有关的问题.如图,某质点M从点A经过点B到点C,质点M的位移如何表示?
如图,已知向量 ,求作向量 。
向量加法的三角形法则
首尾相连,连首尾
位移的合成可以看作向量加法三角形法则的物理模型。
在平面内任取一点O,
①
作 , ,
②
则向量 叫做 和 的和,记作 .
即
③
问题2 对于矢量的合成,物理学中还有其他方法吗?如图,在光滑的平面上,一个物体同时受到两个外力F1与F2的作用,你能作出这个物体所受的合力F吗?由此你能给出向量加法的另一个法则吗?
B
O
A
a
b
C
a+b
从运算角度看, 可以认为是 与 的和,即力的合成可以看作向量的加法.
引入2:力的合成
如图,已知向量 ,求作向量 。
①在平面内任取一点O,
②作 , ,
③以 为邻边作 ,
连结OC,则
向量加法的平行四边形法则
共起点,对角线为和
力的合成可以看作向量加法平行四边形法则的物理模型。
思考:向量的平行四边形法则与三角形法则一致吗?为什么?
a
b
b
a
a
b
例1: 如图,已知向量 ,作出
a
b
a
b
b
B
a
O
A
a
O
A
b
B
思考:
(1)
(2)
(3)
加法交换律:
加法结合律:
O
C
B
A
向量的加法的运算律
B
D
A
C
例2 长江两岸之间没有大桥的地方,常常通过轮船进行运输,如图,一艘船从长江南岸A点出发,垂直于对岸航行,航行速度的大小为6 km/h,同时江水的速度为向东6km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹角来表示)。
A
D
B
C
解(1):如图,表示船速,表示江水速度,以为邻边作□,则表示船实际航行的速度.
课堂小结
1、向量加法的三角形法则
(首尾相连,起点指向终点)
2、向量加法的平行四边形法则
3、向量形式的不等式
4、向量加法的运算律
交换律:
结合律:
(起点相同,对角线为和)
作业:课时作业(2)
随堂练习
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
