2.2基本不等式 课件(共16张PPT)
文档属性
| 名称 | 2.2基本不等式 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-15 21:08:49 | ||
图片预览





文档简介
第二章 一元二次函数、方程和不等式
2.2 基本不等式
动手试试看!
先将两张正方形纸沿对角线折成两个等腰直角三角形,再用这两个三角形拼接构造出一个矩形(两边分别等于两个等腰直角三角形的直角边,多余部分折叠)。设这两个正方形的面积分别为a和b,观察两个三角形的面积和矩形面积,你发现了什么?
如果a>0,b>0,我们用 分别代替上式中的a,b,可得到:
由上式可得:
(当且仅当a=b时,等号成立)
? a, b∈R,有a2+b2 ≥ 2ab (当且仅当a=b时,等号成立)
通常称上述不等式为基本不等式.
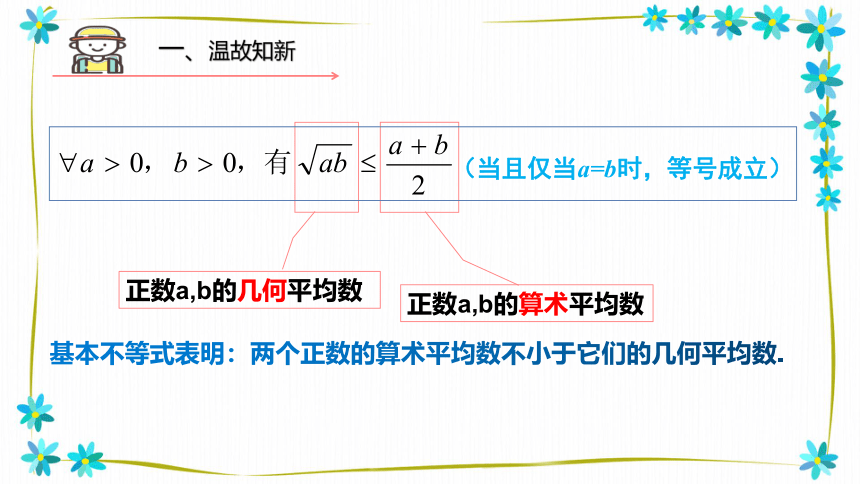
一、温故知新
正数a,b的算术平均数
正数a,b的几何平均数
基本不等式表明:两个正数的算术平均数不小于它们的几何平均数.
一、温故知新
(当且仅当a=b时,等号成立)
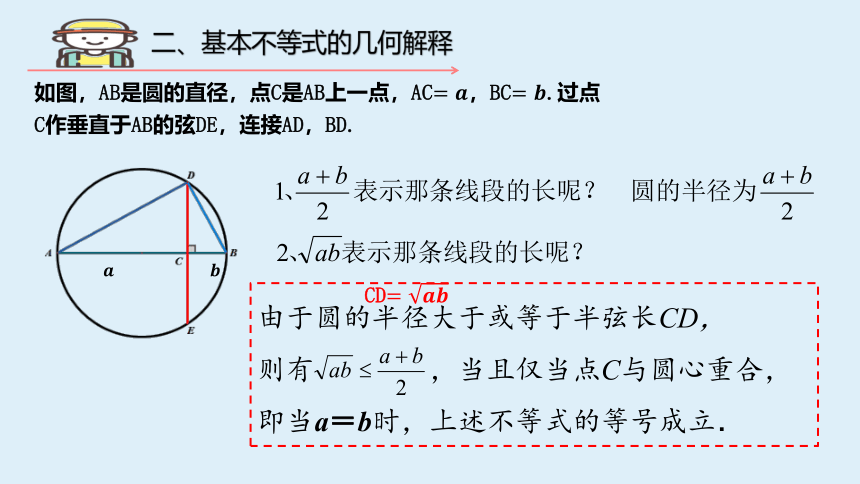
如图,AB是圆的直径,点C是AB上一点,AC=????,BC=????.过点C作垂直于AB的弦DE,连接AD,BD.
?
????
?
????
?
CD=????????
?
由于圆的半径大于或等于半弦长CD,
则有 ,当且仅当点C与圆心重合,
即当a=b时,上述不等式的等号成立.
二、基本不等式的几何解释
三、基本不等式的证明
分析法是一种“执果索因”的证明方法,指从要证的结论出发,逐步寻求使它成立的充分条件,直到归结为判定一个显然成立的条件(已知量、定义、公理、定理、性质、法则等)为止,从而证明论点的正确性、合理性的论证方法。
分析法
⑤
上述证明过程中,每一步推理的依据是什么呢?
二、基本不等式的证明
由于分析法是从要证明的结论出发,逐步寻求使它成立的充分条件,所以分析法在书写过程中必须有相应的文字说明:一般每一步的推理都用“要证……只要证……”的格式,当推导到一个明显成立的条件之后,指出“显然×××成立”.
分析法的证明格式
二、基本不等式的证明
四、学以致用
四、学以致用
解:∵????>????
∴????+????????≥?????????????????=????
当且仅当????=????????,即????=1时,等号成立
∴????+????????的最小值为2.
?
一正
二定
三相等
四、学以致用
1、 已知????>????,则????+????????????的最小值为 .
2、 已知????>????,????>????,且????????=????,则????+????????的最小值为 .
3、 ????+????????的最小值等于 .
?
1、解:∵????>????
∴????+????????????≥?????????????????????=????
当且仅当????=??????????,即????=????????时,等号成立
∴????+????????????的最小值为????.
?
四、学以致用
1、 已知????>????,则????+????????????的最小值为 .
2、 已知????>????,????>????,且????????=????,则????+????????的最小值为 .
3、 ????+????????的最小值等于 .
?
2、解:∵????>????,????>????
∴????+????????≥?????????????????=????
当且仅当????=????????,即????=????,????=????????时,等号成立
∴????+????????的最小值为????.
?
四、学以致用
1、 已知????>????,则????+????????????的最小值为 .
2、 已知????>????,????>????,且????????=????,则????+????????的最小值为 .
3、 ????+????????的最小值等于 .
?
3、解:∵????>????
∴????+????????≥?????????????????=????
当且仅当????=????????,即????=????时,等号成立
∴????+????????的最小值为????.
?
四、学以致用
1、两个不等式
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
重要不等式
基本不等式
形式
适用范围
等号成立的条件
????????+????????≥????????????
?
????????≤????+????????
?
????,????∈????
?
????>????,????>????
?
????=????
?
????=????
?
2、利用基本不等式求最值需要满足三个条件:
一正二定三相等
五、画龙点睛
谢谢大家!
2.2 基本不等式
动手试试看!
先将两张正方形纸沿对角线折成两个等腰直角三角形,再用这两个三角形拼接构造出一个矩形(两边分别等于两个等腰直角三角形的直角边,多余部分折叠)。设这两个正方形的面积分别为a和b,观察两个三角形的面积和矩形面积,你发现了什么?
如果a>0,b>0,我们用 分别代替上式中的a,b,可得到:
由上式可得:
(当且仅当a=b时,等号成立)
? a, b∈R,有a2+b2 ≥ 2ab (当且仅当a=b时,等号成立)
通常称上述不等式为基本不等式.
一、温故知新
正数a,b的算术平均数
正数a,b的几何平均数
基本不等式表明:两个正数的算术平均数不小于它们的几何平均数.
一、温故知新
(当且仅当a=b时,等号成立)
如图,AB是圆的直径,点C是AB上一点,AC=????,BC=????.过点C作垂直于AB的弦DE,连接AD,BD.
?
????
?
????
?
CD=????????
?
由于圆的半径大于或等于半弦长CD,
则有 ,当且仅当点C与圆心重合,
即当a=b时,上述不等式的等号成立.
二、基本不等式的几何解释
三、基本不等式的证明
分析法是一种“执果索因”的证明方法,指从要证的结论出发,逐步寻求使它成立的充分条件,直到归结为判定一个显然成立的条件(已知量、定义、公理、定理、性质、法则等)为止,从而证明论点的正确性、合理性的论证方法。
分析法
⑤
上述证明过程中,每一步推理的依据是什么呢?
二、基本不等式的证明
由于分析法是从要证明的结论出发,逐步寻求使它成立的充分条件,所以分析法在书写过程中必须有相应的文字说明:一般每一步的推理都用“要证……只要证……”的格式,当推导到一个明显成立的条件之后,指出“显然×××成立”.
分析法的证明格式
二、基本不等式的证明
四、学以致用
四、学以致用
解:∵????>????
∴????+????????≥?????????????????=????
当且仅当????=????????,即????=1时,等号成立
∴????+????????的最小值为2.
?
一正
二定
三相等
四、学以致用
1、 已知????>????,则????+????????????的最小值为 .
2、 已知????>????,????>????,且????????=????,则????+????????的最小值为 .
3、 ????+????????的最小值等于 .
?
1、解:∵????>????
∴????+????????????≥?????????????????????=????
当且仅当????=??????????,即????=????????时,等号成立
∴????+????????????的最小值为????.
?
四、学以致用
1、 已知????>????,则????+????????????的最小值为 .
2、 已知????>????,????>????,且????????=????,则????+????????的最小值为 .
3、 ????+????????的最小值等于 .
?
2、解:∵????>????,????>????
∴????+????????≥?????????????????=????
当且仅当????=????????,即????=????,????=????????时,等号成立
∴????+????????的最小值为????.
?
四、学以致用
1、 已知????>????,则????+????????????的最小值为 .
2、 已知????>????,????>????,且????????=????,则????+????????的最小值为 .
3、 ????+????????的最小值等于 .
?
3、解:∵????>????
∴????+????????≥?????????????????=????
当且仅当????=????????,即????=????时,等号成立
∴????+????????的最小值为????.
?
四、学以致用
1、两个不等式
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
重要不等式
基本不等式
形式
适用范围
等号成立的条件
????????+????????≥????????????
?
????????≤????+????????
?
????,????∈????
?
????>????,????>????
?
????=????
?
????=????
?
2、利用基本不等式求最值需要满足三个条件:
一正二定三相等
五、画龙点睛
谢谢大家!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
